SE-Modeling-NP-3-3-17.Pdf
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mysuru Bar Association : Mysuru Taluk : Mysuru District : Mysuru
3/17/2018 KARNATAKA STATE BAR COUNCIL, OLD KGID BUILDING, BENGALURU VOTER LIST POLING BOOTH/PLACE OF VOTING : MYSURU BAR ASSOCIATION : MYSURU TALUK : MYSURU DISTRICT : MYSURU SL.NO. NAME SIGNATURE BYRAPPA S MYS/15/55 S/O SIDDIAH 1 D NO.3108/B 4TH CROSS VIVEKANAND ROAD YADAVAGIRI EXTN MYSURU MYSURU 20 CHANDRASEKHAR H N MYS/30/59 S/O 2 1065 JAYA LAKSHMI VILAS ROAD CHAMARAJA PURAM . MYSURU MYSURU 570 005 GANGADHARAN H MYS/36/59 S/O RUDRAPPA 3 1089 VISHNUVARDHAN ROAD CHAMARAJAPURAM MYSURU MYSURU 570005 KANTHARAJA SETTY K V MYS/484/62 4 S/O KRISHNA SHETTY K V L-26 1ST STAGE KUVEMPU NAGAR MYSURU MYSURU 570 023 1/320 3/17/2018 KRISHNA IYENGAR M S MYS/690/62 S/O M V KRISHNA IYENGAR 5 NO.1296 IV TH WEST CROSS 3RD MAIN ROAD KRISHNAMURTHYPURAM MYSURU MYSURU 04 SHIVASWAMY S A MYS/126/63 6 S/O APPAJIGOWDA SARASWATHIPURAM MYSURU MYSURU THONTADARYA MYS/81/68 S/O B.S. SIDDALINGASETTY 7 B.L 208 12TH MAIN 3RD CROSS SARASWATHIPURAM MYSURU MYSURU 570009 SRINIVASAN RANGA SWAMY MYS/190/68 S/O V R RANGASWAMY IGENGAL 8 416 VEENE SHAMANNA'S STREET OLD AGRAHARA MYSURU MYSURU 570 004 SESHU YEDATORE GUNDU RAO MYS/278/68 9 S/O Y.V.GUNDURAO YEDATORE 447/A-4 1 ST CROSS JAYA LAXMI VILAS ROAD MYSURU MYSURU 570 005 2/320 3/17/2018 RAMESH HAMPAPURA RANGA SWAMY MYS/314/68 S/O H.S. RANGA SWAMY 10 NO.27 14TH BLOCK SBM COLONY SRIRAMPURA 2ND STAGE MYSURU MYSURU 570023 ASWATHA NARAYANA RAO SHAM RAO MYS/351/68 11 S/O M.SHAMARAO 1396 D BLOCK KUVEMPUNAGAR MYSURU MYSURU 570023 SREENIVASA NATANAHALLY THIMME GOWDA MYS/133/69 S/O THIMMEGOWDA 12 NO 22 JAYASHREE NILAYA 12TH CROSS V.V.MOHALLA MYSURU MYSURU 2 DASE GOWDA SINGE GOWDA MYS/255/69 13 S/O SINGE GOWDA NO. -

District Census Handbook, Mandya, Part X-A, B, Series-14,Mysore
CENSUS OF INDIA 1971 S E R I E S-14 MYSORE DISTRICT CENSUS HANDBOOK MANDYA DISTRICT PART X-A: TOWN AND VILLAGE DIRECTORY PART X-B: PRIMARY CENSUS ABSTRACT P. PAD MAN A B H A OF THE INDIAN ADMINISTRATIVE SERVICE DIRECTOR OF CENSUS OPERATIONS MYSORE 24 12 0 24 ... 72 MILES m1f~CD)U -·!~.r-~=.~~~~!~~==~!;;If"!~ : iii: 20 0 20 40 60 eo 100 klt.OM£TRES ADMINISTRATIVE DIVISIONS, 1971 STA TE BOUNDARY DISTRICT " TALUk " STATE CAPITAL * OISTRICT HEADQUARTERS @ TALUk o T. Naulput - ThirumaI<udIu Naulpur Ho-Hoopct H-HubU ANDHRA PRADESH CHELUVANARA YANA TEMPLE, MELKOTE (Mot{f on the cover) The illustration on the cover page represents the temple dedicated to Krishna as CheluVG Pulle-Raya at Melkote town in Mandya district. The temple is a square building of great dimensions but very plain in design. The original name of the principal deity is said to .have been Rama Priya. According to tradition, Lord Narayana of Melkote appeared in a dream to Sri Ramanuja (the 12th century Vaishnava Saint and propounder of the philosophy of Visishtadvait(!) and said to him that He was awaiting him on Yadugiri Hill. Thereupon, v,:ith the assistance of .Hoysala King Vishnu vardhana (who had received tapta-mudra from Ramanuja and embraced Vaishnavism) he discovered the idol which lay covered by an ant-hill which he excavated and worshipped. This incident is said to have occurred in the month of Tai in Bahudharaya year. A temple \.vas erected for Lord Narayana over the ant-hill and the installation of tlle image took place in 1100 A.D. -

District Census Handbook, Mandya, Part XII-B, Series-11
CENSUS OF INDIA 1991 Serit'~ - II KARNATAKA DISTRICT CENSUS HANDBOOK MANDYA DISTRICT PART XII - B VILLAGE AND TOWN WISE PRIMARY CENSUS ABSTRACT "\OBII \ N-\l\1BISr\N Din'dor of Cl'lI~lI~ Opl'ralioll!<., Ka"lIalaka 77' KARNATAKA ADMINISTRA TIVE DIVISIONS 1991 leO Ie' Where the name of the district I taluk differs from that of its headquarters town name the former appears within brackets. ARABIAN 5£A Bansalore is the headquarters for 8angalore North und Bangalore South taluks lind also (or BlfnBlllore lind BlIngliJore Rurlll Districts. T·Tumkur o 13. " .. BOUNDARIES :- STATE .. DISTRICT. TALUK .. HEADQUARTERS :- 12 STATE .. DISTRICT. @ TALUK .. *o K1LOMETRES 60 :zp 'PY )0 4f I 74° East of Greenwict'l 77' Based upon Survey of Indio map with the permission of the S.rveyor General 0 f India. © Government of Indio Copyright, 1994. The terrilorlal water. of Indio ••tend into lhe sea to a distonce of lwelve naulical miles mellSured from the appropriate bose lin •. CONTENTS F< m.EWORD \ 1 PREF/\('E \'11 \,111 1)\11'( mTANT STATISTICS 1:1. - Xli ,\i'\ALYTICAL NOTE .:',"\ PRL\IARY (_'ENSLI~ ABSTRACT E\pl.lIlalory Nolc~ 31 - 34 A. Dj~l riel Primary Ce 11~1l" Ah~l ract 3(1 - .+7 {i) Villagc.Tll\\n Priman ('cn~lI~ Ah~tr,lct /\lph;thetical Li~( llJ VilLtge:-, Kri"hn;1I ;Ijpcl CD. Billd, 51 ."i:-: Prinldn l'ell:-'ll~ />..h-'(I ael 1...:.1 i"hnarailll'l (·.f).Rlnd (.1) ()() Alph<thetical Li:-,( oj Village~ - i\laddur C.D.Blnd, 10., 11)7 Primary Cen"u'-. Ah"tract - l\laddur C.D.Block I()~ - 1.:'7 Alphahetical Li:-,( of Village:-, l\Lt1a\ alii CD.Block 131 - 1.1,5 Primary ('en:-L1:- Ah:-.lract - l\1ala\alli CD.B1ock 1.1,() - 15') t\lphahetical Li:-,( of Villa!!e~ - I\lall((\'a ('.D.Block Ih.~ - HI7 Primary (\;n~L1" Ab"tral·t ;VLtndya (',D.BI(iCk 1(,1' II) I Alphabetical Li:-t of Village~ N;tg;lInang;lla CD. -

0 0 23 Feb 2021 152000417
Annexure I Annexure II ' .!'r ' .tu." "ffi* Government of Maharashtra, Directorate of Geology and Mining, "Khanij Bhavan",27, Shivaji Nagar, Cement Road, Nagpur-,1.10010 CERTIFICATE This is hereby certified that the mining lease granted to ]Ws Minerals & Metals over an area 27.45.20 Hec. situated in village Redi, Taluka Vengurla, District- Sindhudurg has no production of mineral since its originally lease deed execution. This certificate is issued on the basis of data provided by the District Collectorate, Sindhudurg. Mr*t, Place - Nagpur Director, Date - l1109/2020 Directorate of Geology and Mining, Government of Maharashtra, Nagpur 'ffi & r6nrr arn;r \k{rc sTrnrr qfrT6{ rtqailEc, ttufrg Qs, rr+at', fula rl-c, ffi qm, - YXo oqo ({lrr{ fF. osRe-?eao\e\\ t-m f. oeit-tlqqeqr f-+d , [email protected], [email protected]!.in *-.(rffi rw+m-12,S-s{r.r- x/?ol./ 26 5 5 flfii6- tocteo?o yfr, ll lsepzolo ifuflRirrs+ew, I J 1r.3TrvfdNfu{-{r rrs. \ffi-xooolq fus-q ti.H m.ffi, tu.frgq,l ffi ql* 1s.yr t ffiTq sF<-qrartq-qrsrufl -srd-d.. vs1{ cl fu€I EFro.{ srfffi, feqi,t fi q* fr.qo7o1,7qoqo. rl enqd qx fl<ato lq/os/?o?o Bq-tn Bqqri' gr{d,rr+ f frflw oTu-s +.€, r}.t* ar.ffi, fii.fufli ++d sll tir.xq t E'fr-qrqr T6 c$ Efurqgr tTer<ir+ RctsTcr{r :-err+ grd ;RrerrqTEkT squrq-d qT€t{d df,r{ +'t"qra *a eG. Tr6qrl :- irftf,fclo} In@r- t qr.{qrroi* qrqi;dqrf,q I fc.vfi.firqr|. -

Government of Karnataka Provisional Habitation Wise Neighbourhood
Government of Karnataka O/o Commissioner for Public Instruction, Nrupatunga Road, Bangalore - 560001 RURAL Provisional Habitation wise Neighbourhood Schools - 2016 ( RURAL ) Habitation Name School Code Management Lowest Highest Entry type class class class Habitation code / Ward code School Name Medium Sl.No. District : Mandya Block : KRISHNARAJA PET Habitation : ACHHAMANA HALLY---29220100101 29220100101 29220100101 Govt. 1 5 Class 1 ACHHAMANA HALLY GLPS ACHAMANA HALLY 05 - Kannada 1 Habitation : ADDIHALLY---29220100201 29220100201 29220100201 Govt. 1 5 Class 1 ADDIHALLY GLPS ADI HALLY 05 - Kannada 2 Habitation : AGASARAHALLY---29220100301 29220100301 29220100301 Govt. 1 7 Class 1 AGASARAHALLY GHPS AGASARA HALLY 05 - Kannada 3 Habitation : AGAHALAYA---29220100501 29220100501 29220100501 Govt. 1 7 Class 1 AGAHALAYA GHPS AGHALAYA 05 - Kannada 4 29220100501 29220100503 Pvt Unaided 1 7 Class 1 AGAHALAYA POORNAPRAJNA AGHALAYA 05 - Kannada 5 Habitation : AGRAHARABACHAHALLY---29220100601 29220100601 29220100601 Govt. 1 7 Class 1 AGRAHARABACHAHALLY GHPS AGRAHARA BACHA HALLY 05 - Kannada 6 Habitation : AKKIHEBALLU---29220100701 29220100701 29220100701 Govt. 1 7 Class 1 AKKIHEBALLU GHPS AKKI HEBBALU 05 - Kannada 7 29220100701 29220100702 Govt. 1 7 Class 1 AKKIHEBALLU GHP URDU SCHOOL AKKI HEBBALU 18 - Urdu 8 29220100701 29220100703 Pvt Unaided 1 10 Class 1 AKKIHEBALLU POORNA CHANDRA HPS AKKIHEBBALU 05 - Kannada 9 29220100701 29220100707 Pvt Unaided 1 5 LKG AKKIHEBALLU S.K.I. EDUCATION TRUST AKKIHEBBALU 19 - English 10 Habitation : ALAMBADIKAVALU---29220100801 -
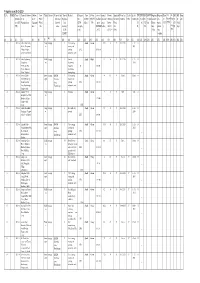
Kodagu Updated F-Register As on 31-03-2019
F-Register as on 31-03-2019 Sl.No. PCBID Year of Name & Address Address Area/ Taluk District Name of the Type of Product Category Size Colour date of capital Present Applicabi Water Act Air Act Air Act HW HWM BM BMW Registrati Registrat Batte E- E- MS MS Rem Identifica of the of the Place/ Industrial Organisat No (L/M/S/ (R/O/G/ establish investme Working lity under (Validity) (Y/N) (Validity M (Validi W (Valid on under ion ry Waste Wast W W arks tion (YY- Organisations Organisat Ward Estates/ ion/ (XGN Micro) W) ment nt (in Status Water ) (Y/ ty) (Y/ ity) Plastic under (Y/N (Y/N) e (Y/ (Vali YY) ions No. areas Activity* category (DD/MM Lakhs) (O/C1/ Act N) N) rules plastic ) (Vali N) dity) (I/ M/ code) /YY) C2/Y)** (Y/N) (Y/N) rules dity) LB/HC/ (validity (8) H/L/CE/ date) (1) (2) (3) (4) (5) (6) (7) (9) (10) (11) (12) (13) (14) (15) (16) (17) (18) (19) (20) (21) (22) (23) (24) (25) (26) (27) (28) (29) (30) (31) (32) (33) 1 2013-14 A.R. Coffee Curing Virajp Kodagu I Coffee curing, Small Green 13.65 O Y 31-12-2021 31-12- N Works, Halagunda et roasting and 2021 Village, Virajpet grinding 1572 30/11/1999 _ taluk, Coorg District. (industrial scale) 2 2013-14 Abrar Engineering Madik Kodagu I General Small White 3.5 O Y 31-12-2114 31-12- N Corporation, eri Engineering 2114 P.B.No.46, Plot Industries 14 25/9/2001 _ No.L4, Industrial (Excluding Estate, Madikeri, electroplating, 3 2013-14 Aimara Coffee Somw Kodagu KIADB I Coffee curing, Small Green 48 C1 Y Closed Closed N Curing Works, 1p, arpet Industrial roasting and Kiadb Industrial Area, grinding 1572 23/7/1999 _ Area, Kushalnagar, Kushalnagar (industrial scale) Virajpet taluk, 4 2013-14 Akshara Wood Virajp Kodagu I Saw mills Small Green 5 Y Y YTC YTC N Industries, No.89/11, et Mathoon Village, 11/7/2002 _ Virajpet taluk, Coorg. -

Programme Study Centre (Pscs) Wise Allocation of Bsc Nursing Graduate Candidates for IGNOU- CCHN Training
Programme Study Centre (PSCs) wise Allocation of BSc Nursing Graduate Candidates for IGNOU- CCHN training. (Candidates shall report directly to Programme Incharge (PIC) of PSCs on 16-9-2020; Note:- common relieving letter shall be sent from districts to concerned PICs of PSCs) Name of Programme Study Center (PSC) K C General Hospital, Malleshwaram, Bengaluru Sl No Candidate Name DOB Address Name of District 1 KIRAN 16/05/1993 #2061/68 BEHIND SAPTHAGIRI SCHOOL CHIGATERI LAYOUT DAVANAGERE U Kannada 2 RAKESH S 25/12/1995 BORAGUNTE. BADAVANAHALLI (POST). MADHUGIRI (T). TUMKUR (D 572112 U Kannada 3 Banuprakash R 02/03/1989 48 sangahalli road belalagere channagiri U Kannada 4 ASHA K G 08/01/1983 KHUSHI MEDICARE HEMAVATHI NAGAR MAIN ROAD HASSAN U Kannada 5 RANJITHKUMAR S V 05/04/1994 SIRESANDRA VILLAGE SHAPUR POST KOLAR TALUK KOLAR DIST U Kannada 6 USHA RANI H C 30/12/1996 hosathimmappanahatti nagathihalli post mathodu hobli hosadurga taluk U Kannada 7 VIJAY KUMAR C 04/12/1994 S/O CHANDRAPPA VANARASI ( V ) MUDUVADI ( P ) KOLAR ( T ) & ( D )-563101 U Kannada 8 ASHA GAVADI 14/10/1992 AT BARGI PO BARGI TQ KUMTA DIS UTTAR KANNADA 581440 U Kannada 9 KENAZ N SAMUEL 09/06/1996 NEAR CHOWDESHWARI TEMPLE BEHIND A P M C YARD BATAWADI KYATHASAND U Kannada 10 SIDDESH S 15/05/1995 KENGAPURA V, KANIVEBILICHI P, CHANNAGIRI TQ DAVANAGERE 577231 U Kannada 11 GAYATRI 01/04/1984 #119 Krishna Nagar , 2nd Cross ,SIT Extension , Kuvempunagar Tumakuru U Kannada 12 RAKESH K R 13.05.1996 S/O Rajappa K V Kagathuru post Channagiri Tq Davanagere Dist 577221 Chitradurga -

Kodagu District Disaster Management Plan 2017-18
Kodagu District Disaster Management Plan 2017-18 Kodagu District Disaster Management Plan 2017-18 Kodagu District map Message (Deputy Commissioner) Kodagu District Disaster Management Plan 2017-18 Index Content Page No. Abbreviation 1 Kodagu District Disaster Management Team 2-4 Chapter-1 INTRODUCTION 5-14 PART – A 1. DISTRICT PROFILE 1.1 Geography 1.2 Rainfall And Climate 1.3 Demography Of The Land 1.4 Kodagu District Administrative Setup 1.5 Socio Economic Profile Of The District 1.6.A. Agriculture 1.6.B. Geo Morphology Of Soil Types 1.6.C. Education 1.6.D. Tourism 1.6.E. Land Utilization Details 1.6.F. Infrastructure 1.6.G. Critical Infrastructures Of The District PART- B 15-18 1.7 Key Resources Of The Kodagu District 1.7a Details Of Rivers And Dams 1.7b Details Of Drinking Water 1.7c Flora And Fauna 1.8 Road Network 1.9 Details Of Media And Communications 1.10. Details of Power Generating Industries 1.11 Details Of Industries PART-C 19-26 1.12 Kodagu District Disaster Management Plan 1.12. A Scope Of The Kodagu District Disaster Management Plan: 1.12. B Kodagu - District Disaster Management Authority (DDMA):- 1.12.C. Laws And Statues 1.12.D Powers And Functions Of Kodagu District Authority 1.12.E The Plan development 1.13 Stake Holders And Their Responsibility 1.14 Kodagu ULBs And Their Support For Dm Plan 1.15. Formal Agreement (MOU) With Utility Agencies Kodagu District Disaster Management Plan 2017-18 1.16 How To Use The DDMP Plan 1.17 Approval Mechanism Of The DDMP – Authority For Implementation (State Level/District Level Orders) -

2922 Part B Dchb Kodagu
Census of India 2011 KARNATAKA PART XII-B SERIES-30 DISTRICT CENSUS HANDBOOK KODAGU VILLAGE AND TOWN WISE PRIMARY CENSUS ABSTRACT (PCA) DIRECTORATE OF CENSUS OPERATIONS KARNATAKA © Government of India copyright, 2014. The maps included in this publication are under © Government of India copyright, 2014. The responsibility for the correctness of internal details rests with the publisher. The territorial water of India extend into the sea to a distance of twelve nautical miles measured from the appropriate base line. The external boundaries and coastlines of India agree with the Record/Master Copy certified by Survey of India. CENSUS OF INDIA 2011 KARNATAKA SERIES-30 PART XII-B DISTRICT CENSUS HANDBOOK KODAGU VILLAGE AND TOWN WISE PRIMARY CENSUS ABSTRACT (PCA) Directorate of Census Operations, KARNATAKA MOTIF RAJA'S SEAT, MADIKERI Raja's Seat (Seat of the King) is a seasonal garden of flowers and artificial fountains. It is one of the most important tourist spots in Madikeri town of Kodagu district. Madikeri also known as Mercara was founded by a prince Muddu Raja of the Haleri dynasty in 1681 A.D. Raja's seat is an elevated spot overlooking a vast greenery. This spot was frequented by the royalty with a view to enjoy the scenic beauty of the valleys. It commands a thrilling view of the surrounding area. Standing in the open, the seat is provided with heavy masonry arched pavilion from where the visitor can see one of the finest and most enchanting views. Source-Archaeological Survey of India Contents Pages 1 Foreword 1 2 Preface 3 3 Acknowledgement -

Sub Centre List As Per HMIS SR
Sub Centre list as per HMIS SR. DISTRICT NAME SUB DISTRICT FACILITY NAME NO. 1 Bagalkote Badami ADAGAL 2 Bagalkote Badami AGASANAKOPPA 3 Bagalkote Badami ANAVALA 4 Bagalkote Badami BELUR 5 Bagalkote Badami CHOLACHAGUDDA 6 Bagalkote Badami GOVANAKOPPA 7 Bagalkote Badami HALADURA 8 Bagalkote Badami HALAKURKI 9 Bagalkote Badami HALIGERI 10 Bagalkote Badami HANAPUR SP 11 Bagalkote Badami HANGARAGI 12 Bagalkote Badami HANSANUR 13 Bagalkote Badami HEBBALLI 14 Bagalkote Badami HOOLAGERI 15 Bagalkote Badami HOSAKOTI 16 Bagalkote Badami HOSUR 17 Bagalkote Badami JALAGERI 18 Bagalkote Badami JALIHALA 19 Bagalkote Badami KAGALGOMBA 20 Bagalkote Badami KAKNUR 21 Bagalkote Badami KARADIGUDDA 22 Bagalkote Badami KATAGERI 23 Bagalkote Badami KATARAKI 24 Bagalkote Badami KELAVADI 25 Bagalkote Badami KERUR-A 26 Bagalkote Badami KERUR-B 27 Bagalkote Badami KOTIKAL 28 Bagalkote Badami KULAGERICROSS 29 Bagalkote Badami KUTAKANAKERI 30 Bagalkote Badami LAYADAGUNDI 31 Bagalkote Badami MAMATGERI 32 Bagalkote Badami MUSTIGERI 33 Bagalkote Badami MUTTALAGERI 34 Bagalkote Badami NANDIKESHWAR 35 Bagalkote Badami NARASAPURA 36 Bagalkote Badami NILAGUND 37 Bagalkote Badami NIRALAKERI 38 Bagalkote Badami PATTADKALL - A 39 Bagalkote Badami PATTADKALL - B 40 Bagalkote Badami SHIRABADAGI 41 Bagalkote Badami SULLA 42 Bagalkote Badami TOGUNSHI 43 Bagalkote Badami YANDIGERI 44 Bagalkote Badami YANKANCHI 45 Bagalkote Badami YARGOPPA SB 46 Bagalkote Bagalkot BENAKATTI 47 Bagalkote Bagalkot BENNUR Sub Centre list as per HMIS SR. DISTRICT NAME SUB DISTRICT FACILITY NAME NO. -

2007-08 40 (Ii) Explanatory Notes 43 No
GOVERNMENT OF KARNATAKA FINANCE ACCOUNTS 2007-2008 TABLE OF CONTENTS Reference to page Certificate of the Comptroller and Auditor General of India 3 Introductory 4 PART 1 - SUMMARISED STATEMENTS No. 1 - Summary of Transactions 8 - Explanatory Notes 20 No. 2 - Capital Outlay outside the Revenue Account (i) Progressive Capital Outlay to end of 2007-08 40 (ii) Explanatory Notes 43 No. 3 - (i) Financial results of Irrigation Works 46 (ii) Financial results of Electricity Schemes 47 No. 4 - Debt Position - (i) Statement of Borrowings 48 (ii) Other Obligations 50 (iii) Service of Debt 51 No. 5 - Loans and Advances by State Government - (i) Statement of Loans and Advances 52 (ii) Recoveries in arrears 53 No. 6 - Guarantees given by the Government of Karnataka in respect of loans etc., raised by Statutory Corporations, Government Companies, Local Bodies and other Institutions 56 No. 7 - Cash balances and investments of cash balances 62 No. 8 - Summary of balances under Consolidated Fund, Contingency Fund and Public Account 64 PART II - DETAILED ACCOUNTS AND OTHER STATEMENTS SECTION A - REVENUE AND EXPENDITURE No. 9 - Statement of revenue and expenditure for the year 2007-08 expressed as a percentage of total revenue / total expenditure 71 No. 10 - Statement showing the distribution between charged and voted expenditure 74 No. 11 - Detailed account of revenue receipts and capital receipts by minor heads 75 No. 12 - Detailed account of expenditure by minor heads 95 No. 13 - Detailed statement of capital expenditure during and to end of the year 2007-08 132 No. 14 - Details of investments of Government in Statutory Corporations, Government Companies, Other Joint Stock companies, Co-operative Banks and Societies etc., to end of 2007-08 251 No. -

Government of Karnataka List of Minority Schools
Government of Karnataka O/o Commissioner for Public Instruction, Nrupatunga Road, Bangalore - 560001 List of Minority Schools - 2015 Habitation Name School Code Management Lowest High Entry type class class class Habitation code / Ward code School Name Medium Sl.No. District : Mandya Block : MALAVALLY 29220305201 29220305202 Pvt Unaided 1 5 Class 1 GOLLARA HALLY LPS DIVYAJYOTHI CONVENT 05 - Kannada 1 29220318801 29220318801 Pvt Unaided 1 8 Class 1 MALAVALLY - WARD-3 ANITA HPS MALAVALLY 19 - English 2 29220319601 29220319601 Pvt Aided 1 7 LKG MALAVALLY - WARD-11 MISSION AIDED HPS MALAVALLY 05 - Kannada 3 29220319701 29220319703 Pvt Unaided 1 7 Class 1 MALAVALLY - WARD-12 ALAMEEN SS MALAVALLY 05 - Kannada 4 Deputy Director Chief Executive Officer DEPARTMENT OF PUBLIC INSTRUCTION ZILLA PANCHAYATH e-Governance, CPI office, Bangalore 12/18/2014 -11:54:28 AM 1 Government of Karnataka O/o Commissioner for Public Instruction, Nrupatunga Road, Bangalore - 560001 Revenue village, Habitation wise Aided and UnAided Neighbourhood Schools - 2015 RURAL Habitation Name School Code Management Lowest High Entry type class class class Habitation code / Ward code School Name Medium Sl.No. District : Mandya Block : MALAVALLY Revenue Village : 29220315306 Pvt Unaided 1 3 LKG POORNA PRAJNA LPS 05 - Kannada 1 29220307708 Pvt Unaided 1 5 LKG SPANDANA PUBLIC SCHOOL HUSKUR 05 - Kannada 2 Revenue Village : B. G. PURA 29220301101 29220301103 Pvt Unaided 1 7 LKG B.G.PURA KARIBASAVESWARA HPS B.G.PURA 05 - Kannada 3 Revenue Village : BACHANA HALLY 29220301201 29220301202