DOCSLIB.ORG

Measuring Uncertainty of Protein Secondary Structure

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Measuring Uncertainty of Protein Secondary Structure Wright State University CORE Scholar Browse all Theses and Dissertations Theses and Dissertations 2011 Measuring Uncertainty of Protein Secondary Structure Alan Eugene Herner Wright State University Follow this and additional works at: https://corescholar.libraries.wright.edu/etd_all Part of the Computer Engineering Commons, and the Computer Sciences Commons Repository Citation Herner, Alan Eugene, "Measuring Uncertainty of Protein Secondary Structure" (2011). Browse all Theses and Dissertations. 422. https://corescholar.libraries.wright.edu/etd_all/422 This Dissertation is brought to you for free and open access by the Theses and Dissertations at CORE Scholar. It has been accepted for inclusion in Browse all Theses and Dissertations by an authorized administrator of CORE Scholar. For more information, please contact [email protected]. MEASURING UNCERTAINTY OF PROTEIN SECONDARY STRUCTURE A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy By Alan Eugene Herner B.A. Wright State University, 1980 M.S. Wright State University, 1980 M.S. Wright State University, 2001 _____________________________________________ 2011 Wright State University COPYRIGHT BY Alan E. Herner 2011 WRIGHT STATE UNIVERSITY SCHOOL OF GRADUATE STUDIES January 7, 2011 I HEREBY RECOMMEND THAT THE DISSERTATION PREPARED UNDER MY SUPERVISION BY ALAN E. HERNER ENTITLED Measuring Uncertainty of Protein Secondary Structure BE ACCEPTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY. ________________________ Michael L. Raymer, PhD Dissertation Director ________________________ Arthur A. Goshtasby, PhD Director, Computer Science and Engineering PhD Program ________________________ Andrew Hsu, PhD Dean School of Graduate Studies Committee Final Examination ____________________ Michael L. Raymer, PhD ____________________ Gerald Alter, PhD ____________________ Travis Doom, PhD ____________________ Ruth Pachter, PhD _____________________ Mateen Rizki, PhD ABSTRACT Herner, Alan E. PhD. Department of Computer Science and Engineering, Wright State University, 2011. Measuring Uncertainty of Protein Secondary Structure. This dissertation develops and demonstrates a method to measure the uncertainty of secondary structure of protein sequences using Shannon’s information theory. This method is applied to a newly developed large dataset of chameleon sequences and to several protein hinges culled from the Hinge Atlas. The uncertainty of the central residue in each tripeptide is computed for each amino acid in a sequence using Cuff and Barton’s CB513 as the reference set. It is shown that while secondary structure uncertainty is relatively high in chameleon regions [avg = 1.27 bits] it is relatively low in the regions 1- 7 residues nearest a chameleon [N terminus flank avg = 1.12 bits; C terminus flank avg = 1.16 bits]. This difference is shown to be highly statistically significant [ p = 9.6E-18 and p = 2.9E-12, respectively]. It is also shown that the secondary structure uncertainty of hinge regions was not found to be different to a statistically significant degree once a Bonferroni multiple test correction was applied. A new hand curated database of long “chameleon” sequences was developed. It contains nine sequences of length eight and eighty-five sequences of length seven. iv TABLE OF CONTENTS 1.0 INTRODUCTION .........................................................................................................1 1.1 Overview ........................................................................................................................1 1.1.1 Research Objective and Significance ...................................................................3 1.1.2 Organization of the Report ...................................................................................4 1.2 Proteins ..........................................................................................................................5 1.2.1 Amino acid composition and peptide bonds ........................................................5 1.2.2 Types of Amino Acids .........................................................................................7 1.2.3 Planarity and Dihedral angles ..............................................................................7 1.2.4 Conformational Constraints .................................................................................8 1.2.5 Molecular forces involved in protein folding .......................................................9 1.2.5.1 Hydrogen bonds ...........................................................................................10 1.2.5.3 Ionic (charge) interactions ...........................................................................11 1.2.5.4 Covalent bonds.............................................................................................12 1.2.5.5 Van der Waals forces ...................................................................................13 1.2.6 Protein Structure .................................................................................................13 1.2.6.1 Primary Structure .........................................................................................13 1.2.6.2 Secondary Structure .....................................................................................14 1.2.6.2.1 Alpha Helix............................................................................................14 1.2.6.2.2 Extended strand .....................................................................................15 1.2.6.2.3 Random Coil ..........................................................................................16 1.2.6.3 Motifs ...........................................................................................................17 1.2.6.4 Tertiary Structure .........................................................................................17 1.2.6.5 Quaternary Structure ....................................................................................18 1.2.7 Theories of Folding ............................................................................................19 1.2.7.1 Framework Model ........................................................................................19 1.2.7.2 Hydrophobic Collapse Model ......................................................................19 1.2.7.3 Nucleation Model.........................................................................................20 1.2.7.4 Unified Model ..............................................................................................20 1.3 Protein Data and Databases .........................................................................................21 1.3.1 Experimental data ...............................................................................................21 1.3.1.1 X-ray crystallography ..................................................................................21 1.3.1.2 Nuclear Magnetic Resonance (NMR) .........................................................22 v 1.3.2 Dictionary of Secondary Structure of Proteins (DSSP) ....................................23 1.3.3 Data sets .............................................................................................................24 1.3.3.1 Redundancy and Homology .........................................................................24 1.3.3.2 Data Sources ................................................................................................26 1.3.3.2.1 wwProtein Data Bank (PDB) ................................................................26 1.3.3.2.2 Customized Data Sets ............................................................................27 1.3.3.3 Data Formats ................................................................................................28 1.3.3.3.1 FASTA...................................................................................................28 1.3.3.3.2 Protein Data Bank ..................................................................................29 1.3.4 Eight to three reduction ......................................................................................29 2.0 LITERATURE REVIEW ............................................................................................31 2.1 Secondary Structure Prediction....................................................................................31 2.1.1 Foundations ........................................................................................................31 2.1.1.1 Early Investigations .....................................................................................31 2.1.1.2 Thermodynamic Hypothesis ........................................................................32 2.1.1.3 Levinthal’s Paradox .....................................................................................33 2.1.2 Illustrative Papers ...............................................................................................34 2.1.2.1 Physico-chemical .........................................................................................34 2.1.2.1.1 Helical wheels ........................................................................................34 2.1.2.1.2 Physical rules .........................................................................................35 2.1.2.1.3 Molecular Dynamics ..............................................................................35 2.1.2.2 Statistical
Load more

Recommended publications
  • The TIM Barrel Fold Nagarajan D
    The TIM barrel fold Nagarajan D. and Nanajkar N. Comments and corrections: Line 10: fix “αhelices” in “α-helices”. Lines 11-12: C-terminal loops are important for catalytic activity, while N-terminal loops are important for the stability of the TIM-barrels. This should be mentioned. Line 14: The reference #7 is not related to the statement. Line 14: There is a new EC classe (EC.7, translocases). Change “5 of 6” in “5 of 7”. Lines 26-27: It is not correct to state that the shear number of 8 for the TIM-barrels is due to “their staggered nature”. Most of the β-barrels have a staggered nature, but their shear number is not 8. Line 27: The reference #2 is imprecise. Wierenga did not defined himself the shear number of TIM-barrel proteins. Please check the 2 papers of Murzin AG, 1994, “Principle determining the structure of β-sheet barrels in proteins,” I and II, and the paper of Liu W, 1998, “Shear numbers of protein β-barrels: definition refinements and statistics”. Line 29: Again, it is not correct to state that the 4-fold geometric symmetry depends on the stagger. Since the number of strands (n) is equal to the Shear number (S), side-chains point alternatively towards the pore and the core, giving a 4-fold symmetry. Line 37: “historically” is a bit exaggerated for a reference dated 2015, especially if it comes from the author itself. Find a true historic reference, or just mention that you defined the regions “core” and “pore”. Line 43: “Consequently” is misleading.
    [Show full text]
  • Smurflite: Combining Simplified Markov Random Fields With
    SMURFLite: combining simplified Markov random fields with simulated evolution improves remote homology detection for beta-structural proteins into the twilight zone Noah M. Daniels 1, Raghavendra Hosur 2, Bonnie Berger 2∗, and Lenore J. Cowen 1∗ 1Department of Computer Science, Tufts University, Medford, MA 02155 2Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology, Cambridge, MA 02139 ABSTRACT are limited in their power to recognize remote homologs because of Motivation: One of the most successful methods to date for their inability to model statistical dependencies between amino-acid recognizing protein sequences that are evolutionarily related has residues that are close in space but far apart in sequence (Lifson and been profile Hidden Markov Models (HMMs). However, these models Sander (1980); Zhu and Braun (1999); Olmea et al. (1999); Cowen do not capture pairwise statistical preferences of residues that are et al. (2002); Steward and Thorton (2002)). hydrogen bonded in beta sheets. These dependencies have been For this reason, many have suggested (White et al. (1994); partially captured in the HMM setting by simulated evolution in the Lathrop and Smith (1996); Thomas et al. (2008); Liu et al. (2009); training phase and can be fully captured by Markov Random Fields Menke et al. (2010); Peng and Xu (2011)) that more powerful (MRFs). However, the MRFs can be computationally prohibitive when Markov Random Fields (MRFs) be used. MRFs employ an auxiliary beta strands are interleaved in complex topologies. dependency graph which allows them to model more complex We introduce SMURFLite, a method that combines both simplified statistical dependencies, including statistical dependencies that Markov Random Fields and simulated evolution to substantially occur between amino-acid residues that are hydrogen bonded in beta improve remote homology detection for beta structures.
    [Show full text]
  • Mechanism of Resilin Elasticity
    ARTICLE Received 24 Oct 2011 | Accepted 11 Jul 2012 | Published 14 Aug 2012 DOI: 10.1038/ncomms2004 Mechanism of resilin elasticity Guokui Qin1,*, Xiao Hu1,*, Peggy Cebe2 & David L. Kaplan1 Resilin is critical in the flight and jumping systems of insects as a polymeric rubber-like protein with outstanding elasticity. However, insight into the underlying molecular mechanisms responsible for resilin elasticity remains undefined. Here we report the structure and function of resilin from Drosophila CG15920. A reversible beta-turn transition was identified in the peptide encoded by exon III and for full-length resilin during energy input and release, features that correlate to the rapid deformation of resilin during functions in vivo. Micellar structures and nanoporous patterns formed after beta-turn structures were present via changes in either the thermal or the mechanical inputs. A model is proposed to explain the super elasticity and energy conversion mechanisms of resilin, providing important insight into structure–function relationships for this protein. Furthermore, this model offers a view of elastomeric proteins in general where beta-turn-related structures serve as fundamental units of the structure and elasticity. 1 Department of Biomedical Engineering, Tufts University, Medford, Massachusetts 02155, USA. 2 Department of Physics and Astronomy, Tufts University, Medford, Massachusetts 02155, USA. *These authors contributed equally to this work. Correspondence and requests for materials should be addressed to D.L.K. (email: [email protected]).
    [Show full text]
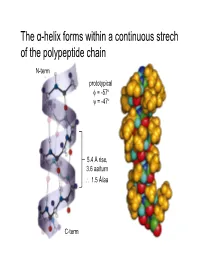
  • The Α-Helix Forms Within a Continuous Strech of the Polypeptide Chain
    The α-helix forms within a continuous strech of the polypeptide chain N-term prototypical φ = -57 ° ψ = -47 ° 5.4 Å rise, 3.6 aa/turn ∴ 1.5 Å/aa C-term α-Helices have a dipole moment, due to unbonded and aligned N-H and C=O groups β-Sheets contain extended (β-strand) segments from separate regions of a protein prototypical φ = -139 °, ψ = +135 ° prototypical φ = -119 °, ψ = +113 ° (6.5Å repeat length in parallel sheet) Antiparallel β-sheets may be formed by closer regions of sequence than parallel Beta turn Figure 6-13 The stability of helices and sheets depends on their sequence of amino acids • Intrinsic propensity of an amino acid to adopt a helical or extended (strand) conformation The stability of helices and sheets depends on their sequence of amino acids • Intrinsic propensity of an amino acid to adopt a helical or extended (strand) conformation The stability of helices and sheets depends on their sequence of amino acids • Intrinsic propensity of an amino acid to adopt a helical or extended (strand) conformation • Interactions between adjacent R-groups – Ionic attraction or repulsion – Steric hindrance of adjacent bulky groups Helix wheel The stability of helices and sheets depends on their sequence of amino acids • Intrinsic propensity of an amino acid to adopt a helical or extended (strand) conformation • Interactions between adjacent R-groups – Ionic attraction or repulsion – Steric hindrance of adjacent bulky groups • Occurrence of proline and glycine • Interactions between ends of helix and aa R-groups His Glu N-term C-term
    [Show full text]
  • The Origin of the Eukaryotic Cell Based on Conservation of Existing
    The Origin of the Eukaryotic Albert D. G. de Roos The Beagle Armada Cell Based on Conservation Bioinformatics Division of Existing Interfaces Einsteinstraat 67 3316GG Dordrecht, The Netherlands [email protected] Abstract Current theories about the origin of the eukaryotic Keywords cell all assume that during evolution a prokaryotic cell acquired a Evolution, nucleus, eukaryotes, self-assembly, cellular membranes nucleus. Here, it is shown that a scenario in which the nucleus acquired a plasma membrane is inherently less complex because existing interfaces remain intact during evolution. Using this scenario, the evolution to the first eukaryotic cell can be modeled in three steps, based on the self-assembly of cellular membranes by lipid-protein interactions. First, the inclusion of chromosomes in a nuclear membrane is mediated by interactions between laminar proteins and lipid vesicles. Second, the formation of a primitive endoplasmic reticulum, or exomembrane, is induced by the expression of intrinsic membrane proteins. Third, a plasma membrane is formed by fusion of exomembrane vesicles on the cytoskeletal protein scaffold. All three self-assembly processes occur both in vivo and in vitro. This new model provides a gradual Darwinistic evolutionary model of the origins of the eukaryotic cell and suggests an inherent ability of an ancestral, primitive genome to induce its own inclusion in a membrane. 1 Introduction The origin of eukaryotes is one of the major challenges in evolutionary cell biology. No inter- mediates between prokaryotes and eukaryotes have been found, and the steps leading to eukaryotic endomembranes and endoskeleton are poorly understood. There are basically two competing classes of hypotheses: the endosymbiotic and the autogenic.
    [Show full text]
  • Modeling and Predicting Super-Secondary Structures of Transmembrane Beta-Barrel Proteins Thuong Van Du Tran
    Modeling and predicting super-secondary structures of transmembrane beta-barrel proteins Thuong van Du Tran To cite this version: Thuong van Du Tran. Modeling and predicting super-secondary structures of transmembrane beta-barrel proteins. Bioinformatics [q-bio.QM]. Ecole Polytechnique X, 2011. English. NNT : 2011EPXX0104. pastel-00711285 HAL Id: pastel-00711285 https://pastel.archives-ouvertes.fr/pastel-00711285 Submitted on 23 Jun 2012 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. THESE` pr´esent´ee pour obtenir le grade de DOCTEUR DE L’ECOLE´ POLYTECHNIQUE Sp´ecialit´e: INFORMATIQUE par Thuong Van Du TRAN Titre de la th`ese: Modeling and Predicting Super-secondary Structures of Transmembrane β-barrel Proteins Soutenue le 7 d´ecembre 2011 devant le jury compos´ede: MM. Laurent MOUCHARD Rapporteurs Mikhail A. ROYTBERG MM. Gregory KUCHEROV Examinateurs Mireille REGNIER M. Jean-Marc STEYAERT Directeur Laboratoire d’Informatique UMR X-CNRS 7161 Ecole´ Polytechnique, 91128 Plaiseau CEDEX, FRANCE Composed with LATEX !c Thuong Van Du Tran. All rights reserved. Contents Introduction 1 1Fundamentalreviewofproteins 5 1.1 Introduction................................... 5 1.2 Proteins..................................... 5 1.2.1 Aminoacids............................... 5 1.2.2 Properties of amino acids .
    [Show full text]
  • Development and Characterization of Novel Bioluminescent Reporters of Cellular Activity by Derrick C. Cumberbatch Dissertation
    Development and Characterization of Novel Bioluminescent Reporters of Cellular Activity By Derrick C. Cumberbatch Dissertation Submitted to the Faculty of the Graduate School of Vanderbilt University in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY in Biological Sciences May 10, 2019 Nashville, Tennessee Approved: C. David Weaver, Ph.D. Douglas McMahon, Ph.D. Qi Zhang, Ph.D. Carl Johnson, Ph.D. To my beloved and supportive wife Alicia, and to my parents Cameron and Marcia Cumberbatch. ii ACKNOWLEDGEMENTS This work was made possible by financial support from the NIMH grants MH107713 and MH116150 awarded to Carl Johnson, Ph.D. as well as funds provided by the Vanderbilt University Dissertation Enhancement Grant, graciously awarded to me by the Graduate School. I appreciate Dr. Carl Johnson for taking me into his lab and providing me with ample tools that aided in the successful completion of my Ph.D. I would like to express gratitude to my committee members Drs. David Weaver, Douglas McMahon, Qi Zhang, and the late Dr. Donna Webb for guiding me through the process of becoming a competent researcher. I would also like to make special mention of Jie Yang, Ph.D. whose persistent efforts and sage advice were an ever-present help during my graduate studies. His one-on-one training provided me with many skills that will serve me well as a molecular biologist. Meaningful contributions from the other current and past members of the Johnson lab group, Yao Xu, Ph.D., Tetsuya Mori, Ph.D., Shuqun Shi, Ph.D., Chi Zhao, Ph.D., Peijun Ma, Ph.D., He Huang, Ph.D., Kathryn Campbell, Briana Wyzinski, Kevin Kelly, Maria Luisa Jabbur, Carla O’Neale and Ian Dew deserve to be highlighted here as well.
    [Show full text]
  • An Unusual Hydrophobic Core Confers Extreme Flexibility to HEAT Repeat Proteins
    1596 Biophysical Journal Volume 99 September 2010 1596–1603 An Unusual Hydrophobic Core Confers Extreme Flexibility to HEAT Repeat Proteins Christian Kappel, Ulrich Zachariae, Nicole Do¨lker, and Helmut Grubmu¨ller* Department of Theoretical and Computational Biophysics, Max Planck Institute for Biophysical Chemistry, Go¨ttingen, Germany ABSTRACT Alpha-solenoid proteins are suggested to constitute highly flexible macromolecules, whose structural variability and large surface area is instrumental in many important protein-protein binding processes. By equilibrium and nonequilibrium molecular dynamics simulations, we show that importin-b, an archetypical a-solenoid, displays unprecedentedly large and fully reversible elasticity. Our stretching molecular dynamics simulations reveal full elasticity over up to twofold end-to-end extensions compared to its bound state. Despite the absence of any long-range intramolecular contacts, the protein can return to its equilibrium structure to within 3 A˚ backbone RMSD after the release of mechanical stress. We find that this extreme degree of flexibility is based on an unusually flexible hydrophobic core that differs substantially from that of structurally similar but more rigid globular proteins. In that respect, the core of importin-b resembles molten globules. The elastic behavior is dominated by nonpolar interactions between HEAT repeats, combined with conformational entropic effects. Our results suggest that a-sole- noid structures such as importin-b may bridge the molecular gap between completely structured and intrinsically disordered proteins. INTRODUCTION Solenoid proteins, consisting of repeating arrays of simple on repeat proteins focus on the folding and unfolding basic structural motifs, account for >5% of the genome of mechanism (14–16), an atomic force microscopy study on multicellular organisms (1).
    [Show full text]
  • Bioinformatics: a Practical Guide to the Analysis of Genes and Proteins, Second Edition Andreas D
    BIOINFORMATICS A Practical Guide to the Analysis of Genes and Proteins SECOND EDITION Andreas D. Baxevanis Genome Technology Branch National Human Genome Research Institute National Institutes of Health Bethesda, Maryland USA B. F. Francis Ouellette Centre for Molecular Medicine and Therapeutics Children’s and Women’s Health Centre of British Columbia University of British Columbia Vancouver, British Columbia Canada A JOHN WILEY & SONS, INC., PUBLICATION New York • Chichester • Weinheim • Brisbane • Singapore • Toronto BIOINFORMATICS SECOND EDITION METHODS OF BIOCHEMICAL ANALYSIS Volume 43 BIOINFORMATICS A Practical Guide to the Analysis of Genes and Proteins SECOND EDITION Andreas D. Baxevanis Genome Technology Branch National Human Genome Research Institute National Institutes of Health Bethesda, Maryland USA B. F. Francis Ouellette Centre for Molecular Medicine and Therapeutics Children’s and Women’s Health Centre of British Columbia University of British Columbia Vancouver, British Columbia Canada A JOHN WILEY & SONS, INC., PUBLICATION New York • Chichester • Weinheim • Brisbane • Singapore • Toronto Designations used by companies to distinguish their products are often claimed as trademarks. In all instances where John Wiley & Sons, Inc., is aware of a claim, the product names appear in initial capital or ALL CAPITAL LETTERS. Readers, however, should contact the appropriate companies for more complete information regarding trademarks and registration. Copyright ᭧ 2001 by John Wiley & Sons, Inc. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic or mechanical, including uploading, downloading, printing, decompiling, recording or otherwise, except as permitted under Sections 107 or 108 of the 1976 United States Copyright Act, without the prior written permission of the Publisher.
    [Show full text]
  • Synthesis and Nmr Studies of a Β-Turn Mimetic Molecular
    SYNTHESIS AND NMR STUDIES OF A β-TURN MIMETIC MOLECULAR TORSION BALANCE by Melissa Ann Liberatore B.S. Chemistry, Lehigh University, 2006 Submitted to the Graduate Faculty of the Kenneth P. Dietrich School of Arts and Sciences in partial fulfillment of the requirements for the degree of Doctor of Philosophy University of Pittsburgh 2012 UNIVERSITY OF PITTSBURGH DIETRICH SCHOOL OF ARTS AND SCIENCES This dissertation was presented by Melissa Ann Liberatore It was defended on July 23, 2012 and approved by Professor Dennis Curran, Department of Chemistry Professor Michael Trakselis, Department of Chemistry Professor Judith Klein-Seetharaman, Department of Structural Biology Dissertation Advisor: Professor Craig Wilcox, Department of Chemistry ii Copyright © by Melissa Ann Liberatore 2012 iii SYNTHESIS AND NMR STUDIES OF A β-TURN MIMETIC MOLECULAR TORSION BALANCE Melissa Ann Liberatore, PhD University of Pittsburgh, 2012 The attainment of precise measurements of the molecular forces that influence protein folding is important in order to further understand peptide dynamics and stability. A hybrid synthetic- natural peptide motif, combining an o,o,o’-trisubstituted biphenyl with an (ortho-tolyl)-amide, was synthesized in multiple formats and studied by NMR to probe the effects of amino acid substitutions on antiparallel beta-sheet configuration and stability. The potential of this “molecular torsion balance” as a beta-turn mimic was demonstrated by quantifying the rotational barriers about several axes. The free-energy rotational barrier of the aryl-aryl bond was found to be 35.7 kcal mol-1 at 418 K in hexanes. EXSY analysis was also used to measure barriers about -1 -1 the N-aryl (20.9 kcal mol at 343 K in toluene-d8) and N-CO bonds (17.2 kcal mol at 298 K in chloroform-d).
    [Show full text]
  • Proteome-Scale Prediction of Structure and Func- Tion
    Downloaded from genome.cshlp.org on October 5, 2021 - Published by Cold Spring Harbor Laboratory Press The proteome folding project: proteome-scale prediction of structure and func- tion Kevin Drew 1, Patrick Winters 1, Glenn L. Butterfoss 1, Viktors Berstis 2, Keith Uplinger 2, Jonathan Armstrong 2, Michael Riffle 3, Erik Schweighofer 4, Bill Bovermann 2, David R. Good- lett 5, Trisha N. Davis 3, Dennis Shasha 6, Lars Malmström 7, Richard Bonneau 1,4,6 * 1 Center for Genomics and Systems Biology, Department of Biology, New York University, New York, NY 10003, USA 2 IBM, Austin, TX, 78758, USA 3 Department of Biochemistry, Department of Genome Sciences, University of Washington, Seattle, WA 98195, USA 4 Institute for Systems Biology, Seattle, WA 98103, USA 5 Medicinal Chemistry Department, University of Washington, Seattle, WA 98195, USA 6 Department of Computer Science, Courant Institute of Mathematical Sciences, New York University, New York, New York, 10003, USA 7 Institute of Molecular Systems Biology, ETH Zurich, Zurich CH 8093, Switzerland * To whom correspondence should be addressed. Richard Bonneau, PhD. New York University Center for Genomics and Systems Biology 100 Washington Sq. E. 1009 Main Building New York, NY 10003 Voice: 646 460 3026 Email: [email protected] Running title: proteome folding Keywords: proteome, de novo folding, function prediction, Rosetta, grid computing 1 Downloaded from genome.cshlp.org on October 5, 2021 - Published by Cold Spring Harbor Laboratory Press 2 Downloaded from genome.cshlp.org on October 5, 2021 - Published by Cold Spring Harbor Laboratory Press Abstract: The incompleteness of proteome structure and function annotation is a critical problem for biol- ogists and, in particular, severely limits interpretation of high-throughput and next-generation experiments.
    [Show full text]
  • The Development of the Prediction of Protein Structure
    6 The Development of the Prediction of Protein Structure Gerald D. Fasman I. Introduction .................................................................... 194 II. Protein Topology. .. 196 III. Techniques of Protein Prediction ................................................... 198 A. Sequence Alignment .......................................................... 199 B. Hydrophobicity .............................................................. 200 C. Minimum Energy Calculations ................................................. 202 IV. Approaches to Protein Conformation ................................................ 203 A. Solvent Accessibility ......................................................... 203 B. Packing of Residues .......................................................... 204 C. Distance Geometry ........................................................... 205 D. Amino Acid Physicochemical Properties ......................................... 205 V. Prediction of the Secondary Structure of Proteins: a Helix, ~ Strands, and ~ Turn .......... 208 A. ~ Turns .................................................................... 209 B. Evaluation of Predictive Methodologies .......................................... 218 C. Other Predictive Algorithms ................................................... 222 D. Chou-Fasman Algorithm ...................................................... 224 E. Class Prediction ............................................................. 233 VI. Prediction of Tertiary Structure ...................................................
    [Show full text]