DOCSLIB.ORG

Active Noise Control Over Space: a Subspace Method for Performance Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Active Noise Control Over Space: a Subspace Method for Performance Analysis applied sciences Article Active Noise Control over Space: A Subspace Method for Performance Analysis Jihui Zhang 1,* , Thushara D. Abhayapala 1 , Wen Zhang 1,2 and Prasanga N. Samarasinghe 1 1 Audio & Acoustic Signal Processing Group, College of Engineering and Computer Science, Australian National University, Canberra 2601, Australia; [email protected] (T.D.A.); [email protected] (W.Z.); [email protected] (P.N.S.) 2 Center of Intelligent Acoustics and Immersive Communications, School of Marine Science and Technology, Northwestern Polytechnical University, Xi0an 710072, China * Correspondence: [email protected] Received: 28 February 2019; Accepted: 20 March 2019; Published: 25 March 2019 Abstract: In this paper, we investigate the maximum active noise control performance over a three-dimensional (3-D) spatial space, for a given set of secondary sources in a particular environment. We first formulate the spatial active noise control (ANC) problem in a 3-D room. Then we discuss a wave-domain least squares method by matching the secondary noise field to the primary noise field in the wave domain. Furthermore, we extract the subspace from wave-domain coefficients of the secondary paths and propose a subspace method by matching the secondary noise field to the projection of primary noise field in the subspace. Simulation results demonstrate the effectiveness of the proposed algorithms by comparison between the wave-domain least squares method and the subspace method, more specifically the energy of the loudspeaker driving signals, noise reduction inside the region, and residual noise field outside the region. We also investigate the ANC performance under different loudspeaker configurations and noise source positions. Keywords: active noise control (ANC); performance analysis; wave domain; spatial noise; reverberant room 1. Introduction Active noise control (ANC) over a spatially extended region, which is termed as ‘Spatial ANC’, is a challenging field of research as the aim is to create a large quiet zone for multiple listeners in three-dimensional (3-D) spaces. In spatial ANC applications, such as noise cancellation in aircraft [1] and automobiles [2–5], multichannel ANC systems equipped with multiple sensors and multiple secondary sources are adopted [6]. In literature, both time-domain [7,8] and frequency-domain [9,10] algorithms have been implemented in multichannel ANC systems, which can cancel the noise at error sensor positions and their close surroundings [10]. Recently, ANC over space has been approached via Wave field synthesis (WFS)-based wave-domain algorithms [11–13] and (cylindrical/spherical) harmonic-based wave-domain algorithms [14–19], with which the noise over entire region of interest can be cancelled directly. Here onwards, we use the terminology ‘wave-domain ANC’ to refer to harmonics-based wave-domain ANC. In wave-domain ANC, the number of secondary sources/loudspeakers is required to be no less than the number of modes in the spatial region, so that all the modes can be controlled. When the number of loudspeakers cannot control all the modes in the spatial region, using the wave-domain adaptive algorithms and conventional adaptive algorithms, the noise reduction performance in the steady state degrades significantly [16]. In practical applications, numbers and locations of the Appl. Sci. 2019, 9, 1250; doi:10.3390/app9061250 www.mdpi.com/journal/applsci Appl. Sci. 2019, 9, 1250 2 of 20 loudspeakers have more constraints compared to simulation setups in [16]. For instance, in a vehicle, the numbers and positions of the loudspeakers are highly constrained by the vehicle dimensions and passenger convenience. It is valuable for design engineers to estimate whether the available numbers and positions of the loudspeakers are sufficient to the noise reduction requirements, before they implement an ANC system in a real environment. Since the noise reduction performance varies with different ANC algorithms, it is important to investigate the maximum achievable performance for the given system, which is dependent on the coherence between the reference sensors and the error sensors [20], secondary source characteristics and locations, room environments, and the primary noise field characteristics. In the literature, Laugesen et al. provided the theoretical prediction for multichannel ANC in a small reverberant room based on the primary signal on the error sensors [21]. For spatial ANC performance estimation over an entire region, Chen et al. investigated ANC performance by noise pattern analysis of the primary noise field [22,23]. Buerger et al. investigated the coherence between two observation points in the noise field evoked by given continuous source distributions, which can be applied to predict the upper bound of ANC performance in the region of interest [24]. However, the capability of secondary sources, in particular room environments, has not yet been explored. In this paper, we investigate the maximum noise control performance over a spatial region by investigating capability of secondary sources, in particular room environments. We define the subspace spanned by the wave-domain secondary-path coefficients, and evaluate the ANC performance in the subspace. Using the proposed subspace method, the design engineers can predict the noise cancellation performance before an actual ANC system is implemented in a product. Simulations are conducted in a 3-D room environment under different noise source positions, when the loudspeakers have constraints on numbers and positions. The proposed subspace method is more feasible than the wave-domain least squares method. The rest of this paper is organized as follows. In Section2, we formulate the ANC problem in a 3-D room. We investigate the maximum ANC performance using the wave-domain least squares method in Section3, and investigate the maximum ANC performance using the subspace method in Section4. The simulation validation is demonstrated in Section5. We draw some conclusions in Section6. 2. Problem Formulation In this section, we formulate the ANC problem in the wave domain to cancel the noise over a 3-D spatial region inside rooms. As shown in Figure1, let the quiet zone of interest (blue area) be a spherical region (S) with a radius R1. Assume that the noise sources (black stars) and the secondary sources (black loudspeakers) are located outside the region of interest. In the ANC process, we measure the noise field by placing a spherical microphone array (dark blue stars) on the boundary of the control region (i.e., the desired quiet zone). Any arbitrary observation point within the control region is denoted as x ≡ fr, fx, yxg. Here, y and f are the elevation angle and the azimuthal angle, respectively. In the ANC system, the residual signal at this point e(x, k) is given by e(x, k) = n(x, k) + s(x, k), (1) where k = 2p f /c is the wave number, f is the frequency, and c is the speed of sound propagation. n(x, k) and s(x, k) denote the primary noise field and the secondary noise field observed at point x, respectively. Appl. Sci. 2019, 9, 1250 3 of 20 The secondary noise field generated by a discrete loudspeaker array with L loudspeakers (A simple model of the loudspeaker is applied here. More models characterizing the acoustic, mechanic and electric system of the loudspeakers are investigated in [25].) can be represented by L s(x, k) = ∑ dl(k)G(xjyl, k), (2) l=1 th th where dl(k) is the driving signal for the l loudspeaker, yl denotes the location of the l loudspeaker, th and G(xjyl, k) denotes the acoustic transfer function (ATF) between the l loudspeaker and the observation point x. Please note that in the reverberant environment, G(xjyl, k) includes the room reflections. Figure 1. ANC system in a 3-D room. Black stars represent primary sources, loudspeakers represent secondary sources, the blue sphere represents the control region, and dark blue stars represent error microphones over the control region. Instead of using measurements of the microphone signals directly, the wave-domain approach employs the wave equation solutions as basis functions to express any wave field over the spatial region, and designs the secondary noise field based on the wave-domain decomposition coefficients. We then represent the primary noise field and secondary noise field in the wave domain. The spherical harmonics-based wave equation solution decomposes any homogeneous incident wave field n(x, k) observed at x into ¥ u n(x, k) = ∑ ∑ bum(k)ju(kr)Yum(fx, yx), (3) u=0 m=−u where ju(·) is the spherical Bessel function of order u and Yum(·) denotes the spherical harmonics. Therefore, the decomposition coefficients bum(k) represent the primary noise field in the wave domain. Within the region of interest r ≤ R1, a finite number of modes can be used to approximate the noise field [26]. Thus, the primary noise field in (3) can be truncated by N u n(x, k) ≈ ∑ ∑ bum(k)ju(kr)Yum(fx, yx), (4) u=0 m=−u Appl. Sci. 2019, 9, 1250 4 of 20 where the truncation order of N = dekR1/2e [26–28]. In the vector version, b(k) = [b0,0(k), b1,−1(k), T ..., bN,N(k)] . Using the spherical harmonic expansion, the secondary noise field within the quiet zone can also be represented by ¥ u s(x, k) = ∑ ∑ gum(k)ju(kr)Yum(fx, yx), (5) u=0 m=−u where the coefficients gum(k) represent the secondary noise field in the wave domain. Similar to the primary noise field, inside the region of interest with the radius of R1, the secondary noise field can be truncated by N u s(x, k) ≈ ∑ ∑ gum(k)ju(kr)Yum(fx, yx). (6) u=0 m=−u The ATF in (2) can be parameterized in the wave domain [29] as N u (l) G(xjyl, k) ≈ ∑ ∑ hum(k)ju(kr)Yum(fx, yx), (7) u=0 m=−u (l) where hum(k) is the ATF in wave domain for each loudspeaker.
Load more

Recommended publications
  • AN279: Estimating Period Jitter from Phase Noise
    AN279 ESTIMATING PERIOD JITTER FROM PHASE NOISE 1. Introduction This application note reviews how RMS period jitter may be estimated from phase noise data. This approach is useful for estimating period jitter when sufficiently accurate time domain instruments, such as jitter measuring oscilloscopes or Time Interval Analyzers (TIAs), are unavailable. 2. Terminology In this application note, the following definitions apply: Cycle-to-cycle jitter—The short-term variation in clock period between adjacent clock cycles. This jitter measure, abbreviated here as JCC, may be specified as either an RMS or peak-to-peak quantity. Jitter—Short-term variations of the significant instants of a digital signal from their ideal positions in time (Ref: Telcordia GR-499-CORE). In this application note, the digital signal is a clock source or oscillator. Short- term here means phase noise contributions are restricted to frequencies greater than or equal to 10 Hz (Ref: Telcordia GR-1244-CORE). Period jitter—The short-term variation in clock period over all measured clock cycles, compared to the average clock period. This jitter measure, abbreviated here as JPER, may be specified as either an RMS or peak-to-peak quantity. This application note will concentrate on estimating the RMS value of this jitter parameter. The illustration in Figure 1 suggests how one might measure the RMS period jitter in the time domain. The first edge is the reference edge or trigger edge as if we were using an oscilloscope. Clock Period Distribution J PER(RMS) = T = 0 T = TPER Figure 1. RMS Period Jitter Example Phase jitter—The integrated jitter (area under the curve) of a phase noise plot over a particular jitter bandwidth.
    [Show full text]
  • A Deep Learning Approach to Active Noise Control
    A Deep Learning Approach to Active Noise Control Hao Zhang1, DeLiang Wang1;2 1Department of Computer Science and Engineering, The Ohio State University, USA 2Center for Cognitive and Brain Sciences, The Ohio State University, USA fzhang.6720, [email protected] Abstract Reference Error Microphone �(�) Microphone �(�) We formulate active noise control (ANC) as a supervised �(�) �(�) �(�) learning problem and propose a deep learning approach, called �(�) deep ANC, to address the nonlinear ANC problem. A convo- lutional recurrent network (CRN) is trained to estimate the real Cancelling Loudspeaker �(�) and imaginary spectrograms of the canceling signal from the reference signal so that the corresponding anti-noise can elimi- ANC nate or attenuate the primary noise in the ANC system. Large- scale multi-condition training is employed to achieve good gen- Figure 1: Diagram of a single-channel feedforward ANC sys- eralization and robustness against a variety of noises. The deep tem, where P (z) and S(z) denote the frequency responses of ANC method can be trained to achieve active noise cancella- primary path and secondary path, respectively. tion no matter whether the reference signal is noise or noisy speech. In addition, a delay-compensated strategy is intro- tional link artificial neural network to handle the nonlinear ef- duced to address the potential latency problem of ANC sys- fect in ANC. Other nonlinear adaptive models such as radial tems. Experimental results show that the proposed method is basis function networks [12], fuzzy neural networks [13], and effective for wide-band noise reduction and generalizes well to recurrent neural networks [14] have been developed to further untrained noises.
    [Show full text]
  • Active Noise Control in a Three-Dimensional Space Jihe Yang Iowa State University
    Iowa State University Capstones, Theses and Retrospective Theses and Dissertations Dissertations 1994 Active noise control in a three-dimensional space Jihe Yang Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/rtd Part of the Acoustics, Dynamics, and Controls Commons, and the Physics Commons Recommended Citation Yang, Jihe, "Active noise control in a three-dimensional space " (1994). Retrospective Theses and Dissertations. 10660. https://lib.dr.iastate.edu/rtd/10660 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Retrospective Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. U'M'I MICROFILMED 1994 INFORMATION TO USERS This manuscript has been reproduced from the microfilm master. UMI films the text directly from the original or copy submitted. Thus, some thesis and dissertation copies are in typewriter face, while others may be from any type of computer printer. The quality of this reproduction is dependent upon the quality of the copy submitted. Broken or indistinct print, colored or poor quality illustrations and photographs, print bleedthrough, substandard margins, and improper alignment can adversely affect reproduction. In the unlikely event that the author did not send UMI a complete manuscript and there are missing pages, these vrill be noted. Also, if unauthorized copyright material had to be removed, a note will indicate the deletion. Oversize materials (e.g., maps, drawings, charts) are reproduced by sectioning the original, beginning at the upper left-hand comer and continuing from left to right in equal sections with small overlaps.
    [Show full text]
  • Signal-To-Noise Ratio and Dynamic Range Definitions
    Signal-to-noise ratio and dynamic range definitions The Signal-to-Noise Ratio (SNR) and Dynamic Range (DR) are two common parameters used to specify the electrical performance of a spectrometer. This technical note will describe how they are defined and how to measure and calculate them. Figure 1: Definitions of SNR and SR. The signal out of the spectrometer is a digital signal between 0 and 2N-1, where N is the number of bits in the Analogue-to-Digital (A/D) converter on the electronics. Typical numbers for N range from 10 to 16 leading to maximum signal level between 1,023 and 65,535 counts. The Noise is the stochastic variation of the signal around a mean value. In Figure 1 we have shown a spectrum with a single peak in wavelength and time. As indicated on the figure the peak signal level will fluctuate a small amount around the mean value due to the noise of the electronics. Noise is measured by the Root-Mean-Squared (RMS) value of the fluctuations over time. The SNR is defined as the average over time of the peak signal divided by the RMS noise of the peak signal over the same time. In order to get an accurate result for the SNR it is generally required to measure over 25 -50 time samples of the spectrum. It is very important that your input to the spectrometer is constant during SNR measurements. Otherwise, you will be measuring other things like drift of you lamp power or time dependent signal levels from your sample.
    [Show full text]
  • Image Denoising by Autoencoder: Learning Core Representations
    Image Denoising by AutoEncoder: Learning Core Representations Zhenyu Zhao College of Engineering and Computer Science, The Australian National University, Australia, [email protected] Abstract. In this paper, we implement an image denoising method which can be generally used in all kinds of noisy images. We achieve denoising process by adding Gaussian noise to raw images and then feed them into AutoEncoder to learn its core representations(raw images itself or high-level representations).We use pre- trained classifier to test the quality of the representations with the classification accuracy. Our result shows that in task-specific classification neuron networks, the performance of the network with noisy input images is far below the preprocessing images that using denoising AutoEncoder. In the meanwhile, our experiments also show that the preprocessed images can achieve compatible result with the noiseless input images. Keywords: Image Denoising, Image Representations, Neuron Networks, Deep Learning, AutoEncoder. 1 Introduction 1.1 Image Denoising Image is the object that stores and reflects visual perception. Images are also important information carriers today. Acquisition channel and artificial editing are the two main ways that corrupt observed images. The goal of image restoration techniques [1] is to restore the original image from a noisy observation of it. Image denoising is common image restoration problems that are useful by to many industrial and scientific applications. Image denoising prob- lems arise when an image is corrupted by additive white Gaussian noise which is common result of many acquisition channels. The white Gaussian noise can be harmful to many image applications. Hence, it is of great importance to remove Gaussian noise from images.
    [Show full text]
  • Frequency Domain Active Noise Control with Ultrasonic Tracking Thomas Chapin Waite Iowa State University
    Iowa State University Capstones, Theses and Graduate Theses and Dissertations Dissertations 2010 Frequency Domain Active Noise Control with Ultrasonic Tracking Thomas Chapin Waite Iowa State University Follow this and additional works at: https://lib.dr.iastate.edu/etd Part of the Mechanical Engineering Commons Recommended Citation Waite, Thomas Chapin, "Frequency Domain Active Noise Control with Ultrasonic Tracking" (2010). Graduate Theses and Dissertations. 11782. https://lib.dr.iastate.edu/etd/11782 This Dissertation is brought to you for free and open access by the Iowa State University Capstones, Theses and Dissertations at Iowa State University Digital Repository. It has been accepted for inclusion in Graduate Theses and Dissertations by an authorized administrator of Iowa State University Digital Repository. For more information, please contact [email protected]. Frequency domain active noise control with ultrasonic tracking by Tom Waite A dissertation submitted to the graduate faculty in partial fulfillment of the requirements for the degree of DOCTOR OF PHILOSOPHY Major: Mechanical Engineering Program of Study Committee: Atul G. Kelkar, Major Professor Julie A. Dickerson J. Adin Mann III Jerald M. Vogel Qingze Zou Iowa State University Ames, Iowa 2010 Copyright c Tom Waite, 2010. All rights reserved. ii TABLE OF CONTENTS LIST OF FIGURES . v ACKNOWLEDGEMENTS . xi ABSTRACT . xii CHAPTER 1. INTRODUCTION . 1 1.1 Background . 1 1.1.1 Frequency Domain ANC . 5 1.1.2 Ultrasonic Tracking . 7 1.2 Outline . 8 CHAPTER 2. ULTRASONIC TRACKING . 11 2.1 Introduction . 11 2.2 Localization . 11 2.2.1 Bandwidth Considerations . 16 2.3 Error . 18 2.3.1 Sources of Incorrect Solutions .
    [Show full text]
  • Noise and Vibration Control in the Built Environment
    applied sciences Noise and Vibration Control in the Built Environment Edited by Jian Kang Printed Edition of the Special Issue Published in Applied Sciences www.mdpi.com/journal/applsci Noise and Vibration Control in the Built Environment Special Issue Editor Jian Kang Special Issue Editor Jian Kang University of Sheffield UK Editorial Office MDPI AG St. Alban-Anlage 66 Basel, Switzerland This edition is a reprint of the Special Issue published online in the open access journal Applied Sciences (ISSN 2076-3417) from 2016–2017 (available at: http://www.mdpi.com/journal/applsci/special_issues/vibration_control). For citation purposes, cite each article independently as indicated on the article page online and as indicated below: Author 1; Author 2; Author 3 etc. Article title. Journal Name. Year. Article number/page range. ISBN 978-3-03842-420-8 (Pbk) ISBN 978-3-03842-421-5 (PDF) Articles in this volume are Open Access and distributed under the Creative Commons Attribution license (CC BY), which allows users to download, copy and build upon published articles even for commercial purposes, as long as the author and publisher are properly credited, which ensures maximum dissemination and a wider impact of our publications. The book taken as a whole is © 2017 MDPI, Basel, Switzerland, distributed under the terms and conditions of the Creative Commons license CC BY-NC-ND (http://creativecommons.org/licenses/by-nc-nd/4.0/). Table of Contents About the Guest Editor .............................................................................................................................. v Preface to “Noise and Vibration Control in the Built Environment” ................................................... vii Chapter 1: Urban Sound Environment and Soundscape Francesco Aletta, Federica Lepore, Eirini Kostara-Konstantinou, Jian Kang and Arianna Astolfi An Experimental Study on the Influence of Soundscapes on People’s Behaviour in an Open Public Space Reprinted from: Appl.
    [Show full text]
  • Noise Reduction Through Active Noise Control Using Stereophonic Sound for Increasing Quite Zone
    Noise reduction through active noise control using stereophonic sound for increasing quite zone Dongki Min1; Junjong Kim2; Sangwon Nam3; Junhong Park4 1,2,3,4 Hanyang University, Korea ABSTRACT The low frequency impact noise generated during machine operation is difficult to control by conventional active noise control. The Active Noise Control (ANC) is a destructive interference technic of noise source and control sound by generating anti-phase control sound. Its efficiency is limited to small space near the error microphones. At different locations, the noise level may increase due to control sounds. In this study, the ANC method using stereophonic sound was investigated to reduce interior low frequency noise and increase the quite zone. The Distance Based Amplitude Panning (DBAP) algorithm based on the distance between the virtual sound source and the speaker was used to create a virtual sound source by adjusting the volume proportions of multi speakers respectively. The 3-Dimensional sound ANC system was able to change the position of virtual control source using DBAP algorithm. The quiet zone was formed using fixed multi speaker system for various locations of noise sources. Keywords: Active noise control, stereophonic sound I-INCE Classification of Subjects Number(s): 38.2 1. INTRODUCTION The noise reduction is a main issue according to improvement of living condition. There are passive and active control methods for noise reduction. The passive noise control uses sound absorption material which has efficiency about high frequency. The Active Noise Control (ANC) which is the method for generating anti phase control sound is able to reduce low frequency.
    [Show full text]
  • AN-839 RMS Phase Jitter
    RMS Phase Jitter AN-839 APPLICATION NOTE Introduction In order to discuss RMS Phase Jitter, some basics phase noise theory must be understood. Phase noise is often considered an important measurement of spectral purity which is the inherent stability of a timing signal. Phase noise is the frequency domain representation of random fluctuations in the phase of a waveform caused by time domain instabilities called jitter. An ideal sinusoidal oscillator, with perfect spectral purity, has a single line in the frequency spectrum. Such perfect spectral purity is not achievable in a practical oscillator where there are phase and frequency fluctuations. Phase noise is a way of describing the phase and frequency fluctuation or jitter of a timing signal in the frequency domain as compared to a perfect reference signal. Generating Phase Noise and Frequency Spectrum Plots Phase noise data is typically generated from a frequency spectrum plot which can represent a time domain signal in the frequency domain. A frequency spectrum plot is generated via a Fourier transform of the signal, and the resulting values are plotted with power versus frequency. This is normally done using a spectrum analyzer. A frequency spectrum plot is used to define the spectral purity of a signal. The noise power in a band at a specific offset (FO) from the carrier frequency (FC) compared to the power of the carrier frequency is called the dBc Phase Noise. Power Level of a 1Hz band at an offset (F ) dBc Phase Noise = O Power Level of the carrier Frequency (FC) A Phase Noise plot is generated using data from the frequency spectrum plot.
    [Show full text]
  • Multi-Channel Active Noise Control for All Uncertain Primary and Secondary Paths
    Multi-channel Active Noise Control for All Uncertain Primary and Secondary Paths Yuhsuke Ohta and Akira Sano Department of System Design Engineering, Keio University, 3-14-1 Hiyoshi, Kohoku-ku, Yokohama 223-8522, Japan Abstract filter matrices in an on-line manner, which enables the noise cancellation at the objective points. Unlike the pre- Fully adaptive feedforward control algorithm is proposed vious indirect approaches based on the explicit on-line for general multi-channel active noise control (ANC) identification, neither dither sounds nor the PE property when all the noise transmission channels are uncertain. of the source noises are required in the proposed scheme. To reduce the actual canceling error, two kinds of virtual errors are introduced and are forced into zero by adjusting 2. Feedforward Adaptive Active Noise Control three adaptive FIR filter matrices in an on-line manner, which can result in the canceling at the objective points. Primary Reference Secondary Error Noise Microphones Sources Microphones Unlike other conventional approaches, the proposed algo- Sources G (z) rithm does not need exact identification of the secondary 1 e1 (k) paths, and so requires neither any dither signals nor the v1(k) s1 (k) PE property of the source noises, which is a great advan- r1(k) G (z) tage of the proposed adaptive approach. 3 G2 (z) G4 (z) s(k) 1. Introduction vN (k) c e (k) Nc s (k) Ns r (k) Active noise control (ANC) is efficiently used to sup- Nr press unwanted low frequency noises generated from pri- mary sources by emitting artificial secondary sounds to u(k) r(k) Adaptice Active objective points [1][2].
    [Show full text]
  • Noise Element
    10 NOISE ELEMENT A. Introduction Noise is defined as a sound or series of sounds that are considered to be inva- sive, irritating, objectionable, and/or disruptive to the quality of daily life. Noise varies in range and volume and can originate from individual incidents such as construction equipment, sporadic disturbances, such as car horns or train whistles, or more constant irritants, such as traffic along major arterials. Section 65302(f) of the California Government Code requires that General Plans contain a Noise Element that can be used as a guide for establishing a pattern of land uses that minimizes the exposure of community residents to excessive noise. Local governments are required to analyze and quantify noise levels and the extent of noise exposure through field measurements or noise modeling, and implement measures and possible solutions to existing and foreseeable noise problems. This section describes the existing noise environment in Los Gatos and is di- vided into the following sections: ♦ Introduction: A description of the scope, requirements, and contents of the Noise Element. ♦ Noise Background and Terminology: A description of noise issues, stan- dards, and terminology used to describe noise. ♦ Noise Standards: A summary of outdoor noise limits established by Los Gatos. ♦ Sources of Existing Noise: A summary of the sources of noise, including stationary, non-stationary, and construction noise sources. ♦ Future Noise Contours: A description of projected noise conditions in Los Gatos at General Plan buildout. ♦ Goals, Policies, and Actions: A list of goal, policy, and action statements that are intended to mitigate and reduce noise impacts in Los Gatos.
    [Show full text]
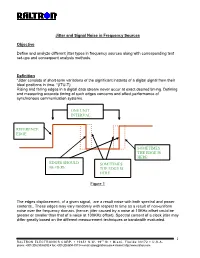
  • Jitter and Signal Noise in Frequency Sources
    Jitter and Signal Noise in Frequency Sources Objective Define and analyze different jitter types in frequency sources along with corresponding test set-ups and consequent analysis methods. Definition “Jitter consists of short-term variations of the significant instants of a digital signal from their ideal positions in time. “(ITU-T) Rising and falling edges in a digital data stream never occur at exact desired timing. Defining and measuring accurate timing of such edges concerns and affect performance of synchronous communication systems. ONE UNIT INTERVAL REFERENCE EDGE SOMETIMES THE EDGE IS HERE EDGES SHOULD SOMETIMES BE HERE THE EDGE IS HERE Figure 1 The edges displacement, of a given signal, are a result noise with both spectral and power contents.. These edges may vary randomly with respect to time as a result of non-uniform noise over the frequency domain. (hence; jitter caused by a noise at 10KHz offset could be greater or smaller than that of a noise at 100KHz offset). Spectral content of a clock jitter may differ greatly based on the different measurement techniques or bandwidth evaluated. 1 RALTRON ELECTRONICS CORP. ! 10651 N.W. 19th St ! Miami, Florida 33172 ! U.S.A. phone: +001(305) 593-6033 ! fax: +001(305)594-3973 ! e-mail: [email protected] ! internet: http://www.raltron.com System Disruptions caused by Jitter Clock recovery mechanisms, in network elements, are used to sample the digital signal using the recovered bit clock. If the digital signal and the clock have identical jitter, the constant jitter error will not affect the sampling instant and therefore no bit errors will arise.
    [Show full text]