Measurement Uncertainty and Significant Figures There Is No Such
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Check Points for Measuring Instruments
Catalog No. E12024 Check Points for Measuring Instruments Introduction Measurement… the word can mean many things. In the case of length measurement there are many kinds of measuring instrument and corresponding measuring methods. For efficient and accurate measurement, the proper usage of measuring tools and instruments is vital. Additionally, to ensure the long working life of those instruments, care in use and regular maintenance is important. We have put together this booklet to help anyone get the best use from a Mitutoyo measuring instrument for many years, and sincerely hope it will help you. CONVENTIONS USED IN THIS BOOKLET The following symbols are used in this booklet to help the user obtain reliable measurement data through correct instrument operation. correct incorrect CONTENTS Products Used for Maintenance of Measuring Instruments 1 Micrometers Digimatic Outside Micrometers (Coolant Proof Micrometers) 2 Outside Micrometers 3 Holtest Digimatic Holtest (Three-point Bore Micrometers) 4 Holtest (Two-point/Three-point Bore Micrometers) 5 Bore Gages Bore Gages 6 Bore Gages (Small Holes) 7 Calipers ABSOLUTE Coolant Proof Calipers 8 ABSOLUTE Digimatic Calipers 9 Dial Calipers 10 Vernier Calipers 11 ABSOLUTE Inside Calipers 12 Offset Centerline Calipers 13 Height Gages Digimatic Height Gages 14 ABSOLUTE Digimatic Height Gages 15 Vernier Height Gages 16 Dial Height Gages 17 Indicators Digimatic Indicators 18 Dial Indicators 19 Dial Test Indicators (Lever-operated Dial Indicators) 20 Thickness Gages 21 Gauge Blocks Rectangular Gauge Blocks 22 Products Used for Maintenance of Measuring Instruments Mitutoyo products Micrometer oil Maintenance kit for gauge blocks Lubrication and rust-prevention oil Maintenance kit for gauge Order No.207000 blocks includes all the necessary maintenance tools for removing burrs and contamination, and for applying anti-corrosion treatment after use, etc. -
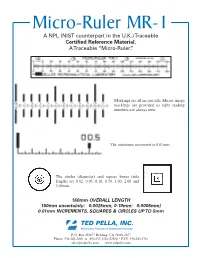
Micro-Ruler MR-1 a NPL (NIST Counterpart in the U.K.)Traceable Certified Reference Material
Micro-Ruler MR-1 A NPL (NIST counterpart in the U.K.)Traceable Certified Reference Material . ATraceable “Micro-Ruler”. Markings are all on one side. Mirror image markings are provided so right reading numbers are always seen. The minimum increment is 0.01mm. The circles (diameter) and square boxes (side length) are 0.02, 0.05, 0.10, 0.50, 1.00, 2.00 and 5.00mm. 150mm OVERALL LENGTH 150mm uncertainty: ±0.0025mm, 0-10mm: ±0.0005mm) 0.01mm INCREMENTS, SQUARES & CIRCLES UP TO 5mm TED PELLA, INC. Microscopy Products for Science and Industry P. O. Box 492477 Redding, CA 96049-2477 Phone: 530-243-2200 or 800-237-3526 (USA) • FAX: 530-243-3761 [email protected] www.tedpella.com DOES THE WORLD NEED A TRACEABLE RULER? The MR-1 is labeled in mm. Its overall scale extends According to ISO, traceable measurements shall be over 150mm with 0.01mm increments. The ruler is designed to be viewed from either side as the markings made when products require the dimensions to be are both right reading and mirror images. This allows known to a specified uncertainty. These measurements the ruler marking to be placed in direct contact with the shall be made with a traceable ruler or micrometer. For sample, avoiding parallax errors. Independent of the magnification to be traceable the image and object size ruler orientation, the scale can be read correctly. There is must be measured with calibration standards that have a common scale with the finest (0.01mm) markings to traceable dimensions. read. We measure and certify pitch (the distance between repeating parallel lines using center-to-center or edge-to- edge spacing. -

Verification Regulation of Steel Ruler
ITTC – Recommended 7.6-02-04 Procedures and guidelines Page 1 of 15 Effective Date Revision Calibration of Micrometers 2002 00 ITTC Quality System Manual Sample Work Instructions Work Instructions Calibration of Micrometers 7.6 Control of Inspection, Measuring and Test Equipment 7.6-02 Sample Work Instructions 7.6-02-04 Calibration of Micrometers Updated / Edited by Approved Quality Systems Group of the 28th ITTC 23rd ITTC 2002 Date: 07/2017 Date: 09/2002 ITTC – Recommended 7.6-02-04 Procedures and guidelines Page 2 of 15 Effective Date Revision Calibration of Micrometers 2002 00 Table of Contents 1. PURPOSE .............................................. 4 4.6 MEASURING FORCE ......................... 9 4.6.1 Requirements: ............................... 9 2. INTRODUCTION ................................. 4 4.6.2 Calibration Method: ..................... 9 3. SUBJECT AND CONDITION OF 4.7 WIDTH AND WIDTH DIFFERENCE CALIBRATION .................................... 4 OF LINES .............................................. 9 3.1 SUBJECT AND MAIN TOOLS OF 4.7.1 Requirements ................................ 9 CALIBRATION .................................... 4 4.7.2 Calibration Method ...................... 9 3.2 CALIBRATION CONDITIONS .......... 5 4.8 RELATIVE POSITION OF INDICATOR NEEDLE AND DIAL.. 10 4. TECHNICAL REQUIREMENTS AND CALIBRATION METHOD ................. 7 4.8.1 Requirements .............................. 10 4.8.2 Calibration Method: ................... 10 4.1 EXTERIOR ............................................ 7 4.9 DISTANCE -

Vernier Caliper and Micrometer Computer Models Using Easy Java Simulation and Its Pedagogical Design Features—Ideas for Augmenting Learning with Real Instruments
Wee, Loo Kang, & Ning, Hwee Tiang. (2014). Vernier caliper and micrometer computer models using Easy Java Simulation and its pedagogical design features—ideas for augmenting learning with real instruments. Physics Education, 49(5), 493. Vernier caliper and micrometer computer models using Easy Java Simulation and its pedagogical design feature-ideas to augment learning with real instruments Loo Kang WEE1, Hwee Tiang NING2 1Ministry of Education, Educational Technology Division, Singapore 2 Ministry of Education, National Junior College, Singapore [email protected], [email protected] Abstract: This article presents the customization of EJS models, used together with actual laboratory instruments, to create an active experiential learning of measurements. The laboratory instruments are the vernier caliper and the micrometer. Three computer model design ideas that complement real equipment are discussed in this article. They are 1) the simple view and associated learning to pen and paper question and the real world, 2) hints, answers, different options of scales and inclusion of zero error and 3) assessment for learning feedback. The initial positive feedback from Singaporean students and educators points to the possibility of these tools being successfully shared and implemented in learning communities, and validated. Educators are encouraged to change the source codes of these computer models to suit their own purposes, licensed creative commons attribution for the benefit of all humankind. Video abstract: http://youtu.be/jHoA5M-_1R4 2015 Resources: http://iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/5-vernier-caliper http://iwant2study.org/ospsg/index.php/interactive-resources/physics/01-measurements/6-micrometer Keyword: easy java simulation, active learning, education, teacher professional development, e–learning, applet, design, open source physics PACS: 06.30.Gv 06.30.Bp 1.50.H- 01.50.Lc 07.05.Tp I. -

Intro to Measurement Uncertainty 2011
Measurement Uncertainty and Significant Figures There is no such thing as a perfect measurement. Even doing something as simple as measuring the length of a pencil with a ruler is subject to limitations that can affect how close your measurement is to its true value. For example, you need to consider the clarity and accuracy of the scale on the ruler. What is the smallest subdivision of the ruler scale? How thick are the black lines that indicate centimeters and millimeters? Such ideas are important in understanding the limitations of use of a ruler, just as with any measuring device. The degree to which a measured quantity compares to the true value of the measurement describes the accuracy of the measurement. Most measuring instruments you will use in physics lab are quite accurate when used properly. However, even when an instrument is used properly, it is quite normal for different people to get slightly different values when measuring the same quantity. When using a ruler, perception of when an object is best lined up against the ruler scale may vary from person to person. Sometimes a measurement must be taken under less than ideal conditions, such as at an awkward angle or against a rough surface. As a result, if the measurement is repeated by different people (or even by the same person) the measured value can vary slightly. The degree to which repeated measurements of the same quantity differ describes the precision of the measurement. Because of limitations both in the accuracy and precision of measurements, you can never expect to be able to make an exact measurement. -

The Gage Block Handbook
AlllQM bSflim PUBUCATIONS NIST Monograph 180 The Gage Block Handbook Ted Doiron and John S. Beers United States Department of Commerce Technology Administration NET National Institute of Standards and Technology The National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303. Major technical operating units and their principal -

1201 Lab Manual Table of Contents
1201 LAB MANUAL TABLE OF CONTENTS WARNING: The Pasco carts & track components have strong magnets inside of them. Strong magnetic fields can affect pacemakers, ICDs and other implanted medical devices. Many of these devices are made with a feature that deactivates it with a magnetic field. Therefore, care must be taken to keep medical devices minimally 1’ away from any strong magnetic field. Introduction 3 Laboratory Skills Laboratory I: Physics Laboratory Skills 7 Problem #1: Constant Velocity Motion 1 9 Problem #2: Constant Velocity Motion 2 15 Problem #3: Measurement and Uncertainty 21 Laboratory I Cover Sheet 31 General Laws of Motion Laboratory II: Motion and Force 33 Problem #1: Falling 35 Problem #2: Motion Down an Incline 39 Problem #3: Motion Up and Down an Incline 43 Problem #4: Normal Force and Frictional Force 47 Problem #5: Velocity and Force 51 Problem #6: Two-Dimensional Motion 55 Table of Coefficients of Friction 59 Check Your Understanding 61 Laboratory II Cover Sheet 63 Laboratory III: Statics 65 Problem #1: Springs and Equilibrium I 67 Problem #2: Springs and Equilibrium II 71 Problem #3: Leg Elevator 75 Problem #4: Equilibrium of a Walkway 79 Problem #5: Designing a Mobile 83 Problem #6: Mechanical Arm 87 Check Your Understanding 91 Laboratory III Cover Sheet 93 Laboratory IV: Circular Motion and Rotation 95 Problem #1: Circular Motion 97 Problem #2: Rotation and Linear Motion at Constant Speed 101 Problem #3: Angular and Linear Acceleration 105 Problem #4: Moment of Inertia of a Complex System 109 Problem #5: Moments -

Surftest SJ-400
Form Measurement Surftest SJ-400 Bulletin No. 2013 Aurora, Illinois (Corporate Headquarters) (630) 978-5385 Westford, Massachusetts (978) 692-8765 Portable Surface Roughness Tester Huntersville, North Carolina (704) 875-8332 Mason, Ohio (513) 754-0709 Plymouth, Michigan (734) 459-2810 City of Industry, California (626) 961-9661 Kirkland, Washington (408) 396-4428 Surftest SJ-400 Series Revolutionary New Portable Surface Roughness Testers Make Their Debut Long-awaited performance and functionality are here: compact design, skidless and high-accuracy roughness measurements, multi-functionality and ease of operation. Requirement Requirement High-accuracy1 measurements with 3 Cylinder surface roughness measurements with a hand-held tester a hand-held tester A wide range, high-resolution detector and an ultra-straight drive The skidless measurement and R-surface compensation functions unit provide class-leading accuracy. make it possible to evaluate cylinder surface roughness. Detector Measuring range: 800µm Resolution: 0.000125µm (on 8µm range) Drive unit Straightness/traverse length SJ-401: 0.3µm/.98"(25mm) SJ-402: 0.5µm/1.96"(50mm) SJ-401 SJ-402 SJ-401 Requirement Requirement Roughness parameters2 that conform to international standards The SJ-400 Series can evaluate 36 kinds of roughness parameters conforming to the latest ISO, DIN, and ANSI standards, as well as to JIS standards (1994/1982). 4 Measurement/evaluation of stepped features and straightness Ultra-fine steps, straightness and waviness are easily measured by switching to skidless measurement mode. The ruler function enables simpler surface feature evaluation on the LCD monitor. 2 3 Requirement Measurement Applications R-surface 5 measurement Advanced data processing with extended analysis The SJ-400 Series allows data processing identical to that in the high-end class. -

Length Scale Measurement Procedures at the National Bureau of 1 Standards
NEW NIST PUBLICATION June 12, 1989 NBSIR 87-3625 Length Scale Measurement Procedures at the National Bureau of 1 Standards John S. Beers, Guest Worker U.S. DEPARTMENT OF COMMERCE National Bureau of Standards National Engineering Laboratory Precision Engineering Division Gaithersburg, MD 20899 September 1987 U.S. DEPARTMENT OF COMMERCE NBSIR 87-3625 LENGTH SCALE MEASUREMENT PROCEDURES AT THE NATIONAL BUREAU OF STANDARDS John S. Beers, Guest Worker U.S. DEPARTMENT OF COMMERCE National Bureau of Standards National Engineering Laboratory Precision Engineering Division Gaithersburg, MD 20899 September 1987 U.S. DEPARTMENT OF COMMERCE, Clarence J. Brown, Acting Secretary NATIONAL BUREAU OF STANDARDS, Ernest Ambler, Director LENGTH SCALE MEASUREMENT PROCEDURES AT NBS CONTENTS Page No Introduction 1 1.1 Purpose 1 1.2 Line scales of length 1 1.3 Line scale calibration and measurement assurance at NBS 2 The NBS Line Scale Interferometer 2 2.1 Evolution of the instrument 2 2.2 Original design and operation 3 2.3 Present form and operation 8 2.3.1 Microscope system electronics 8 2.3.2 Interferometer 9 2.3.3 Computer control and automation 11 2.4 Environmental measurements 11 2.4.1 Temperature measurement and control 13 2.4.2 Atmospheric pressure measurement 15 2.4.3 Water vapor measurement and control 15 2.5 Length computations 15 2.5.1 Fringe multiplier 16 2.5.2 Analysis of redundant measurements 17 3. Measurement procedure 18 Planning and preparation 18 Evaluation of the scale 18 Calibration plan 19 Comparator preparation 20 Scale preparation, -

Stride Ruler Use Your Own Two Feet to Estimate Distances
www.exploratorium.edu/geometryplayground/activities Stride Ruler Use your own two feet to estimate distances. Materials Background • playground or other paved You don’t always need a precise answer. A well-informed guess—an estimate—is surface often good enough. For example, you can estimate the time it will take you to walk • 4 metersticks to a neighborhood store and back. Your estimate may differ from the actual time by • masking tape a few minutes, but it will tell you if you have time go to the store and be back by • pencil dinnertime. Estimating distances is often useful, too, and that’s what you’ll find out • clipboard or book to create a how to do in this activity. sturdy writing surface Try This Group Size 1. Two volunteers should lay the metersticks end to end in a straight line on the whole group pavement, placing the 1-cm end of a meterstick against the 100-cm end of the previous one. Tape the metersticks securely to the pavement. Then tape a “start Related Activity line” perpendicular to the beginning of the first meter stick. Everyone should • Measuring and Mapping the take a turn doing the rest of the steps. Playground Did You Know? No measurement is exact. In a 4. sense, every measurement you 3. make is an estimate, no matter 2. how carefully you measure. (It’s been said, in fact, that while 1. counting is difficult, measuring is impossible!) St art Line 2. Put your toes just behind the “start line.” Take 10 “baby steps” forward, walking right next to the line of metersticks. -

MICHIGAN STATE COLLEGE Paul W
A STUDY OF RECENT DEVELOPMENTS AND INVENTIONS IN ENGINEERING INSTRUMENTS Thai: for III. Dean. of I. S. MICHIGAN STATE COLLEGE Paul W. Hoynigor I948 This]: _ C./ SUPP! '3' Nagy NIH: LJWIHL WA KOF BOOK A STUDY OF RECENT DEVELOPMENTS AND INVENTIONS IN ENGINEERING’INSIRUMENTS A Thesis Submitted to The Faculty of MICHIGAN‘STATE COLLEGE OF AGRICULTURE AND.APPLIED SCIENCE by Paul W. Heyniger Candidate for the Degree of Batchelor of Science June 1948 \. HE-UI: PREFACE This Thesis is submitted to the faculty of Michigan State College as one of the requirements for a B. S. De- gree in Civil Engineering.' At this time,I Iish to express my appreciation to c. M. Cade, Professor of Civil Engineering at Michigan State Collegeafor his assistance throughout the course and to the manufacturers,vhose products are represented, for their help by freely giving of the data used in this paper. In preparing the laterial used in this thesis, it was the authors at: to point out new develop-ants on existing instruments and recent inventions or engineer- ing equipment used principally by the Civil Engineer. 20 6052 TAEEE OF CONTENTS Chapter One Page Introduction B. Drafting Equipment ----------------------- 13 Chapter Two Telescopic Inprovenents A. Glass Reticles .......................... -32 B. Coated Lenses .......................... --J.B Chapter three The Tilting Level- ............................ -33 Chapter rear The First One-Second.Anerican Optical 28 “00d011 ‘6- -------------------------- e- --------- Chapter rive Chapter Six The Latest Type Altineter ----- - ................ 5.5 TABLE OF CONTENTS , Chapter Seven Page The Most Recent Drafting Machine ........... -39.--- Chapter Eight Chapter Nine SmOnnB By Radar ....... - ------------------ In”.-- Chapter Ten Conclusion ------------ - ----- -. -

MODULE 5 – Measuring Tools
INTRODUCTION TO MACHINING 2. MEASURING TOOLS AND PROCESSES: In this chapter we will only look at those instruments which would typically be used during and at the end of a fabrication process. Such instruments would be capable of measuring up to 4 decimal places in the inch system and up to 3 decimal places in the metric system. Higher precision is normally not required in shop settings. The discrimination of a measuring instrument is the number of “segments” to which it divides the basic unit of length it is using for measurement. As a rule of thumb: the discrimination of the instrument should be ~10 times finer than the dimension specified. For example if a dimension of 25.5 [mm] is specified, an instrument that is capable of measuring to 0.01 or 0.02 [mm] should be used; if the specified dimension is 25.50 [mm], then the instrument’s discrimination should be 0.001 or 0.002 [mm]. The tools discussed here can be divided into 2 categories: direct measuring tools and indirect measuring or comparator tools. 50 INTRODUCTION TO MACHINING 2.1 Terminology: Accuracy: can have two meanings: it may describe the conformance of a specific dimension with the intended value (e.g.: an end-mill has a specific diameter stamped on its shank; if that value is confirmed by using the appropriate measuring device, then the end-mill diameter is said to be accurate). Accuracy may also refer to the act of measuring: if the machinist uses a steel rule to verify the diameter of the end-mill, then the act of measuring is not accurate.