Transmuted Probability Distributions: a Review
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Miguel De Carvalho
School of Mathematics Miguel de Carvalho Contact M. de Carvalho T: +44 (0) 0131 650 5054 Information The University of Edinburgh B: [email protected] School of Mathematics : mb.carvalho Edinburgh EH9 3FD, UK +: www.maths.ed.ac.uk/ mdecarv Personal Born September 20, 1980 in Montijo, Lisbon. Details Portuguese and EU citizenship. Interests Applied Statistics, Biostatistics, Econometrics, Risk Analysis, Statistics of Extremes. Education Universidade de Lisboa, Portugal Habilitation in Probability and Statistics, 2019 Thesis: Statistical Modeling of Extremes Universidade Nova de Lisboa, Portugal PhD in Mathematics with emphasis on Statistics, 2009 Thesis: Extremum Estimators and Stochastic Optimization Advisors: Manuel Esqu´ıvel and Tiago Mexia Advisors of Advisors: Jean-Pierre Kahane and Tiago de Oliveira. Nova School of Business and Economics (Triple Accreditation), Portugal MSc in Economics, 2009 Thesis: Mean Regression for Censored Length-Biased Data Advisors: Jos´eA. F. Machado and Pedro Portugal Advisors of Advisors: Roger Koenker and John Addison. Universidade Nova de Lisboa, Portugal `Licenciatura'y in Mathematics, 2004 Professional Probation Period: Statistics Portugal (Instituto Nacional de Estat´ıstica). Awards & ISBA (International Society for Bayesian Analysis) Honours Lindley Award, 2019. TWAS (Academy of Sciences for the Developing World) Young Scientist Prize, 2015. International Statistical Institute Elected Member, 2014. American Statistical Association Young Researcher Award, Section on Risk Analysis, 2011. National Institute of Statistical Sciences j American Statistical Association Honorary Mention as a Finalist NISS/ASA Best y-BIS Paper Award, 2010. Portuguese Statistical Society (Sociedade Portuguesa de Estat´ıstica) Young Researcher Award, 2009. International Association for Statistical Computing ERS IASC Young Researcher Award, 2008. 1 of 13 p l e t t si a o e igulctoson Applied Statistical ModelingPublications 1. -

Abbreviations of Names of Serials
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). ∗ not previously listed E available electronically The abbreviation is followed by the complete title, the place of publication § journal reviewed cover-to-cover V videocassette series and other pertinent information. † monographic series ¶ bibliographic journal E 4OR 4OR. Quarterly Journal of the Belgian, French and Italian Operations Research ISSN 1211-4774. Societies. Springer, Berlin. ISSN 1619-4500. §Acta Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue Wuli † 19o Col´oq. Bras. Mat. 19o Col´oquio Brasileiro de Matem´atica. [19th Brazilian Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. (See also Acta Mathematics Colloquium] Inst. Mat. Pura Apl. (IMPA), Rio de Janeiro. Math.Sci.Ser.BEngl.Ed.) ISSN 1003-3998. † 24o Col´oq. Bras. Mat. 24o Col´oquio Brasileiro de Matem´atica. [24th Brazilian §ActaMath.Sci.Ser.BEngl.Ed. Acta Mathematica Scientia. Series B. English Edition. Mathematics Colloquium] Inst. Mat. Pura Apl. (IMPA), Rio de Janeiro. Science Press, Beijing. (See also Acta Math. Sci. Ser. A Chin. Ed.) ISSN 0252- † 25o Col´oq. Bras. Mat. 25o Col´oquio Brasileiro de Matem´atica. [25th Brazilian 9602. Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. § E Acta Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). Springer, † Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. Estonian Heidelberg. ISSN 1439-8516. Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. § E Acta Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. Chinese Series. Chinese Math. Abh. Braunschw. Wiss. Ges. Abhandlungen der Braunschweigischen Wissenschaftlichen Soc., Acta Math. -

Rank Full Journal Title Journal Impact Factor 1 Journal of Statistical
Journal Data Filtered By: Selected JCR Year: 2019 Selected Editions: SCIE Selected Categories: 'STATISTICS & PROBABILITY' Selected Category Scheme: WoS Rank Full Journal Title Journal Impact Eigenfactor Total Cites Factor Score Journal of Statistical Software 1 25,372 13.642 0.053040 Annual Review of Statistics and Its Application 2 515 5.095 0.004250 ECONOMETRICA 3 35,846 3.992 0.040750 JOURNAL OF THE AMERICAN STATISTICAL ASSOCIATION 4 36,843 3.989 0.032370 JOURNAL OF THE ROYAL STATISTICAL SOCIETY SERIES B-STATISTICAL METHODOLOGY 5 25,492 3.965 0.018040 STATISTICAL SCIENCE 6 6,545 3.583 0.007500 R Journal 7 1,811 3.312 0.007320 FUZZY SETS AND SYSTEMS 8 17,605 3.305 0.008740 BIOSTATISTICS 9 4,048 3.098 0.006780 STATISTICS AND COMPUTING 10 4,519 3.035 0.011050 IEEE-ACM Transactions on Computational Biology and Bioinformatics 11 3,542 3.015 0.006930 JOURNAL OF BUSINESS & ECONOMIC STATISTICS 12 5,921 2.935 0.008680 CHEMOMETRICS AND INTELLIGENT LABORATORY SYSTEMS 13 9,421 2.895 0.007790 MULTIVARIATE BEHAVIORAL RESEARCH 14 7,112 2.750 0.007880 INTERNATIONAL STATISTICAL REVIEW 15 1,807 2.740 0.002560 Bayesian Analysis 16 2,000 2.696 0.006600 ANNALS OF STATISTICS 17 21,466 2.650 0.027080 PROBABILISTIC ENGINEERING MECHANICS 18 2,689 2.411 0.002430 BRITISH JOURNAL OF MATHEMATICAL & STATISTICAL PSYCHOLOGY 19 1,965 2.388 0.003480 ANNALS OF PROBABILITY 20 5,892 2.377 0.017230 STOCHASTIC ENVIRONMENTAL RESEARCH AND RISK ASSESSMENT 21 4,272 2.351 0.006810 JOURNAL OF COMPUTATIONAL AND GRAPHICAL STATISTICS 22 4,369 2.319 0.008900 STATISTICAL METHODS IN -

Abbreviations of Names of Serials
Abbreviations of Names of Serials This list gives the form of references used in Mathematical Reviews (MR). ∗ not previously listed The abbreviation is followed by the complete title, the place of publication x journal indexed cover-to-cover and other pertinent information. y monographic series Update date: January 30, 2018 4OR 4OR. A Quarterly Journal of Operations Research. Springer, Berlin. ISSN xActa Math. Appl. Sin. Engl. Ser. Acta Mathematicae Applicatae Sinica. English 1619-4500. Series. Springer, Heidelberg. ISSN 0168-9673. y 30o Col´oq.Bras. Mat. 30o Col´oquioBrasileiro de Matem´atica. [30th Brazilian xActa Math. Hungar. Acta Mathematica Hungarica. Akad. Kiad´o,Budapest. Mathematics Colloquium] Inst. Nac. Mat. Pura Apl. (IMPA), Rio de Janeiro. ISSN 0236-5294. y Aastaraam. Eesti Mat. Selts Aastaraamat. Eesti Matemaatika Selts. [Annual. xActa Math. Sci. Ser. A Chin. Ed. Acta Mathematica Scientia. Series A. Shuxue Estonian Mathematical Society] Eesti Mat. Selts, Tartu. ISSN 1406-4316. Wuli Xuebao. Chinese Edition. Kexue Chubanshe (Science Press), Beijing. ISSN y Abel Symp. Abel Symposia. Springer, Heidelberg. ISSN 2193-2808. 1003-3998. y Abh. Akad. Wiss. G¨ottingenNeue Folge Abhandlungen der Akademie der xActa Math. Sci. Ser. B Engl. Ed. Acta Mathematica Scientia. Series B. English Wissenschaften zu G¨ottingen.Neue Folge. [Papers of the Academy of Sciences Edition. Sci. Press Beijing, Beijing. ISSN 0252-9602. in G¨ottingen.New Series] De Gruyter/Akademie Forschung, Berlin. ISSN 0930- xActa Math. Sin. (Engl. Ser.) Acta Mathematica Sinica (English Series). 4304. Springer, Berlin. ISSN 1439-8516. y Abh. Akad. Wiss. Hamburg Abhandlungen der Akademie der Wissenschaften xActa Math. Sinica (Chin. Ser.) Acta Mathematica Sinica. -

CURRICULUM VITAE YAAKOV MALINOVSKY May 3, 2020
CURRICULUM VITAE YAAKOV MALINOVSKY May 3, 2020 University of Maryland, Baltimore County Email: [email protected] Department of Mathematics and Statistics Homepage: http://www.math.umbc.edu/ yaakovm 1000 Hilltop Circle Cell. No.: 240-535-1622 Baltimore, MD 21250 Education: Ph.D. 2009 The Hebrew University of Jerusalem, Israel Statistics M.A. 2002 The Hebrew University of Jerusalem, Israel Statistics with Operation Research B.A. 1999 The Hebrew University of Jerusalem, Israel Statistics (Summa Cum Laude) Experience in Higher Education: From July 1, 2017 , University of Maryland, Baltimore County, Associate Professor, Mathematics and Statistics. Fall 2011 { 2017, University of Maryland, Baltimore County, Assistant Professor, Mathematics and Statistics. September 2009 { August 2011, NICHD, Visiting Fellow. Spring 2003 { Spring 2007, The Hebrew University in Jerusalem, Instructor, Statistics. 2000{2004, The Open University, Israel, Instructor, Mathematics and Computer Science. Scholarships & Awards: 2014 IMS Meeting of New Researchers Travel award 2010 IMS Meeting of New Researchers Travel award 2003 Hebrew University Yochi Wax prize for PhD student 2001 Hebrew University Rector fellowship 1996 Hebrew University Dean's award 1995 Hebrew University Dean's list Academic visiting: Biostatistics Research Branch NIAID (June-August 2015), La Sapienza Rome Department of Mathematics (January 2018), Alfr´edR´enyi Institute of Mathematics Budapest (June 2018), Biostatistics Branch NCI (August 2017, August 2018, August 2019), Haifa University Department -

Distributions You Can Count on . . . but What's the Point? †
econometrics Article Distributions You Can Count On . But What’s the Point? † Brendan P. M. McCabe 1 and Christopher L. Skeels 2,* 1 School of Management, University of Liverpoo, Liverpool L69 7ZH, UK; [email protected] 2 Department of Economics, The University of Melbourne, Carlton VIC 3053, Australia * Correspondence: [email protected] † An early version of this paper was originally prepared for the Fest in Celebration of the 65th Birthday of Professor Maxwell King, hosted by Monash University. It was started while Skeels was visiting the Department of Economics at the University of Bristol. He would like to thank them for their hospitality and, in particular, Ken Binmore for a very helpful discussion. We would also like to thank David Dickson and David Harris for useful comments along the way. Received: 2 September 2019; Accepted: 25 February 2020; Published: 4 March 2020 Abstract: The Poisson regression model remains an important tool in the econometric analysis of count data. In a pioneering contribution to the econometric analysis of such models, Lung-Fei Lee presented a specification test for a Poisson model against a broad class of discrete distributions sometimes called the Katz family. Two members of this alternative class are the binomial and negative binomial distributions, which are commonly used with count data to allow for under- and over-dispersion, respectively. In this paper we explore the structure of other distributions within the class and their suitability as alternatives to the Poisson model. Potential difficulties with the Katz likelihood leads us to investigate a class of point optimal tests of the Poisson assumption against the alternative of over-dispersion in both the regression and intercept only cases. -

Daniel S. Cooley Education Academic and Professional Experience
Daniel S. Cooley Professor and Graduate Director Department of Statistics, Colorado State University, Fort Collins, CO 80523-1877 [email protected] www.stat.colostate.edu/∼cooleyd August 4, 2020 Education Ph.D. Applied Mathematics, University of Colorado at Boulder, 2005 M.S. Applied Mathematics, University of Colorado at Boulder, 2002 B.A. Mathematics, University of Colorado at Boulder, 1994 Academic and Professional Experience 2020-Present: Graduate Director; Department of Statistics, Colorado State University. 2018-Present: Professor; Department of Statistics, Colorado State University. 2017-2020: Associate Chair; Department of Statistics, Colorado State University. 2015-Present: Faculty Member; School of Environmental Sustainability, Colorado State University. 2012-2018: Associate Professor; Department of Statistics, Colorado State University. 2007-2012: Assistant Professor; Department of Statistics, Colorado State University. 2005-2007: Postdoctoral Researcher; Department of Statistics, Colorado State University (joint ap- pointment). 2005-2007: Postdoctoral Researcher; Geophysical Statistics Project, National Center for Atmo- spheric Research, (joint appointment). Visiting Appointments Fall 2014: Visiting Scholar; Department of Statistics, University of Washington, Seattle WA. Fall 2011: Research Fellow, Program on Uncertainty Quantification; SAMSI, Research Triangle Park, NC. June 2008: Invited Visitor; Institut de Recherche Math´ematiqueAvanc´ee,Universit´eLouis Pasteur Strasbourg, France. Research Interests Extreme value theory, modeling multivariate extremes, heavy tailed phenomena, spatial statistics, applications in atmospheric science and environmental science. Honors/Awards College of Natural Sciences, Professor Laureate, 2017-2019. ASA Section on Statistics and the Environment Young Researcher Award, 2012. ASA Section on Statistics and the Environment (ENVR) JSM Presentation Award for the paper \Spatial Prediction of Extreme Value Return Levels", August 2005. 1 Publications Research Articles, Refereed 1. -

Dissecting the Multivariate Extremal Index and Tail Dependence
REVSTAT – Statistical Journal Volume 18, Number 4, October 2020, 501–520 DISSECTING THE MULTIVARIATE EXTREMAL INDEX AND TAIL DEPENDENCE Authors: Helena Ferreira – Centro de Matem´atica e Aplica¸c˜oes(CMA-UBI), Universidade da Beira Interior, Avenida Marquˆesd’Avila e Bolama, 6200-001 Covilh˜a, Portugal [email protected] Marta Ferreira – Center of Mathematics of Minho University, Center for Computational and Stochastic Mathematics of University of Lisbon, Center of Statistics and Applications of University of Lisbon, Portugal [email protected] Received: April 2017 Revised: February 2018 Accepted: June 2018 Abstract: • A central issue in the theory of extreme values focuses on suitable conditions such that the well- known results for the limiting distributions of the maximum of i.i.d. sequences can be applied to stationary ones. In this context, the extremal index appears as a key parameter to capture the effect of temporal dependence on the limiting distribution of the maxima. The multivariate extremal index corresponds to a generalization of this concept to a multivariate context and affects the tail dependence structure within the marginal sequences and between them. As it is a function, the inference becomes more difficult, and it is therefore important to obtain characterizations, namely bounds based on the marginal dependence that are easier to estimate. In this work we present two decompositions that emphasize different types of information contained in the multivariate extremal index, an upper limit better than those found in the literature and we analyse its role in dependence on the limiting model of the componentwise maxima of a stationary sequence. We will illustrate the results with examples of recognized interest in applications. -

Spatio-Temporal Analysis of Regional Unemployment Rates: a Comparison of Model Based Approaches
REVSTAT – Statistical Journal Volume 16, Number 4, October 2018, 515–536 SPATIO-TEMPORAL ANALYSIS OF REGIONAL UNEMPLOYMENT RATES: A COMPARISON OF MODEL BASED APPROACHES Authors: Soraia Pereira – Faculdade de Ciˆencias, Universidade de Lisboa, Lisboa, Portugal [email protected] Feridun Turkman – Faculdade de Ciˆencias, Universidade de Lisboa, Lisboa, Portugal [email protected] Lu´ıs Correia – Instituto Nacional de Estat´ıstica, Lisboa, Portugal [email protected] Received: April 2016 Revised: November 2016 Accepted: November 2016 Abstract: • This study aims to analyze the methodologies that can be used to estimate the total number of unemployed, as well as the unemployment rates for 28 regions of Portugal, designated as NUTS III regions, using model based approaches as compared to the direct estimation methods currently employed by INE (National Statistical Institute of Portugal). Model based methods, often known as small area estimation methods (Rao, 2003), “borrow strength” from neighbouring regions and in doing so, aim to compensate for the small sample sizes often observed in these areas. Consequently, it is generally accepted that model based methods tend to produce estimates which have lesser variation. Other benefit in employing model based methods is the possibility of including auxiliary information in the form of variables of interest and latent random structures. This study focuses on the application of Bayesian hierarchical models to the Portuguese Labor Force Survey data from the 1st quarter of 2011 to the 4th quar- ter of 2013. Three different data modeling strategies are considered and compared: Modeling of the total unemployed through Poisson, Binomial and Negative Binomial models; modeling of rates using a Beta model; and modeling of the three states of the labor market (employed, unemployed and inactive) by a Multinomial model. -
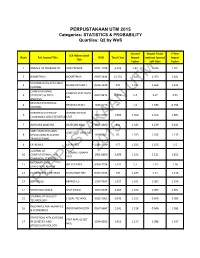
PERPUSTAKAAN UTM 2015 Categories: STATISTICS & PROBABILITY Quartiles: Q2 by Wos
PERPUSTAKAAN UTM 2015 Categories: STATISTICS & PROBABILITY Quartiles: Q2 by WoS Journal Impact Factor 5-Year JCR Abbreviated Rank Full Journal Title ISSN Total Cites Impact without Journal Impact Title Factor Self Cites Factor 1 ANNALS OF PROBABILITY ANN PROBAB 0091-1798 4,226 1.42 1.326 1.701 2 BIOMETRIKA BIOMETRIKA 0006-3444 15,774 1.418 1.359 2.281 SCANDINAVIAN ACTUARIAL 3 SCAND ACTUAR J 0346-1238 370 1.412 1.265 1.212 JOURNAL COMPUTATIONAL COMPUT STAT DATA UTM 4 STATISTICS & DATA 0167-9473 6,012 1.4 1.07 1.51 AN ANALYSIS REVSTAT-STATISTICAL 4 REVSTAT-STAT J 1645-6726 92 1.4 1.333 0.794 JOURNAL OXFORD BULLETIN OF OXFORD B ECON 6 0305-9049 1,986 1.368 1.356 1.885 ECONOMICS AND STATISTICS STAT 7 BAYESIAN ANALYSIS BAYESIAN ANAL 1931-6690 841 1.343 1.239 2.443 SORT-STATISTICS AND SORT-STAT OPER RES 8 OPERATIONS RESEARCH 1696-2281 85 1.333 1.292 1.133 T TRANSACTIONS 8 EXTREMES EXTREMES 1386-1999 457 1.333 1.156 1.5 JOURNAL OF J COMPUT GRAPH 2015 10 COMPUTATIONAL AND 1061-8600 2,699 1.222 1.121 1.812 STAT GRAPHICAL STATISTICS INTERNATIONAL 11 INT STAT REV 0306-7734 1,131 1.2 1.15 1.28 STATISTICAL REVIEW 12 ECONOMETRIC REVIEWS ECONOMET REV 0747-4938 730 1.189 1.17 1.116 13 BERNOULLIPERPUSTAKAANBERNOULLI 1350-7265 1,327 1.161 1.083 1.296 14 STATISTICA SINICA STAT SINICA 1017-0405 2,269 1.158 1.099 1.591 JOURNAL OF QUALITY 15 J QUAL TECHNOL 0022-4065 2,046 1.152 0.848 2.096 TECHNOLOGY INSURANCE MATHEMATICS 16 INSUR MATH ECON 0167-6687 2,141 1.128 0.646 1.582 & ECONOMICS STATISTICAL APPLICATIONS STAT APPL GENET 17 IN GENETICS AND 2194-6302 1,415 -

REVSTAT No 3
ISSN 1645-6726 Instituto Nacional de Estatística Statistics Portugal REVSTAT Statistical Journal Special issue on “Collection of Surveys on Tail Event Modeling" Guest Editors: Miguel de Carvalho Anthony C. Davison Jan Beirlant Volume 10, No.1 March 2012 REVSTAT STATISTICAL JOURNAL Catalogação Recomendada REVSTAT. Lisboa, 2003- Revstat : statistical journal / ed. Instituto Nacional de Estatística. - Vol. 1, 2003- . - Lisboa I.N.E., 2003- . - 30 cm Semestral. - Continuação de : Revista de Estatística = ISSN 0873-4275. - edição exclusivamente em inglês ISSN 1645-6726 CREDITS - EDITOR-IN-CHIEF - PUBLISHER - M. Ivette Gomes - Instituto Nacional de Estatística, I.P. (INE, I.P.) Av. António José de Almeida, 2 - CO-EDITOR 1000-043 LISBOA - M. Antónia Amaral Turkman PORTUGAL - ASSOCIATE EDITORS Tel.: + 351 218 426 100 - Barry Arnold Fax: + 351 218 426 364 - Helena Bacelar- Nicolau Web site: http://www.ine.pt - Susie Bayarri Customer Support Service - João Branco (National network): 808 201 808 - M. Lucília Carvalho (Other networks): + 351 226 050 748 - David Cox - COVER DESIGN - Edwin Diday - Mário Bouçadas, designed on the stain glass - Dani Gamerman window at INE, I.P., by the painter Abel Manta - Marie Husková - Isaac Meilijson - LAYOUT AND GRAPHIC DESIGN - M. Nazaré Mendes-Lopes - Carlos Perpétuo - Stephan Morgenthaler - PRINTING - António Pacheco - Instituto Nacional de Estatística, I.P. - Dinis Pestana - Ludger Rüschendorf - EDITION - Gilbert Saporta - 300 copies - Jef Teugels - LEGAL DEPOSIT REGISTRATION - EXECUTIVE EDITOR - N.º 191915/03 - Maria José Carrilho - SECRETARY - Liliana Martins PRICE [VAT included] - Single issue ……………………………………………………….. € 11 - Annual subscription (No. 1 Special Issue, No. 2 and No.3)………. € 26 - Annual subscription (No. 2, No. 3) ……………………………….. € 18 © INE, I.P., Lisbon. -
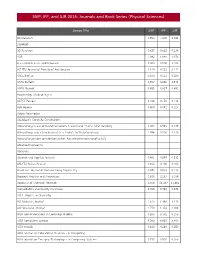
SNIP, IPP, and SJR 2015: Journals and Book Series (Physical Sciences)
SNIP, IPP, and SJR 2015: Journals and Book Series (Physical Sciences) Source Title SNIP IPP SJR 2D Materials 0.925 5.200 4.344 3 Biotech 3D Research 0.627 0.632 0.214 4OR 1.092 1.094 1.073 A + U-Architecture and Urbanism 0.000 0.000 0.100 A|Z ITU Journal of Faculty of Architecture 0.124 0.053 0.112 AACL Bioflux 0.474 0.351 0.200 AAPG Bulletin 1.907 3.330 1.978 AAPG Memoir 0.452 0.627 0.691 Aardkundige Mededelingen AATCC Review 0.266 0.250 0.134 ABB Review 0.404 0.091 0.127 Abbey Newsletter Aberdeen's Concrete Construction Abhandlungen aus dem Mathematischen Seminar der Universitat Hamburg 1.054 0.541 0.447 Abhandlungen der Senckenberg Gesellschaft fur Naturforschung 1.996 5.000 1.430 Abhandlungen der Senckenbergischen Naturforschenden Gesellschaft Abrasive Engineering Abrasives Abstract and Applied Analysis 0.441 0.579 0.512 ABU Technical Review 0.102 0.100 0.103 Academic Journal of Manufacturing Engineering 0.072 0.033 0.113 Accident Analysis and Prevention 1.628 2.213 1.109 Accounts of Chemical Research 4.506 21.467 11.465 Accreditation and Quality Assurance 0.965 0.740 0.378 ACH - Models in Chemistry ACI Materials Journal 1.620 1.446 1.430 ACI Structural Journal 1.750 1.354 2.088 ACM Communications in Computer Algebra 0.263 0.172 0.153 ACM Computing Surveys 8.265 6.633 3.405 ACM Inroads 0.630 0.248 0.250 ACM Journal on Educational Resources in Computing ACM Journal on Emerging Technologies in Computing Systems 0.735 0.932 0.366 Source Title SNIP IPP SJR ACM SIGPLAN Notices 0.803 0.571 0.490 ACM Transactions on Accessible Computing