Teaching System Identification Through Interactivity
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Exploring Collaborative Learning Methods in Leadership Development Programs Mary F
Walden University ScholarWorks Walden Dissertations and Doctoral Studies Walden Dissertations and Doctoral Studies Collection 2018 Exploring Collaborative Learning Methods in Leadership Development Programs Mary F. Woods Walden University Follow this and additional works at: https://scholarworks.waldenu.edu/dissertations Part of the Business Administration, Management, and Operations Commons, Management Sciences and Quantitative Methods Commons, and the Organizational Behavior and Theory Commons This Dissertation is brought to you for free and open access by the Walden Dissertations and Doctoral Studies Collection at ScholarWorks. It has been accepted for inclusion in Walden Dissertations and Doctoral Studies by an authorized administrator of ScholarWorks. For more information, please contact [email protected]. Walden University College of Management and Technology This is to certify that the doctoral dissertation by Mary F. Woods has been found to be complete and satisfactory in all respects, and that any and all revisions required by the review committee have been made. Review Committee Dr. Richard Schuttler, Committee Chairperson, Management Faculty Dr. Keri Heitner, Committee Member, Management Faculty Dr. Patricia Fusch, University Reviewer, Management Faculty Chief Academic Officer Eric Riedel, Ph.D. Walden University 2018 Abstract Exploring Collaborative Learning Methods in Leadership Development Programs by Mary F. Woods MA, Oakland City University, 2006 BS, Oakland City University, 2004 Dissertation Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy Management Walden University May 2018 Abstract Collaborative learning as it pertained to leadership development was an obscured method of learning. There was little research addressing the attributes contributing to collaborative learning for leadership development in leadership development programs. -
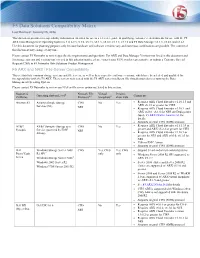
F5 Data Solutions Compatibility Matrix
F5 Data Solutions Compatibility Matrix Last Revised: January 25, 2016 This document provides interoperability information intended for use as a reference guide in qualifying customer’s environments for use with the F5 ARX Data Management Operating System 6.4.0, 6.x.x, 5.3.x, v5.2.x, v5.1.x, v5.0.x, v4.1.x, v3.2.x and F5 Data Manager v3.1.x, v3.0.x and v2.6.1. Use this document for planning purposes only because hardware and software versions vary and numerous combinations are possible. The content of this document may change at any time. Please contact F5 Networks to review specific site requirements and questions. For ARX and Data Manager Versions not listed in this document and for storage systems and versions not covered in this solution matrix, please contact your F5 Networks representative or submit a Customer Special Request (CSR) to F5 Networks Data Solutions Product Management. F5 ARX and NAS / File-Server Compatibility This section lists common storage systems and file servers, as well as their respective software versions, which have been tested and qualified for interoperability with the F5 ARX. These servers were tested with the F5 ARX series intelligent file virtualization devices running the Data Management Operating System. Please contact F5 Networks to review any NAS or file server option not listed in this section. Supported Network File Virtual Present- Operating System Level6 Comments Platforms Protocols1,2 Snapshots5 ation Vols. Amazon S3 Amazon Simple Storage CIFS No Yes Requires ARX Cloud Extender v1.10.1.3 and ARX v5.1.9 or greater for CIFS Services (S3) NFS Requires ARX Cloud Extender v1.10.1 and ARX v6.0.0, v6.1.0 for NFS see Deployment Guide F5 ARX DG for Amazon S3 for details. -

Bricscad® for Autocad® Users
BRICSCAD® FOR AUTOCAD® USERS Comparing User Interfaces Compatibility of Drawing Elements Customizing and Programming BricsCAD Operating Dual-CAD Design Offices Working in 3D BIM, Sheet Metal, & Communicator Updated for V18 Payment Information This book is covered by copyright. As the owner of the copyright, upFront.eZine Publishing, Ltd. gives you permission to make one print copy. You may not make any electronic copies, and you may not claim authorship or ownership of the text or figures herein. Suggested Price US$34.80 By Email Acrobat PDF format: Allow for a 15MB download. PayPal Check or Money Order To pay by PayPal, send payment to the account We can accept checks in the following of [email protected] at https://www.paypal.com/. currencies: • US funds drawn on a bank with address in the USA. Use this easy link to pay: • Canadian funds drawn on a bank with a Canadian https://www.paypal.me/upfrontezine/34.80 address (includes GST). PayPal accepts funds in US, Euro, Yen, Make cheque payable to ‘upFront.eZine Publishing’. Canadian, and 100+ other currencies. Please mail your payment to: “BricsCAD for AutoCAD Users” upFront.eZine Publishing, Ltd. 34486 Donlyn Avenue Abbotsford BC V2S 4W7 Canada Visit the BricsCAD for AutoCAD Users Web site at http://www.worldcadaccess.com/ebooksonline/. At this Web page, edi- tions of this book are available for BricsCAD V8 through V18. Purchasing an ebook published by upFront.eZine Publishing, Ltd. entitles you to receive the upFront.eZine newsletter weekly. To subscribe to this “The Business of CAD” newsletter separately, send an email to [email protected]. -

The Music of Ellen Taaffe Zwilich Performed by Faculty Members from Elizabethtown College
Society for American Music Fortieth Annual Conference Hosted by Elizabethtown College Lancaster Marriott at Penn Square 5–9 March 2014 Lancaster, Pennsylvania Mission of the Society for American Music he mission of the Society for American Music Tis to stimulate the appreciation, performance, creation, and study of American musics of all eras and in all their diversity, including the full range of activities and institutions associated with these musics throughout the world. ounded and first named in honor of Oscar Sonneck (1873–1928), the early Chief of the Library of Congress Music Division and the F pioneer scholar of American music, the Society for American Music is a constituent member of the American Council of Learned Societies. It is designated as a tax-exempt organization, 501(c)(3), by the Internal Revenue Service. Conferences held each year in the early spring give members the opportunity to share information and ideas, to hear performances, and to enjoy the company of others with similar interests. The Society publishes three periodicals. The Journal of the Society for American Music, a quarterly journal, is published for the Society by Cambridge University Press. Contents are chosen through review by a distinguished editorial advisory board representing the many subjects and professions within the field of American music.The Society for American Music Bulletin is published three times yearly and provides a timely and informal means by which members communicate with each other. The annual Directory provides a list of members, their postal and email addresses, and telephone and fax numbers. Each member lists current topics or projects that are then indexed, providing a useful means of contact for those with shared interests. -

F5 ARX Series F5 ARX Series
Datasheet F5 ARX Series F5 ARX Series ARX Series Intelligent File Virtualization Devices The industry’s most scalable, reliable platform for simplifying fi le storage Today’s fi le storage environments comprise a complex collection of storage platforms, fi le systems and operating systems that result in isolated islands of storage. Frequent outages occur when data is moved or new storage is provisioned due to the dependencies between clients and storage resources. Low aggregate utilization rates are common. Burgeoning capacity demands increase the operational overhead associated with fi le storage management. F5® ARX® devices allow you to break free from these constraints by introducing intelligent fi le virtualization into the fi le storage infrastructure — eliminating the disruption associated with storage administration and automating many storage management tasks. The result is a dramatic improvement in cost, agility and business effi ciency. Key Benefi ts Simplify File Storage with the F5 Acopia ARX Series • Multiple services in a single platform F5 Acopia ARX devices are high performance, highly available, intelligent fi le virtualization including Global Namespace, migration, systems that dramatically simplify fi le storage management. tiering, replication and load balancing True Heterogeneity • Industry-leading performance and scale ARX systems use industry standard fi le access protocols to communicate with clients and servers — CIFS for Windows® devices and NFS for Unix® or Linux devices. The ARX does • Uncompromising availability not introduce a new fi le system, but acts as a proxy to the fi le systems that are already • Real-time policy enforcement there. With the ARX, enterprises are not required to forklift upgrade hardware, or replace existing fi le systems, or install software agents across the enterprise, in order to • Enterprise-class manageability and gain the benefi ts of virtualization. -
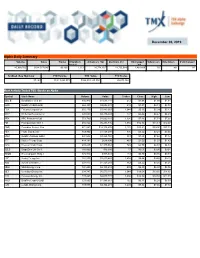
December 06, 2019 Alpha Daily Summary
December 06, 2019 Alpha Daily Summary Volume Value Trades # Symbols Advancers Vol Decliners Vol Unchanged # Advancers # Decliners # Unchanged traded Vol 40,990,706 $624,517,649 96,896 1,323 26,774,262 11,735,014 2,481,430 735 461 127 52-Week New High/Low YTD Volume YTD Value YTD Trades 87 / 43 10,813,298,973 $164,903,143,502 26,673,364 Most Actively Traded TSX Stocks on Alpha Symbol Stock Name Volume Value Trades Close High Low BBD.B Bombardier Cl B SV 816,940 $1,611,144 512 $1.98 $1.99 $1.94 HOD BetaPro CrdOil-2x Br 668,323 $2,652,531 210 $3.97 $4.11 $3.88 ECA EnCana Corporation 655,170 $3,483,663 1,044 $5.35 $5.39 $5.13 WCP Whitecap Resources J 620,609 $2,736,549 777 $4.44 $4.47 $4.29 ARX ARC Resources Ltd. 553,790 $4,060,801 1,304 $7.48 $7.53 $7.00 FM First Quantum Mnrl J 486,824 $6,293,736 1,954 $12.96 $13.13 $12.47 CNQ Canadian Natural Res 471,563 $18,116,876 2,122 $38.91 $39.00 $37.18 PEY Peyto Expl & Dev 459,900 $1,458,594 876 $3.22 $3.24 $3.05 HNU BetaPro NatGas 2xBul 441,542 $3,228,768 383 $7.23 $7.64 $7.12 BTE Baytex Energy Corp. 414,192 $618,890 467 $1.50 $1.52 $1.43 CPG Crescent Point Corp. 405,435 $1,935,563 745 $4.79 $4.83 $4.59 SZLS StageZero Life Sci J 380,000 $16,680 17 $0.05 $0.05 $0.04 TGOD Green Organic Hldg J 374,910 $305,041 133 $0.80 $0.85 $0.79 HSE Husky Energy Inc. -

Parallel Implementations of ARX-Based Block Ciphers on Graphic Processing Units
mathematics Article Parallel Implementations of ARX-Based Block Ciphers on Graphic Processing Units SangWoo An 1, YoungBeom Kim 2 , Hyeokdong Kwon 3, Hwajeong Seo 3 and Seog Chung Seo 2,* 1 Department of Financial Information Security, Kookmin University, Seoul 02707, Korea; [email protected] 2 Department of Information Security, Cryptology, and Mathematics, Kookmin University, Seoul 02707, Korea; [email protected] 3 Division of IT Convergence Engineering, Hansung University, Seoul 02876, Korea; [email protected] (H.K.); [email protected] (H.S.) * Correspondence: [email protected]; Tel.: +82-02-910-4742 Received: 23 August 2020; Accepted: 13 October 2020; Published: 31 October 2020 Abstract: With the development of information and communication technology, various types of Internet of Things (IoT) devices have widely been used for convenient services. Many users with their IoT devices request various services to servers. Thus, the amount of users’ personal information that servers need to protect has dramatically increased. To quickly and safely protect users’ personal information, it is necessary to optimize the speed of the encryption process. Since it is difficult to provide the basic services of the server while encrypting a large amount of data in the existing CPU, several parallel optimization methods using Graphics Processing Units (GPUs) have been considered. In this paper, we propose several optimization techniques using GPU for efficient implementation of lightweight block cipher algorithms on the server-side. As the target algorithm, we select high security and light weight (HIGHT), Lightweight Encryption Algorithm (LEA), and revised CHAM, which are Add-Rotate-Xor (ARX)-based block ciphers, because they are used widely on IoT devices. -

In Focus: Computing
CERNCOURIER IN FOCUS COMPUTING A retrospective of 60 years’ coverage of computing technology cerncourier.com 2019 COMPUTERS, WHY? 1972: CERN’s Lew Kowarski on how computers worked and why they were needed COMPUTING IN HIGH ENERGY PHYSICS 1989: CHEP conference considered the data challenges of the LEP era WEAVING A BETTER TOMORROW 1999: a snapshot of the web as it was beginning to take off THE CERN OPENLAB 2003: Grid computing was at the heart of CERN’s new industry partnership CCSupp_4_Computing_Cover_v3.indd 1 20/11/2019 13:54 CERNCOURIER WWW. I N F OCUS C OMPUT I N G CERNCOURIER.COM IN THIS ISSUE CERN COURIER IN FOCUS COMPUTING Best Cyclotron Systems provides 15/20/25/30/35/70 MeV Proton Cyclotrons as well as 35 & 70 MeV Multi-Particle (Alpha, Deuteron & Proton) Cyclotrons Motorola CERN Currents from 100uA to 1000uA (or higher) depending on the FROM THE EDITOR particle beam are available on all BCS cyclotrons Welcome to this retrospective Best 20u to 25 and 30u to 35 are fully upgradeable on site supplement devoted to Cyclotron Energy (MeV) Isotopes Produced computing – the fourth in 18F, 99mTc, 11C, 13N, 15O, a series celebrating CERN Best 15 15 64Cu, 67Ga, 124I, 103Pd Courier’s 60th anniversary. Big impact An early Data shift CERN’s Computer Centre in 1998, with banks of Best 15 + 123I, The Courier grew up during the microprocessor chip. 19 computing arrays for the major experiments. 25 Best 20u/25 20, 25–15 111 68 68 In, Ge/ Ga computing revolution. CERN’s first Best 30u Best 15 + 123I, SPECIAL FOREWORD 5 30 computer, the Ferranti Mercury, which (Upgradeable) 111In, 68Ge/68Ga CERN computing guru Graeme Stewart describes the immense task of had less computational ability than an taming future data volumes in high-energy physics. -
Corelcad 2019 Reviewer's Guide
Contents 1 | Introducing CorelCAD 2019 ...........................................................2 2 | Customer profiles ..........................................................................4 3 | Key features ...................................................................................7 4 | Integrating CorelCAD 2019 into other graphics workflows.................18 5 | Comparing CorelCAD 2019 to Light CAD applications....................20 [ 1 ] Reviewer’s Guide Introducing CorelCAD™ 2019 CorelCAD™ 2019 delivers superior 2D drafting supports opening and saving to AutoCAD 2018 and 3D design tools that let graphics .DWG, offering robust handling of file professionals enhance their visual communi- attributes of non-supported AutoCAD features cation with precision. It’s the smart, affordable and preserving functionality in .DWG files, solution for drawing the detailed elements eliminating conversion and sharing issues. required for technical design. CorelCAD For those who’ve worked with other popular provides an enhanced UI for workflow CAD tools, making the transition to CorelCAD efficiency and native .DWG file support for 2019 is straightforward. CorelCAD incorporates compatibility with all major CAD programs. a range of intuitive tools, commands, and With optimization for Windows and macOS, familiar UI elements found in other CAD you can enjoy improved speed and impressive software so any CAD designer can quickly get performance on the platform of your choice. to work with no learning curve. Some enterprises that need a CAD application Windows has traditionally been the operating have problems finding affordable software that system adopted by the industry, but there are delivers the features that they need to get the pockets of dedicated macOS users. With that in job done. While there are several budget- mind, CorelCAD is optimized for both priced alternatives, many lack critical tools or platforms — and at a fraction of the price of use a format that impedes collaboration and other CAD software available for macOS. -

20 Annual Report 20
2020 Annual Report GUIDING PRINCIPLES FOR FAIRFAX FINANCIAL HOLDINGS LIMITED OBJECTIVES: 1) We expect to compound our mark-to-market book value per share over the long term by 15% annually by running Fairfax and its subsidiaries for the long term benefit of customers, employees, shareholders and the communities where we operate – at the expense of short term profits if necessary. 2) Our focus is long term growth in book value per share and not quarterly earnings. We plan to grow through internal means as well as through friendly acquisitions. 3) We always want to be soundly financed. 4) We provide complete disclosure annually to our shareholders. STRUCTURE: 1) Our companies are decentralized and run by the presidents except for performance evaluation, succession planning, acquisitions, financing and investments, which are done by or with Fairfax. Investing will always be conducted based on a long term value-oriented philosophy. Cooperation among companies is encouraged to the benefit of Fairfax in total. 2) Complete and open communication between Fairfax and subsidiaries is an essential requirement at Fairfax. 3) Share ownership and large incentives are encouraged across the Group. 4) Fairfax will always be a very small holding company and not an operating company. VALUES: 1) Honesty and integrity are essential in all our relationships and will never be compromised. 2) We are results oriented – not political. 3) We are team players – no ‘‘egos’’. A confrontational style is not appropriate. We value loyalty – to Fairfax and our colleagues. 4) We are hard working but not at the expense of our families. 5) We always look at opportunities but emphasize downside protection and look for ways to minimize loss of capital. -

ARC Resources Q1 2017 Book
FIRST QUARTER REPORT 20 FOCUSED CORPORATE PROFILE ARC Resources Ltd. (“ARC”) is a Canadian oil and gas TABLE OF producer committed to delivering strong operational CONTENTS and financial performance and upholding values of Financial & Operational Highlights 1 operational excellence and News Release 2 responsible development. Management’s Discussion & Analysis 14 With operations in western Financial Statements 55 Canada, ARC’s portfolio is made up of resource-rich properties that provide near and long-term investment opportunities. ARC pays a monthly dividend to shareholders and its common shares trade on the Toronto Stock Exchange under the symbol ARX. FINANCIAL AND OPERATING HIGHLIGHTS Three Months Ended December 31, 2016 March 31, 2017 March 31, 2016 FINANCIAL (Cdn$ millions, except per share and boe amounts) Net income 167.0 142.5 64.1 Per share (1) 0.47 0.40 0.18 Funds from operations (2) 188.5 177.2 150.1 Per share (1) 0.53 0.50 0.43 Dividends 52.9 53.1 69.9 Per share (1) 0.15 0.15 0.20 Capital expenditures, before land and net property acquisitions (dispositions) 159.2 255.2 59.1 Total capital expenditures, including land and net property acquisitions (dispositions) (525.6) 260.6 74.2 Net debt outstanding (3) 356.5 501.4 868.4 Shares outstanding, weighted average diluted 353.5 353.7 348.9 Shares outstanding, end of period 353.3 353.4 349.8 OPERATING Production Crude oil (bbl/d) 29,885 24,030 34,852 Condensate (bbl/d) 3,767 4,504 3,442 Natural gas (MMcf/d) 478.4 496.2 489.7 NGLs (bbl/d) 4,220 3,893 4,319 Total (boe/d) (4) 117,611 -

Schedule 14A Information
SCHEDULE 14A INFORMATION Proxy Statement Pursuant to Section 14(a) of the Securities Exchange Act of 1934 Filed by the Registrant x Filed by a party other than the registrant Check the appropriate box: Preliminary proxy statement Confidential, for use of the Commission only (as permitted by Rule 14a-6(e)(2)) x Definitive proxy statement Definitive additional materials The Allstate Corporation (Name of Registrant as Specified In Its Charter) N/A (Name of Person(s) Filing Proxy Statement if other than the Registrant) Payment of filing fee (check the appropriate box): Soliciting material pursuant to Rule 14a-11(c) or Rule 14a-12 x No fee required. Fee computed on table below per Exchange Act Rules 14a-6(i)(1) and 0-11 (1) Title of each class of securities to which transaction applies: (2) Aggregate number of securities to which transaction applies: (3) Per unit price or other underlying value of transaction computed pursuant to Exchange Act Rule 0-11 (set forth the amount on which the filing fee is calculated and state how it was determined): (4) Proposed maximum aggregate value of transaction: (5) Total fee paid: Fee paid previously with preliminary materials. Check box if any part of the fee is offset as provided by Exchange Act Rule 0-11(a)(2) and identify the filing for which the offsetting fee was paid previously. Identify the previous filing by registration statement number, or the form or schedule and the date of its filing. (1) Amount previously paid: (2) Form, Schedule or Registration Statement No.: (3) Filing party: (4) Date filed: THE ALLSTATE CORPORATION 2775 Sanders Road Northbrook, Illinois 60062-6127 March 27, 2000 Notice of Annual Meeting and Proxy Statement Dear Stockholder: You are invited to attend Allstate’s 2000 annual meeting of stockholders to be held on Thursday, May 18, 2000.