Discovering Genetic Interactions Bridging Pathways in Genome-Wide Association Studies
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

(12) United States Patent (10) Patent No.: US 7,592,444 B2 Khvorova Et Al
USOO7592444B2 (12) United States Patent (10) Patent No.: US 7,592,444 B2 KhVOrOVa et al. (45) Date of Patent: Sep. 22, 2009 (54) SIRNA TARGETING MYELOID CELL 2003/0228597 A1 12/2003 COWSert LEUKEMIA SEQUENCE 1 2004/OO29275 A1 2/2004 Brown et al. 2004.00541.55 A1 3, 2004 Woolf (75) Inventors: Anastasia Khvorova, Boulder, CO 2004-0063654. A 42004 Davis et al. (US); Angela Reynolds, Conifer, CO S.S. A. 3. Singhofer (US);O O Devin Leake, Denver, CO (US); 2004/O180357 A1 9, 2004 eich William Marshall, Boulder, CO (US); 2004/O192629 A1 9, 2004 Xu et al. Stephen Scaringe, Lafayette, CO (US); 2004/0204380 A1 10, 2004 Ackerman Steven Read, Boulder, CO (US) 2004/0219671 A1 1 1/2004 McSwiggen 2004/024.8296 A1 12/2004 Beresford (73) Assignee: Dharmacon, Inc., Lafayette, CO (US) 2004/0248299 A1 12/2004 Jayasena 2004/0259247 A1 12, 2004 TuSchlet al. (*) Notice: Subject to any disclaimer, the term of this 2005/0048529 A1 3/2005 McSwiggen patent is extended or adjusted under 35 2005/0107328 A1 5/2005 Wyatt U.S.C. 154(b) by 0 days. 2005. O130181 A1 6/2005 McSwiggen 2005/0176O25 A1 8/2005 McSwiggen (21) Appl. No.: 12/378,164 2005, 0181382 A1 8, 2005 Zamore 2005, 0186586 A1 8, 2005 Zamore 2005/0227935 A1 10/2005 McSwiggen (22) Filed: Feb. 11, 2009 2005/0239731 A1 10/2005 McSwiggen 2005.0245475 A1 11/2005 Khvorova (65) Prior Publication Data 2006/0286575 A1 12/2006 Farrell US 2009/O1637O2A1 Jun. 25, 2009 2007/0031844 A1 2/2007 Khvorova 2007,0254.850 A1 11/2007 Lieberman Related U.S. -

Identification and Subcellular Localization of Human Rab5b, a New Member of the Ras-Related Superfamily of Gtpases
Identification and subcellular localization of human rab5b, a new member of the ras-related superfamily of GTPases. D B Wilson, M P Wilson J Clin Invest. 1992;89(3):996-1005. https://doi.org/10.1172/JCI115683. Research Article Members of the mammalian rab family of GTPases are associated with specific subcellular compartments, where these proteins are postulated to function in vesicular transport. By screening a human umbilical vein endothelial cell library with degenerate oligonucleotide probes, we have isolated a 1.6-kb cDNA clone encoding a 215-amino-acid protein belonging to the rab family of GTPases. This newly identified rab protein is 81% identical to human rab5, the canine counterpart of which has been localized to the plasma membrane and early endosomes. In light of this homology, we have named this new member of the GTPase superfamily "rab5b." Northern analysis using the rab5b cDNA as a probe revealed a 3.6-kb mRNA in a variety of cell types, including human umbilical vein endothelial cells, K562 erythroleukemia cells, U937 monoblastic cells, and HeLa cells. A fusion protein between glutathione-S-transferase (GST) and rab5b was expressed in bacteria and purified to homogeneity. The recombinant protein was shown to bind GTP and GDP. As is typical of other recombinant rab proteins, the rab5b-GST fusion protein displayed a low intrinsic rate of GTP hydrolysis (0.005/min). An antiserum to rab5b was prepared and used to determine the apparent molecular size and subcellular distribution of the protein. Western blotting with this antibody revealed a 25-kD protein in COS cells transfected with rab5b and in nontransfected HeLa cells. -

(12) Patent Application Publication (10) Pub. No.: US 2008/0132691 A1 Khvorova Et Al
US 2008O132691A1 (19) United States (12) Patent Application Publication (10) Pub. No.: US 2008/0132691 A1 KhVOrOVa et al. (43) Pub. Date: Jun. 5, 2008 (54) SIRNA TARGETING KINASE INSERT Related U.S. Application Data DOMAIN RECEPTOR (KDR) (63) Continuation-in-part of application No. 10/940,892, filed on Sep. 14, 2004, which is a continuation of (75) Inventors: Anastasia Khvorova, Boulder, CO application No. PCT/US04/14885, filed on May 12, (US); Angela Reynolds, Conifer, 2004, Continuation-in-part of application No. 10/714, CO (US); Devin Leake, Denver, 333, filed on Nov. 14, 2003. CO (US); William Marshall, (60) Provisional application No. 60/426,137, filed on Nov. Boulder, CO (US); Steven Read, 14, 2002, provisional application No. 60/502,050, Denver, CO (US); Stephen filed on Sep. 10, 2003. Scaringe, Lafayette, CO (US) Publication Classification Correspondence Address: (51) Int. C. KALOW & SPRINGUT LLP C7H 2L/02 (2006.01) 488 MADISONAVENUE, 19TH FLOOR (52) U.S. Cl. ....................................................... 536/24.5 NEW YORK, NY 10022 (57) ABSTRACT Efficient sequence specific gene silencing is possible through (73) Assignee: DHARMACON, INC., Lafayette, the use of siRNA technology. By selecting particular siRNAs CO (US) by rational design, one can maximize the generation of an effective gene silencing reagent, as well as methods for (21) Appl. No.: 11/978,107 silencing genes. Methods, compositions, and kits generated through rational design of siRNAS are disclosed including (22) Filed: Oct. 26, 2007 those directed to nucleotide sequences for KDR. s S & 3 & SSSSSSSSSSS k kD CHC & 17O CLCa H EEA 1-> k O-Actinin-> --, -er is a set sat -100 DynII-> .. -

Evidence for Two Independent Associations with Type 1 Diabetes at the 12Q13 Locus
Genes and Immunity (2012) 13, 66–70 & 2012 Macmillan Publishers Limited All rights reserved 1466-4879/12 www.nature.com/gene ORIGINAL ARTICLE Evidence for two independent associations with type 1 diabetes at the 12q13 locus KL Keene1,2, AR Quinlan1,2,3, X Hou2,3, IM Hall1, JC Mychaleckyj2,3, S Onengut-Gumuscu2,4 and P Concannon1,2 1Department of Biochemistry and Molecular Genetics, UVA School of Medicine, University of Virginia, Charlottesville, VA, USA; 2Center for Public Health Genomics, UVA School of Medicine, University of Virginia, Charlottesville, VA, USA; 3Department of Public Health Sciences, UVA School of Medicine, University of Virginia, Charlottesville, VA, USA and 4Division of Endocrinology and Metabolism, UVA School of Medicine, University of Virginia, Charlottesville, VA, USA Genome-wide association studies have identified associations between type 1 diabetes and single-nucleotide polymorphisms (SNPs) at chromosome 12q13, surrounding the gene ERBB3. Our objective was to fine map this region to further localize causative variants. Re-sequencing identified more than 100 putative SNPs in an 80-kb region at 12q13. By genotyping 42 SNPs, spanning B214 kb, in 382 affected sibling pair type 1 diabetes families, we were able to genotype or tag 67 common SNPs (MAFX0.05) identified from HapMap CEU data and CEU data from the 1000 Genomes Project, plus additional rare coding variants identified from our re-sequencing efforts. In all, 15 SNPs provided nominal evidence for association (Pp0.05), with type 1 diabetes. The most significant associations were observed with rs2271189 (P ¼ 4.22 Â 10À5), located in exon 27 of the ERBB3 gene, and an intergenic SNP rs11171747 (P ¼ 1.70 Â 10À4). -

Genome-Wide Association Study Reveals First Locus for Anorexia Nervosa and Metabolic Correlations
bioRxiv preprint doi: https://doi.org/10.1101/088815; this version posted December 6, 2016. The copyright holder for this preprint (which was not certified by peer review) is the author/funder, who has granted bioRxiv a license to display the preprint in perpetuity. It is made available under aCC-BY-NC-ND 4.0 International license. Genome-Wide Association Study Reveals First Locus for Anorexia Nervosa and Metabolic Correlations Authors Duncan, E.L.* ... 210 additional authors Thornton, L.M. Hinney, A. Daly, M.J. Sullivan, P.F. Zeggini, E. Breen, G. Bulik, C.M.* * Corresponding authors Abstract Anorexia nervosa (AN) is a serious eating disorder characterized by restriction of energy intake relative to requirements, resulting in abnormally low body weight. It has a lifetime prevalence of approximately 1%, disproportionately affects females1,2, and has no well replicated evidence of effective pharmacological or psychological treatments despite high morbidity and mortality2. Twin studies support a genetic basis for the observed aggregation of AN in families3, with heritability estimates of 48%-74%4. Although initial genome-wide association studies (GWASs) were underpowered5,6, evidence suggested that signals for AN would be detected with increased power5. We present a GWAS of 3,495 AN cases and 10,982 controls with one genome-wide significant locus (index variant rs4622308, p=4.3x10-9) in a region (chr12:56,372,585- % 56,482,185) which includes six genes. The SNP-chip heritability (h"#$) of AN from these data is 0.20 (SE=0.02), suggesting that a substantial fraction of the twin-based heritability stems from common genetic variation. -

Genome-Wide Association Study Reveals First Locus for Anorexia Nervosa and Metabolic Correlations
HHS Public Access Author manuscript Author ManuscriptAuthor Manuscript Author Am J Psychiatry Manuscript Author . Author Manuscript Author manuscript; available in PMC 2018 September 01. Published in final edited form as: Am J Psychiatry. 2017 September 01; 174(9): 850–858. doi:10.1176/appi.ajp.2017.16121402. Genome-Wide Association Study Reveals First Locus for Anorexia Nervosa and Metabolic Correlations Laramie Duncan, PhD, Zeynep Yilmaz, PhD, Raymond Walters, PhD, Jackie Goldstein, PhD, Verneri Anttila, PhD, Brendan Bulik-Sullivan, PhD, Stephan Ripke, MD, PhD, Eating Disorders Working Group of the Psychiatric Genomics Consortium, Laura Thornton, PhD, Anke Hinney, PhD, Mark Daly, PhD, Patrick Sullivan, MD, FRANZCP, Eleftheria Zeggini, PhD, Gerome Breen, PhD, and Cynthia Bulik, PhD Abstract Objective—To conduct a genome-wide association study (GWAS) of anorexia nervosa and to calculate genetic correlations with a series of psychiatric, educational, and metabolic phenotypes. Method—Following uniform quality control and imputation using the 1000 Genomes Project (phase 3) in 12 case-control cohorts comprising 3,495 anorexia nervosa cases and 10,982 controls, we performed standard association analysis followed by a meta-analysis across cohorts. Linkage disequilibrium score regression (LDSC) was used to calculate genome-wide common variant heritability [ , partitioned heritability, and genetic correlations (rg)] between anorexia nervosa and other phenotypes. Results—Results were obtained for 10,641,224 single nucleotide polymorphisms (SNPs) and insertion-deletion variants with minor allele frequency > 1% and imputation quality scores > 0.6. The of anorexia nervosa was 0.20 (SE=0.02), suggesting that a substantial fraction of the twin-based heritability arises from common genetic variation. -

Significant Locus and Metabolic Genetic Correlations Revealed In
ARTICLES Significant Locus and Metabolic Genetic Correlations Revealed in Genome-Wide Association Study of Anorexia Nervosa Laramie Duncan, Ph.D., Zeynep Yilmaz, Ph.D., Helena Gaspar, Ph.D., Raymond Walters, Ph.D., Jackie Goldstein, Ph.D., Verneri Anttila, Ph.D., Brendan Bulik-Sullivan, Ph.D., Stephan Ripke, M.D., Ph.D., Eating Disorders Working Group of the Psychiatric Genomics Consortium, Laura Thornton, Ph.D., Anke Hinney, Ph.D., MarkDaly,Ph.D.,PatrickF.Sullivan,M.D.,F.R.A.N.Z.C.P.,EleftheriaZeggini,Ph.D.,GeromeBreen,Ph.D., Cynthia M. Bulik, Ph.D. Objective: The authors conducted a genome-wide associ- fraction of the twin-based heritability arises from common ation study of anorexia nervosa and calculated genetic genetic variation. The authors identified one genome-wide correlations with a series of psychiatric, educational, and significant locus on chromosome 12 (rs4622308) in a region metabolic phenotypes. harboring a previously reported type 1 diabetes and auto- immune disorder locus. Significant positive genetic cor- Method: Following uniform quality control and imputation relations were observed between anorexia nervosa and procedures using the 1000 Genomes Project (phase 3) schizophrenia, neuroticism, educational attainment, and in 12 case-control cohorts comprising 3,495 anorexia high-density lipoprotein cholesterol, and significant negative nervosa cases and 10,982 controls, the authors performed genetic correlations were observed between anorexia standard association analysis followed by a meta-analysis nervosa and body mass index, insulin, glucose, and lipid across cohorts. Linkage disequilibrium score regression phenotypes. was used to calculate genome-wide common variant heritability (single-nucleotide polymorphism [SNP]-based Conclusions: Anorexia nervosa is a complex heritable phe- 2 heritability [h SNP]), partitioned heritability, and genetic notype for which this study has uncovered the first genome- correlations [rg]) between anorexia nervosa and 159 other wide significant locus. -
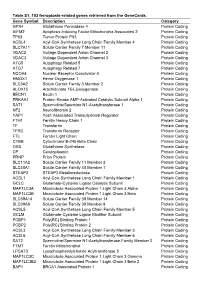
Table S1. 103 Ferroptosis-Related Genes Retrieved from the Genecards
Table S1. 103 ferroptosis-related genes retrieved from the GeneCards. Gene Symbol Description Category GPX4 Glutathione Peroxidase 4 Protein Coding AIFM2 Apoptosis Inducing Factor Mitochondria Associated 2 Protein Coding TP53 Tumor Protein P53 Protein Coding ACSL4 Acyl-CoA Synthetase Long Chain Family Member 4 Protein Coding SLC7A11 Solute Carrier Family 7 Member 11 Protein Coding VDAC2 Voltage Dependent Anion Channel 2 Protein Coding VDAC3 Voltage Dependent Anion Channel 3 Protein Coding ATG5 Autophagy Related 5 Protein Coding ATG7 Autophagy Related 7 Protein Coding NCOA4 Nuclear Receptor Coactivator 4 Protein Coding HMOX1 Heme Oxygenase 1 Protein Coding SLC3A2 Solute Carrier Family 3 Member 2 Protein Coding ALOX15 Arachidonate 15-Lipoxygenase Protein Coding BECN1 Beclin 1 Protein Coding PRKAA1 Protein Kinase AMP-Activated Catalytic Subunit Alpha 1 Protein Coding SAT1 Spermidine/Spermine N1-Acetyltransferase 1 Protein Coding NF2 Neurofibromin 2 Protein Coding YAP1 Yes1 Associated Transcriptional Regulator Protein Coding FTH1 Ferritin Heavy Chain 1 Protein Coding TF Transferrin Protein Coding TFRC Transferrin Receptor Protein Coding FTL Ferritin Light Chain Protein Coding CYBB Cytochrome B-245 Beta Chain Protein Coding GSS Glutathione Synthetase Protein Coding CP Ceruloplasmin Protein Coding PRNP Prion Protein Protein Coding SLC11A2 Solute Carrier Family 11 Member 2 Protein Coding SLC40A1 Solute Carrier Family 40 Member 1 Protein Coding STEAP3 STEAP3 Metalloreductase Protein Coding ACSL1 Acyl-CoA Synthetase Long Chain Family Member 1 Protein -

Primepcr™Assay Validation Report
PrimePCR™Assay Validation Report Gene Information Gene Name ras-related protein Rab-5B Gene Symbol Rab5b Organism Rat Gene Summary Description Not Available Gene Aliases Not Available RefSeq Accession No. Not Available UniGene ID Rn.3305 Ensembl Gene ID ENSRNOG00000006130 Entrez Gene ID 288779 Assay Information Unique Assay ID qRnoCEP0026345 Assay Type Probe - Validation information is for the primer pair using SYBR® Green detection Detected Coding Transcript(s) ENSRNOT00000061878 Amplicon Context Sequence TAAGTGGAAGAACCTAAGTTGGGTCCTTGAGAATCTTGGCTTCATGGATTCCTCA GCTGGAATACAAGTCAGTGTCTAAGCCAAAGGGGCAGAAAGGCTCAACTCTAGG CTACTGTGGTCTTT Amplicon Length (bp) 93 Chromosome Location 7:3077784-3077906 Assay Design Exonic Purification Desalted Validation Results Efficiency (%) 98 R2 0.9986 cDNA Cq 20.03 cDNA Tm (Celsius) 81.5 gDNA Cq 25.21 Specificity (%) 100 Information to assist with data interpretation is provided at the end of this report. Page 1/4 PrimePCR™Assay Validation Report Rab5b, Rat Amplification Plot Amplification of cDNA generated from 25 ng of universal reference RNA Melt Peak Melt curve analysis of above amplification Standard Curve Standard curve generated using 20 million copies of template diluted 10-fold to 20 copies Page 2/4 PrimePCR™Assay Validation Report Products used to generate validation data Real-Time PCR Instrument CFX384 Real-Time PCR Detection System Reverse Transcription Reagent iScript™ Advanced cDNA Synthesis Kit for RT-qPCR Real-Time PCR Supermix SsoAdvanced™ SYBR® Green Supermix Experimental Sample qPCR Reference Total RNA Data Interpretation Unique Assay ID This is a unique identifier that can be used to identify the assay in the literature and online. Detected Coding Transcript(s) This is a list of the Ensembl transcript ID(s) that this assay will detect. -

Autosomal Dominant Axonal Charcot
193 LETTER TO JMG J Med Genet: first published as 10.1136/jmg.2003.012633 on 1 March 2004. Downloaded from Autosomal dominant axonal Charcot-Marie-Tooth disease type 2 (CMT2G) maps to chromosome 12q12–q13.3 E Nelis, J Berciano, N Verpoorten, K Coen, I Dierick, V Van Gerwen, O Combarros, P De Jonghe, V Timmerman ............................................................................................................................... J Med Genet 2004;41:193–197. doi: 10.1136/jmg.2003.012633 harcot-Marie-Tooth (CMT) disease is a clinically and genetically heterogeneous group of disorders that Key points Cinvolve the peripheral nervous system.1 It is charac- terised by progressive distal neurogenic muscular atrophy N Charcot-Marie-Tooth (CMT) neuropathies are hetero- and weakness that initially affects the peroneal muscles and geneous clinically and genetically. For the auto- later the hands. Charcot-Marie-Tooth disease type 1 (CMT1), somal dominant axonal type of CMT or CMT type 2 also called hereditary motor and sensory neuropathy type I (CMT2), six loci and four genes have been reported. (HMSN I), is a dominantly inherited demyelinating neuro- N A genomewide scan was performed in a Spanish pathy characterised by reduced nerve conduction velocities family with autosomal dominant CMT2 not linked to the (NCV) (motor median NCV ,38 m/s). Charcot-Marie-Tooth known CMT2 loci and conclusive linkage with a disease type 2 (CMT) 2, or HMSN II, is a dominantly chromosome 12q13.13 marker was obtained. Fine inherited axonal neuropathy characterised by normal or mapping localised this novel CMT2 locus to a 13.2 Mb slightly reduced NCV. Both autosomal dominant CMT1 and autosomal dominant CMT2 are genetically heterogeneous, (12.8 cM) interval between D12S1663 and with five and six loci, respectively.2 Most patients with CMT1 D12S1644 at 12q12–q13.3. -

The Regulation of Rab5 by Phosphatidylinositol 3′-Kinase
THE REGULATION OF RAB5 BY PHOSPHATIDYLINOSITOL 3′-KINASE A Thesis Submitted to the College of Graduate Studies and Research in Partial Fulfillment of the Requirements of the Degree of Master of Science in the Department of Biochemistry University of Saskatchewan Saskatoon by Dielle Detillieux © Copyright Dielle Detillieux, December 2012. All rights reserved. PERMISSION TO USE In presenting this thesis in partial fulfillment of the requirements for a Postgraduate degree from the University of Saskatchewan, I agree that the Libraries of this University may make it freely available for inspection. I further agree that permission for copying of this thesis in any manner, in whole or in part, for scholarly purposes may be granted by the professor or professors who supervised my thesis work or, in their absence, by the Head of the Department or the Dean of the College under which this thesis work was done. It is understood that any copying or publication or use of this thesis or parts thereof for financial gain shall not be allowed without my written permission. It is also understood that due recognition shall be given to me and to the University of Saskatchewan in any scholarly use which may be made of any material in my thesis. Request for permission to copy or to make other use of materials in this thesis in whole or in part should be addressed to: Dr. Deborah H. Anderson Saskatchewan Cancer Agency Cancer Research Unit 20 Campus Drive University of Saskatchewan Saskatoon, SK S7N 4H4 i ABSTRACT Rab5 (Ras-related in brain) and Rab4 are small monomeric GTPases that mediate the intracellular trafficking of endocytosed growth factor receptors. -

Membranes of Human Neutrophils Secretory Vesicle Membranes And
Comparison of Proteins Expressed on Secretory Vesicle Membranes and Plasma Membranes of Human Neutrophils This information is current as Silvia M. Uriarte, David W. Powell, Gregory C. Luerman, of September 25, 2021. Michael L. Merchant, Timothy D. Cummins, Neelakshi R. Jog, Richard A. Ward and Kenneth R. McLeish J Immunol 2008; 180:5575-5581; ; doi: 10.4049/jimmunol.180.8.5575 http://www.jimmunol.org/content/180/8/5575 Downloaded from Supplementary http://www.jimmunol.org/content/suppl/2008/04/01/180.8.5575.DC1 Material http://www.jimmunol.org/ References This article cites 44 articles, 25 of which you can access for free at: http://www.jimmunol.org/content/180/8/5575.full#ref-list-1 Why The JI? Submit online. • Rapid Reviews! 30 days* from submission to initial decision by guest on September 25, 2021 • No Triage! Every submission reviewed by practicing scientists • Fast Publication! 4 weeks from acceptance to publication *average Subscription Information about subscribing to The Journal of Immunology is online at: http://jimmunol.org/subscription Permissions Submit copyright permission requests at: http://www.aai.org/About/Publications/JI/copyright.html Email Alerts Receive free email-alerts when new articles cite this article. Sign up at: http://jimmunol.org/alerts The Journal of Immunology is published twice each month by The American Association of Immunologists, Inc., 1451 Rockville Pike, Suite 650, Rockville, MD 20852 Copyright © 2008 by The American Association of Immunologists All rights reserved. Print ISSN: 0022-1767 Online ISSN: 1550-6606. The Journal of Immunology Comparison of Proteins Expressed on Secretory Vesicle Membranes and Plasma Membranes of Human Neutrophils1 Silvia M.