DOCSLIB.ORG

Cornish-Fisher Expansion on Estimation and Forecasting Models of Stock Return Volatility

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Cornish-Fisher Expansion on Estimation and Forecasting Models of Stock Return Volatility Cornish-Fisher Expansion on Estimation and Forecasting Models of Stock Return Volatility Dr. Leila Y. Calderon Financial Management Department, De La Salle University-Manila INTRODUCTION The ability to forecast financial market volatility is important for portfolio selection and asset management. However, predicting volatility is a challenge and there are different volatility models available to choose from. Understanding the stock return volatility will result into better investment strategies. In most cases, the widespread popularity of mean-variance analysis is due to the fact that it is very simple and powerful. Most of the theoretical and empirical work on portfolio selection and the pricing of financial assets use the mean-variance analysis. Many investors limit their decisions on the mean-variance analysis as a simple exercise to risk-return tradeoff. The variance is usually unconditional as computed by the standard deviation of the sample period. However, it has been proven by studies that stock return volatility is time varying as was shown by Autoregressive Conditional Heteroscedasticity (ARCH) (Engle, 1982). DLSU Business & Economics Review Volume 13 No.1 2001-2002 22 CORNISH-FISHER EXPANSION The daily volume and prices of the ten selected index issues and that of the daily Philippine Stock Exchange Composite Index (Phisix) from 01 April 1994 - 31 March 1999 were taken from the research department of the Philippine Stock Exchange (PSE). During this period, the One-Price One Market exchange has been achieved through the successful link-up of the two trading floors, PSE-Ayala and PSE-Tektite (Fact Book, 1996). At present, the Phisix has 30 constituent stocks; however, this study is limited only to ten stocks included in the Phisix. Selection of the ten issues was done randomly; however, all the stocks selected were included in all the recompositions of the Phisix for the years 1994, 1996, and 1998. This means that these stocks have satisfactorily complied with the requirements of the PSE to be included in the Phisix (Appendix A). In the estimation and forecasting models of stock return volatility, focus was only on the closing prices. The closing prices were used because investors and/or fund managers look at these prices to determine their positions. At times, they drive the market to close at a certain level by entering the market a few minutes before the close of the trading period. It is noted that investors may not have the time to monitor the market at all instances, thus forcing them to make investment decisions on closing prices. The daily returns (R,) for the Phisix and the selected issues were computed as follows: R, = In (P,/ P ,_, ) (1.1) Where P, today's closing price P ,_, previous closing price In is the natural logarithm Stock return volatility was determined through the computation of the standard deviation. 2 <J = _ {I(r. -r) (1.2) V · n -1 where N is the number of observations r1 is each observation r is the average observation r.v summation sign which means that we add up over all observations DLSU Business & Economics Review Volume 13 No.1 2001-2002 Leila Y. C&lderon 23 As was mentioned earlier, stock return volatility as measured by the unconditional standard deviation is time-varying. Thus, Alexander (1998) suggests the "Generalized Autoregressive Conditional Heteroscedasticity (GARCH) to estimate and forecast volatility. "Generalized," because it is a general class of ARCH model; "Autoregressive," the variances generated by ARCH models involve regression on their own past; and "Conditional Heteroscedastic," means changing variance or volatility clustering. In this GARCH model, there are two equations: (1) the conditional mean and (2) the conditional variance equations. The parameters in both equations are estimated simultaneously, using maximum likelihood estimation. The standard input for a GARCH model for financial market volatility is a series of daily returns, r,, the dependent variable. It is important to note the difference between an estimate and a forecast. In general, historical data is used to estimate volatility or correlation, and the estimate is then used to construct the forecasts. In this case, the GARCH volatility estimates are different from the forecasts. GARCH forecasts of volatility of any maturity can be computed in a simple iterative manner. Put: (1.3) Assuming returns have no autocorrelation, the GARCH forecasts of variance of h-day returns is h a",,,= I cf,,, (1.4) i=1 and the GARCH h-day volatility forecast is 100cr,, • v'250%, assuming 250 trading days per year. An important element of the ARCH model is that it more readily explains ''fat tailed" and leptokurtic distributions of asset price changes. The major applications of ARCH models, have, to date, been modelling correlations between assets and forecasting volatility (Das, 1998). The GARCH model is an infinite order ARCH model. One member of the family of ARCH processes, GARCH (1, 1) has been especially popular because of its parsimony. In this study, the GARCH (1, 1) is used to estimate volatility of the index issues' stock returns. DLSU Business & Economics Review Volunu 13 No.1 2001-2002 24 CORNISH-FISHER EXPANSION Alexander (1996) considered the unconditional standard deviation over a long data period as a benchmark against which to test different volatility forecasting models. In this study, the unconditional standard deviation will be the one used to compare against the different volatility forecasting models. The test of forecasting power lies in out-of-sample (usually post-sample) predictive tests. A certain amount of historic data is withheld from the period used to construct the forecast model. The model is evaluated through the use of two forecast error statistics, namely: root mean squared error and mean absolute error. The smaller the error, the better the forecasting ability of that model according to that criterion. (Take directly from Eviews 3 User's Guide). As mentioned earlier the unconditional standard deviation will be used to compare against the forecasts of the other volatility models. In most cases, the widespread popularity of mean­ variance analysis is due to the fact that it is very simple and powerful. Most of the theoretical and empirical work on portfolio selection and the pricing of financial assets use the mean-variance analysis. However, an inadequacy of relying on the variance alone is that it fails To measure the symmetrical treatment of gains or loses, if these deviations are pleasant or unpleasant surprises. These surprises need not be evenly distributed, however. There may be a large probability of a slightly above average return and a small chance of a catastrophic loss, or there might be a large probability of a small loss and a small chance of a bonanza. To capture this asymmetry, skewness may be a rational explanation. (Reid, 1991 ). The asymmetry of the distribution is called the skewness, or the third central moment, given by n M' = l:Pr(s) [r(s)-E(r)]' (1.5) S=1 where s =return Pr = probability E(r) = expected value of return Cubing the deviations from expected value preserves their signs, which allows us to distinguish good from bad surprises. DLSU Business & Economics Review Volume 13 No.1 2001-2002 Leila Y. Calderon 25 Because, this procedure gives greater weight to larger deviations, it causes the long tail of the distribution to dominate the measure of skewness. Positive numbers are associated with positive · skewness and hence is desirable (Bodie, Kane, Marcus , 1999). As for kurtosis, the fourth central moment, along with the variance (second moment) represent the likelihood of extreme values. Larger values for these moments indicate greater uncertainty (Bodie, Kane, Marcus , 1999). n M4 = IPr(s) [r(s)·E(r)]4 (1.6) S=1 where s =return Pr = probability E(r) = expected value of return Kurtosis is the degree of peakedness of a distribution, usually taken relative to a normal distribution. A distribution having a high peak, and having a value greater than 3 are called leptokurtic; whereas, values of Kless than 3 are platykurtic (flat-topped); and a kurtosis value of 3 is known as mesokurtlc. Most statistical problems rely in some way on approximations to densities or distribution functions derived from asymptotic theory. The central limit guarantees that for most underlying . distributions, the distribution of sample mean Y can be approximated by a normal distribution. This approximation may be improved by transforming the Y's before averaging or by incorporating an adjustment for skewness and kurtosis. In adjusting for skewness and kurtosis, the Cornish-Fisher expansion has been utilized. 2 3 3 z + (1/6) (z 1) p + (1/24) {z ·3 z ) p• (1.7) w.= 0 0 0 0 where z = probability of normal distribution at 5% 0 significance level p 3 = skewness p4 = kurtosis (source for equations: N. Reid, 1991) DLSU Business & Economics Review Volume 13 No.1 2001·2002 26 CORNISH-FISHER EXPANSION In the model, three forecasts will be made: one for the whole sample period from 04 April1994 to 31 March 1999; a 90-day in­ sample period from 18 November 1998 to 31 March 1999; and a 90-day out-of-sample per iod from 05 April 1999 to 10 August 1999. The unconditional standard deviation will be added to or subtracted from the mean to determine the forecasted stock price using the formula: x ± 1.96*s/vn (1.8) Where X - the mean of the closing prices of the stock s - unconditional standard deviation of the returns n - sample size, in this case 1,250 observations for the period 4 April1994- 31 March 1999. The forecasted stock price is based on the actual closing price of the day since under the Martingale Property, "the unconditional expectation of your winnings at any time in the future is just the amount you already hold: (Wilmott, 1998) The same procedure will be done using the mean­ unconditional standard deviation, the mean-conditional standard deviation.
Load more

Recommended publications
  • Quarterly Economic Update
    DSI Wealth Management Group Presents: QUARTERLY ECONOMIC UPDATE A review of 1Q 2014 QUOTE OF THE THE QUARTER IN BRIEF QUARTER Bulls didn’t quite trample bears in the opening quarter of 2014. The S&P 500 slid “If there is no 3.56% in January, advanced 4.31% in February and gained another 0.69% in March. struggle, there is no Still, Q1 ended with the Dow in the red YTD and only minor YTD gains for the progress.” Nasdaq, S&P and Russell 2000; the broad commodities market outperformed the stock market. Some fundamental economic indicators were unimpressive during the – Frederick Douglass quarter, and analysts wondered if a ferocious winter was partly to blame. The Federal Reserve kept tapering QE3 as Ben Bernanke handed the reins to Janet QUARTERLY TIP Yellen. Unrest and currency problems hit some key emerging-market economies. Given the choice Home prices kept rising as home sales leveled off. Wall Street hoped the year 1 between a great wouldn’t mimic the quarter. lifestyle today and financial freedom DOMESTIC ECONOMIC HEALTH tomorrow, many The quarter ended with a major jump in consumer confidence. The Conference people opt to live for Board’s index reached 82.3 in March, up 4.0 points in a month. Consumer spending today – but no one improved too, rising 0.2% in January and 0.3% in February. (In a contrasting note, becomes wealthy by the University of Michigan’s consumer sentiment index slipped 2.5 points across the spending or living on quarter to a final March mark of 80.0.)2,3 margin.
    [Show full text]
  • Uncovered Equity “Disparity” in Emerging Markets
    City Research Online City, University of London Institutional Repository Citation: Fuertes, A-M. ORCID: 0000-0001-6468-9845, Phylaktis, K. ORCID: 0000-0001- 9392-1682 and Yan, C. (2019). Uncovered Equity “Disparity” in Emerging Markets. Journal of International Money and Finance, doi: 10.1016/j.jimonfin.2019.102066 This is the accepted version of the paper. This version of the publication may differ from the final published version. Permanent repository link: https://openaccess.city.ac.uk/id/eprint/22585/ Link to published version: http://dx.doi.org/10.1016/j.jimonfin.2019.102066 Copyright: City Research Online aims to make research outputs of City, University of London available to a wider audience. Copyright and Moral Rights remain with the author(s) and/or copyright holders. URLs from City Research Online may be freely distributed and linked to. Reuse: Copies of full items can be used for personal research or study, educational, or not-for-profit purposes without prior permission or charge. Provided that the authors, title and full bibliographic details are credited, a hyperlink and/or URL is given for the original metadata page and the content is not changed in any way. City Research Online: http://openaccess.city.ac.uk/ [email protected] Journal of International Money & Finance, forthcoming Uncovered Equity “Disparity” in Emerging Markets Ana-Maria Fuertes, Kate Phylaktis*, Cheng Yan 11th July 2019 The portfolio-rebalancing theory of Hau and Rey (2006) yields the uncovered equity parity (UEP) prediction that local-currency equity return appreciation is offset by currency depreciation. Vector autoregressive model estimation and tests for eight Asian emerging markets using daily data reveal instead a positive nexus between equity returns and currency returns.
    [Show full text]
  • Securities and Exchange Commission Sec Form 20-Is
    CR03839-2015 SECURITIES AND EXCHANGE COMMISSION SEC FORM 20-IS INFORMATION STATEMENT PURSUANT TO SECTION 17.1(b) OF THE SECURITIES REGULATION CODE 1. Check the appropriate box: Preliminary Information Statement Definitive Information Statement 2. Name of Registrant as specified in its charter ROBINSONS RETAIL HOLDINGS, INC. 3. Province, country or other jurisdiction of incorporation or organization Philippines 4. SEC Identification Number A200201756 5. BIR Tax Identification Code 216-303-212-000 6. Address of principal office 110 E. Rodriguez, Jr. Avenue, Bagumbayan, Quezon City, Metro Manila Postal Code 1110 7. Registrant's telephone number, including area code (632) 635-0751 8. Date, time and place of the meeting of security holders July 16, 2015, 4:00 P.M., Ruby Ballroom, Crowne Plaza Manila Galleria, Ortigas Avenue corner Asian Development Bank Avenue, Quezon City, Metro Manila 9. Approximate date on which the Information Statement is first to be sent or given to security holders Jun 18, 2015 10. In case of Proxy Solicitations: Name of Person Filing the Statement/Solicitor N/A Address and Telephone No. N/A 11. Securities registered pursuant to Sections 8 and 12 of the Code or Sections 4 and 8 of the RSA (information on number of shares and amount of debt is applicable only to corporate registrants): Title of Each Class Number of Shares of Common Stock Outstanding and Amount of Debt Outstanding Common shares 1,385,000,000 13. Are any or all of registrant's securities listed on a Stock Exchange? Yes No If yes, state the name of such stock exchange and the classes of securities listed therein: Robinsons Retail Holdings, Inc.’s common stock is listed on the Philippine Stock Exchange.
    [Show full text]
  • CHAPTER 1 INTRODUCTION 1.1. Object Overview 1.1.1 Indonesia
    CHAPTER 1 INTRODUCTION 1.1. Object Overview 1.1.1 Indonesia Composite Stock Price Index The Composite Stock Price Index is usually abbreviated as IHSG in English is also commonly called the Indonesia Composite Index, ICI, or IDX Composite. The definition of a Composite Stock Price Index (CSPI) or the meaning of JCI is one of several stock market indices (stock markets) used by the Indonesia Stock Exchange (BEI; formerly the Jakarta Stock Exchange (BEJ). The IHSG was first introduced on April 1, 1983, the function of the stock price index acts as an indicator that reflects the share price movements in the JSX in general (Oktarina, 2016). 1.1.2 Thailand Composite Stock Price Index The SET Index is a Thailand composite stock market index which is calculated from the prices of all common stocks (including unit trusts of property funds) on the main board of the Stock Exchange of Thailand (SET), except for stocks that have been suspended for more than one year. It is a market capitalization- weighted price Index which compares the current market value of all listed common shares with its value on the base date of April 30, 1975, which was when the Index was established and set at 100 point/ The SET Index calculation is adjusted in line with modifications in the values of stocks resulting from changes in the number of stocks due to various events, e.g., public offerings, exercised warrants, or conversions of preferred to common shares, in order to eliminate all effects other than price movements from the Index (Sutheebanjard and Premchaiswadi, 2010).
    [Show full text]
  • Durations of Trade in the Philippine Stock Market: an Application of the Markov-Switching Multi-Fractal Duration (Msmd) Model
    DURATIONS OF TRADE IN THE PHILIPPINE STOCK MARKET: AN APPLICATION OF THE MARKOV-SWITCHING MULTI-FRACTAL DURATION (MSMD) MODEL Jennifer E. Hinlo1 and Agustina Tan-Cruz2 ABSTRACT This study examined the durations of trade in the Philippine Stock Market using the Markov Switching Multi-Fractal Duration (MSMD) Model using tick data from 20 frequently traded stocks in the Philippine Stock Market. Results revealed that higher duration results to lower trading intensity because of low information of traders about the stocks during the period. The lesser attention paid to the stock, the more likely that trade will not happen. The higher trading intensity is a result of shorter trade durations, this means that the interval from one trading transaction to another is smaller. The higher the trading intensity implies higher price impact of trades and faster price adjustment to new trade-related information. Information flow affects intensities but it does not trigger trading automatically because investors have limited attention, and they need to allocate attention to process all kinds of information before making a trading decision. Keywords: Markov Switching Multi-Fractal Duration (MSMD) Model, Philippine Stock Market, Trade Durations EXECUTIVE SUMMARY This study examined the durations of trade in the Philippine Stock Exchange (PSE) using the Markov Switching Multi-Fractal Duration (MSMD) Model using top twenty (20) randomly selected active firms listed in the PSE. Tick-by-tick intra-day trading of the equities in the PSE were used, from May 2 to 31, 2013, from 9:00 – 3:30pm (where the PSEI has recorded its 31st all-time high index).
    [Show full text]
  • Asia Bond Monitor—November 2016 Was Prepared by the Asianbondsonline (ABO) Team
    Asia Bond Monitor November 2016 This publication reviews recent developments in East Asian local currency bond markets along with the outlook, risks, and policy options. It covers the 10 members of the Association of Southeast Asian Nations plus the People’s Republic of China; Hong Kong, China; and the Republic of Korea. About the Asian Development Bank ADB’s vision is an Asia and Pacific region free of poverty. Its mission is to help its developing member countries reduce poverty and improve the quality of life of their people. Despite the region’s many successes, it remains home to half of the world’s extreme poor. ADB is committed to reducing poverty through inclusive economic growth, environmentally sustainable growth, and regional integration. Based in Manila, ADB is owned by 67 members, including 48 from the region. Its main instruments for helping its developing member countries are policy dialogue, loans, equity investments, guarantees, grants, and technical assistance. ASIA BOND MONITOR NOVEMBER 2016 ASIAN DEVELOPMENT BANK 6 ADB Avenue, Mandaluyong City 1550 Metro Manila, Philippines ASIAN DEVELOPMENT BANK www.adb.org The Asia Bond Monitor (ABM) is part of the Asian How to reach us: Bond Markets Initiative (ABMI), an ASEAN+3 initiative Asian Development Bank supported by the Asian Development Bank. This report Economic Research and Regional Cooperation is part of the implementation of a technical assistance Department project funded by the Investment Climate Facilitation 6 ADB Avenue, Mandaluyong City Fund of the Government of Japan under the Regional 1550 Metro Manila, Philippines Cooperation and Integration Financing Partnership Tel +63 2 632 6688 Facility.
    [Show full text]
  • The Factors Affecting Stock Market Volatility and Contagion: Thailand and South-East Asia Evidence
    The Factors Affecting Stock Market Volatility and Contagion: Thailand and South-East Asia Evidence Thesis submitted in partial fulfilment of the requirements for the degree of Doctorate of Business Administration by Paramin Khositkulporn School of Business Victoria University Melbourne February 2013 Declaration I, Paramin Khositkulporn, declare that the DBA thesis entitled “The Factors Affecting Stock Market Volatility and Contagion: Thailand and South-East Asia Evidence” is no more than 65,000 words in length including quotes and exclusive of tables, figures, appendices, bibliography, references and footnotes. This thesis contains no material that has been submitted previously, in whole or in part, for the award of any other academic degree or diploma. Except where otherwise indicated, this thesis is my own work. Paramin Khositkulporn Date ii Contents Declaration ........................................................................................................................ ii Contents ........................................................................................................................... iii List of Tables .................................................................................................................... v List of Figures ................................................................................................................. vii List of Abbreviations ..................................................................................................... viii Acknowledgements .........................................................................................................
    [Show full text]
  • Execution Copy
    EXECUTION COPY GUARANTEED SENIOR SECURED NOTES PROGRAMME issued by GOLDMAN SACHS BANK (EUROPE) PLC in respect qf which the payment and delivery obligations are guaranteedby THE GOLDMAN SACHS GROUP, INC. (the "PROGRAMME") "FINAL TERMS" DATED 1 1 AUGUST 2009 SERIES 2009-02 SENIOR SECURED FLOATING RATE NOTES, DUE II FEBRUARY 201 0 (the "SERIES") ISIN XS0443581235 Common Code 044358123 This document must be read in conjunction with the Base Prospectus and in particular, the Base Terms and Conditions of the Notes, as set out therein Full information on the Issuer, The Goldman Sachs Group Inc (the "Guarantor"), and the terms and conditions of the Notes, is only available on the basis of the combination of the Final Terms and the Base Prospectus The Base Prospectus is available for viewing at www financialregulator ie and during normal business hours at the registered office of the Issuer, and copies may be obtained from the specified office of the listing agent in Ireland The Issuer accepts responsibility for the information contained in these Final Terms. To the best of the knowledge and belief of the Issuer and the Guarantor (which have taken all reasonable care to ensure that such is the case) the information contained in the Base Prospectus, as completed and/or amended by these Final Terms in relation to the Series of Notes referred to above, is true and accurate in all material respects and, in the context of the issue of this Series, there are no other material facts the omission of which would make any statement in such information misleading Unless terms are defined herein, capitalized terrns shall have the meanings given to them in the Base Prospectus or in the indenture, between Goldman Sachs Bank (Europe) PLC, Goldman Sachs International and The Bank of New York Mellon, acting through its London Branch, dated as of 12 February 2009, as amended and restated as of 23 July 2009 (the "Indenture") There is hereby established pursuant to this Series Authorisation, a Series of Notes to be issued under the Indenture, which has the following terms.
    [Show full text]
  • Association of South-East Asian Nations-US Stock Market
    International Journal of Economics and Financial Issues ISSN: 2146-4138 available at http: www.econjournals.com International Journal of Economics and Financial Issues, 2017, 7(3), 684-705. Association of South-East Asian Nations-US Stock Market Associations in and Around US 2007-09 Financial Crisis: An Autoregressive Distributed Lag Application for Policy Implications Ranjan Dasgupta* Xavier University Bhubaneshwar, Xavier Square, Bhubaneshwar, Odisha, India. *Email: [email protected] ABSTRACT This study examines portfolio diversification and arbitrage opportunities available to international investors in 16 Asian and US stock markets by using most advanced autoregressive distributed lag methods in and around recent US sub-prime crisis of 2007-09 with selected structural breaks. Results show that in overall and during-the-crisis period these markets were co-integrated in long-run and there were not enough portfolio diversification opportunities for international investors like other sub-periods. The Indian and Chinese markets were strongest contenders among Asian and US to attract foreign inflows. In short-run, these markets show dynamic adjustments generally within 1 month which neutralizes arbitrage opportunities. Keywords: Asian and US Stock Markets, Autoregressive Distributed Lag, Co-integrations, Market Efficiency, Portfolio Diversification, US 2007-09 Crisis JEL Classifications: C32, G15 1. INTRODUCTION also suggested a positive association between market integration and informational efficiency. Dwyer and Wallace (1992) define Co-integration and linkages of international stock markets has market efficiency as the lack of arbitrage opportunities. Thus, it is been a serious proposition for the policy-makers, investors, evident that efficient markets are generally co-integrated. Also, the academicians and researchers worldwide especially post- removal of barriers between international markets would lead to liberalization in the 90s in most parts around the world.
    [Show full text]
  • PSE AR 01 Body
    Philippine Stock Exchange 2001 ANNUAL REPORT chairman’s report It was an extremely difficult period. The country was weighed down by a turbulent political crisis. The year 2001 opened with an ongoing impeachment trial of the Philippine president, accused of plunder and other offenses, which was started in the previous year. Unexpectedly, the trial was suddenly aborted followed by another peaceful people power at EDSA which forced Joseph Estrada to step down and was replaced by Gloria Macapagal Arroyo as President. Shortly thereafter, the nation saw a violent political upheaval in May. The supporters of the former President attacked the Malacañang Palace in an unsuccessful attempt to reinstate their leader. The domestic economy, already affected by the The steep decline in share prices in 2001 global economic slowdown, suffered the brunt of the resulted in a 27% drop in market capitalization to a political disturbances. The peso declined to P53 to $1 low of P1.9 trillion in October from a high of P2.6 – its lowest for the year. The economic problem was trillion in January. aggravated by the September 11 terrorist attacks in Despite last year’s gloomy condition in our stock the United States which heavily affected our export market, the PSE was able to launch the Small and industry and further depressed our currency. Medium Enterprise (SME) Board with the listing of the As a result of the weak economy and the political first SME company that conducted an IPO, the SQL* turmoil, our stock market, already saddled by the Wizard, Inc. Fortunately, two more companies were stringent provisions of the Securities Regulation Code, listed before the year ended, namely Primex recorded its worst performance in years.
    [Show full text]
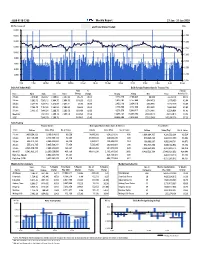
  • Weekly Report 27 Jan - 31 Jan 2020
    ISSN 0118-1785 Weekly Report 27 Jan - 31 Jan 2020 Mil Php (truncated) and Total Value Traded PSEi 18,000 16,000 8,700 14,000 8,200 12,000 7,700 10,000 7,200 8,000 6,700 6,000 6,200 4,000 2,000 5,700 - 5,200 1-Feb 1-Mar 29-Mar 26-Apr 24-May 21-Jun 19-Jul 16-Aug 13-Sep 11-Oct 8-Nov 6-Dec 3-Jan 31-Jan Daily PSE Index (PSEi) Daily Foreign Transactions (in Thousand Php) Point % Foreign Date Open High Low Close Change Change Buying Selling Net Total Activity (%) 27-Jan 7,616.90 7,624.37 7,580.67 7,587.63 (35.78) (0.47) 2,170,726 2,104,043 66,683 4,274,770 49.72 28-Jan 7,563.12 7,563.12 7,468.70 7,468.70 (118.93) (1.57) 1,613,191 2,157,664 (544,473) 3,770,855 42.44 29-Jan 7,472.53 7,472.53 7,423.69 7,462.31 (6.39) (0.09) 2,453,119 2,804,110 (350,991) 5,257,229 53.05 30-Jan 7,466.45 7,484.65 7,392.68 7,392.68 (69.63) (0.93) 2,739,509 3,252,560 (513,051) 5,992,068 54.98 31-Jan 7,413.17 7,446.26 7,200.79 7,200.79 (191.89) (2.60) 4,278,576 5,980,417 (1,701,841) 10,258,994 61.82 Week 051 7,587.63 7,200.79 7,200.79 (422.62) (5.54) 13,255,121 16,298,794 (3,043,673) 29,553,915 53.84 YTD2 7,840.70 7,200.79 (614.47) (7.86) 69,886,294 77,419,883 (7,533,589) 147,306,178 57.20 Daily Trading Regular Market Non-regular Market (Block Sales & Odd Lot) Total Market Date Volume Value (Php) No.
    [Show full text]
  • Notice of Annual Stockholders' Meeting
    SECURITIES AND EXCHANGE COMMISSION SEC FORM 20-IS Information Statement Pursuant to Section 20 of The Securities Regulation Code 1. Check the appropriate box: [] Preliminary Information Statement [ ] Definitive Information Statement 2. Name of Company as specified in its charter: Philequity PSE Index Fund, Inc. 3. Province, country or other jurisdiction of incorporation or organization: Metro Manila, Philippines 4. SEC Identification Number: A1998-16221 5. BIR Tax Identification Code: 201-884-062-000 6. Address of principal office: 15th Floor, Philippine Stock Exchange, 5th Ave. cor. 28th Street, Bonifacio Global City, Taguig City, Metro Manila 1630 7. Company’s telephone number, including area code: (632) 250-8700 8. Date, time and place of the meeting of security holders: Date : 31 August 2019 Time : 9:40 a.m. Venue : Meralco Theatre, Ortigas Avenue, Pasig City 9. Approximate date on which the Information Statement is first to be sent or given to security holders: 07 August 2019 10. Securities registered pursuant to sections 4 and 8 of the Code (information on number of shares and amount of debt is applicable only to corporate registrants): Number of shares of Title of Each Class Common Stock Outstanding Common Stock, 722,466,748 P1.00 par value (as of 31 July 2019) 11. Are any or all Company’s securities listed on a Stock Exchange? Yes [ ] No [ ] WE ARE NOT ASKING OR REQUIRING YOU TO SEND US A PROXY 1 GENERAL INFORMATION Item 1. Date, Time, and Place of Meeting of Security Holders A. Date : 31 August 2019 Time : 9:40 a.m. Venue : Meralco Theatre, Ortigas Avenue, Pasig City Mailing Address: 15th Floor, Philippine Stock Exchange, 5th Ave.
    [Show full text]