DOCSLIB.ORG

4Th International DAAAM Conference (12

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
4Th International DAAAM Conference (12 9th International DAAAM Baltic Conference "INDUSTRIAL ENGINEERING 24-26 April 2014, Tallinn, Estonia FINITE ELEMENT METHOD AND ITS USABLE APPLICATIONS IN WEAR MODELS DESIGN Sivitski, A; Põdra, P. Abstract: FEM models allow to perform Archard’s wear law, first published by more accurate calculations of contact Holm [3] and used for dimensionless wear strength and to predict the wear characters coefficient K calculation, was based on the of materials. The prognosis of material experimental observations and was initially behavior under load makes it possible to written in form: save resources and to abandon a trial-and- V F error method. The development of a FEM = K N , (1) model as well as operating with FEM s H programs is a complicated and time- consuming process. The skills of model where V is the volume wear (m3), s is simplification become more and more the sliding distance (m), FN is the normal important. The shape and the number of load (N) and H is the hardness (Pa). elements, moduli of elasticity of materials The more important wear parameter, wear and contact stiffness parameters should be depth h, is calculated by dividing both also considered. At this moment there is no sides of equation (1) by the apparent usable application for FEM models contact area: creation available for wear calculations. In this paper usable application for contact h = kps , (2) stress FEM calculations of coated bodies is offered, that can be used by engineers of where p is the normal contact pressure different areas. (Pa) over that particular discrete region, s Key words: Wear of materials; Coatings; is sliding distance (m), k = K/H is the FEM Hertz contact and Wear models dimensional wear coefficient (Pa-1). The Hertz elastic contact theory [4] has 1. INTRODUCTION widely been used for contact stress distribution calculations. However, Hertz Sliding wear is one of the most common contact model has assumptions, such as all wear types that takes place in different bodies are considered elastic, the contact mechanical contacts. It has been suggested between them is ellipse-shaped, frictionless that the dominant parameters that influence and non-conforming. the sliding wear rate are loading and For sphere on plane surface contact (see sliding parameters of contact [1,2]. The Fig.1) the contact radius r (m) can be given sliding law of contact is easily determined as: by mechanism kinematics. The calculation of contact stress in the sliding contact area, 3F R r = 3 N 1 , (3) defined by loading and the shapes of 4E* contact bodies, is more complicated process. According to the linear wear where R1 is the radius of sphere (m) and models, the volume wear directly depends E* is the normalized elasticity modulus on normal pressure in the contact. (Pa) defined by equation: 71 1 FEM program ANSYS Workbench 14.5 E* = , (4) 2 2 was used for Hertz contact model (1− µ1 ) (1− µ2 ) + calculations. The axisymmetric 2-D model E1 E2 was created to save the calculation time. The isotropic sphere had an axial modulus where E1, E2 and μ1, μ2 are the moduli of elasticity (Pa) and Poisson’s ratios of of elasticity (E1) of 200 GPa (steel) and a two contact bodies’ materials. Poisson’s ratio (μ1) of 0.3. The sphere was pressed vertically to the contact interface FN with a rigid counterbody – rigid plane R1 (plane surface). The modulus of elasticity of rigid plane (E2) was assumed to be +∞ and Poisson’s ratio (μ2) equals 0. After model geometry designed the mesh was configured (see Fig 2). The edge Fig.1. Sphere on plane surface contact. sizing function was used in the contact area to refine the mesh. The greater is the The normal contact pressure p distribution number of elements near contact the better is dependent on the contact radius r with the results will converge within appropriate -6 the maximum value pmax (Pa) in the center bounds. Contact element size of 5∙10 m of the contact area: was selected and number of elements was equal to 20787. This contact element size 3FN gives the most optimum normal contact pmax = 2 (5) 2πr pressure results accuracy along with acceptable duration of numerical The numerical method - finite element simulation and analysis. method (FEM) can be used as an alternative method for contact pressure determination. This method is useful for complex systems, when analytical solutions are not available. FEM is based on considering the bodies as sets of discrete elements and on finding approximate solutions to boundary value problems what is solutions to differential equations that satisfy these boundary conditions, of the elements. The use of Fig. 2. Mesh of the Hertz contact model. FEM together with appropriate wear To prevent the two surfaces from passing models is probably the only possible through each other, Augmented Lagrange method to be used for coated system wear contact formulation method was used. characteristics calculation. According to Augmented Lagrange method the higher is contact stiffness the lower is 2. FEM application for sphere-on-plane penetration [5]: contact model 2.1 Hertz contact model of uncoated FN = k N x p + λ , (6) contact where kN is contact normal stiffness Before making FEM simulations with (N/m), xp is surface penetration (m), λ is complicated coated system, Hertz contact an extra term (N) that makes this method model with the simple uncoated bodies less sensitive to the magnitude of the must be used in order to verify the FEM contact stiffness in comparison to model. Pure Penalty method [5]. For general bulk 72 deformation–dominated problems it is FKN FKN FKN recommended by ANSYS [5] to use the =1 =10 =100 Numerical normal contact normal contact stiffness factor (FKN). 899 1002 1020 FKN specifies a scaling factor for contact pressure pmax, (MPa) stiffness that is automatically calculated by Table 3. Numerical results of maximum ANSYS. The scaling factors are usually in normal contact pressure pmax, (MPa) for the range of FKN = (1...100) between different FKN values. sphere edge and rigid plane surface. The higher is the value of contact normal Figure 3 demonstrates the FEM stiffness, the more accurate is the result of distribution of normal contact pressure in FEM simulation. However, too high FKN the contact area if FKN = 10. values cause difficulties with convergence. Frictionless contact was selected for Hertz contact model as frictionless behaviour allows the bodies to slide relative to one another without any resistance [5]. Sphere was defined to be the contact body. Plane was defined as rigid target body. Finally the asymmetric behaviour of contact was specified. The asymmetric behaviour of contact means that only the contact surfaces are constrained from penetrating the target surfaces. The normal force of Fig. 3. Normal contact pressure distribution in Hertz contact (FKN = 10). FN = 1 N and sphere radius R1 = 0.003 m were used in FEM simulation. In tables 1 Result of the numerical simulation of and 2 the results of analytical and uncoated Hertz contact revealed that numerical contact radius and maximum optimal number of elements, element size normal contact pressure are presented. and contact normal stiffness values are Relative critical for normal contact pressure Analytical Numerical error (%) numerical calculations. Contact radius 0.0217 0.022 4.4 r, (mm) 2.2 Sphere–on–plane contact model for Table 1. Analytical and numerical results coated contact of contact radius r, (mm), FKN = 10. Hertz elastic contact theory formulae can Relative Analytical Numerical be applied only in case of uncoated error (%) systems. Experimental research is therefore Normal contact 987 (acc. to mostly used for coated systems wear pressure pmax, 1013 r value) 2.6 (MPa) 1002 characteristics analysis. Using FEM Table 2. Analytical and numerical results numerical method for coated bodies wear of maximum normal contact pressure pmax, simulation is therefore highly interesting. (MPa), FKN = 10. Although sliding wear is affected by many aspects, such as substrate and coating According to the ANSYS solution results, materials physical and chemical properties, the relative error of the normal contact sliding velocity, wear test duration, pressure numerical calculation is 2.6 %. temperature and humidity etc., the normal The optimal value of FKN = 10 was contact pressure associated with normal selected previously from a number of Hertz loading and contact bodies shapes is one of contact simulation results with different the most important parameters that should FKN values (see Table 3). be determined. The use of FEM numerical 73 simulations for coated systems contact properly explored. However some pressure prognosis helps to define the most researchers [9,10,11] have found that wear suitable coatings for different substrate resistance increases with modulus of materials. elasticity increase. Materials with a higher In this work coated sphere on rigid modulus of elasticity usually have higher uncoated plane contact model was done hardness. 6 with the coated sphere radius R1 = 0.003 m Previous experimental research [ ] revealed and the normal force FN = 1 N as before. that coatings with lower modulus of elasticity and E/H ratio like AlTiN have Substrate Hardness Modulus of lower dimensional coefficient of wear Substrate material H elasticity 3 type 1 (CoW) k (mm /Nm) on substrates with designation (HV) E (GPa) 1 higher modulus of elasticity (HM) (see SF CWTS Weartec™ 843 HV0.01 199 Table 6). PM CWTS Vanadis 6 843 HV0.01 210 NS 38CrMoAl8 850 HV0.01 300 TiCN/ TiCN/ AlTiN/ AlTiN/ H15 CWTS HM CWTS HM HM 1555 HV0.3 590 (WC-15Co) 1. CoW k -5 -5 3 2,2·10 - 7,6·10 Table 4. Mechanical properties of substrate (mm /Nm); - 2. CoW k materials. - 1·10-5 - 6,9·10-5 (mm3/Nm); Mechanical properties of investigated Table 6.
Load more

Recommended publications
  • Wear – Materials, Mechanisms and Practice
    WEAR – MATERIALS, MECHANISMS AND PRACTICE Edited by Gwidon W. Stachowiak WEAR – MATERIALS, MECHANISMS AND PRACTICE Editors: M.J. Neale, T.A. Polak and M. Priest Guide to Wear Problems and Testing for Industry M.J. Neale and M. Gee Handbook of Surface Treatment and Coatings M. Neale, T.A. Polak, and M. Priest (Eds) Lubrication and Lubricant Selection – A Practical Guide, 3rd Edition A.R. Lansdown Rolling Contacts T.A. Stolarski and S. Tobe Total Tribology – Towards an integrated approach I. Sherrington, B. Rowe and R. Wood (Eds) Tribology – Lubrication, Friction and Wear I.V. Kragelsky, V.V. Alisin, N.K. Myshkin and M.I. Petrokovets Wear – Materials, Mechanisms and Practice G. Stachowiak (Ed.) WEAR – MATERIALS, MECHANISMS AND PRACTICE Edited by Gwidon W. Stachowiak Copyright © 2005 John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England Telephone (+44) 1243 779777 Chapter 1 Copyright © I.M. Hutchings Email (for orders and customer service enquiries): [email protected] Visit our Home Page on www.wiley.com Reprinted with corrections May 2006 All Rights Reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except under the terms of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London W1T 4LP, UK, without the permission in writing of the Publisher. Requests to the Publisher should be addressed to the Permissions Department, John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England, or emailed to [email protected], or faxed to (+44) 1243 770620.
    [Show full text]
  • UNIT-2: “WEAR &Types of WEAR”
    UNIT-2: “WEAR &TYPEs of WEAR” Lecture by Dr. Mukund Dutt Sharma, Assistant Professor Department of Mechanical Engineering National Institute of Technology Srinagar – 190 006 (J & K) India E-mail: [email protected] Website: http://nitsri.ac.in/ Instructional Objectives After studying this unit, you should be able to understand: • Classification of Wear, • Theories of adhesive, abrasive, surface fatigue and corrosives wear, erosive, cavitation and fretting wear. NATIONAL INSTITUTE OF TECHNOLOGY, SRINAGAR, J&K, INDIA 11 April 2020 2 Wear INTRODUCTION Wear is defined as the undesirable but inevitable removal of material from the rubbing surfaces. Though the removal of material from the surface is small, it leads to a reduction in operating efficiency. The more frequent replacement or repair of worn components and overhauling of the machinery may cost enormously in terms of labour, machine down-time and energy in the manufacture of spares. The term wear is used to describe the progressive deterioration of the surface with loss of shape often accompanied by loss of weight and the creation of debris. Through, at the outset wear appears to be simple, the actual process of removal of material is very complex. This is because of a large number of factors which influence wear. NATIONAL INSTITUTE OF TECHNOLOGY, SRINAGAR, J&K, INDIA 11 April 2020 3 Wear (Cont..) INTRODUCTION The major factors influencing wear are given below: Variable connected with metallurgy. Hardness. Toughness. Constitution and structure. Chemical composition. Variables connected with service. Contacting materials. Pressure. Speed. Temperature. Other contributing factors. Lubrication. NATIONAL INSTITUTE OF Corrosion. TECHNOLOGY, SRINAGAR, J&K, INDIA 11 April 2020 4 Wear (Cont..) INTRODUCTION Wear is a process of gradual removal of a material from surfaces of solids subject to contact and sliding.
    [Show full text]
  • 3Rd Edition A.R
    WEAR – MATERIALS, MECHANISMS AND PRACTICE Editors: M.J. Neale, T.A. Polak and M. Priest Guide to Wear Problems and Testing for Industry M.J. Neale and M. Gee Handbook of Surface Treatment and Coatings M. Neale, T.A. Polak, and M. Priest (Eds) Lubrication and Lubricant Selection – A Practical Guide, 3rd Edition A.R. Lansdown Rolling Contacts T.A. Stolarski and S. Tobe Total Tribology – Towards an integrated approach I. Sherrington, B. Rowe and R. Wood (Eds) Tribology – Lubrication, Friction and Wear I.V. Kragelsky, V.V. Alisin, N.K. Myshkin and M.I. Petrokovets Wear – Materials, Mechanisms and Practice G. Stachowiak (Ed.) WEAR – MATERIALS, MECHANISMS AND PRACTICE Edited by Gwidon W. Stachowiak Copyright © 2005 John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England Telephone (+44) 1243 779777 Chapter 1 Copyright © I.M. Hutchings Email (for orders and customer service enquiries): [email protected] Visit our Home Page on www.wiley.com Reprinted with corrections May 2006 All Rights Reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except under the terms of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London W1T 4LP, UK, without the permission in writing of the Publisher. Requests to the Publisher should be addressed to the Permissions Department, John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England, or emailed to [email protected], or faxed to (+44) 1243 770620.
    [Show full text]
  • Experimental Study and Verification of Wear for Glassreinforced Polymer
    Global Journal of Researches in Engineering: A Mechanical and Mechanics Engineering Volume 14 Issue 3 Version 1.0 Year 2014 Type: Double Blind Peer Reviewed International Research Journal Publisher: Global Journals Inc. (USA) Online ISSN: 2249-4596 & Print ISSN: 0975-5861 Experimental Study and Verification of Wear for Glass Reinforced Polymer using ANSYS By P. Prabhu, M. Suresh Kumar, Ajit Pal Singh & K. Siva Defence University, Ethiopia Abstract- The current design/manufacturing field looking for value added/engineering projects. In this study, an attempt has been aimed to predict the wear of the sliding surfaces in the development stage it self which will be results in the increase of durability of the components. The wear for a polymer-polymer sliding surface contact in dry condition can be obtained by creating simulation. There are two inputs required for determining the wear volume loss over its usage time. One is the nodal pressure value at the contact area for small sliding steps which can be calculated by subjecting the geometrical model to the finite element analysis. ANSYS was used as finite element tool. Another one is the friction coefficient which can be obtained by custom designed experiments. For the calculation of friction coefficient, prototype to be subjected to unlubricated pin-on-disc experimental setup. The wear rate can be calculated by graph by plotting between pressure and cycles. Swiveling of mirror over the base resulted in the wear. By the above techniques, the wear loss and reliability of the rear mirror can be predicted. Keywords: glass reinforced polymer, wear, sliding contact, CATIA and ANSYS.
    [Show full text]
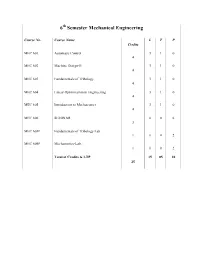
  • 6 Semester Mechanical Engineering
    6th Semester Mechanical Engineering Course No. Course Name L T P Credits MEC 601 Automatic Control 3 1 0 4 MEC 602 Machine Design-II 3 1 0 4 MEC 603 Fundamentals of Tribology 3 1 0 4 MEC 604 Linear Optimization in Engineering 3 1 0 4 MEC 605 Introduction to Mechatronics 3 1 0 4 MEC 606 SEMINAR 0 0 6 3 MEC 603P Fundamentals of Tribology Lab. 1 0 0 2 MEC 605P Mechatronics-Lab. 1 0 0 2 Total of Credits & LTP 15 05 10 25 Course No.: MEC 601 AUTOM\TIC CONTROL C L T(4 3 1) COURSE OUTCOME: 1. Develop the mathematical models of LTI dynamic systems,determine their transfer functions,describe quantitatively the transient response of LTI systems,interpret and apply block diagram representations of control systems and understand the consequences of feedback. 2. Use poles and zeroes of the transfer functions to determine the time response and performance characteristics and design PID controllers using empirical tuning rules. 3. Determine the stability of linear control systems using the Routh-Hurwitzcriterion and classify systems as asymptotically and BIBO stable or unstable. 4. Determine the effect of loop gain variations on the locationof closed-loop scales,sketch the root locus and use it to evaluate parameter values to meet the transient reponse specification od closed loop systems. 5. Define the frequency response and plot asymptotic approximations to the frequency response fumction of a system.Sketch a Nyquist diagram and use the Nyquist criterion to determine the stability of a system. UNIT I Introduction: Concept of automatic control, open loop and closed loop systems, servo mechanism, block diagram, transfer function.
    [Show full text]
  • A Mechanistic Understanding of the Wear Coefficient: from Single To
    A mechanistic understanding of the wear coefficient: From single to multiple asperities contact Lucas Frérota,∗, Ramin Aghababaeia,b, Jean-François Molinaria aInstitute of Civil Engineering, École Polytechnique Fédérale de Lausanne (EPFL), CH 1015 Lausanne, Switzerland bDepartment of Engineering — Mechanical Engineering, Aarhus University, 8000 Aarhus, Denmark Abstract Sliding contact between solids leads to material detaching from their surfaces in the form of debris particles, a process known as wear. According to the well-known Archard wear model, the wear volume (i.e. the volume of detached particles) is proportional to the load and the sliding distance, while being inversely proportional to the hardness. The influence of other parameters are empirically merged into a factor, referred to as wear coefficient, which does not stem from any theoretical development, thus limiting the predictive capacity of the model. Based on a recent understanding of a critical length-scale controlling wear particle formation, we present two novel derivations of the wear coefficient: one based on Archard’s interpretation of the wear coefficient as the probability of wear particle detachment and one that follows naturally from the up-scaling of asperity-level physics into a generic multi-asperity wear model. As a result, the variation of wear rate and wear coefficient are discussed in terms of the properties of the interface, surface roughness parameters and applied load for various rough contact situations. Both new wear interpretations are evaluated analytically and numerically, and recover some key features of wear observed in experiments. This work shines new light on the understanding of wear, potentially opening a pathway for calculating the wear coefficient from first principles.
    [Show full text]
  • Experimental Analysis and Modeling for Reciprocating Wear Behavior of Nanocomposite Coatings
    Experimental Analysis and Modeling for Reciprocating Wear Behavior of Nanocomposite Coatings Mian Hammad Nazir1, Zulfiqar Ahmad Khan1*, Adil Saeed1, Vasilios Bakolas2, Wolfgang Braun2, Rizwan Bajwa1 1NanoCorr Energy and Modelling Research Group (NCEM), Bournemouth University Talbot Campus, Poole, Dorset, BH12 5BB, UK *Email: [email protected] 2Advanced Bearing Analysis Schaeffler Technologies AG & Co. KG, 91074 Herzogenaurach, Germany Abstract This paper presents the study of wear responses of nanocomposite coatings with a steel ball under oscillating- reciprocating state. Nanocomposite coatings for this study include: Nickel-Alumina (Ni/Al2O3), Nickel-Silicon Carbide (Ni/SiC), Nickel-Zirconia (Ni/ZrO2) and Ni/Graphene. Ni/ZrO2 exhibited maximum wear rate followed by Ni/SiC, Ni/Al2O3 and Ni/Graphene respectively which was also assured by Scanning Electron Microscopy (SEM) micrographs, grain sizes, hardness, porosity, surface stresses, frictional coefficients behaviours and “U- shaped” wear depth profiles. The “U-shaped” profiles were utilised to calculate the energy distribution (Archard factor density) along the interface. A novel mechano-wear model incorporating the energy distribution equations with the mechanics equations was developed for analysing the effects of intrinsic mechanical properties (such as grain sizes, hardness, porosity, surface stresses of the nanocomposite coatings) on the wear response. The predictions showed close agreement with the experimental results. In conclusion Ni/Graphene exhibited better anti-wear properties compared to other nanocomposite coatings. The high anti-wear behaviour of Ni/Graphene composite is due to enhanced strengthening effects in the presence of graphene. The importance of this work is evident from various industrial applications which require reliable modelling techniques to predict coatings failures due to wear.
    [Show full text]
  • Ultralow Nanoscale Wear Through Atom-By-Atom Attrition in Silicon-Containing Diamond-Like Carbon
    LETTERS PUBLISHED ONLINE: 31 JANUARY 2010 | DOI: 10.1038/NNANO.2010.3 Ultralow nanoscale wear through atom-by-atom attrition in silicon-containing diamond-like carbon Harish Bhaskaran1*†, Bernd Gotsmann1, Abu Sebastian1, Ute Drechsler1, Mark A. Lantz1, Michel Despont1*, Papot Jaroenapibal2†,RobertW.Carpick2,YunChen3† and Kumar Sridharan3 Understanding friction1–4 and wear5–11 at the nanoscale is The wear performance of these nanoscale tips was then evaluated important for many applications that involve nanoscale com- for sliding wear on SiO2 in an atomic force microscope (AFM). The ponents sliding on a surface, such as nanolithography, nano- effects of substrate wear were minimized by carefully choosing the metrology and nanomanufacturing. Defects, cracks and other scan pattern (see Supplementary Information). Wear was measured phenomena that influence material strength and wear at macro- in situ as an increase in adhesion corresponding to an increase in the scopic scales are less important at the nanoscale, which is why contact area between the tip and substrate. This was correlated to a nanowires can, for example, show higher strengths than bulk change in tip radius using the parameter uadh (see Methods). At the samples12. The contact area between the materials must also be macroscale, wear is a result of a combination of processes including described differently at the nanoscale13. Diamond-like carbon is fracture, plasticity and third-body effects, as well as atom-by-atom routinely used as a surface coating in applications that require attrition, and has traditionally been described using Archard’s phe- low friction and wear because it is resistant to wear at the nomenological model21.
    [Show full text]
  • Engineering Design for Wear Second Edition, Revised and Expanded
    Engineering Design for Wear Second Edition, Revised and Expanded Raymond G. Bayer Tribology Consultant Vestal, New York, U.S.A. MARCEL DEKKER, INC. NEW YORK · BASEL Copyright © 2004 Marcel Dekker, Inc. This edition is expanded and updated from a portion of the first edition, Mechanical Wear Prediction and Prevention (Marcel Dekker, 1994). The remaining material in the first edition has been expanded and updated for Mechanical Wear Fundamentals and Testing: Second Edition, Revised and Expanded (Marcel Dekker, 2004). Although great care has been taken to provide accurate and current information, neither the author(s) nor the publisher, nor anyone else associated with this publication, shall be liable for any loss, damage, or liability directly or indirectly caused or alleged to be caused by this book. The material contained herein is not intended to provide specific advice or recommendations for any specific situation. Trademark notice: Product or corporate names may be trademarks or registered trademarks and are used only for identification and explanation without intent to infringe. Library of Congress Cataloging-in-Publication Data A catalog record for this book is available from the Library of Congress. ISBN: 0-8247-4772-0 This book is printed on acid-free paper. Headquarters Marcel Dekker, Inc., 270 Madison Avenue, New York, NY 10016, U.S.A. tel: 212-696-9000; fax: 212-685-4540 Distribution and Customer Service Marcel Dekker, Inc., Cimarron Road, Monticello, New York 12701, U.S.A. tel: 800-228-1160; fax: 845-796-1772 Eastern Hemisphere Distribution Marcel Dekker AG, Hutgasse 4, Postfach 812, CH-4001 Basel, Switzerland tel: 41-61-260-6300; fax: 41-61-260-6333 World Wide Web http://www.dekker.com The publisher offers discounts on this book when ordered in bulk quantities.
    [Show full text]
  • Size Dependence of Nanoscale Wear of Silicon Carbide † † ‡ § † Chaiyapat Tangpatjaroen, David Grierson, Steve Shannon, Joseph E
    Research Article www.acsami.org Size Dependence of Nanoscale Wear of Silicon Carbide † † ‡ § † Chaiyapat Tangpatjaroen, David Grierson, Steve Shannon, Joseph E. Jakes, and Izabela Szlufarska*, † Department of Materials Science & Engineering, University of WisconsinMadison, Madison, Wisconsin 53706, United States ‡ Department of Nuclear Engineering, North Carolina State University, Raleigh, North Carolina 27695, United States § Forest Biopolymers Science and Engineering, USDA Forest Service, Forest Products Laboratory, One Gifford Pinchot Drive, Madison, Wisconsin 53726, United States *S Supporting Information ABSTRACT: Nanoscale, single-asperity wear of single-crystal silicon carbide (sc- SiC) and nanocrystalline silicon carbide (nc-SiC) is investigated using single-crystal diamond nanoindenter tips and nanocrystalline diamond atomic force microscopy (AFM) tips under dry conditions, and the wear behavior is compared to that of single-crystal silicon with both thin and thick native oxide layers. We discovered a transition in the relative wear resistance of the SiC samples compared to that of Si as a function of contact size. With larger nanoindenter tips (tip radius ≈ 370 nm), the wear resistances of both sc-SiC and nc-SiC are higher than that of Si. This result is expected from the Archard’s equation because SiC is harder than Si. However, with the smaller AFM tips (tip radius ≈ 20 nm), the wear resistances of sc-SiC and nc- SiC are lower than that of Si, despite the fact that the contact pressures are comparable to those applied with the nanoindenter tips, and the plastic zones are well-developed in both sets of wear experiments. We attribute the decrease in the relative wear resistance of SiC compared to that of Si to a transition from a wear regime dominated by the materials’ resistance to plastic deformation (i.e., hardness) to a regime dominated by the materials’ resistance to interfacial shear.
    [Show full text]
  • A Combined Wear-Fatigue Design Methodology for Fretting in The
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Repository@Nottingham A combined wear-fatigue design methodology for fretting in the pressure armour layer of flexible marine risers S.M. O’Hallorana, P.H. Shipwayb, A.D. Connairec, S.B. Leena1*, A.M. Harted1 a Mechanical Engineering, National University of Ireland, Galway, Ireland b Faculty of Engineering, University of Nottingham, Nottingham, UK c Wood Group Kenny, Galway Technology Park, Parkmore, Galway, Ireland d Civil Engineering, National University of Ireland, Galway, Ireland 1 Joint senior authors * Corresponding author: Prof. Sean Leen, [email protected] Abstract This paper presents a combined experimental and computational methodology for fretting wear-fatigue prediction of pressure armour wire in flexible marine risers. Fretting wear, friction and fatigue parameters of pressure armour material have been characterised experimentally. A combined fretting wear-fatigue finite element model has been developed using an adaptive meshing technique and the effect of bending-induced tangential slip has been characterised. It has been shown that a surface damage parameter combined with a multiaxial fatigue parameter can accurately predict the beneficial effect of fretting wear on fatigue predictions. This provides a computationally efficient design tool for fretting in the pressure armour layer of flexible marine risers. Keywords: Fretting wear, fretting crack initiation, fretting life prediction, flexible risers, pressure armour wire 1 1 Introduction Fretting is a form of surface damage that occurs between nominally static surfaces in contact experiencing cyclic tangential loading, resulting in a non-uniform, small-scale (typically micro- or nano-scale) relative slip.
    [Show full text]
  • Adhesive Wear Mechanisms Uncovered by Atomistic Simulations
    Friction 6(3): 245–259 (2018) ISSN 2223-7690 https://doi.org/10.1007/s40544-018-0234-6 CN 10-1237/TH REVIEW ARTICLE Adhesive wear mechanisms uncovered by atomistic simulations Jean-François MOLINARI1,*, Ramin AGHABABAEI2, Tobias BRINK1, Lucas FRÉROT1, Enrico MILANESE1 1 Civil Engineering Department, Materials Science Department, École Polytechnique Fédérale de Lausanne, Lausanne 1015, Switzerland 2 Department of Engineering - Mechanical Engineering, Aarhus Universitet, Aarhus 8000, Denmark Received: 01 May 2018 / Revised: 14 July 2018 / Accepted: 16 July 2018 © The author(s) 2018. This article is published with open access at Springerlink.com Abstract: In this review, we discuss our recent advances in modeling adhesive wear mechanisms using coarse-grained atomistic simulations. In particular, we present how a model pair potential reveals the transition from ductile shearing of an asperity to the formation of a debris particle. This transition occurs at a critical junction size, which determines the particle size at its birth. Atomistic simulations also reveal that for nearby asperities, crack shielding mechanisms result in a wear volume proportional to an effective area larger than the real contact area. As the density of microcontacts increases with load, we propose this crack shielding mechanism as a key to understand the transition from mild to severe wear. We conclude with open questions and a road map to incorporate these findings in mesoscale continuum models. Because these mesoscale models allow an accurate statistical representation of rough surfaces, they provide a simple means to interpret classical phenomenological wear models and wear coefficients from physics-based principles. Keywords: adhesive wear; molecular dynamics; continuum mechanics 1 Introduction slow pace of translation of microscopic observations into macroscopic models of the wearing processes and the paucity In 1995, when Meng and Ludema [1] reviewed an of good experiments to verify proposed models”.
    [Show full text]