A Mechanistic Understanding of the Wear Coefficient: from Single To
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Wear – Materials, Mechanisms and Practice
WEAR – MATERIALS, MECHANISMS AND PRACTICE Edited by Gwidon W. Stachowiak WEAR – MATERIALS, MECHANISMS AND PRACTICE Editors: M.J. Neale, T.A. Polak and M. Priest Guide to Wear Problems and Testing for Industry M.J. Neale and M. Gee Handbook of Surface Treatment and Coatings M. Neale, T.A. Polak, and M. Priest (Eds) Lubrication and Lubricant Selection – A Practical Guide, 3rd Edition A.R. Lansdown Rolling Contacts T.A. Stolarski and S. Tobe Total Tribology – Towards an integrated approach I. Sherrington, B. Rowe and R. Wood (Eds) Tribology – Lubrication, Friction and Wear I.V. Kragelsky, V.V. Alisin, N.K. Myshkin and M.I. Petrokovets Wear – Materials, Mechanisms and Practice G. Stachowiak (Ed.) WEAR – MATERIALS, MECHANISMS AND PRACTICE Edited by Gwidon W. Stachowiak Copyright © 2005 John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England Telephone (+44) 1243 779777 Chapter 1 Copyright © I.M. Hutchings Email (for orders and customer service enquiries): [email protected] Visit our Home Page on www.wiley.com Reprinted with corrections May 2006 All Rights Reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except under the terms of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London W1T 4LP, UK, without the permission in writing of the Publisher. Requests to the Publisher should be addressed to the Permissions Department, John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England, or emailed to [email protected], or faxed to (+44) 1243 770620. -

UNIT-2: “WEAR &Types of WEAR”
UNIT-2: “WEAR &TYPEs of WEAR” Lecture by Dr. Mukund Dutt Sharma, Assistant Professor Department of Mechanical Engineering National Institute of Technology Srinagar – 190 006 (J & K) India E-mail: [email protected] Website: http://nitsri.ac.in/ Instructional Objectives After studying this unit, you should be able to understand: • Classification of Wear, • Theories of adhesive, abrasive, surface fatigue and corrosives wear, erosive, cavitation and fretting wear. NATIONAL INSTITUTE OF TECHNOLOGY, SRINAGAR, J&K, INDIA 11 April 2020 2 Wear INTRODUCTION Wear is defined as the undesirable but inevitable removal of material from the rubbing surfaces. Though the removal of material from the surface is small, it leads to a reduction in operating efficiency. The more frequent replacement or repair of worn components and overhauling of the machinery may cost enormously in terms of labour, machine down-time and energy in the manufacture of spares. The term wear is used to describe the progressive deterioration of the surface with loss of shape often accompanied by loss of weight and the creation of debris. Through, at the outset wear appears to be simple, the actual process of removal of material is very complex. This is because of a large number of factors which influence wear. NATIONAL INSTITUTE OF TECHNOLOGY, SRINAGAR, J&K, INDIA 11 April 2020 3 Wear (Cont..) INTRODUCTION The major factors influencing wear are given below: Variable connected with metallurgy. Hardness. Toughness. Constitution and structure. Chemical composition. Variables connected with service. Contacting materials. Pressure. Speed. Temperature. Other contributing factors. Lubrication. NATIONAL INSTITUTE OF Corrosion. TECHNOLOGY, SRINAGAR, J&K, INDIA 11 April 2020 4 Wear (Cont..) INTRODUCTION Wear is a process of gradual removal of a material from surfaces of solids subject to contact and sliding. -

3Rd Edition A.R
WEAR – MATERIALS, MECHANISMS AND PRACTICE Editors: M.J. Neale, T.A. Polak and M. Priest Guide to Wear Problems and Testing for Industry M.J. Neale and M. Gee Handbook of Surface Treatment and Coatings M. Neale, T.A. Polak, and M. Priest (Eds) Lubrication and Lubricant Selection – A Practical Guide, 3rd Edition A.R. Lansdown Rolling Contacts T.A. Stolarski and S. Tobe Total Tribology – Towards an integrated approach I. Sherrington, B. Rowe and R. Wood (Eds) Tribology – Lubrication, Friction and Wear I.V. Kragelsky, V.V. Alisin, N.K. Myshkin and M.I. Petrokovets Wear – Materials, Mechanisms and Practice G. Stachowiak (Ed.) WEAR – MATERIALS, MECHANISMS AND PRACTICE Edited by Gwidon W. Stachowiak Copyright © 2005 John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England Telephone (+44) 1243 779777 Chapter 1 Copyright © I.M. Hutchings Email (for orders and customer service enquiries): [email protected] Visit our Home Page on www.wiley.com Reprinted with corrections May 2006 All Rights Reserved. No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except under the terms of the Copyright, Designs and Patents Act 1988 or under the terms of a licence issued by the Copyright Licensing Agency Ltd, 90 Tottenham Court Road, London W1T 4LP, UK, without the permission in writing of the Publisher. Requests to the Publisher should be addressed to the Permissions Department, John Wiley & Sons Ltd, The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ, England, or emailed to [email protected], or faxed to (+44) 1243 770620. -

Experimental Study and Verification of Wear for Glassreinforced Polymer
Global Journal of Researches in Engineering: A Mechanical and Mechanics Engineering Volume 14 Issue 3 Version 1.0 Year 2014 Type: Double Blind Peer Reviewed International Research Journal Publisher: Global Journals Inc. (USA) Online ISSN: 2249-4596 & Print ISSN: 0975-5861 Experimental Study and Verification of Wear for Glass Reinforced Polymer using ANSYS By P. Prabhu, M. Suresh Kumar, Ajit Pal Singh & K. Siva Defence University, Ethiopia Abstract- The current design/manufacturing field looking for value added/engineering projects. In this study, an attempt has been aimed to predict the wear of the sliding surfaces in the development stage it self which will be results in the increase of durability of the components. The wear for a polymer-polymer sliding surface contact in dry condition can be obtained by creating simulation. There are two inputs required for determining the wear volume loss over its usage time. One is the nodal pressure value at the contact area for small sliding steps which can be calculated by subjecting the geometrical model to the finite element analysis. ANSYS was used as finite element tool. Another one is the friction coefficient which can be obtained by custom designed experiments. For the calculation of friction coefficient, prototype to be subjected to unlubricated pin-on-disc experimental setup. The wear rate can be calculated by graph by plotting between pressure and cycles. Swiveling of mirror over the base resulted in the wear. By the above techniques, the wear loss and reliability of the rear mirror can be predicted. Keywords: glass reinforced polymer, wear, sliding contact, CATIA and ANSYS. -
6 Semester Mechanical Engineering
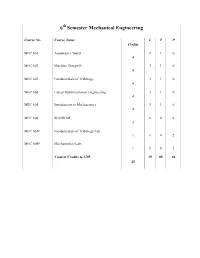
6th Semester Mechanical Engineering Course No. Course Name L T P Credits MEC 601 Automatic Control 3 1 0 4 MEC 602 Machine Design-II 3 1 0 4 MEC 603 Fundamentals of Tribology 3 1 0 4 MEC 604 Linear Optimization in Engineering 3 1 0 4 MEC 605 Introduction to Mechatronics 3 1 0 4 MEC 606 SEMINAR 0 0 6 3 MEC 603P Fundamentals of Tribology Lab. 1 0 0 2 MEC 605P Mechatronics-Lab. 1 0 0 2 Total of Credits & LTP 15 05 10 25 Course No.: MEC 601 AUTOM\TIC CONTROL C L T(4 3 1) COURSE OUTCOME: 1. Develop the mathematical models of LTI dynamic systems,determine their transfer functions,describe quantitatively the transient response of LTI systems,interpret and apply block diagram representations of control systems and understand the consequences of feedback. 2. Use poles and zeroes of the transfer functions to determine the time response and performance characteristics and design PID controllers using empirical tuning rules. 3. Determine the stability of linear control systems using the Routh-Hurwitzcriterion and classify systems as asymptotically and BIBO stable or unstable. 4. Determine the effect of loop gain variations on the locationof closed-loop scales,sketch the root locus and use it to evaluate parameter values to meet the transient reponse specification od closed loop systems. 5. Define the frequency response and plot asymptotic approximations to the frequency response fumction of a system.Sketch a Nyquist diagram and use the Nyquist criterion to determine the stability of a system. UNIT I Introduction: Concept of automatic control, open loop and closed loop systems, servo mechanism, block diagram, transfer function. -

Experimental Analysis and Modeling for Reciprocating Wear Behavior of Nanocomposite Coatings
Experimental Analysis and Modeling for Reciprocating Wear Behavior of Nanocomposite Coatings Mian Hammad Nazir1, Zulfiqar Ahmad Khan1*, Adil Saeed1, Vasilios Bakolas2, Wolfgang Braun2, Rizwan Bajwa1 1NanoCorr Energy and Modelling Research Group (NCEM), Bournemouth University Talbot Campus, Poole, Dorset, BH12 5BB, UK *Email: [email protected] 2Advanced Bearing Analysis Schaeffler Technologies AG & Co. KG, 91074 Herzogenaurach, Germany Abstract This paper presents the study of wear responses of nanocomposite coatings with a steel ball under oscillating- reciprocating state. Nanocomposite coatings for this study include: Nickel-Alumina (Ni/Al2O3), Nickel-Silicon Carbide (Ni/SiC), Nickel-Zirconia (Ni/ZrO2) and Ni/Graphene. Ni/ZrO2 exhibited maximum wear rate followed by Ni/SiC, Ni/Al2O3 and Ni/Graphene respectively which was also assured by Scanning Electron Microscopy (SEM) micrographs, grain sizes, hardness, porosity, surface stresses, frictional coefficients behaviours and “U- shaped” wear depth profiles. The “U-shaped” profiles were utilised to calculate the energy distribution (Archard factor density) along the interface. A novel mechano-wear model incorporating the energy distribution equations with the mechanics equations was developed for analysing the effects of intrinsic mechanical properties (such as grain sizes, hardness, porosity, surface stresses of the nanocomposite coatings) on the wear response. The predictions showed close agreement with the experimental results. In conclusion Ni/Graphene exhibited better anti-wear properties compared to other nanocomposite coatings. The high anti-wear behaviour of Ni/Graphene composite is due to enhanced strengthening effects in the presence of graphene. The importance of this work is evident from various industrial applications which require reliable modelling techniques to predict coatings failures due to wear. -

Ultralow Nanoscale Wear Through Atom-By-Atom Attrition in Silicon-Containing Diamond-Like Carbon
LETTERS PUBLISHED ONLINE: 31 JANUARY 2010 | DOI: 10.1038/NNANO.2010.3 Ultralow nanoscale wear through atom-by-atom attrition in silicon-containing diamond-like carbon Harish Bhaskaran1*†, Bernd Gotsmann1, Abu Sebastian1, Ute Drechsler1, Mark A. Lantz1, Michel Despont1*, Papot Jaroenapibal2†,RobertW.Carpick2,YunChen3† and Kumar Sridharan3 Understanding friction1–4 and wear5–11 at the nanoscale is The wear performance of these nanoscale tips was then evaluated important for many applications that involve nanoscale com- for sliding wear on SiO2 in an atomic force microscope (AFM). The ponents sliding on a surface, such as nanolithography, nano- effects of substrate wear were minimized by carefully choosing the metrology and nanomanufacturing. Defects, cracks and other scan pattern (see Supplementary Information). Wear was measured phenomena that influence material strength and wear at macro- in situ as an increase in adhesion corresponding to an increase in the scopic scales are less important at the nanoscale, which is why contact area between the tip and substrate. This was correlated to a nanowires can, for example, show higher strengths than bulk change in tip radius using the parameter uadh (see Methods). At the samples12. The contact area between the materials must also be macroscale, wear is a result of a combination of processes including described differently at the nanoscale13. Diamond-like carbon is fracture, plasticity and third-body effects, as well as atom-by-atom routinely used as a surface coating in applications that require attrition, and has traditionally been described using Archard’s phe- low friction and wear because it is resistant to wear at the nomenological model21. -

Engineering Design for Wear Second Edition, Revised and Expanded
Engineering Design for Wear Second Edition, Revised and Expanded Raymond G. Bayer Tribology Consultant Vestal, New York, U.S.A. MARCEL DEKKER, INC. NEW YORK · BASEL Copyright © 2004 Marcel Dekker, Inc. This edition is expanded and updated from a portion of the first edition, Mechanical Wear Prediction and Prevention (Marcel Dekker, 1994). The remaining material in the first edition has been expanded and updated for Mechanical Wear Fundamentals and Testing: Second Edition, Revised and Expanded (Marcel Dekker, 2004). Although great care has been taken to provide accurate and current information, neither the author(s) nor the publisher, nor anyone else associated with this publication, shall be liable for any loss, damage, or liability directly or indirectly caused or alleged to be caused by this book. The material contained herein is not intended to provide specific advice or recommendations for any specific situation. Trademark notice: Product or corporate names may be trademarks or registered trademarks and are used only for identification and explanation without intent to infringe. Library of Congress Cataloging-in-Publication Data A catalog record for this book is available from the Library of Congress. ISBN: 0-8247-4772-0 This book is printed on acid-free paper. Headquarters Marcel Dekker, Inc., 270 Madison Avenue, New York, NY 10016, U.S.A. tel: 212-696-9000; fax: 212-685-4540 Distribution and Customer Service Marcel Dekker, Inc., Cimarron Road, Monticello, New York 12701, U.S.A. tel: 800-228-1160; fax: 845-796-1772 Eastern Hemisphere Distribution Marcel Dekker AG, Hutgasse 4, Postfach 812, CH-4001 Basel, Switzerland tel: 41-61-260-6300; fax: 41-61-260-6333 World Wide Web http://www.dekker.com The publisher offers discounts on this book when ordered in bulk quantities. -

Size Dependence of Nanoscale Wear of Silicon Carbide † † ‡ § † Chaiyapat Tangpatjaroen, David Grierson, Steve Shannon, Joseph E
Research Article www.acsami.org Size Dependence of Nanoscale Wear of Silicon Carbide † † ‡ § † Chaiyapat Tangpatjaroen, David Grierson, Steve Shannon, Joseph E. Jakes, and Izabela Szlufarska*, † Department of Materials Science & Engineering, University of WisconsinMadison, Madison, Wisconsin 53706, United States ‡ Department of Nuclear Engineering, North Carolina State University, Raleigh, North Carolina 27695, United States § Forest Biopolymers Science and Engineering, USDA Forest Service, Forest Products Laboratory, One Gifford Pinchot Drive, Madison, Wisconsin 53726, United States *S Supporting Information ABSTRACT: Nanoscale, single-asperity wear of single-crystal silicon carbide (sc- SiC) and nanocrystalline silicon carbide (nc-SiC) is investigated using single-crystal diamond nanoindenter tips and nanocrystalline diamond atomic force microscopy (AFM) tips under dry conditions, and the wear behavior is compared to that of single-crystal silicon with both thin and thick native oxide layers. We discovered a transition in the relative wear resistance of the SiC samples compared to that of Si as a function of contact size. With larger nanoindenter tips (tip radius ≈ 370 nm), the wear resistances of both sc-SiC and nc-SiC are higher than that of Si. This result is expected from the Archard’s equation because SiC is harder than Si. However, with the smaller AFM tips (tip radius ≈ 20 nm), the wear resistances of sc-SiC and nc- SiC are lower than that of Si, despite the fact that the contact pressures are comparable to those applied with the nanoindenter tips, and the plastic zones are well-developed in both sets of wear experiments. We attribute the decrease in the relative wear resistance of SiC compared to that of Si to a transition from a wear regime dominated by the materials’ resistance to plastic deformation (i.e., hardness) to a regime dominated by the materials’ resistance to interfacial shear. -

A Combined Wear-Fatigue Design Methodology for Fretting in The
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Repository@Nottingham A combined wear-fatigue design methodology for fretting in the pressure armour layer of flexible marine risers S.M. O’Hallorana, P.H. Shipwayb, A.D. Connairec, S.B. Leena1*, A.M. Harted1 a Mechanical Engineering, National University of Ireland, Galway, Ireland b Faculty of Engineering, University of Nottingham, Nottingham, UK c Wood Group Kenny, Galway Technology Park, Parkmore, Galway, Ireland d Civil Engineering, National University of Ireland, Galway, Ireland 1 Joint senior authors * Corresponding author: Prof. Sean Leen, [email protected] Abstract This paper presents a combined experimental and computational methodology for fretting wear-fatigue prediction of pressure armour wire in flexible marine risers. Fretting wear, friction and fatigue parameters of pressure armour material have been characterised experimentally. A combined fretting wear-fatigue finite element model has been developed using an adaptive meshing technique and the effect of bending-induced tangential slip has been characterised. It has been shown that a surface damage parameter combined with a multiaxial fatigue parameter can accurately predict the beneficial effect of fretting wear on fatigue predictions. This provides a computationally efficient design tool for fretting in the pressure armour layer of flexible marine risers. Keywords: Fretting wear, fretting crack initiation, fretting life prediction, flexible risers, pressure armour wire 1 1 Introduction Fretting is a form of surface damage that occurs between nominally static surfaces in contact experiencing cyclic tangential loading, resulting in a non-uniform, small-scale (typically micro- or nano-scale) relative slip. -

Adhesive Wear Mechanisms Uncovered by Atomistic Simulations
Friction 6(3): 245–259 (2018) ISSN 2223-7690 https://doi.org/10.1007/s40544-018-0234-6 CN 10-1237/TH REVIEW ARTICLE Adhesive wear mechanisms uncovered by atomistic simulations Jean-François MOLINARI1,*, Ramin AGHABABAEI2, Tobias BRINK1, Lucas FRÉROT1, Enrico MILANESE1 1 Civil Engineering Department, Materials Science Department, École Polytechnique Fédérale de Lausanne, Lausanne 1015, Switzerland 2 Department of Engineering - Mechanical Engineering, Aarhus Universitet, Aarhus 8000, Denmark Received: 01 May 2018 / Revised: 14 July 2018 / Accepted: 16 July 2018 © The author(s) 2018. This article is published with open access at Springerlink.com Abstract: In this review, we discuss our recent advances in modeling adhesive wear mechanisms using coarse-grained atomistic simulations. In particular, we present how a model pair potential reveals the transition from ductile shearing of an asperity to the formation of a debris particle. This transition occurs at a critical junction size, which determines the particle size at its birth. Atomistic simulations also reveal that for nearby asperities, crack shielding mechanisms result in a wear volume proportional to an effective area larger than the real contact area. As the density of microcontacts increases with load, we propose this crack shielding mechanism as a key to understand the transition from mild to severe wear. We conclude with open questions and a road map to incorporate these findings in mesoscale continuum models. Because these mesoscale models allow an accurate statistical representation of rough surfaces, they provide a simple means to interpret classical phenomenological wear models and wear coefficients from physics-based principles. Keywords: adhesive wear; molecular dynamics; continuum mechanics 1 Introduction slow pace of translation of microscopic observations into macroscopic models of the wearing processes and the paucity In 1995, when Meng and Ludema [1] reviewed an of good experiments to verify proposed models”. -

Analytical and Experimental Studies on Wear Behaviour
Analytical and Experimental Studies on Wear Behaviour of Cast and Heat Treated AlSi12CuMgNi and AlZn6MgCu Matrix Composites Reinforced with Ceramic Particles, Under Sliding Conditions ANALYTICAL AND EXPERIMENTAL STUDIES ON WEAR BEHAVIOUR OF CAST AND HEAT TREATED ALSI12CUMGNI AND ALZN6MGCU MATRIX COMPOSITES REINFORCED WITH CERAMIC PARTICLES, UNDER SLIDING CONDITIONS Ileana NicoletaPopescu1, Ivona Camelia Petre2,* and Veronica Despa3 1,2,3 Valahia University of Targoviste, 13 AleeaSinaia Street, Targoviste, Romania E-mail: [email protected] Abstract: The working conditions of the composite materials used to produce machine parts lead to different forms of wear. The fact that, for example, for a a kinematic coupling with sliding motion is often used a material with higher hardness (cast iron, steel) in combination with a material with a lower hardness (a composite material) there is the possibility of wear through abrasion and local plastic deformations. The paper proposes an analytical model for the determination of wear, depending on the angle of inclination of the roughness of the hard surface. The experimental wear investigations were made on cast iron disc (300HB hardness) at room temperature using a “pin on disc” machine, at and contact pressure and sliding speed. The composite consisted from cast and heat treated AlSi12CuMgNi and AlZn6MgCu matrix reinforced with Al2O3 and Graphite combined in different proportion, in the 0-5 volume percent range. The experimental results of the wear for the different materials are analyzed and compared to the analytical ones. The comparison of the experimental and the theoretical results confirms the veracity of the model and corresponds with many of the experimental results obtained in the specialized works.