Master Thesis Civil Engineering - Transport and Planning G.J
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

GEMEENTEBLAD 19 April
Nr. 82180 19 april GEMEENTEBLAD 2018 Officiële uitgave van de gemeente Amsterdam Wijziging instelling invaarverbod en verplichte vaarrichting Singelgracht, gemeente Amsterdam De algemeen directeur van de Stichting Waternet Overwegende: - dat burgemeester en wethouders met hun besluit van 19 december 2017 (Gemeenteblad 2017, nummer Nr. 224180) de algemeen directeur van de Stichting Waternet hebben aangewezen om namens hen de bevoegdheden uit te oefenen als bedoeld in de Verordening op het binnenwater (VOB) en de Scheepvaartverkeerswet; - dat bij besluit van 1 december 2017 de algemeen directeur onder mandaat heeft verleend aan de programmadirecteur Nautische zaken; - dat in het kader van de besluitvorming rond de Nota Varen in Amsterdam een pilot is gehouden met de verkeersmaatregel eenrichtingsverkeer in een deel van de Singelgracht en van de Prinsen- gracht in de periode van januari-september 2014; - dat uit een evaluatie van deze pilot naar voren is gekomen dat de verkeersmaatregelen tijdens de pilot het gewenste gevolg hebben opgeleverd, namelijk beperking van de overlast op de Sin- gelgracht en de Prinsengracht en dat daarom is besloten tot het voortzetten van het eenrichting- verkeer gedurende elk vaarseizoen tussen 01 april en 01 oktober; - dat tot dit eenrichtingsverkeer voor delen van de Singelgracht en delen van de Prinsengracht besloten is bij besluit van 15 april 2015 (Gemeenteblad 2015, afdeling 3B, nummer 68); - dat per apart besluit met ingang van 01 april 2018 de pilot waarbij voor onder meer de gehele Prinsengracht eenrichtingsverkeer -

BRT in Amsterdam Kaart Achter De Burgemeester
BRT in Amsterdam Kaart achter de burgemeester ▪ sinds 1967 dé kaart van Amsterdam ▪ sinds 2013 uit BRT/Top10NL ▪ jaarlijkse actualiteit ▪ 9-delige wandkaart Amsterdam ▪ basiskaart data.amsterdam.nl ▪ topografische deelkaarten ▪ thematische toepassingen KBKA10 vormgeving Amsterdam BRT/Top10NL vormgeving Kadaster BRT/Top10NL Amsterdamse stijl met binnentuinen uit BGT BRT in Amsterdam ▪ Bebouwing: laag/hoogbouw ▪ Water ▪ Snelweg ▪ OV-infra+stations: trein, metro, tram ▪ Km-raaipalen (snelweg) ▪ Bos, grasland BRT in Amsterdam ▪ Functioneel gebied: Begraafplaats, park ▪ Infra: wegen, verhard/onverhard BRT in Amsterdam ▪ Functioneel gebied: dras, moerasig ▪ Bovenzijde talud BRT in Amsterdam ▪ Functioneel gebied: bedrijfsterrein ▪ Hoogspanningsleiding + mast ▪ Havenlicht BRT in Amsterdam ▪ Politie ▪ Brandweer ▪ Monument ▪ Aanlegsteiger ▪ Water onder wegen = brug BRT in Amsterdam ▪ Kas/warenhuis ▪ Grasland ▪ Bovenzijde talud BRT in Amsterdam ▪ Start-rolbaan BRT in Amsterdam ▪ Terrein: zand ▪ Aanlegsteiger ▪ Groen: bos BRT in Amsterdam ▪ Veel ‘overig terrein’ ▪ Braakliggend plus-info ▪ Bedrijfs/industrie plus-info BRT in Amsterdam ▪ Veel ‘overig terrein’ ▪ Veel ‘grasland’ ▪ Bedrijfs/industrie plus-info BRT in Amsterdam ▪ Veel ‘overig terrein’ ▪ Veel ‘grasland’ ▪ Bedrijfs/industrie Maatwerk kaarten op basis BRT ▪ Vaarverbod i.v.m. corona Maatwerk kaarten op basis BRT ▪ MUPI-kaarten, infohavens Maatwerk kaarten – Verkiezingen Maatwerk kaarten – Oostelijk Havengebied Maatwerk kaarten – Oostelijk Havengebied Maatwerk kaarten – gebiedsteams stadsdeel -

De Drooglegging Van Amsterdam
DE DROOGLEGGING VAN AMSTERDAM Een onderzoek naar gedempt stadswater Jeanine van Rooijen, stageverslag 16 mei 1995. 1 INLEIDING 4 HOOFDSTUK 1: DE ROL VAN HET WATER IN AMSTERDAM 6 -Ontstaan van Amsterdam in het waterrijke Amstelland 6 -De rol en ontwikkeling van stadswater in de Middeleeuwen 6 -op weg naar de 16e eeuw 6 -stadsuitbreiding in de 16e eeuw 7 -De rol en ontwikkeling van stadswater in de 17e en 18e eeuw 8 -stadsuitbreiding in de 17e eeuw 8 -waterhuishouding en vervuiling 9 HOOFDSTUK 2: DE TIJD VAN HET DEMPEN 10 -De 19e en begin 20e eeuw 10 -context 10 -gezondheidsredenen 11 -verkeerstechnische redenen 12 -Het dempen nader bekeken 13 HOOFDSTUK 3: ENKELE SPECIFIEKE CASES 15 -Dempingen in de Jordaan in de 19e eeuw 15 -Spraakmakende dempingen in de historische binnenstad in de 19e eeuw 18 -De bouw van het Centraal Station op drie eilanden en de aanplempingen 26 van het Damrak -De Reguliersgracht 28 -Het Rokin en de Vijzelgracht 29 -Het plan Kaasjager 33 HOOFDSTUK 4: DE HUIDIGE SITUATIE 36 BESLUIT 38 BRONVERMELDING 38 BIJLAGE: -Overzicht van verdwenen stadswater 45 2 Stageverslag Geografie van Stad en Platteland Stageverlener: Dhr. M. Stokroos Gemeentelijk Bureau Monumentenzorg Amsterdam Keizersgracht 12 Amsterdam Cursusjaar 1994/1995 Voortgezet Doctoraal V3.13 Amsterdam, 16 mei 1995 DE DROOGLEGGING VAN AMSTERDAM een onderzoek naar gedempt stadswater Janine van Rooijen Driehoekstraat 22hs 1015 GL Amsterdam 020-(4203882)/6811874 Coll.krt.nr: 9019944 3 In de hier voor U liggende tekst staat het eeuwenoude thema 'water in Amsterdam' centraal. De stad heeft haar oorsprong, opkomst, ontplooiing, haar specifieke vorm en schoonheid, zelfs haar naam te danken aan een constante samenspraak met het water. -

Metro Tram Bus IJ Veren Noordzeekanaal Ponten Van Waar
Van waar naar waar Metro 50 Isolatorweg - Station Sloterdijk - Station Zuid - Station Bijlmer ArenA - Gein 51 Centraal Station - Station Zuid - Amstelveen Westwijk 52 Noord - Centraal Station - Station Zuid 53 Centraal Station - Van der Madeweg - Gaasperplas 54 Centraal Station - Van der Madeweg - Station Bijlmer ArenA - Gein Tra m 2 1 Osdorp De Aker - Leidseplein - Muiderpoortstation 2 Nieuw Sloten - Leidseplein - Centraal Station 3 Flevopark - Muiderpoortstation - Museumplein - Zoutkeetsgracht 4 Station RAI - Rembrandtplein - Centraal Station 5 Amstelveen Stadshart - Station Zuid - Museumplein - Leidseplein - Westergasfabriek 7 Slotermeer - Leidseplein - Weesperplein - Azartplein 11* Surinameplein - Leidseplein - Centraal Station 12 Amstelstation - Museumplein - Leidseplein - Centraal Station 13 Geuzenveld - Westermarkt - Centraal Station 14 Flevopark - Rembrandtplein - Dam - Centraal Station 17 Osdorp Dijkgraafplein - Westermarkt - Centraal Station 19 Station Sloterdijk - Leidseplein - Weesperplein - Diemen Sniep 24 VU medisch centrum - Vijzelgracht - Centraal Station 26 IJburg - Piet Heinkade - Centraal Station Bus 15 Station Sloterdijk - Mercatorplein - Haarlemmermeerstation - Station Zuid 18 Slotervaart - Mercatorplein - Centraal Station 21 Geuzenveld - Bos en Lommer - Staatsliedenbuurt - Centraal Station 22 Muiderpoortstation - Centraal Station - Spaarndammerbuurt - Station Sloterdijk 34 Olof Palmeplein - Station Noord - Banne Buiksloot - Noorderpark - Meeuwenlaan 35 Olof Palmeplein - Noorderpark - Meteorenweg - Molenwijk 36* Olof -
Guía 4: Holanda, Alemania, Nórdicos
Facultad de Arquitectura UDELAR Montevideo | Uruguay GRUPO DE VIAJE 2013 ARQUITECTURA RIFA G´06 EQUIPO DOCENTE Adriana Barreiro Jorge Casaravilla Gustavo Hiriart Pablo Kelbauskas Bernardo Martín Ximena Rodríguez Soledad Patiño Ernesto Spósito MÓDULO 03 GUÍA EUROPA II DOCENTES MÓDULO 03 Bernando Martín Gustavo Hiriart Nota importante: Las Guías de los Grupos de Viaje de la Facultad de Arquitectura de la Universidad de la República son el resultado del trabajo de sucesivos Equipos Docentes Directores y generaciones de estudiantes. En particular, el material contenido en las presentes Guías fue compilado por el Grupo de Viaje Generación 2005 y su Equipo Docente Director del Taller Danza, quienes realizaron su viaje de estudios en el año 2012. Este material ha sido editado y adaptado al proyecto académico del Grupo de Viaje Generación 2006, cuyo viaje de estudios se realizará en el año 2013. Facultad de Arquitectura UDELAR GRUPO DE VIAJE 2012 ARQUITECTURA RIFA G05 EQUIPO DOCENTE Taller Danza Marcelo Danza Lucía Bogliaccini Luis Bogliaccini Diego Capandeguy Marcos Castaings Martín Delgado Andrés Gobba Lucas Mateo Nicolás Newton Natalia Olivera Felipe Reyno Thomas Sprechmann Marcelo Staricco MÓDULO 03 GUÍA EUROPA II DOCENTES MÓDULO 03 Martín Delgado Andrés Gobba Felipe Reyno GRUPO DE TRABAJO Maite Castiñeira Mercedes Cedrés Lucia Cleffi Leticia Dibarboure María Noel Escanlar Carla Firpo Fiorella Galvalisi Pablo Herrera Gabriel Perez Ana Laura Rodriguez Serpa César Sabani HOLANDA DatoS GENERALES: Superficie: 41.528 km² Población: 16.543425 hab Densidad de Población: 488 hab/km² Capital: Amsterdam Idioma: Holandés Religión: Catolicismo (27%), Protestantes (17%), Musulmán (6%). EUROPA | HOLANDA 6 GUÍA DE VIAJE | GENERACIÓN 2006 EUROPA | HOLANDA I. -

Aanvulling Op Het Ontwerpverkeersbesluit Snorfiets Naar De Rijbaan Met Helmpicht, Binnen De Ring A10, Zoals Gepubliceerd in De Staatscourant Van 13 Augustus 2018 Nr
Nr. 50967 6 september STAATSCOURANT 2018 Officiële uitgave van het Koninkrijk der Nederlanden sinds 1814 •Aanvulling op het ontwerpverkeersbesluit snorfiets naar de rijbaan met helmpicht, binnen de Ring A10, zoals gepubliceerd in de Staatscourant van 13 augustus 2018 nr. 45619 Op 13 augustus jl. heeft de gemeente Amsterdam het ontwerpverkeersbesluit voor 'Snorfiets naar de rijbaan met helmplicht' gepubliceerd. De uitwerking van deze maatregel stond voor een aantal fietspaden in dit besluit abusievelijk nog niet genoemd. Dat was het gevolg van het gebruik van een aantal verkeerde kaartdelen. De gemeente vind het belangrijk om een compleet beeld te geven van de impact van de maatregel. Daarom publiceert de gemeente hierbij een aanvullende lijst met (delen) van fietspaden binnen de Ring A10. I. Voor de volgende (delen van) fietspaden geldt het ontwerpverkeersbesluit, zoals gepubliceerd in de Staatscourant van 13 augustus 2018 nr 45619, eveneens: Onder het hoofdstuk Wijk Oost 2 Tekening SNOR-BO-O2-7 • de Wijttenbachstraat, de fietspaden gelegen ter weerszijden van de hoofdrijbaan; • het Linnaeusplantsoen, in beide richtingen; • de Middenweg, tussen de Linnaeuskade en de Wethouder Frankeweg, de fietspaden ter weerszijden van de hoofdrijbaan; • de Celebesstraat, het fietspad gelegen tussen de 1e Atjehstraat en de Balistraat, in beide richtingen; • de Ruyschstraat, het fietspad gelegen aan de evenzijde tussen de Camperstraat en het 's Gravesande- plein, in beide richtingen; • de Ringdijk: 1. tussen de Schollenburgstraat en de Wibautstraat, in beide richtingen; 2. tussen de 1e Ringdijkstraat en de Nobelweg, in beide richtingen; Onder het hoofdstuk Wijk Oost 3 Tekening SNOR-BO-O3-7 • de Cruquiusweg, tussen de Veelaan en de C. -
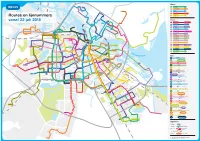
20170627-GVB19-Totaal Lijnennetkaart-Def2
Metro 50 Isolatorweg Gein Molenwijk 35 51 Centraal Station Westwijk Zunderdorp 31 52 Noord Zuid 53 Centraal Station Gaasperplas Holysloot 30 Routes en lijnnummers 54 Centraal Station Gein BovenIJ Ziekenhuis Station Noord Tram vanaf 22 juli 2018 30 31 34 37 38 Ataturk 1 Osdorp de Aker Muiderpoortstation Station Noord 52 NDSM 2 Centraal Station Nieuw Sloten 38 Buiksloter- Houthavens meerplein Klaprozenweg NDSM 48 VEER Flevopark Zoutkeetsgracht 248 3 DISTELWEG VEER 36 35 50 4 Centraal Station Station RAI HOUTHAVEN Olof Palmeplein VEER Isolatorweg Westergasfabriek Amstelveen Stadshart Waterlandplein 5 Station Sloterdijk 231 Abberdaan 7 Slotermeer Azartplein 15 22 36 Zoutkeetsgracht Noorderpark 61 69 231 3 Station 19 Station Sloterdijk Sloterdijk 11 Centraal Station Surinameplein Meeuwenlaan 34 Westerpark 12 Centraal Station Amstelstation 5 Doorgaande Westergasfabriek lijnen Centraal Station 22 48 13 Centraal Station Geuzenveld BUIKSLOTER Buiksloter- OOSTVEER 13 17 14 18 WEGVEER wegveer 21 51 11 2 4 248 52 IJPLEIN Centraal Station Flevopark 12 24 VEER 14 53 Geuzenveld 54 26 13 De Marnixplein Vlugtlaan Centraal Station Osdorp Dijkgraafplein Bos en Nieuwezijds Kolk 17 KNSM Eiland Lommerplein Azartplein 7 65 Geuzenveld 21 Slotermeerlaan 19 Station Sloterdijk Diemen (Sniep) Erasmuspark Jan van Galenstraat Slotermeer Dam 24 Centraal Station VU Medisch Centrum Westermarkt 7 Nieuwmarkt 48 Borneo Eiland Mercatorplein Adm. de Centraal Station IJburg Ruyterweg 26 Spui Rokin Waterlooplein Flevopark Kinkerstraat/ Rembrandtplein Bilderdijkstraat 14 3 Muntplein -

Bekende En Onbekende Namen Van Bruggen, Sluizen En Tunnels Binnen De Gemeente Amsterdam
Bekende en onbekende namen van bruggen, sluizen en tunnels binnen de Gemeente Amsterdam. Aalmoezeniersbrug ³ BRU0068 Vaste brug Nabij gelegen gerechtshof aan de Prinsengracht was een voormalig Aalmoezeniersweeshuis Aandammerbrug ² BRU058P P-Brug In de Poppendammergouw over de sloot die de Holysloter met het Bozenmeertje verbindt. Deze ophaalbrug in stadsdeel Noord is genoemd naar de Aandammergouw, waarin ze ligt, gezien vanuit de gemeente Broek in Waterland. De Aandammerbrug is 1 van de kleinste bruggen van Amsterdam, het was oorspronkelijk een houten brug gebouwd op zes jukken. Zij werd vervangen door een zogenaamde hoge zijl. Abel Tasmanbrug ³ BRX0118 Basculebrug, administratief Deze naam verwijst ook naar de Tasman straat en wordt ook wel de Tasmanbrug genoemd. Zie ook BRU0346 Afslagtunnel Gein-lijn ² BRU1616 Tunnel Genoemd naar het metrostation. Akerschutsluis ¹ SLU0102 Sluis Officiële naam voor deze schutsluis Aluminiumbrug ² BRU0222 Ophaalbrug Deze ophaalbrug wordt zo genoemd, omdat in 1956 het val (brugdek) van deze brug (als eerste in Nederland) in aluminium werd uitgevoerd. Een andere naam was Dwingerbrug, naar het naastgelegen bolwerk "Swijght Utrecht". BRX0113 Ambachtsbrug ³ BRX0107 Vaste brug, administratief Genoemd naar de nabij gelegen ambachtsschool, zie ook BRU0358 Amstelbrug ² BRX0077 Vaste brug, administratief Dit is een oude naam voor de Hoge Sluis, de Amstelbrug is genoemd naar het water dat zij overspant, voor de werkelijke naam en een verklaring van deze naam kijk bij BRU0246. Amstelschutsluis ¹ SLU0101 Sluis Officiële naam voor deze schutsluis. De enige sluizen in de Amstel die nog te zien zijn, liggen ter hoogte van Carre, zij dateren uit 1673 (ontwerp van Joh. Hudde) en hadden oorspronkelijk tot taak het Ijwater uit de Amstel te houden. -

Dorint · Airport-Hotel · Amsterdam
Welcome. Made by Dorint Airport-Hotel Amsterdam Only five kilometers away from Amsterdam Schiphol airport you will find a conference hotel that will perfectly meet your expectations: our Dorint Airport-Hotel Amsterdam. The newly designed hotel includes 222 rooms and suites, 10 meeting rooms of variable sizes and five conference suites, all featuring air conditioning, daylight and modern audio-visual equipment. Another plus is the easy access by private and public transport. Amsterdam city centre is only 10 km, the motorways A 4 and A 9 are 1 km away. Schiphol airport and train station can be reached within a few minutes with our free shuttle. Accommodation June 2014 ■ 222 modern and spacious air-conditioned rooms incl. 11 Executive rooms and 13 suites ■ 10 conference rooms and 5 conference suites, all with air-conditioning and daylight ■ Wi-Fi inclusive ■ Free shuttle service from and to Schiphol airport ■ Parking facilities at the hotel (outdoor) with 130 parking spaces (charges apply) Food & drinks ■ Lovely stylish restaurant serving international and regional cuisine, seating for 140 guests ■ Cosy lobby bar ■ 24-hrs room service available ■ Kiosk in the hotel lobby for drinks and snacks Social Programs ■ Bike rental (charges apply) ■ Windmill and museum: “De Molen van Sloten” / Kuiperijmuseum ■ Amsterdam city center with many museums ■ Shopping in Amsterdam, Hoofddorp, Amstelveen or Schiphol airport Distances ■ Amsterdam Schiphol airport: 5 km ■ Highway A 4 (Schiphol – Den Haag): 1 km ■ Highway A 9 (Haarlem – Amstelveen): 1 km ■ Railway station Amsterdam Schiphol: 5 km ■ Amsterdam city center: 10 km ■ Haarlem: 14 km ■ Utrecht: 44 km ■ Den Haag: 53 km Dorint Meeting Service Regardless of what kind of event you plan, plan it with us on tel. -

Voorloopige Lijst Der Monumenten in De Gemeente Amsterdam
VOORLOOPIGE LIJST DER MONUMENTEN IN DE GEMEENTE AMSTERDAM, VOORLOOPIGE LIJST DER NEDERLANDSCHE MONU- MENTEN VAN GESCHIEDENIS IR EN KUNST g, DEEL V, ir DE GEMEENTE AMSTERDAM OPGEMAAKT EN UITGEGEVEN DOOR AFDEELING A DER RIJKSCOMMISSIE VOOR DE MONUMENTENZORG INGESTELD BIJ KONINKLIJK BESLUIT VAN 10 MEI 1918, N o, 66 I S GRAVENHAGE - ALGEMEENE LANDSDRUKKERIJ - 1928 VERKRIJGBAAR BIJ A, OOSTHOEK TE UTRECHT VOORWOORD. Dit stuk verschijnt als het tweede van deel V van de „Voorloopige lijst der Nederlandsche monumenten van geschiedenis en kunst'', Het eerste stuk van dit deel, gewijd aan de provincie Noord-Holland, uit- gezonderd Amsterdam, zag in 1921 het licht, 1) De gegevens voor het thans verschijnende stuk zijn in de jaren 1919— 1925 door den SECRETARIS van Afdeeling A der Rijkscommissie voor de Monumentenzorg Dr, E, J. HASLINGHUIS, bijeengebracht nit de topogra- fische en historische literatuur over de stad Amsterdam, waarbij VAN ARKEL en WEISSMAN's „Noord-Hollandsche Oudheden" (1891-1905) een geschikten grondslag vormde, Aangezien de XVIIIe-eeuwsche bouwkunst in dit werk niet tot haar recht komt en de stelselmatige beschrijving van particuliere binnenhuizen, van schilderijen, van kerkzilver en liturgisch gerei e, d, buiten het werkplan der genoemde schrijvers viel, moest het materiaal der „Oudheden" aanmerkelijk worden uitgebreid, Voor de woonhuisgevels kon verder dankbaar gebruik worden gemaakt van een 1 apport in 1920 door den heer C, VISSER aan de vereeniging „Hendrik de Keyser" uitgebracht. De aldus verzamelde stof bracht men voorloopig op schrift en be- werkte ze op de volgende wijze: 1. Nadat eene „subcommissie voor de inventarisatie der monu- menten van Amsterdam" was gevormd, bestaande uit de Afdeelings- leden J. -

De Schoonheid Van Amsterdam
De Schoonheid van Amsterdam Gemeente Amsterdam Bijlage, 2016 DE SCHOONHEID VAN AMSTERDAM 2016: BIJLAGE PAGINA 1 De Schoonheid van Amsterdam Bijlage Gemeente Amsterdam 2016 Bijlage 1 Hoe werkt welstand? 3 INHOUD Bijlage 2 Algemene welstandscriteria 11 Bijlage 3 Begrippen 17 Bijlage 4 Transformatiegebieden 29 Bijlage 5 Reclame 37 Bijlage 6 Kaarten 43 DE SCHOONHEID VAN AMSTERDAM 2016: BIJLAGE PAGINA 1 DE SCHOONHEID VAN AMSTERDAM 2016: BIJLAGE PAGINA 2 Hoe werkt welstand? BIJLAGE 1 DE SCHOONHEID VAN AMSTERDAM 2016: BIJLAGE PAGINA 3 DE SCHOONHEID VAN AMSTERDAM 2016: BIJLAGE PAGINA 4 Bijlage 1 | Hoe werkt welstand? TOESTEMMING VRAGEN OM TE Excessenregeling BOUWEN Ook bij vergunningsvrij bouwen gel- HOE WERKT den de regels met betrekking tot on- Aanvraag van een omgevings der meer veiligheid en gezondheid WELSTAND? vergunning uit het Bouwbesluit en het buren- In hoofdstuk 1 van deze nota staat recht zoals vastgelegd in het Bur- Bijlage 1 beschreven hoe welstand werkt gerlijk Wetboek. Bouwwerken die en waarom voor de meeste sloop-, zonder vergunning mogen worden bouw- en verbouwplannnen een om- gebouwd of zijn gebouwd, zijn ook gevingsvergunning moet worden niet helemaal vrij van welstandstoe- aangevraagd. Deze aanvraag zal zicht en moeten aan minimale wel- door de gemeente op verschillende standseisen voldoen. Ze mogen ‘niet punten beoordeeld worden. Er wordt in ernstige mate in strijd zijn met re- getoetst of een plan voldoet aan de delijke eisen van welstand’. Als dit eisen uit het Bouwbesluit, zoals vei- wel het geval is, is sprake van een ligheid, gezondheid of energiezui- ‘exces’. Wanneer er sprake is van nigheid. Ook wordt gekeken of het een exces is omschreven in de ‘ex- bouwplan in het bestemmingsplan cessenregeling’ in hoofdstuk 2.5 van past. -

GVB Bussen, Trams En Metro's
Metro 50 Isolatorweg Gein Molenwijk 35 51 Centraal Station Westwijk Zunderdorp 31 52 Noord Zuid 53 Centraal Station Gaasperplas Holysloot 30 Routes en lijnnummers 54 Centraal Station Gein BovenIJ Ziekenhuis Station Noord Tram vanaf 22 juli 2018 30 31 34 37 38 Ataturk 1 Osdorp de Aker Muiderpoortstation Station Noord 52 NDSM 2 Centraal Station Nieuw Sloten 38 Buiksloter- Houthavens meerplein Klaprozenweg NDSM 48 VEER Flevopark Zoutkeetsgracht 248 3 DISTELWEG VEER 36 35 50 4 Centraal Station Station RAI HOUTHAVEN Olof Palmeplein VEER Isolatorweg Westergasfabriek Amstelveen Stadshart Waterlandplein 5 Station Sloterdijk 231 Abberdaan 7 Slotermeer Azartplein 15 22 36 Zoutkeetsgracht Noorderpark 61 69 231 3 Station 19 Station Sloterdijk Sloterdijk 11 Centraal Station Surinameplein Meeuwenlaan 34 Westerpark 12 Centraal Station Amstelstation 5 Westergasfabriek Centraal Station 13 Centraal Station Geuzenveld BUIKSLOTER Buiksloter- OOSTVEER 13 17 14 18 WEGVEER wegveer 21 51 11 2 4 248 52 IJPLEIN Centraal Station Flevopark 12 24 VEER 14 53 Geuzenveld 54 26 13 Marnixplein Centraal Station Osdorp Dijkgraafplein Bos en Nieuwezijds Kolk 17 KNSM Eiland Lommerplein Azartplein 7 65 Geuzenveld 21 Slotermeerlaan 19 Station Sloterdijk Diemen (Sniep) Erasmuspark Jan van Galenstraat Slotermeer Dam 24 Centraal Station VU Medisch Centrum Westermarkt 7 Nieuwmarkt 48 Borneo Eiland Mercatorplein Adm. de Centraal Station IJburg Ruyterweg 26 Spui Rokin Waterlooplein Flevopark Kinkerstraat/ Rembrandtplein Bilderdijkstraat 14 3 Muntplein Artis Sloterplas Postjesweg