Proquest Dissertations
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The BG News April 15, 1999
Bowling Green State University ScholarWorks@BGSU BG News (Student Newspaper) University Publications 4-15-1999 The BG News April 15, 1999 Bowling Green State University Follow this and additional works at: https://scholarworks.bgsu.edu/bg-news Recommended Citation Bowling Green State University, "The BG News April 15, 1999" (1999). BG News (Student Newspaper). 6484. https://scholarworks.bgsu.edu/bg-news/6484 This work is licensed under a Creative Commons Attribution-Noncommercial-No Derivative Works 4.0 License. This Article is brought to you for free and open access by the University Publications at ScholarWorks@BGSU. It has been accepted for inclusion in BG News (Student Newspaper) by an authorized administrator of ScholarWorks@BGSU. ■" * he BG News Women rally to 'take back the night' sexual assault. istration vivors, they will be able to relate her family. By WENDY SUTO Celesta Haras/ti, a resident of buildings, rain to parts of her story, Kissinger "The more I tell my story, the The BG News BG and a W4W member, said the or shine. The said. less shame and guilt I feel," Kissinger said. "For my situa- Women (and some men) will rally is about issues that are con- keynote "When I decided to disclose tion, I'm glad I didn't tell my take to the streets tonight, pro- sidered taboo by society, such as speaker, my sexual abuse to my family, I parents right away because I claiming a public statement in an rape and incest. She has attended Kendel came out of the closet complete- think it would have been a worse attempt to "Take Back the Night" several TBTN marches at the Kissinger, a ly," Kissinger said. -
![[Japan] SALA GIOCHI ARCADE 1000 Miglia](https://docslib.b-cdn.net/cover/3367/japan-sala-giochi-arcade-1000-miglia-393367.webp)
[Japan] SALA GIOCHI ARCADE 1000 Miglia
SCHEDA NEW PLATINUM PI4 EDITION La seguente lista elenca la maggior parte dei titoli emulati dalla scheda NEW PLATINUM Pi4 (20.000). - I giochi per computer (Amiga, Commodore, Pc, etc) richiedono una tastiera per computer e talvolta un mouse USB da collegare alla console (in quanto tali sistemi funzionavano con mouse e tastiera). - I giochi che richiedono spinner (es. Arkanoid), volanti (giochi di corse), pistole (es. Duck Hunt) potrebbero non essere controllabili con joystick, ma richiedono periferiche ad hoc, al momento non configurabili. - I giochi che richiedono controller analogici (Playstation, Nintendo 64, etc etc) potrebbero non essere controllabili con plance a levetta singola, ma richiedono, appunto, un joypad con analogici (venduto separatamente). - Questo elenco è relativo alla scheda NEW PLATINUM EDITION basata su Raspberry Pi4. - Gli emulatori di sistemi 3D (Playstation, Nintendo64, Dreamcast) e PC (Amiga, Commodore) sono presenti SOLO nella NEW PLATINUM Pi4 e non sulle versioni Pi3 Plus e Gold. - Gli emulatori Atomiswave, Sega Naomi (Virtua Tennis, Virtua Striker, etc.) sono presenti SOLO nelle schede Pi4. - La versione PLUS Pi3B+ emula solo 550 titoli ARCADE, generati casualmente al momento dell'acquisto e non modificabile. Ultimo aggiornamento 2 Settembre 2020 NOME GIOCO EMULATORE 005 SALA GIOCHI ARCADE 1 On 1 Government [Japan] SALA GIOCHI ARCADE 1000 Miglia: Great 1000 Miles Rally SALA GIOCHI ARCADE 10-Yard Fight SALA GIOCHI ARCADE 18 Holes Pro Golf SALA GIOCHI ARCADE 1941: Counter Attack SALA GIOCHI ARCADE 1942 SALA GIOCHI ARCADE 1943 Kai: Midway Kaisen SALA GIOCHI ARCADE 1943: The Battle of Midway [Europe] SALA GIOCHI ARCADE 1944 : The Loop Master [USA] SALA GIOCHI ARCADE 1945k III SALA GIOCHI ARCADE 19XX : The War Against Destiny [USA] SALA GIOCHI ARCADE 2 On 2 Open Ice Challenge SALA GIOCHI ARCADE 4-D Warriors SALA GIOCHI ARCADE 64th. -
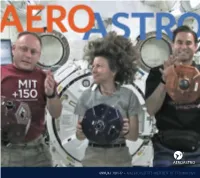
Aeroastro-2011-12.Pdf
ANNUAL 2011-12 • MASSACHUSETTS INSTITUTE OF TECHNOLOGY Editors Department Head Associate Head Editor & Director of Communications Jaime Peraire Karen Willcox William T.G. Litant [email protected] [email protected] [email protected] AeroAstro is published annually by the Massachusetts Institute of Technology Department of Aeronautics and Astronautics, 33-240, 77 Massachusetts Avenue, Cambridge, Massachusetts 02139, USA. http://www.mit.aero AeroAstro No. 9, July 2012 ©2012 The Massachusetts Institute of Technology. All rights reserved. Except where noted, photographs by William Litant/MIT DESIGN Opus Design www.opusdesign.us Cover: Alumni astronauts (from left) Mike Fincke (AeroAstro, BSc ’89), Cady Coleman (ChemE, BSc ’83), and Greg Chamitoff (AeroAstro, PhD ’82), wearing MIT 150 anniversary t-shirts, send video greetings from the International Space Station to high school students around the world participating in AeroAstro’s 2011 Zero Robotics competition. Each is accom- panied by a Space System’s Lab SPHERE microsatellite. For more on Zero Robotics and SPHERES, turn to page 25 (Video grab via NASA). Cert no. XXX-XXX-000 THESE ARE EXCITING TIMES FOR AEROASTRO. Our research funding has risen by 40 percent over the past three years: there are more than 170 research projects in our labs and centers repre- senting $28 million in expenditures by the Department of Defense, NASA, other federal agencies and departments, and the aerospace industry. Our incoming sophomore class size is up by 48 percent over last year. Our faculty now includes a former secretary to the Air Force, a former astronaut, a former NASA associate administrator, a former USAF chief scientist, nine National Academy of Engineering members, nine Amer- ican Institute of Aeronautics and Astronautics Fellows, two Guggenheim Indeed, we have a number of great projects and initiatives ramping Medal recipients, and two AIAA Reed Aeronautics Award recipients. -

IMPROVE Nephelometer Sops.Pdf
QUALITY ASSURANCE/QUALITY CONTROL DOCUMENTATION SERIES TITLE SITE SELECTION FOR OPTICAL MONITORING EQUIPMENT (IMPROVE PROTOCOL) TYPE STANDARD OPERATING PROCEDURE NUMBER 4050 DATE FEBRUARY 1994 AUTHORIZATIONS TITLE NAME SIGNATURE ORIGINATOR Ivar J. Rennat PROJECT MANAGER James H. Wagner PROGRAM MANAGER David L. Dietrich QA MANAGER Gloria S. Mercer OTHER REVISION HISTORY REVISION CHANGE DATE AUTHORIZATIONS NO. DESCRIPTION 1.0 Add responsibilities and equipment. October 1996 Number 4050 Revision 1.0 Date OCT 1996 Page i of i TABLE OF CONTENTS Section Page 1.0 PURPOSE AND APPLICABILITY 1 2.0 RESPONSIBILITIES 2 2.1 Program Manager 2 2.2 Project Manager 2 2.3 Field Specialist 2 2.4 Local (On-Site) Contact 3 3.0 REQUIRED EQUIPMENT AND MATERIALS 3 4.0 METHODS 4 4.1 Nephelometer Site Selection Methods 4 4.1.1 Locating Potential Sites 4 4.1.2 Reviewing and Selecting Potential Sites 4 4.1.3 Finalizing Site Selection 4 4.2 Transmissometer Site Selection Methods 5 4.2.1 Siting Criteria 5 4.2.2 Locating Potential Sites 5 4.2.3 Reviewing and Selecting Potential Sites 5 4.2.4 Finalizing Site Selection 5 Number 4050 Revision 1.0 Date OCT 1996 Page 1 of 6 1.0 PURPOSE AND APPLICABILITY This standard operating procedure (SOP) outlines site selection criteria for optical monitoring instruments operated according to IMPROVE Protocol. Documented site selection criteria and procedures assure consistent, quality data at sites that exhibit most or all of the following characteristics: • Be located in an area representative of the air mass to be monitored • Be -

\0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 X 1 Kampf ... \0-9\1, 2, 3
... \0-9\0 and X ... \0-9\0 Grad Nord ... \0-9\0013 ... \0-9\007 Car Chase ... \0-9\1 x 1 Kampf ... \0-9\1, 2, 3 ... \0-9\1,000,000 ... \0-9\10 Pin ... \0-9\10... Knockout! ... \0-9\100 Meter Dash ... \0-9\100 Mile Race ... \0-9\100,000 Pyramid, The ... \0-9\1000 Miglia Volume I - 1927-1933 ... \0-9\1000 Miler ... \0-9\1000 Miler v2.0 ... \0-9\1000 Miles ... \0-9\10000 Meters ... \0-9\10-Pin Bowling ... \0-9\10th Frame_001 ... \0-9\10th Frame_002 ... \0-9\1-3-5-7 ... \0-9\14-15 Puzzle, The ... \0-9\15 Pietnastka ... \0-9\15 Solitaire ... \0-9\15-Puzzle, The ... \0-9\17 und 04 ... \0-9\17 und 4 ... \0-9\17+4_001 ... \0-9\17+4_002 ... \0-9\17+4_003 ... \0-9\17+4_004 ... \0-9\1789 ... \0-9\18 Uhren ... \0-9\180 ... \0-9\19 Part One - Boot Camp ... \0-9\1942_001 ... \0-9\1942_002 ... \0-9\1942_003 ... \0-9\1943 - One Year After ... \0-9\1943 - The Battle of Midway ... \0-9\1944 ... \0-9\1948 ... \0-9\1985 ... \0-9\1985 - The Day After ... \0-9\1991 World Cup Knockout, The ... \0-9\1994 - Ten Years After ... \0-9\1st Division Manager ... \0-9\2 Worms War ... \0-9\20 Tons ... \0-9\20.000 Meilen unter dem Meer ... \0-9\2001 ... \0-9\2010 ... \0-9\21 ... \0-9\2112 - The Battle for Planet Earth ... \0-9\221B Baker Street ... \0-9\23 Matches .. -

Genetic Testing and the Future of Cerebral Palsy Malpractice Cases
What’s the VERDICT? Genetic testing and the future of cerebral palsy malpractice cases Would genetic testing have prevented this lawsuit? Joseph S. Sanfilippo, MD, MBA, and Steven R. Smith, MS, JD CASE Mixed CP diagnosed at age 6 months After learning that the statute of limitations was to run out in the near future, the parents of a 17-year-old with cerebral palsy (CP) initi- ated a lawsuit. At the time of her pregnancy, the mother (G2P2002) was age 39 and first sought prenatal care at 14 weeks. Her past medical history was largely non- contributory to her current pregnancy, except for that she had hypothyroidism that was being treated with levothyroxine. She also had a his- IN THIS tory of asthma, but had had no acute episodes ARTICLE for years. During the course of the pregnancy there was evidence of polyhydramnios; her initial Types of cerebral thyroid studies were abnormal (thyroid-stimulat- palsy ing hormone levels, 7.1 mIU/L), in part due to page 41 lack of adherence with prescribed medications. She was noted to have elevated blood pressure (BP) 150/100 mm Hg but no proteinuria, with BP Legal monitoring during her last trimester. considerations page 42 Dr. Sanfilippo is Professor, Department Avoiding of Obstetrics, Gynecology, and Reproductive Sciences, University of malpractice claims Pittsburgh, and Director, Reproductive page 46 Endocrinology and Infertility, at Magee-Womens Hospital, Pittsburgh, Pennsylvania. He also serves on the OBG MANAGEMENT Board of Editors. Mr. Smith is Professor Emeritus and Dean Emeritus at California Western School of Law, San Diego, California. -

Basic Concepts in Turbomachinery Grant Ingram
BASIC CONCEPTS IN TURBOMACHINERY GRANT INGRAM DOWNLOAD FREE TEXT BOOKS AT BOOKBOON.COM Grant Ingram Basic Concepts in Turbomachinery Download free books at BookBooN.com 2 Basic Concepts in Turbomachinery © 2009 Grant Ingram & Ventus Publishing ApS ISBN 978-87-7681-435-9 Download free books at BookBooN.com 3 Basic Concepts in Turbomachinery Contents Contents 1 Introduction 16 1.1 How this book will help you 17 1.2 Things you should already know 17 1.3 What is a Turbomachine? 17 1.4 A Simple Turbine 18 1.5 The Cascade View 19 1.6 The Meridional View 23 1.7 Assumptions used in the book 23 1.8 Problems 24 2 Relative and Absolute Motion 25 2.1 1D Motion 26 2.2 2D Motion 27 2.3 Velocity Triangles in Turbomachinery 28 2.4 Velocity Components 30 2.5 Problems 33 3 Simple Analysis of Wind Turbines 35 3.1 Aerofoil Operation and Testing 38 3.2 Wind Turbine Design 41 3.3 Turbine Power Control 44 WHAt‘s missing in this equaTION? You could be one of our future talents Please click the advert MAERSK INTERNATIONAL TECHNOLOGY & SCIENCE PROGRAMME Are you about to graduate as an engineer or geoscientist? Or have you already graduated? If so, there may be an exciting future for you with A.P. Moller - Maersk. www.maersk.com/mitas Download free books at BookBooN.com 4 Basic Concepts in Turbomachinery Contents 3.4 Further Reading 44 3.5 Problems 45 4 Different Turbomachines and Their Operation 46 4.1 Axial Flow Machines 47 4.2 Radial and Centrifugal Flow Machines 47 4.3 Radial Impellers 49 4.4 Centrifugal Impellers 52 4.5 Hydraulic Turbines 54 4.6 Common Design -

National Camping School’S Annual Theme Program Experiments
2021 Weird Science National Resource Book Camping School Inside this Issue: 2021 FUN! Setting the tone for FUN! Camp Station Location Names Gathering Activities Prayers Opening & Closing Ceremonies Skits Cheers/Applauses Jokes/Run-ons Songs Audience Participation Games & Activities “Weird Science” Crafts National Camping School’s Annual Theme Program Experiments Each year a theme-related resource booklet is STEM produced and distributed through the Cub Scouting National Camp Schools. Snack Ideas The material provided is designed to be used Theme Related Ideas in the districts and councils presenting Cub Scout camping activities. Clipart Upcoming Themes Welcome! The material in this resource book is designed to serve your district or council in providing tremendous Cub Scout day camping events! Many resources were used to compile the information you will find in this booklet. THANK YOU to the leaders who sent in ideas and suggestions and THANK YOU to those who contributed to the resources used. We could not have done it without you!!! We appreciate your help and all that you do for our scouts and day camp!! WEIRD SCIENCE - What experimental fun you will have with this theme! Learn about what is in a scientific laboratory, the why and how things work and all about peculiar and fun experiments. Go outdoors and learn about the world we live in and how science plays a part in all of it. Your adventures may keep you in the lab or take you into the field where investigations and experiments are taking place. Whatever you do, make it fun and memorable for the Cub Scouts and leaders attending! All materials in this book reflect the high standards of the BSA. -

Chapter 1—Introduction
NOTES CHAPTER 1—INTRODUCTION 1. See Juan Flores, “Rappin’, Writin’ & Breakin,’” Centro, no. 3 (1988): 34–41; Nelson George, Hip Hop America (New York: Viking, 1998); Steve Hager, Hip Hop: The Illustrated History of Breakdancing, Rapping and Graffiti (New York: St. Martin’s Press, 1984); Tricia Rose, Black Noise: Rap Music and Black Culture in Contemporary America (Hanover, NH: Wesleyan University Press, 1994); David Toop, The Rap Attack 2: African Rap to Global Hip Hop (London: Serpent’s Tail, 1991). 2. Edward Rodríguez, “Sunset Style,” The Ticker, March 6, 1996. 3. Carlito Rodríguez, “The Young Guns of Hip-Hop,” The Source 105 ( June 1998): 146–149. 4. Clyde Valentín, “Big Pun: Puerto Rock Style with a Twist of Black and I’m Proud,” Stress, issue 23 (2000): 48. 5. See Juan Flores, Divided Borders: Essays on Puerto Rican Identity (Hous- ton: Arte Público Press, 1993); Bonnie Urciuoli, Exposing Prejudice: Puerto Rican Experiences of Language, Race and Class (Boulder, CO: West- view Press, 1996). 6. See Manuel Alvarez Nazario, El elemento afronegroide en el español de Puerto Rico (San Juan: Instituto de Cultura Puertorriqueña,1974); Paul Gilroy, The Black Atlantic: Modernity and Double Consciousness (Cam- bridge, MA: Harvard University Press, 1993); Marshall Stearns, The Story of Jazz (Oxford: Oxford University Press, 1958); Robert Farris Thompson, “Hip Hop 101,” in William Eric Perkins, ed., Droppin’ Sci- ence: Critical Essays on Rap Music and Hip Hop Culture (Philadelphia: Temple University Press, 1996), pp. 211–219; Carlos “Tato” Torres and Ti-Jan Francisco Mbumba Loango, “Cuando la bomba ñama...!:Reli- gious Elements of Afro-Puerto Rican Music,” manuscript 2001. -

QA Handbook for Air Pollution Measurement Systems
Quality Assurance Handbook for Air Pollution Measurement Systems Volume II Ambient Air Quality Monitoring Program Page Intentionally Left Blank EPA-454/B-17-001 January 2017 Quality Assurance Handbook for Air Pollution Measurement Systems Volume II Ambient Air Quality Monitoring Program U.S. Environmental Protection Agency Office of Air Quality Planning and Standards Air Quality Assessment Division RTP, NC 27711 QA Handbook Volume II January 2017 Contents Section Page Revision Date Contents iv FINAL 01/17 Figures vi FINAL 01/17 Tables vii FINAL Acknowledgments viii FINAL 01/17 Acronyms and Abbreviations ix FINAL 01/17 0. Introduction FINAL 01/17 0.1 Intent of the Handbook 1/3 0.2 Use of Terms Shall, Must, Should, May 2/3 0.3 Use of Footnotes 2/3 0.4 Handbook Review and Distribution 2/3 PROJECT MANAGEMENT 1. Program Background FINAL 01/17 1.1 Ambient Air Quality Monitoring Network 1/12 1.2 The EPA Quality System Requirements 6/12 1.3 The Ambient Air Monitoring Program Quality System 8/12 2. Program Organization FINAL 01/17 2.1 Organization Responsibilities 1/7 2.2 Lines of Communication 6/7 3. Data Quality Objectives FINAL 01/17 3.1 The DQO Process 3/7 3.2 Ambient Air Quality DQOs 4/7 3.2 Measurement Quality Objectives 5/7 4. Personnel Qualification and Training FINAL 01/17 4.1 Personnel Qualifications 1/3 4.2 Training 2/3 5. Documentation and Records FINAL 01/17 5.1 Management and Organization 2/9 5.2 Site Information 3/9 5.3 Environmental Data Operations 3/9 5.4 Raw Data 8/9 5.5 Data Reporting 8/9 5.6 Data Management 9/9 5.7 Quality Assurance 9/9 MEASUREMENT ACQUISITION 6. -

Sunflower 05-01-1973 (7.555Mb)
was in honor of the first pres nA 4uii04t la ii lUi^eeJ^^,n(L ident of Fairmouni College, Dr, N.J, Morrison. The columns were formerly located at the front ol lh(! onginal Carnegie Library Colmniis dedicated, lane named There werr* originally eight I olumns, but only ihrer; will ni)w About fifty alumni and guests Spring Reunion last weekend stand on the northeast loiner ol were on hand for the dedication honoring the classes ol '23, ‘28, 1 7 and Fairmount. of the Morrison columns and the '33, '43. '48. '53 and '63. The (olurnns have not yet naming of Isely Lane on campus. The dedication of the relo been erected on thi' site, dur; to The dedications were part of the cation of the Morrison columns bad weather Morrison was instrumental irr securing the $40,n()() Andrew Carnegie conlnbulion to es tahlish thr* library Eleven years in construction, the cornerstone of the new Carnegie I ibrary was laid on March 10, 1908, The library was later renamed Mor rison Library. The 1908 cornerstone was recently opened when construc tion began on the new McKnight Art Building and the old library was torn down. A new cornerstone was laid Saturday where the columns will be located. This is to be opened on the 100th anniversary of Fair mount College in 1995 The street that winds around the back of the CAC, McKinley, and Jardine was named Isely Lane Saturday. The street is named in honor of Dean W.H. Isely, who served with Morrison in the beginning AS they stood originally. -

Or Zero-Emission Multiple-Unit Feasibility Study
Low- or Zero-Emission Multiple-Unit Feasibility Study FEASIBILITY REPORT December 30, 2019 Prepared for: San Bernardino County Transportation Authority 1170 W. 3rd Street, 2nd Floor San Bernardino, CA 92410 Prepared by: Center for Railway Research and Education Eli Broad College of Business Michigan State University www.railway.broad.msu.edu 3535 Forest Road Lansing, MI 48910 USA Birmingham Centre for Railway Research and Education University of Birmingham Edgbaston Birmingham B15 2TT United Kingdom www.railway.bham.ac.uk Authors: Stephen Kent - BCRRE Raphael Isaac - MSU CRRE Nick Little - MSU CRRE Andreas Hoffrichter, PhD - MSU CRRE Executive Summary The San Bernardino County Transportation Authority (SBCTA) is adding the Arrow railway service in the San Bernardino Valley, between San Bernardino and Redlands. SBCTA aims to improve air quality with the introduction of zero-emission rail vehicle technology by procuring a new zero-emission multiple unit (ZEMU) train and converting one of the diesel multiple unit (DMU) trains that will be used to provide Arrow service. Using a Transit and Intercity Rail Capital Program (TIRCP) grant, SBCTA will demonstrate low- or, ideally, zero-emission rail service on the Arrow route. The ZEMU is expected to be in service by 2024 and demonstrate low- or zero-emission railway motive power technology for similar passenger rail service in California as well as a possible technology transfer platform for other railway services. SBCTA commissioned the Center for Railway Research and Education (CRRE) at Michigan State University (MSU) in collaboration with the Birmingham Centre for Railway Research and Education (BCRRE) at the University of Birmingham, United Kingdom, to assist with the comparison of low- and zero-emission technology suitable for railway motive power applications.