DOCSLIB.ORG

1.1 Radian and Degree Measure

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1.1 Radian and Degree Measure 1.1 RADIAN AND DEGREE MEASURE Copyright © Cengage Learning. All rights reserved. Angles The starting position of the ray is the initial side of the angle, and the position after rotation is the terminal side. Angle The endpoint of the ray is the vertex of the angle. Angles When the origin is the vertex and the initial side lies on the positive x-axis, the angle is in standard position. Angles Positive angles - counterclockwise Negative angles - clockwise Radian Measure The measure of an angle is determined by the amount of rotation from the initial side to the terminal side. One way to measure angles is in radians. To define a radian, you can use a central angle of a circle, one whose vertex is the center of the circle. Arc length = radius when = 1 radian Radian Measure Definition of Radian One radian is the measure of a central angle θ that intercepts an arc, s, equal in length to the radius, r, of a circle. 푠 휃 = 푟 휃 is measured in radians Since the circumference of a circle is 2 r, it follows that a central angle of one full revolution corresponds to an arc length of s = 2 r. Radian Measure Since 2 6.28, there are just over six radius lengths in a full circle. Radian Measure Since one full revolution is 2 Radian Measure These are additional common angles. What Quadrant do the following angles lie in? 휋 a) 5 11휋 b) 8 휋 c) − 4 Radian Measure Two angles are coterminal if they have the same initial and terminal sides. To find coterminal angles, we add or subtract multiples of 2. A given angle has infinitely many coterminal angles. For instance, = / 6 is coterminal with 휋 + 2푛휋 6 where n is an integer. Example 1 – Sketching and Finding Coterminal Angles For the positive angle 13 / 6, we can subtract 2 to obtain a coterminal angle Example 1 – Sketching and Finding Coterminal Angles cont’d For the negative angle –2 / 3, add 2 to obtain a coterminal angle Determine two coterminal angles (one positive, one negative) Radian Measure Two positive angles and are complementary if their sum is / 2. Two positive angles are supplementary if their sum is . Complementary angles Supplementary angles Degree Measure A second way to measure angles is in terms of degrees, denoted by the symbol . Degree Measure A full revolution corresponds to 360 Since 2 radians corresponds to one complete revolution 360 = 2 rad or 180 = rad. Which gives us the following conversions: Degree Measure Example 3 – Converting from Degrees to Radians a. Multiply by / 180. b. Multiply by / 180. c. Multiply by / 180. Applications The radian measure formula, = s / r, can be used to measure arc length along a circle. Example 5 – Finding Arc Length A circle has a radius of 4 inches. Find the length of the arc intercepted by a central angle of 240. Example 5 – Solution To use the formula s = r, first convert 240 to radian measure. Example 5 – Solution cont’d Since the radius, r = 4 inches s = r Applications A sector of a circle is the region bounded by two radii of the circle and their intercepted arc. Area of the sector 1 퐴 = 푟2휃 (where 휃 is in radians) 2.
Load more

Recommended publications
  • Calculating Growing Degree Days by Jim Nugent District Horticulturist Michigan State University
    Calculating Growing Degree Days By Jim Nugent District Horticulturist Michigan State University Are you calculating degree day accumulations and finding your values don't match the values being reported by MSU or your neighbor's electronic data collection unit? There is a logical reason! Three different methods are used to calculate degree days; i.e., 1) Averaging Method; 2) Baskerville-Emin (BE) Method; and 3) Electronic Real-time Data Collection. All methods attempt to calculate the heat accumulation above a minimum threshold temperature, often referred to the base temperature. Once both the daily maximum and minimum temperatures get above the minimum threshold temperature, (i.e., base temperature of 42degrees, 50degrees or whatever other base temperature of interest) then all methods are fairly comparable. However, differences do occur and these are accentuated in an exceptionally long period of cool spring temperatures, such as we experienced this year. Let me briefly explain: 1. Averaging Method: Easy to calculate Degree Days(DD) = Average daily temp. - Base Temp. = (max. + min.) / 2 - Base temp. If answer is negative, assume 0. Example: Calculate DD Base 50 given 65 degrees max. and 40 degrees min. Avg. = (65 + 40) / 2 = 52.5 degrees DD base 50 = 52.5 - 50 = 2.5 degrees. But look what happens given a maximum of 60 degrees and a minimum of 35 degrees: Avg. = (60 + 35) / 2 = 47.5 DD base 50 = 47.5 - 50 = -2.5 = 0 degrees. The maximum temperature was higher than the base of 50° , but no degree days were accumulated. A grower called about the first of June reporting only about 40% of the DD50 that we have recorded.
    [Show full text]
  • Angles ANGLE Topics • Coterminal Angles • Defintion of an Angle
    Angles ANGLE Topics • Coterminal Angles • Defintion of an angle • Decimal degrees to degrees, minutes, seconds by hand using the TI-82 or TI-83 Plus • Degrees, seconds, minutes changed to decimal degree by hand using the TI-82 or TI-83 Plus • Standard position of an angle • Positive and Negative angles ___________________________________________________________________________ Definition: Angle An angle is created when a half-ray (the initial side of the angle) is drawn out of a single point (the vertex of the angle) and the ray is rotated around the point to another location (becoming the terminal side of the angle). An angle is created when a half-ray (initial side of angle) A: vertex point of angle is drawn out of a single point (vertex) AB: Initial side of angle. and the ray is rotated around the point to AC: Terminal side of angle another location (becoming the terminal side of the angle). Hence angle A is created (also called angle BAC) STANDARD POSITION An angle is in "standard position" when the vertex is at the origin and the initial side of the angle is along the positive x-axis. Recall: polynomials in algebra have a standard form (all the terms have to be listed with the term having the highest exponent first). In trigonometry, there is a standard position for angles. In this way, we are all talking about the same thing and are not trying to guess if your math solution and my math solution are the same. Not standard position. Not standard position. This IS standard position. Initial side not along Initial side along negative Initial side IS along the positive x-axis.
    [Show full text]
  • Guide for the Use of the International System of Units (SI)
    Guide for the Use of the International System of Units (SI) m kg s cd SI mol K A NIST Special Publication 811 2008 Edition Ambler Thompson and Barry N. Taylor NIST Special Publication 811 2008 Edition Guide for the Use of the International System of Units (SI) Ambler Thompson Technology Services and Barry N. Taylor Physics Laboratory National Institute of Standards and Technology Gaithersburg, MD 20899 (Supersedes NIST Special Publication 811, 1995 Edition, April 1995) March 2008 U.S. Department of Commerce Carlos M. Gutierrez, Secretary National Institute of Standards and Technology James M. Turner, Acting Director National Institute of Standards and Technology Special Publication 811, 2008 Edition (Supersedes NIST Special Publication 811, April 1995 Edition) Natl. Inst. Stand. Technol. Spec. Publ. 811, 2008 Ed., 85 pages (March 2008; 2nd printing November 2008) CODEN: NSPUE3 Note on 2nd printing: This 2nd printing dated November 2008 of NIST SP811 corrects a number of minor typographical errors present in the 1st printing dated March 2008. Guide for the Use of the International System of Units (SI) Preface The International System of Units, universally abbreviated SI (from the French Le Système International d’Unités), is the modern metric system of measurement. Long the dominant measurement system used in science, the SI is becoming the dominant measurement system used in international commerce. The Omnibus Trade and Competitiveness Act of August 1988 [Public Law (PL) 100-418] changed the name of the National Bureau of Standards (NBS) to the National Institute of Standards and Technology (NIST) and gave to NIST the added task of helping U.S.
    [Show full text]
  • Applications of Geometry and Trigonometry
    P1: FXS/ABE P2: FXS 9780521740517c14.xml CUAU031-EVANS September 6, 2008 13:36 CHAPTER 14 MODULE 2 Applications of geometry and trigonometry How do we apply trigonometric techniques to problems involving angles of depression and elevation? How do we apply trigonometric techniques to problems involving bearings? How do we apply trigonometric techniques to three-dimensional problems? How do we draw and interpret contour maps? How do we draw and interpret scale drawings? 14.1 Angles of elevation and depression, bearings, and triangulation Angles of elevation and depression The angle of elevation is the angle The angle of depression is the angle between the horizontal and a between the horizontal and a direction below direction above the horizontal. the horizontal. eye level line of sight angle of depression line of sight eye level cliff angle of elevation SAMPLEboat Cambridge University Press • Uncorrected Sample pages • 978-0-521-61328-6 • 2008 © Jones, Evans, Lipson TI-Nspire & Casio ClassPad material in collaboration with Brown410 and McMenamin P1: FXS/ABE P2: FXS 9780521740517c14.xml CUAU031-EVANS September 6, 2008 13:36 Chapter 14 — Applications of geometry and trigonometry 411 Bearings The three-figure bearing (or compass bearing) is the direction measured clockwise from north. The bearing of A from O is 030◦. The bearing of C from O is 210◦. The bearing of B from O is 120◦. The bearing of D from O is 330◦. N D N A 30° 330° E 120° E W O 210° W O B C S S Example 1 Angle of depression The pilot of a helicopter flying at 400 m observes a small boat at an angle of depression of 1.2◦.
    [Show full text]
  • 1. What Is the Radian Measure of an Angle Whose Degree Measure Is 72◦ 180◦ 72◦ = Πradians Xradians Solving for X 72Π X = Radians 180 2Π X = Radians 5 Answer: B
    1. What is the radian measure of an angle whose degree measure is 72◦ 180◦ 72◦ = πradians xradians Solving for x 72π x = radians 180 2π x = radians 5 Answer: B 2. What is the length of AC? Using Pythagorean Theorem: 162 + b2 = 202 256 + b2 = 400 b2 = 144 b = 12 Answer: E 3. one solution to z2 + 64 = 0 is z2 + 64 = 0 z2 = −64 p p z2 = −64 Since there is a negative under the radical, we get imaginary roots. Thus z = −8i or z = +8i Answer: A 4. Simplifying: p 36x10y12 − 36y12 = p36y12 (x10 − 1) p = 36y12p(x10 − 1) p = 6y6 x10 − 1 Answer: C 1 5. Simplifying: 1 1 1 1 1 −3 9 6 3 −3 9 6 27a b c = 27 3 a 3 b 3 c 3 = 3a−1b3c2 3b3c2 = a Answer: C 6. Solving for x: p 8 + x + 14 = 12 p x + 14 = 12 − 8 p x + 14 = 4 p 2 x + 14 = 42 x + 14 = 16 x = 16 − 14 x = 2 Answer: C 7. Simplify x2 − 9 (x + 1)2 2x − 6 × ÷ x2 − 1 (2x + 3)(x + 3) 1 − x Rewrite as a multiplication. x2 − 9 (x + 1)2 1 − x × x2 − 1 (2x + 3)(x + 3) 2x − 6 Simplify each polynomial (x − 3)(x + 3) (x + 1)(x + 1) 1 − x × (x − 1)(x + 1) (2x + 3)(x + 3) 2(x − 3) Canceling like terms (x + 1) − 2(2x + 3) Answer: C 2 8. Simplifying: 1 11 x−5 11 + 2 2 + 2 x−5 (x−5) = (x−5) (x−5) x + 1 x + 1 x−5+11 2 = (x−5) x + 1 x+6 2 = (x−5) x + 1 x + 6 = (x − 5)2(x + 1) Answer: B 9.
    [Show full text]
  • 4.1 – Radian and Degree Measure
    4.1 { Radian and Degree Measure Accelerated Pre-Calculus Mr. Niedert Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 1 / 27 2 Radian Measure 3 Degree Measure 4 Applications 4.1 { Radian and Degree Measure 1 Angles Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 3 Degree Measure 4 Applications 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 4 Applications 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure 3 Degree Measure Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 4.1 { Radian and Degree Measure 1 Angles 2 Radian Measure 3 Degree Measure 4 Applications Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 2 / 27 The starting position of the ray is the initial side of the angle. The position after the rotation is the terminal side of the angle. The vertex of the angle is the endpoint of the ray. Angles An angle is determine by rotating a ray about it endpoint. Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 3 / 27 The position after the rotation is the terminal side of the angle. The vertex of the angle is the endpoint of the ray. Angles An angle is determine by rotating a ray about it endpoint. The starting position of the ray is the initial side of the angle. Accelerated Pre-Calculus 4.1 { Radian and Degree Measure Mr. Niedert 3 / 27 The vertex of the angle is the endpoint of the ray.
    [Show full text]
  • Relationships of the SI Derived Units with Special Names and Symbols and the SI Base Units
    Relationships of the SI derived units with special names and symbols and the SI base units Derived units SI BASE UNITS without special SI DERIVED UNITS WITH SPECIAL NAMES AND SYMBOLS names Solid lines indicate multiplication, broken lines indicate division kilogram kg newton (kg·m/s2) pascal (N/m2) gray (J/kg) sievert (J/kg) 3 N Pa Gy Sv MASS m FORCE PRESSURE, ABSORBED DOSE VOLUME STRESS DOSE EQUIVALENT meter m 2 m joule (N·m) watt (J/s) becquerel (1/s) hertz (1/s) LENGTH J W Bq Hz AREA ENERGY, WORK, POWER, ACTIVITY FREQUENCY second QUANTITY OF HEAT HEAT FLOW RATE (OF A RADIONUCLIDE) s m/s TIME VELOCITY katal (mol/s) weber (V·s) henry (Wb/A) tesla (Wb/m2) kat Wb H T 2 mole m/s CATALYTIC MAGNETIC INDUCTANCE MAGNETIC mol ACTIVITY FLUX FLUX DENSITY ACCELERATION AMOUNT OF SUBSTANCE coulomb (A·s) volt (W/A) C V ampere A ELECTRIC POTENTIAL, CHARGE ELECTROMOTIVE ELECTRIC CURRENT FORCE degree (K) farad (C/V) ohm (V/A) siemens (1/W) kelvin Celsius °C F W S K CELSIUS CAPACITANCE RESISTANCE CONDUCTANCE THERMODYNAMIC TEMPERATURE TEMPERATURE t/°C = T /K – 273.15 candela 2 steradian radian cd lux (lm/m ) lumen (cd·sr) 2 2 (m/m = 1) lx lm sr (m /m = 1) rad LUMINOUS INTENSITY ILLUMINANCE LUMINOUS SOLID ANGLE PLANE ANGLE FLUX The diagram above shows graphically how the 22 SI derived units with special names and symbols are related to the seven SI base units. In the first column, the symbols of the SI base units are shown in rectangles, with the name of the unit shown toward the upper left of the rectangle and the name of the associated base quantity shown in italic type below the rectangle.
    [Show full text]
  • Draft 9Th Edition of the SI Brochure
    —————————————————————————— Bureau International des Poids et Mesures The International System of Units (SI) 9th edition 2019 —————————————————— 2 ▪ Draft of the ninth SI Brochure, 5 February 2018 The BIPM and the Metre Convention The International Bureau of Weights and Measures (BIPM) was set up by the Metre As of 20 May 2019, fifty Convention signed in Paris on 20 May 1875 by seventeen States during the final session of nine States were Members of this Convention: the diplomatic Conference of the Metre. This Convention was amended in 1921. Argentina, Australia, 2 Austria, Belgium, Brazil, The BIPM has its headquarters near Paris, in the grounds (43 520 m ) of the Pavillon de Bulgaria, Canada, Chile, Breteuil (Parc de Saint-Cloud) placed at its disposal by the French Government; its upkeep China, Colombia, Croatia, is financed jointly by the Member States of the Metre Convention. Czech Republic, Denmark, Egypt, Finland, The task of the BIPM is to ensure worldwide unification of measurements; its function is France, Germany, Greece, Hungary, India, Indonesia, thus to: Iran (Islamic Rep. of), • establish fundamental standards and scales for the measurement of the principal physical Iraq, Ireland, Israel, Italy, Japan, Kazakhstan, quantities and maintain the international prototypes; Kenya, Korea (Republic • carry out comparisons of national and international standards; of), Lithuania, Malaysia, • ensure the coordination of corresponding measurement techniques; Mexico, Montenegro, Netherlands, New • carry out and coordinate measurements of the fundamental physical constants relevant Zealand, Norway, to these activities. Pakistan, Poland, Portugal, Romania, The BIPM operates under the exclusive supervision of the International Committee for Russian Federation, Saudi Weights and Measures (CIPM) which itself comes under the authority of the General Arabia, Serbia, Singapore, Slovakia, Slovenia, South Conference on Weights and Measures (CGPM) and reports to it on the work accomplished Africa, Spain, Sweden, by the BIPM.
    [Show full text]
  • The International System of Units (SI)
    NAT'L INST. OF STAND & TECH NIST National Institute of Standards and Technology Technology Administration, U.S. Department of Commerce NIST Special Publication 330 2001 Edition The International System of Units (SI) 4. Barry N. Taylor, Editor r A o o L57 330 2oOI rhe National Institute of Standards and Technology was established in 1988 by Congress to "assist industry in the development of technology . needed to improve product quality, to modernize manufacturing processes, to ensure product reliability . and to facilitate rapid commercialization ... of products based on new scientific discoveries." NIST, originally founded as the National Bureau of Standards in 1901, works to strengthen U.S. industry's competitiveness; advance science and engineering; and improve public health, safety, and the environment. One of the agency's basic functions is to develop, maintain, and retain custody of the national standards of measurement, and provide the means and methods for comparing standards used in science, engineering, manufacturing, commerce, industry, and education with the standards adopted or recognized by the Federal Government. As an agency of the U.S. Commerce Department's Technology Administration, NIST conducts basic and applied research in the physical sciences and engineering, and develops measurement techniques, test methods, standards, and related services. The Institute does generic and precompetitive work on new and advanced technologies. NIST's research facilities are located at Gaithersburg, MD 20899, and at Boulder, CO 80303.
    [Show full text]
  • Angles Are Inherently Neither Length Ratios Nor Dimensionless
    Angles are inherently neither length ratios nor dimensionless Paul Quinceya, Peter J Mohrb and William D Phillipsb a National Physical Laboratory, Hampton Road, Teddington, TW11 0LW, United Kingdom b National Institute of Standards and Technology, Gaithersburg, MD 20899, USA Accepted for publication by Metrologia, 7 June 2019 Abstract The status of angles within The International System of Units (SI) has long been a source of controversy and confusion. We address one specific but crucial issue, putting the case that the idea of angles necessarily being length ratios, and hence dimensionless, is not valid. By making a clear distinction between the definition of a quantity and the process of making a measurement of that quantity, we show that the usual arguments for angles being length ratios are problematic. An appreciation of this point should clear away a major obstacle preventing a more proper treatment of the angle problem. Introduction One way to point out the odd status of angles within the SI is as follows: angle is measurable with a scale, on a protractor, in analogy to the way length is measureable with a ruler. It can therefore have units that are chosen by the user. This simple point is reinforced by the fact that multiple units for angle are used in practice. Angle measurements often use the degree, while the radian, which is used in mathematics and theoretical physics, is the SI unit. Other units, such as the grad, are used in specialised areas. And yet angle is treated as being dimensionless in the SI, a status usually applied only to quantities that are simply counted, like the number of molecules in a container, or quantities that are clearly a ratio of two values of the same quantity, such as refractive index.
    [Show full text]
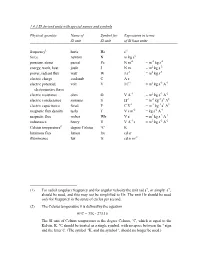
  • 1.4.3 SI Derived Units with Special Names and Symbols
    1.4.3 SI derived units with special names and symbols Physical quantity Name of Symbol for Expression in terms SI unit SI unit of SI base units frequency1 hertz Hz s-1 force newton N m kg s-2 pressure, stress pascal Pa N m-2 = m-1 kg s-2 energy, work, heat joule J N m = m2 kg s-2 power, radiant flux watt W J s-1 = m2 kg s-3 electric charge coulomb C A s electric potential, volt V J C-1 = m2 kg s-3 A-1 electromotive force electric resistance ohm Ω V A-1 = m2 kg s-3 A-2 electric conductance siemens S Ω-1 = m-2 kg-1 s3 A2 electric capacitance farad F C V-1 = m-2 kg-1 s4 A2 magnetic flux density tesla T V s m-2 = kg s-2 A-1 magnetic flux weber Wb V s = m2 kg s-2 A-1 inductance henry H V A-1 s = m2 kg s-2 A-2 Celsius temperature2 degree Celsius °C K luminous flux lumen lm cd sr illuminance lux lx cd sr m-2 (1) For radial (angular) frequency and for angular velocity the unit rad s-1, or simply s-1, should be used, and this may not be simplified to Hz. The unit Hz should be used only for frequency in the sense of cycles per second. (2) The Celsius temperature θ is defined by the equation θ/°C = T/K - 273.15 The SI unit of Celsius temperature is the degree Celsius, °C, which is equal to the Kelvin, K.
    [Show full text]
  • Angles and Degree Measures an Angle May Be Generated by Rotating One of Two Rays That Share a Fixed Endpoint, a Vertex
    Angles and Degree Measures An angle may be generated by rotating one of two rays that share a fixed endpoint, a vertex. Terminal Side Vertex Initial Side The measure of an angle provides us with information concerning the direction of the rotation and the amount of the rotation necessary to move from the initial side of the angle to the terminal side. Positive Angle Negative angle if the rotation is in a counterclockwise direction if the rotation is in a clockwise direction Standard Position Terminal Side 45 Vertex Initial Side 45 Quadrantal Angle is an angle with a terminal side coincided with one of the axis. 0 or -360 Quadrantal Angle is an angle with a terminal side coincided with one of the axis. 90 or -270 Quadrant I Quadrantal Angle is an angle with a terminal side coincided with one of the axis. Quadrant II 0 180 or -180 Quadrantal Angle is an angle with a terminal side coincided with one of the axis. Quadrant III 270 or -90 Quadrantal Angle is an angle with a terminal side coincided with one of the axis. 360 or 0 Quadrant VI Degree measurement came from the Babylonian culture. They used a numerical system based on 60 rather than 10. They assumed that the measure of each angle of an equilateral triangle is 60 The 1/60 of the measure of each angle of an equilateral triangle is 1degree The 1/60 of 1degree is 1’( minute). The 1/60 of 1’ is 1”(second) Example 1 GEOGRAPHY Geographic locations are typically expressed in terms of latitude and longitude.
    [Show full text]