DOCSLIB.ORG

The Citadel Department of Electrical and Computer Engineering

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Citadel Department of Electrical and Computer Engineering THE CITADEL DEPARTMENT OF ELECTRICAL AND COMPUTER ENGINEERING ELEC105-01 Engineering Fundamnetals II Spring 2003 |1| (20 points) A table of 24 data points is given below. Complete the frequency distribution table and plot the histogram on the graph provided. 92 71 89 91 53 93 98 76 96 94 68 91 88 87 93 78 85 98 78 70 87 88 89 95 Classes Frequency FREQUENCY 10 48 - 54 1 8 55 - 61 0 62 - 68 1 6 69 - 75 2 4 76 - 82 3 2 83 - 89 7 0 90 - 96 8 48 55 62 69 76 83 90 97 104 97 - 103 2 CLASSES Frequency Distribution |2| (20 points) The 10 data points listed under x in the table below are a sample, selected at random, of the highest daily temperatures recorded in Philadelphia. Complete the table and find the mean of the data m and its standard deviation s . x x ! m (x ! m)2 67 11.9 141.61 2 ! 53.1 2819.61 93 37.9 1436.41 97 41.9 1755.61 23 ! 32.1 1030.41 83 27.9 778.41 35 ! 20.1 404.01 38 ! 17.1 292.41 33 ! 22.1 488.41 80 24.9 620.01 m = ______55.1_________________________ s = _______32.94________________________ j xi 551 m ' ' n 10 2 j (xi ! m) 9766.9 s 2 ' ' (n ! 1) 9 s ' 1085.21 ' 32.94 |3| (10 points) Write the equation for the mean µ of a population. j xi µ ' n Write the equation for the standard deviation F of a population. 2 1/2 j (xi ! µ) F ' n The mean is a meaure of ___central tendency__________________ The standard deviation is a measure of ___variation______________ |4| (20 points) A manufacturer of electronic components produces a run of 100,000 molded carbon resistors. The mean of the resistors in the run is 1 kS and the standard deviation is 40S . The resistor values in the run follow a normal distribution. (a) Find the expected number of resistors that have values between 950S and 1050S . (b) Find the expected number of resistors that have values between 990S and 1010S . Given: N = 100,000 resistors µ = 1 kS F = 40 S normal distribution (a) Find: n = ? such that 950 S # R # 1050 S Solution: 950 ! 1000 z ' ' ! 1.25 1 40 1050 ! 1000 z ' ' 1.25 2 40 From the table of normal distribution, P(0 # z # 1.25) ' 0.3944 P(! 1.25 # z # 1.25) ' 2 (0.3944) ' 0.7888 n ' P×N ' 0.7888 (100,000) Answer: n = 78,880 resistors (b) Find: n = ? such that 990 S # R # 1010 S Solution: 990 ! 1000 z ' ' ! 0.25 1 40 1010 ! 1000 z ' ' 0.25 2 40 From the table of normal distribution, P(0 # z # 0.25) ' 0.0987 P(! 0.25 # z # 0.25) ' 2 (0.0987) ' 0.1974 n ' P×N ' 0.1974 (100,000) Answer: n = 19,740 resistors |5| (10 points) List the two parameters that completely describe a normal distribution. _______mean, _µ_____________________ _______standard deviation, F_________ List two of the three properties of a normal distribution. _______symmetrical about the mean______________ _______extends to infinity in both directions______ _______total area = 1____________________________ |6| (20 points) A normal distribution has a mean of 26 and a standard deviation of 8. (a) Determine the probability of values between 26 and 36. (b) Determine the probability of values greater than 40. (c ) Determine the probability of values less than 22 . Given: µ = 26 F = 8 (a) Find: P(x) = ? Such that 26 # x # 36 Solution: 26 ! 26 z ' ' 0 1 8 36 ! 26 z ' ' 1.25 2 8 From the table of normal distribution, P(0 # z # 1.25) ' 0.3944 Answer: P(x) = 0.3944 (b) Find: P(x) = ? such that x $ 36 Solution: 40 ! 26 z ' ' 1.75 8 From the table of normal distribution, P(0 # z # 1.75) ' 0.4599 P(z $ 1.75) ' 0.5 ! 0.4599 Answer: P(x) = 0.0401 (c ) Find: P(x) = ? such that x # 22 Solution: 22 ! 26 z ' ' ! 0.5 8 From the table of normal distribution, P(0 # z # 0.5) ' 0.1915 P(z # ! 0.5) ' 0.5 ! 0.1915 Answer: P(x) = 0.3085.
Load more

Recommended publications
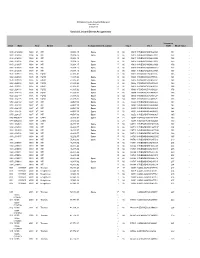
  • Vehicle List and Driver Assignments
    Effingham County Board of Education Vehicle List 6/30/2013 Vehicle List and Driver Assignments Insurance Veh# Make Year Model Cost Assigned Driver/Location Tag # Vin # Car# Book Value 940 L0163292 1994 94 INT 39,994.15 Spare BB 66 15915 1HVBBACNXSH623821 151 - 941 L016393 1994 94 INT 39,994.15 Spare BB 66 15916 1HVBBACN1SH623822 153 - 942 L016394 1994 94 INT 39,994.15 BB 66 15917 1HVBBACN3SH623823 152 - 944 L016396 1994 94 INT 39,994.15 Spare BB 66 15918 1HVBBACN7SH623825 155 - 945 L016397 1994 94 INT 39,994.15 Spare BB 66 15919 1HVBBACN9SH623826 156 - 946 L016398 1994 94 INT 39,994.15 Spare BB 66 15920 1HVBBACNOSH623827 158 - 947 L016399 1994 94 INT 39,994.15 Spare BB 66 15921 1HVBBACN2SH623828 157 - 951 L020327 1995 95 FORD 41,995.62 BB 66 15923 1FDXB80C1SVA75535 165 - 952 L020328 1995 95 FORD 41,995.62 Spare BB 66 15924 1FDXB80C3SVA75536 164 - 953 L020329 1995 95 FORD 41,995.62 Spare BB 66 15925 1FDXB80C5SVA75537 168 - 954 L020330 1995 95 FORD 41,995.62 Spare BB 66 15926 1FDXB80CXSVA79843 169 - 956 L020332 1995 95 FORD 41,995.62 Spare BB 66 15928 1FDXB80C8SVA76228 166 - 962 L024118 1996 96 FORD 41,995.62 Spare BB 66 15963 1FDXB80C5VVA03628 176 - 963 L024119 1996 96 FORD 41,995.62 Spare BB 66 15964 1FDXB80C7VVA03629 175 - 964 L024117 1996 96 FORD 41,995.62 Spare BB 54 15965 1FDXB80C3VVA03627 177 - 965 L024116 1996 96 FORD 41,995.62 Spare BB 54 15966 1FDXB80C1VVA03626 178 - 970 L028102 1997 97 INT 44,597.30 Spare BB 66 16029 1HVBBABN8VH496962 181 - 971 L028103 1997 97 INT 44,597.30 Spare BB 66 16048 1HVBBABNXVH496963 182 - 973 L028105
    [Show full text]
  • UNIVERSITY of CALIFORNIA RIVERSIDE Modeling
    UNIVERSITY OF CALIFORNIA RIVERSIDE Modeling, Characterization and Simulation of On-Chip Power Delivery Networks and Temperature Profile on Multi-Core Microprocessors A Dissertation submitted in partial satisfaction of the requirements for the degree of Doctor of Philosophy in Electrical Engineering by Duo Li December 2010 Dissertation Committee: Dr. Sheldon X.-D. Tan, Chairperson Dr. Yingbo Hua Dr. Frank Vahid Copyright by Duo Li 2010 The Dissertation of Duo Li is approved: Committee Chairperson University of California, Riverside ACKNOWLEDGMENT There are many thanks to many people who made this dissertation possible. First of all, I would like to thank my Ph.D. advisor Dr. Sheldon Tan for the continuous support to my Ph.D. study and research work. Thank him for guiding me on my research road and providing me the great lab research environment. I could not have finished my dissertation successfully without his encouragement, sound advice, good teaching and lots of good ideas. Besides my advisor, I would like to thank the rest of my Ph.D. dissertation committee members Dr. Yingbo Hua and Dr. Frank Vahid, for their encouragement, comments and questions. I would like to thank all my labmates for their support and encouragement. I could not have had the better understanding on my research without the frequent discussions with them. I would like to thank my parents Daping Li and Yuqin Cong for giving birth to me, rasing me, teaching me, supporting me and loving me all the time. Last but not the least, I would like to thank my lovely wife Shan Shan. Thanks for being with me together during my Ph.D.
    [Show full text]
  • A File in the Online Version of the Kouroo Contexture (Approximately
    SETTING THE SCENE FOR THOREAU’S POEM: YET AGAIN WE ATTEMPT TO LIVE AS ADAM 11th Century 1010s 1020s 1030s 1040s 1050s 1060s 1070s 1080s 1090s 12th Century 1110s 1120s 1130s 1140s 1150s 1160s 1170s 1180s 1190s 13th Century 1210s 1220s 1230s 1240s 1250s 1260s 1270s 1280s 1290s 14th Century 1310s 1320s 1330s 1340s 1350s 1360s 1370s 1380s 1390s 15th Century 1410s 1420s 1430s 1440s 1450s 1460s 1470s 1480s 1490s 16th Century 1510s 1520s 1530s 1540s 1550s 1560s 1570s 1580s 1590s 17th Century 1610s 1620s 1630s 1640s 1650s 1660s 1670s 1680s 1690s 18th Century 1710s 1720s 1730s 1740s 1750s 1760s 1770s 1780s 1790s 19th Century 1810s Alas! how little does the memory of these human inhabitants enhance the beauty of the landscape! Again, perhaps, Nature will try, with me for a first settler, and my house raised last spring to be the oldest in the hamlet. To be a Christian is to be Christ- like. VAUDÈS OF LYON 1600 William Gilbert, court physician to Queen Elizabeth, described the earth’s magnetism in DE MAGNETE. Robert Cawdrey’s A TREASURIE OR STORE-HOUSE OF SIMILES. Lord Mountjoy assumed control of Crown forces, garrisoned Ireland, and destroyed food stocks. O’Neill asked for help from Spain. HDT WHAT? INDEX 1600 1600 In about this year Robert Dudley, being interested in stories he had heard about the bottomlessness of Eldon Hole in Derbyshire, thought to test the matter. George Bradley, a serf, was lowered on the end of a lengthy rope. Dudley’s little experiment with another man’s existence did not result in the establishment of the fact that holes in the ground indeed did have bottoms; instead it became itself a source of legend as spinners would elaborate a just-so story according to which serf George was raving mad when hauled back to the surface, with hair turned white, and a few days later would succumb to the shock of it all.
    [Show full text]
  • ROTARY INTERNATIONAL DISTRICT 5450 FILING 990S - Basics March, 2021
    ROTARY INTERNATIONAL DISTRICT 5450 FILING 990s - Basics March, 2021 Every Rotary Club 501(c)(4) and every Rotary Foundation 501(c)(3) is required to file a tax return and mail to the IRS every year. A nonprofit, tax-exempt organization does not exempt an organization from the requirement to file. What form to file (depends on gross income and assets of your club): Gross income/Total assets File Form Gross income $50,000 or less 990- N (e- postcard) Gross income >$50,000 <$200,000 990 EZ Gross income > $200,000 or $500,000 total assets 990 WHEN: Due date of return: 15th day of the 5th month after year end November 15th for club and foundation with a June 30th fiscal year end. WHERE: If paper filing: Department of the Treasury Internal Revenue Service Center Ogden, UT 84201-0027 EXTENSION: Available automatic six month extension, use Form 8868 WHEN: File on or before the date the original return is due. WHERE: If paper filing: Department of the Treasury Internal Revenue Service Center Ogden, UT 84201-0045 PENALTIES FOR NONFILING: A penalty of $20 a day (IRC Section 6652(c)(1)(A)) can be charged if a return is filed late. Exceptions and limitations apply. LOSS OF TAX EXEMPT STATUS: If an organization does not file an annual return for 3 consecutive years, its tax exempt status is automatically revoked. The organization which has lost tax-exempt status may need to file tax returns as taxable entity and pay taxes. Has your club lost its tax exempt status? Go to: www.irs.gov Then to: Tax Exempt Organization Search (formerly Select Check) to check club status.
    [Show full text]
  • Electric Actuators Vsi-1000 Series
    ELECTRIC ACTUATORS TM VSI-1000 SERIES DESCRIPTION VSI-1000 Series Electric Actuators are used on Kele KBV Series butterfly valves to provide two-position (with or without battery backup) or proportional control in a NEMA 4X housing. The VSI-1000 Series comes standard on 8" and larger non-spring return assemblies and on 5" and larger two- position spring return assemblies. They can be ordered on smaller valve assemblies as an option. Standard fea- tures include 2 SPDT fully adjustable auxiliary switches KBV-2-6-E2SO (two-position only), manual override crank, and an inter- assembly includes nal heater to prevent condensation in outdoor installa- VSI-BB1020 actuator tions. SPECIFICATIONS FEATURES Power 120 VAC standard •Lightweight, compact design Models 1005 to 1020 12/24 VDC optional • Two-position or modulating control Models 1005 to 1040 24 VAC optional • Two-position battery-backed models Torque range 347-17,359 in-lb • NEMA 4X watertight, corrosion-resistant housing Motor 120 VAC, 1 phase, 60 Hz; • Integral position indicator enclosed, non-ventilated, high • Space heater standard starting torque, reversible induc- • Two 1/2" conduit connections tion, Class E insulation • Detachable manual override crank Thermal overload Auto reset, embedded • Terminal strip wiring Travel limit switches Cam operated, adjustable SPDT • Worm gear drive, no electro-mechanical brake for open/close stop required • Mounting orientation in any direction Position indicator High-visibility graduated dial • 4-20 mA or 500Ω optional feedback signal Conduit connections
    [Show full text]
  • Download Running Start's 990S
    OMB No. 1545-0047 Form 990 Return of Organization Exempt From Income Tax 2017 Under section 501(c), 527, or 4947(a)(1) of the Internal Revenue Code (except private foundations) G Do not enter social security numbers on this form as it may be made public. Open to Public Department of the Treasury Internal Revenue Service G Go to www.irs.gov/Form990 for instructions and the latest information. Inspection A For the 2017 calendar year, or tax year beginning , 2017, and ending , B Check if applicable: C D Employer identification number Address change Running Start 20-8666097 Name change 1310 L Street, NW #820 E Telephone number Initial return Washington, 20005, 2022233895 Final return/terminated Amended return G Gross receipts $ 1,084,331. Application pending F Name and address of principal officer: Susannah Wellford H(a) Is this a group return for subordinates? Yes X No H(b) Are all subordinates included? Yes No Same As C Above If 'No,' attach a list. (see instructions) I Tax-exempt status X 501(c)(3) 501(c) ()H (insert no.) 4947(a)(1) or 527 J Website: G runningstart.org H(c) Group exemption number G K Form of organization: X Corporation Trust Association OtherG L Year of formation: 2007 M State of legal domicile: Part I Summary 1 Briefly describe the organization's mission or most significant activities:Training young women to run for political office on a nonpartisan basis. 2 Check this box G if the organization discontinued its operations or disposed of more than 25% of its net assets.
    [Show full text]
  • X"997 13 0 a 14 Occupancy, Rent, Utilities, and Maintenance
    Short Form OMB No 1545-1150 Fwm 990-EZ, Return of Organization Exempt From Income Tax Under section 501(c), 527, or 4947(a)(1) of the Internal Revenue Code (except private foundations) 41115- 0 0 form as it may ► Do not enter social seaaity numbers on this be made public. Information about Form 990-EZ and its instructions is at www.bs.gov/lonn9®0. ► ia A For the 2015 calendar year, or tax year beginning October 1 , 2015, and ending September 30 .20 16 g check it appp e C Name of organization D Employer Identification number 0 Address diang• Optimist tntemationa135 Dakotas Manitoba Minnesota District 41-6053928 q Name change Number and street (or P.O. box, if mail is not delivered to street address) Room/surte E Telephone number inmainiturn q F ^ 475 Marley Avenue 204 453-7524 wm q Gly w town, state w province, country, and ZIP w foreign postal code F Group Exemption Amended Appsaeanperilina lonnima. L QY8 Number ► 1334 q Other (specify) G Accounting Method: 0 Cash Accrual ► H Check ► 0 if the organization is not Website: ► www.optitnist-dmm.org required to attach Schedule B J Tax-en pt slates (check only one) - q 501 (c)(3 ) q 501 c 4 t insert no.) q 4947(a)(1 ) or [1527 (Form 990, 990-E. or 990-PF). K Form of organization: q Corporation q Trust 2 Association q Other L Add lines 5b, 6c, and 7b to line 9 to determine gross receipts. If gross receipts are $200,000 or more, or if total assets (Part 11, column (B) below) are $500,000 or more, file Form 990 instead of Form 990-EZ .
    [Show full text]
  • 3.2 Precipitation Or Dry-Wet Reconstructions
    Climate change in China during the past 2000 years: An overview Ge Quansheng , Zheng Jingyun Institute of Geographic Sciences and Natural Resources Research, Chinese Academy of Sciences, Beijing 100101, China Email: [email protected] Outline 1 Introduction 2 Historical Documents as Proxy 3 Reconstructions and Analyses 4 Summary and Prospects 1. Introduction: E Asia2K Climate System Socio-economic System •typical East Asian •dense population and rapid monsoon climate economic development • significant seasonal and • be susceptible to global inter-annual and inter- warming and extreme decadal variability climate events Climate change study in the past 2ka in East Asian is both beneficial and advantageous. • various types of natural proxy • Plenty of historical documents Fig. Active regional working groups under as proxy the past 2ka theme (PAGES 2009) 2. Historical Documents as Proxy Type Period Amount Chinese classical 1,531 kinds, 137 BC~1470 AD documents 32,251 volumes More than 8,000 1471~1911 (The Ming Local gazettes books (部), 110, and Qing Dynasty) 000 volumes Memos to the About 120,000 1736~1911 emperor pieces Archives of the 1912~1949 20,000 volumes Republic of China More than 200 Private diaries 1550~ books (部) Chinese classical documents AD 833, North China plain: Extreme drought event was occurred, crops were shriveling, no yields, people were in hungry…. Fig. Example for Ancient Chinese writings Local gazettes The 28th year of the Daoguang reign (1848 AD), the 6th (lunar) month, strong wind and heavy rain, the Yangtze River overflowed; the 7th month, strong wind Fig. Gazettes of Yangzhou Prefecture and thunder storm, field published in 1874 AD and houses submerged.
    [Show full text]
  • Series 1000 Electric Actuators Series 1000 Electric Actuators Design Features
    SERIES 1000 ELECTRIC ACTUATORS SERIES 1000 ELECTRIC ACTUATORS DESIGN FEATURES Series 1000 On-Off Rotary Electric Actuator Basic Actuator: Torque Output Range: 347in-lb to 17,359in-lb Housing: NEMA 4X, watertight, corrosion-resistant, robust aluminum die cast Electric Motor: 10VAC, single phase, 60Hz totally enclosed, non-ventilated, high starting torque, reversible induction type, Class F insulation Thermal Overload Motor Protection: Auto reset thermal switch embedded in the motor winding - trips when the maximum winding temperature is exceded Position Limit Switches: x SPDT for Open and Close travel limit - easily adjustable, cam operated Position Indicator: Mechanical dome type with visiable red/yellow closed/open indicator Terminal Strip: Refer to wiring diagrams for details Conduit Entries: 1 x 1/” NPT for power and control wiring Power Gears: Alloy steel spur gears to final stage aluminum bronze worm sector gear Break: An electro-mechanical brake is NOT required. The worm gear drive prevents back driving and hunting Bearings: High quality alloy steel sleeve and ball bearings Manual Override: Handle Adjustable Mechanical Stops Ambient Temperature Range: -31°F to +150°F Certification and Approvals:CE, NEMA4, CSA, NRTL Internal Heater Optional Features • 0V AC/1/50-60Hz power • 1/4V DC 1005 through 100 • Torque Limit Switches for Close direction of travel • Feedback Potentiometer - 1000ohm • DeClutchable Handwheel Override SERIES 1000 ELECTRIC ACTUATORS ON-OFF SPECIFICATIONS Series 1000 On-Off Actuator Specifications Model 1005 1010 1020 1040 1060 1100 1150 1200 Output Torque(in-lb) 347 868 1736 347 508 8680 13,019 17,359 Output Torque(Nm) 39.3 98.06 196.13 39.7 588.4 980.66 1471 1961.3 Duty Cycle 75% 75% 50% 50% 50% 50% 50% 50% Travel Speed at 5 5 5 5 50 50 50 50 60Hz(Sec) Maximum Current .35/.18 .41/.
    [Show full text]
  • Tourism, the Economy, Population Growth, and Conservation in Galapagos
    Tourism, the Economy, Population Growth, and Conservation in Galapagos Bruce Epler CHARLES DARWIN FOUNDATION Puerto Ayora, Santa Cruz Island, Galapagos Islands, Ecuador Revised and Updated in September 2007 Tourism, the Economy, Population Growth, and Conservation in Galapagos ACKNOWLEDGMENTS The author is particularly indebted to Susana Cardenas who, in addition to providing general guidance and logistical support, oversaw the distribution and collection of surveys and data entry. Johanna Castañeda assisted in distributing surveys to tourists waiting to depart the airport on Baltra and data entry. Liz Llerena assisted in data entry and interviews with hotel owners on Santa Cruz. Jairo Alvarado circulated surveys in the airport on San Cristóbal. Paulina Buenaño, Carmen Nicolade, and Delsy Jaramillo assisted with surveys and interviews with hotels on Santa Cruz, San Cristóbal, and Isabela. Graham Watkins, Executive Director of the Charles Darwin Foundation (CDF), oversaw the study, provided numerous and relevant data files and studies, and submitted comments that improved the study. Johannah Barry, President of the Galapagos Conservancy, contributed data and insight into tourists’ and industry donations. Roslyn Cameron shared her knowledge about tour vessels, tourists, and fundraising. Craig MacFarland added information on the early years of the CDF, the development of the tourism industry, and ongoing and evolving issues and concerns. Oscar Aguirre, of the Galapagos Chamber of Tourism (CAPTURGAL), generously supplied summaries of survey information collected over several years. Edwin Naula, Head of the Galapagos National Park Service’s Tourism Unit, and Daniel Silva provided useful data compiled by the Park Service. Eliecer Cruz, of the World Wildlife Fund, provided insight into immigration, industry trends, and changes occurring in populated areas.
    [Show full text]
  • The Teen Project & Freehab 990S
    The Teen Project & Freehab 990s Please see the following 990 forms for both The Teen Project Inc. and Freehab Inc. herein. Freehab was dissolved and the assets merged under The Teen Project Inc. (the surviving organization) due to the long history, similar mission and supportive recurring donor base as is described herein. The Teen Project has five components: PAD Venice Drop in Center College Housing FREEHAB Life Transformation Center National Shelter Cell Service National Shelter Database OMB No. 1545-0047 Form 990 Return of Organization Exempt From Income Tax 2013 Under section 501(c), 527, or 4947(a)(1) of the Internal Revenue Code (except private foundations) G Do not enter Social Security numbers on this form as it may be made public. Open to Public Department of the Treasury G Internal Revenue Service Information about Form 990 and its instructions is at www.irs.gov/form990. Inspection A For the 2013 calendar year, or tax year beginning , 2013, and ending , B Check if applicable: C D Employer Identification Number Address change FREEHAB INC 46-1498077 E Name change 22431 B160 ANTONIO PKY #527 Telephone number X Initial return RANCHO SANTA MARGARITA, CA 92688 Terminated Amended return G Gross receipts $ 1,448,938. Application pending F Name and address of principal officer: H(a) Is this a group return for subordinates? Yes X No H(b) Are all subordinates included? Yes No If 'No,' attach a list. (see instructions) I Tax-exempt status X 501(c)(3) 501(c) ()H (insert no.) 4947(a)(1) or 527 G J Website: G N/A H(c) Group exemption number T G K Form of organization: X Corporation rust Association Other L Year of formation: 2013 M State of legal domicile: CA Part I Summary 1 Briefly describe the organization's mission or most significant activities: ORGANIZATION THAT PROVIDES "STREET TO EMPLOYMENT" SERVICES FOR THE HOMELESS, THE DISPOSED AND SOCIALLY IGNORED.
    [Show full text]
  • Legitimacy Through Literature: Political
    LEGITIMACY THROUGH LITERATURE: POLITICAL CULTURE IN EARLY- ELEVENTH-CENTURY ROUEN A Dissertation Presented to the Faculty of the Graduate School of Cornell University in Partial Fulfillment of the Requirements of the Degree of Doctor of Philosophy by Corinna MaxineCarol Matlis May 2017 © 2017 Corinna MaxineCarol Matlis LEGITIMACY THROUGH LITERATURE: POLITICAL CULTURE IN EARLY- ELEVENTH-CENTURY ROUEN Corinna Maxine Carol Matlis Cornell University 2017 This dissertation examines the interplay between early-eleventh-century Norman literature and the Norman ducal family’s project of establishing its legitimacy to rule. The dissertation considers Dudo of Saint Quentin’s arcane history of the Norman dukes, Warner of Rouen’s two esoteric satires, and two further anonymous satires produced in Rouen c. 996-1026 (the reign of Duke Richard II). These works constitute the secular Norman literature during this period. Although the texts’ audiences are unknown, it is clear that the ducal family, local clerics, and potentially nobility throughout the region and France were among the works’ addressees. Despite their obscurity to modern readers, these texts spoke to the interests of the highest echelons of Norman society. Throughout my dissertation, I show how these texts were understood in their own time and how they spoke to contemporary social and political issues. Common themes emerge throughout the texts, despite their different genres: most importantly, the ducal family’s strategic marriages, and the desire for the appearance of a cultured court in order to balance the Normans’ reputation of physical might. Reading these Rouennais texts together offers new views of Norman political culture that have not been available without a close look at this literature as a whole.
    [Show full text]