Dislocation and Strong Ground Motion Zoning Under Scenario Faults for Lifelines
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Landslide Zonation in Fasham Area of Tehran Province (Iran) Abstract Introduction
LANDSLIDE ZONATION IN FASHAM AREA OF TEHRAN PROVINCE (IRAN) Shadi Khoshdoni Farahani, Assoc.Prof.Dr.Md Nor Kamarudin, Dr. Mojgan Zarei Nejad Faculty of Geoinformation Science and Engineering, Universiti Teknologi Malaysia 81300 Skudai, Johor, Malaysia Email: [email protected] Faculty of Geoinformation Science and Engineering, Universiti Teknologi Malaysia 81300 Skudai, Johor , Malaysia Email: [email protected] GIS Center, Solvegatan 12, 223 62 Lund, Lund University, Sweden Email: [email protected] ABSTRACT Tehran province which encircles the capital of the Islamic Republic of Iran is highly momentous from the politico- socio-economic-cultural aspects. This significance has instigated the implementation of the geological, geographical and climatological studies in this state in a comprehensive and precise manner. Fasham district in the north eastern part of Tehran province which is a geologically and geographically area has been opted out in this research for semi- detailed studies. the case studied in this research is the landslide in Fasham area. Iran is one of the highly landslide prone countries due to its particular geological, topographical and climatological conditions. Heavy financial lost are reported each year due to the landslide occurrence. The transpiration of these landslides occasionally brings about other death tolls and financial lost originating from earthquakes. Some of the factors affecting this phenomenon are as follows: the alteration of the slope amplitude, geotechnical and litho logical circumstances, earthquake and trembling, tectonics motions, structural alterations, pluvial effects and snow thawing, the extermination of the vegetation, land utilization alteration. The zone under studied is prone to landslide due to various reasons such as possessing special geological conditions and special geographical position. -

Active Tectonics of Tehran Area, Iran
J. Basic. Appl. Sci. Res., 2(4)3805-3819, 2012 ISSN 2090-4304 Journal of Basic and Applied © 2012, TextRoad Publication Scientific Research www.textroad.com Active Tectonics of Tehran Area, Iran Mehran Arian1 *, Nooshin Bagha2 1Associate professor, Department of Geology, Science and Research branch, Islamic Azad University, Tehran, Iran 2Ph.D.Student, Department of Geology, Science and Research branch, Islamic Azad University, Tehran, Iran ABSTRACT Tehran area (with 2398.5 km2 area) extended from the east of Damavand volcano to the west of Karaj city. This area is a major part of Tehran province and according to geologic division is a minor part of Alborz zone. This area is under compressive stress and shortening that caused by Arabia – Eurasia Convergence. This situation has confirmed by dominant existence of folded structures and thrust fault system. We have investigated geologic hazards of Tehran area, because this area is the most strategic part of Iran. The major faults have been investigated and have not been found any evidences to existence of north and south Rey faults. In the other hand, active tectonic of this area has been investigated and Mosha fault has been introduced as the most active fault. The high seismic potential has been distinguished by integration of structural geology and active tectonic studies. The evaluation of movement potential of the main faults in the current tectonic regime shows the North Tehran fault has % 90 potential to movement. In addition the hazard potentials of landslides, settlements, volcanism and dams have been introduced. Finally, geologic hazard map has been prepared and has been divided to10 zones with one to four ranking of risk. -

General Overview of Iran Dietary Supplements Market
INDEX INTRODUCTION ......................................................................................................................................................3 GENERAL OVERVIEW OF IRAN DIETARY SUPPLEMENTS MARKET ..........................................................................4 VARIETY OF DSs PRODUCTION IN IRAN ..................................................................................................................5 OPPORTUNITIES IN DSs PRODUCTION IN IRAN ......................................................................................................6 TOTAL SUPPLEMENT PRODUCTION IN IRAN ..........................................................................................................7 TRADE WITH ITALY ..................................................................................................................................................8 ITALIAN PRESENCE IN IRAN ....................................................................................................................................9 IRAN REGISTRATION CODE “IRC” ISSUANCE STEPS ............................................................................................. 10 SOME IMPORTANT TIPS ABOUT OBTAINING IRC ................................................................................................ 11 LIST OF IRANIAN FOOD SUPPLEMENTS IMPORTERS ........................................................................................... 12 THE RELATED TRADE FAIRS OF FOOD AND DIETARY SUPPLEMENTS IN IRAN .................................................... -

Migrations and Social Mobility in Greater Tehran: from Ethnic Coexistence to Political Divisions?
Migrations and social mobility in greater Tehran : from ethnic coexistence to political divisions? Bernard Hourcade To cite this version: Bernard Hourcade. Migrations and social mobility in greater Tehran : from ethnic coexistence to political divisions?. KUROKI Hidemitsu. Human mobility and multi-ethnic coexistence in Middle Eastern Urban societies1. Tehran Aleppo, Istanbul and Beirut. , 102, Research Institute for languages and cultures of Asia and Africa, Tokyo University of Foreign Languages, pp.27-40, 2015, Studia Culturae Islamicae, 978-4-86337-200-9. hal-01242641 HAL Id: hal-01242641 https://hal.archives-ouvertes.fr/hal-01242641 Submitted on 13 Dec 2015 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. LIST OF CONTRIBUTORS Bernard Hourcade is specializing in geography of Iran and Research Director Emeritus of Le Centre national de la recherche scientifique. His publication includes L'Iran au 20e siècle : entre nationalisme, islam et mondialisation (Paris: Fayard, 2007). Aïda Kanafani-Zahar is specializing in Anthropology and Research Fellow of Le Centre national de la recherche scientifique, affiliating to Collège de France. Her publication includes Liban: le vivre ensemble. Hsoun, 1994-2000 (Paris: Librairie Orientaliste Paul Geuthner, 2004). Stefan Knost is specializing in Ottoman history of Syria and Acting Professor of Martin-Luther-Universität Halle-Wittenberg. -
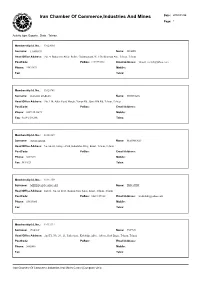
Iran Chamber of Commerce,Industries and Mines Date : 2008/01/26 Page: 1
Iran Chamber Of Commerce,Industries And Mines Date : 2008/01/26 Page: 1 Activity type: Exports , State : Tehran Membership Id. No.: 11020060 Surname: LAHOUTI Name: MEHDI Head Office Address: .No. 4, Badamchi Alley, Before Galoubandak, W. 15th Khordad Ave, Tehran, Tehran PostCode: PoBox: 1191755161 Email Address: [email protected] Phone: 55623672 Mobile: Fax: Telex: Membership Id. No.: 11020741 Surname: DASHTI DARIAN Name: MORTEZA Head Office Address: .No. 114, After Sepid Morgh, Vavan Rd., Qom Old Rd, Tehran, Tehran PostCode: PoBox: Email Address: Phone: 0229-2545671 Mobile: Fax: 0229-2546246 Telex: Membership Id. No.: 11021019 Surname: JOURABCHI Name: MAHMOUD Head Office Address: No. 64-65, Saray-e-Park, Kababiha Alley, Bazar, Tehran, Tehran PostCode: PoBox: Email Address: Phone: 5639291 Mobile: Fax: 5611821 Telex: Membership Id. No.: 11021259 Surname: MEHRDADI GARGARI Name: EBRAHIM Head Office Address: 2nd Fl., No. 62 & 63, Rohani Now Sarai, Bazar, Tehran, Tehran PostCode: PoBox: 14611/15768 Email Address: [email protected] Phone: 55633085 Mobile: Fax: Telex: Membership Id. No.: 11022224 Surname: ZARAY Name: JAVAD Head Office Address: .2nd Fl., No. 20 , 21, Park Sarai., Kababiha Alley., Abbas Abad Bazar, Tehran, Tehran PostCode: PoBox: Email Address: Phone: 5602486 Mobile: Fax: Telex: Iran Chamber Of Commerce,Industries And Mines Center (Computer Unit) Iran Chamber Of Commerce,Industries And Mines Date : 2008/01/26 Page: 2 Activity type: Exports , State : Tehran Membership Id. No.: 11023291 Surname: SABBER Name: AHMAD Head Office Address: No. 56 , Beside Saray-e-Khorram, Abbasabad Bazaar, Tehran, Tehran PostCode: PoBox: Email Address: Phone: 5631373 Mobile: Fax: Telex: Membership Id. No.: 11023731 Surname: HOSSEINJANI Name: EBRAHIM Head Office Address: .No. -
Alphabetical List
ALPHABETICAL LIST 122 123 ALPHABETICAL LIST A I Pages 115 to 158 Pages 281 to 300 B J Pages 158 to 181 Pages 300 to 310 C K Pages 181 to 196 Pages 310 to 331 D L Pages 196 to 212 Pages 331 to 337 E M Pages 212 to 226 Pages 337 to 361 F N Pages 226 to 250 Pages 361 to 379 G O Pages 250 to 261 Pages 379 to 386 H P Pages 261 to 281 Pages 386 to 442 124 Q Y Pages 442 to 444 Pages 556 to 557 R Z Pages 444 to 459 Pages 557 to 560 S Pages 459 to 515 T Pages 515 to 541 U Pages 541 V Pages 541 W Pages 541 to 548 X Pages 548 to 556 125 2MKABLO DIŞ TICARET VE Mehmet Dereli PAZARLAMA A.Ş. Field of activity: able Manufacturer- Special cables- Fire resistant/Halogen SANCAKTEPE MAH, KLAS ALLEY, NO: free Flame retardant cables (LPCB)(IEC 60331, BS 6387 CWZ 8, SILIVRI-ISTANBUL» EN 50200, EN 50362, IEC 60332-3) Instrumentation cables (PVC, PVC-HR, PVC-O, UV resistant, Fire resistant), Marine and Shipboard cables, Control cables, Cathodic Protection cables, Railway cables, Bus cables,.. Tel: 0098-02122228250 Fax: 9.02122E+11 www.2mkablo.com Hall: 38B [email protected], Stand: 2552 [email protected] 3P PRINZ SRL Mrs. Silvia Marianetti Field of activity: Positive Displacement Pumps Manufacturing «Via Enrico Mattei293/R,Mugnano, 55100 Lucca» Tel: +39 0583 491183 Fax: +39 0583 954659 www.3pprinz.com Hall: 38B [email protected] Stand: 2442 3R SOLUTIONS Georg Schulze-Dürr Field of activity: 3R offers a piping software framework and pipe-shop Kleistrasse 39 59073 Hamm Germany turnkey projects. -

A Abbas Abaad, 81 Abkar, 122 Abrahamian, 21, 26, 107, 122 Abu
Index A Ardalan, 123 Abbas Abaad, 81 Arefian, 232, 233, 241 Abkar, 122 Armstrong, 237 Abrahamian, 21, 26, 107, 122 Aronovici, 207 Abu-Lughod, 62 The artists’ house, 55 Achaemenid, 122 Asad Poor, 212 Adair, 243 Asar, 26 Adjdari, 32–35, 40, 41 Ashraf, 21, 26 Adle, 29 The Association of Iranian Architects-Diploma Adlershof, 217 (AIAD), 32 Aghajanian, 91 Astan-e-Qods, 222 Agha Muhammad Khan, 20 Athena, 217, 225 Aghili, 160, 162 Atlas of Tehran Metropolis, 104, 110 Ahar Earthquake, 84 Augé, 20, 23–25, 27, 28 Ahari, 39 Avanessian, 122 Ahvaz, 44, 211 Ayatollah Khomeini, 28, 73 AIAD, 32, 34, 35, 39 Azadi Sport Complex, 123 Akhoondi, 235, 236 Azimi, 56 Akhoundi, 164 Azimzadeh, 188 Alborz, 13 Alemi, 20 B Alexander, 232 Badie, 32, 39 Al-Furqan, 63 Baeten, 217 Aliabadi, 63 Baharestan, 211 Al-Isra, 63, 64 Bahmani brick, 42 Alizamani, 234, 242 Bahraini, 235, 236 Alladian, 24 Bahrainy, 219, 220 Al-Sayyad, 62, 63 Baker, 156 Alstom, 44 Bakhtavar, 55 Amanat, 123 Bam Architectural and Urbanism Council Amili, 67, 68 (BAUC), 238, 241, 243, 244 Aminzadeh, 219, 220 Bam Earthquake, 84 Amirahmadi, 113, 115, 116 Bam Town Council, 236 Amsterdam, 217, 226 Banani, 107 Andisheh, 211 Bani-Etemad, 51, 53 Andrews, 160 Bank-e-Sakhtemani, 38, 39, 41–43 A Night in Tehran, 51 Barakat, 232 Ansoff, 237 Barakpou, 160, 163 Anthropological place, 20, 23–25, 27, 28 Bararpour, 159 © Springer International Publishing Switzerland 2016 249 F.F. Arefian and S.H.I. Moeini (eds.), Urban Change in Iran, The Urban Book Series, DOI 10.1007/978-3-319-26115-7 250 Index Baravat, 241 CIA, 104, -

Comprehensive Plan of Tehran City
Strategic- Structural Comprehensive Plan Of Tehran City Strategic- Structural Comprehensive Plan of Tehran City Translated By: Seyede Elmira MirBahaodin RanaTaghadosi Editor: Kianoosh Zakerhaghighi رسشناسه : شهرداری تهران. مرکز مطالعات و برنامه ریزی شهر تهران Tehran Municipality. Tehran Urban Planning and Research Center عنوان قراردادی : طرح جامع شهر تهران. انگلیسی Comprehensive plan of Tehran city. English عنوان و نام پديدآور : Comprehensive plan of Tehran city / Tehran Urban Planning and Research Center ; translated by Elmira Mir Bahaodin, RanaTaghadosi ; translation and redrawing maps: Anooshiravan Nasser Mostofi. مشخصات نرش : تهران : مرکز مطالعات و برنامه ریزی شهر تهران ، ۱۳۹۴ = ۲۰۱۵م. مشخصات ظاهری : ۷۶ص. : مصور) رنگی(. شابک : 978-600-6080-57-4 وضعیت فهرست نویسی : فیپا يادداشت : انگلیسی. موضوع : شهرسازی -- ایران -- تهران -- طرح و برنامه ریزی موضوع : شهرسازی -- طرح و برنامه ریزی موضوع : شهرسازی -- ایران -- طرح و برنامه ریزی موضوع : توسعه پایدار شهری -- ایران -- تهران شناسه افزوده : مريبهاءالدين، سیده املیرا، ۱۳۶۵ - ، مرتجم شناسه افزوده : MirBahaodin, Seyede Elmira شناسه افزوده : تقدسی، رعنا ، ۱۳۶۱ - ، مرتجم شناسه افزوده : Taghadosi، Rana شناسه افزوده : نارصمستوفی، انوشیروان، ۱۳۵۳ - ، مرتجم شناسه افزوده : Naser Mostofi, Anooshiravan رده بندی کنگره : ۱۳۹۴ ۹۰۴۹۲ت۹۲ الف / HT۱۶۹ رده بندی دیویی : ۳۰۷/۱۲۱۶۰۹۵۵ شامره کتابشناسی ملی : ۴۰۸۶۴۳۰ Tehran Urban Planning and Research Center Secretariat of the Supreme Council for the Monitoring Urban Development of Tehran Comprehensive Plan of Tehran City Translated By: Seyede Elmira MirBahaodin , Rana Taghadosi Editor: Kianoosh Zakerhaghighi First Edition: 2015 Printed copies: 1000 Printed by: Nashr Shahr Institute Price: 50000 Rials Published by: Tehran Urban Planning and Research Center ISBN: 978-600-6080-57-4 All right reserved for publisher. 32. Aghabozorgi st. Shahid Akbari st. Pol-e-Roomi, Shariati Ave. -

Thirty-Five Years of Forced Hijab 2 Justice for Iran
Thirty-five Years of Forced Hijab 2 Justice For Iran Thirty-five Years of Forced Hijab: The Widespread and Systematic Violation of Women’s Rights in Iran Justice For Iran March 2014 email: [email protected] website: www.Justiceforiran.org Cover Design by: Masoumeh Faraji Copyright © Justice for Iran 2014 Reproduction of any or all parts of this document is permissible only with proper citation. Thirty-five Years of Forced Hijab 3 Justice For Iran Contents Introduction ....................................................................................................................................... 4 Chapter 1: A review of the history of hijab enforcement in Iran ................................... 9 Hijab laws in Iran ..................................................................................................................... 10 Chapter 2. Violation of women’s rights due to non-compliance with hijab laws . 15 I. Violation of the principle of non-discrimination, the rights to freedom of expression and belief and access to security ................................................................. 16 Arrest of women charged with failure to observe Islamic hijab laws during the first two decades of the Islamic Republic ........................................................... 16 A cursory examination of statistics on arrests ......................................................... 18 II. Violation of the Prohibition of Torture and Harassment .................................... 24 III. Violation of the Right to Psychological -

Flight from Your Home Country to Tehran We Prepare Ourselves for A
Day 1: Flight from your home country to Tehran We prepare ourselves for a fabulous trip to Great Persia. Arrival to Tehran, after custom formality, meet and assist at airport and transfer to the Hotel. O/N: Tehran Day 2: Tehran After breakfast, full day visit Tehran: Niyavaran Palace, Saad Abad Palace, Darband. O/N: Tehran The NiavaranComplex is a historical complex situated inShemiran , Tehran Greater( Tehran), Iran . It consists of several buildings and monuments built in the Qajar and Pahlavi eras. The complex traces its origin to a garden in Niavaran region, which was used as a summer residence by Fath-Ali Shah of the Qajar Dynasty. A pavilion was built in the garden by the order of Naser ed Din Shah of the same dynasty, which was originally referred to as Niavaran House, and was later renamed Saheb Qaranie House. The pavilion of Ahmad Shah Qajarwas built in the late Qajar period.During the reign of the Pahlavi Dynasty , a modern built mansion named Niavaran House was built for the imperial family of Mohammad Reza Pahlavi. All of the peripheral buildings of the Saheb Qaranie House, with the exception of the Ahmad Shahi Pavilion, were demolished, and the buildings and structures of the present-day complex were built to the north of the Saheb Qaranie House. In the Pahlavi period, the Ahmad Shahi Pavilion served as an exhibition area for the presents from world eaders to the Iranian monarchs. The Sa'dabad Complex is a complex built by the Qajar and Pahlavi monarchs, located in Shemiran, Greater Tehran, Iran. -

Index of Iranian Participant 212 2017 Company Name Page
Index of Iranian participant 212 2017 www.khoushab.com Company Name Page 0ta100 Iranian Industry 228 Abin Gostar Marlik Eng. Group 228 Abtin Sanat Dana Plast 228 Adak Starch 228 Adili Machinery Packing 228 Adonis Teb Laboratory 229 Afshan Sanatavaran Novin 229 Agricaltural Services Holding 229 Agro Food News Agency 229 Ala Sabz Kavir (Jilan) 229 Aladdin Food Ind. 230 Alborz Bahar Machine 230 Alborz Machine Karaj 230 Alborz Sarmayesh 230 Alborz Steel 230 Alia Golestan Food Ind. 231 Almas Film Azarbayjan 231 Almatoz 231 Ama 231 Amad Polymer 231 Arad Science & Technique 232 Ard Azin Neshasteh 232 Ardin Shahd 232 Argon Sanat Sepahan 232 Ari Candy Sabalan Natural & Pure Honey 232 Aria Grap Part 233 Aria Plastic Iranian 233 Arian Car Pack 233 Arian Milan 233 Arian Zagros Machine 233 Arkan Felez 234 Armaghan Behshahd Chichest (Mirnajmi Honey) 234 telegram.me/golhaco instagram:@golhaco www.golhaco.ir صدای مشرتی: 5-66262701 تلفکس: 66252490-4 club.golhaco.ir پس از هر طلوع چاشنی زندگی تان می شویم 213 www.khoushab.com 2017 Company Name Page Armaghan Chashni Toos (Arshia) 234 Armaghan Dairy (Manimas) 234 Arman Goldasht 234 Armen Goosht 235 Arvin Bokhar Heating Ind. 235 Asal Dokhte Shahd 235 Asan Kar Ind. Group 235 Asan Pack (Asan Ghazvin Pack & Print Ind.) 235 Ashena Lable 236 Ashianeh Sabz Pardisan 236 Ashkan Mehr Iranian 236 Asia Borj 236 Asia Cap Band 236 Asia Shoor 237 Atlas Tejarat Saina 237 Atrin Protein 237 Ava 237 Aytack Commercial 237 Azar Halab 238 Azar Yeshilyurt 238 Azin Masroor 238 Azooghe Shiraz 238 Bahraman Saffron 238 Barzegar Magazine 239 Barzin Sanat Koosha 239 Baspar Pishrafteh Sharif 239 Behafarin Behamin 239 Behban Shimi 239 Beheshtghandil 240 Behfar Machine Sahand 240 Behin Azma Shiraz Eng. -

Tehran University of Medical Science) Page 146
19 18 ISSN 1839-0188 September 2017 - Volume 15, Issue 7 Cultural competency: a concept analysis in TUMS (Tehran University of Medical Science) page 146 MIDDLE EAST JOURNAL OF FAMILY MEDICINE • VOLUME 7, ISSUE 10 EDITORIAL Qidwai, W & Jawaid, M led a population- Boroujeni A.S et al reviewed new meth- From the Editor based cross sectional survey to estimate ods in the treatment renal failure in the frequency of hyperuricemia in Pa- patients with multiple myeloma. The Chief Editor: kistan. The frequency of hyperuricemia authors reviewed common and ad- A. Abyad was 39% , with 90.8% symptomatic. The vanced treatments (immunotherapy, cell MD, MPH, AGSF, AFCHSE authors concluded that the burden of therapy, new therapies based on genetic Email: [email protected] hyperuricemia together with increasing engineering) in these patients and to Ethics Editor and Publisher burden of metabolic syndrome, obesity, consider this disease in an immunologi- Lesley Pocock ischemic heart disease and chronic kid- cal view. medi+WORLD International ney disease is becoming alarming. AUSTRALIA Vaezi , A.A et al investigate the effect of Jokari , M & Gorjian, Z led an experimen- endotracheal tube cuff pressure on sore Email: tal study evaluating The Effect of Educa- throat, hoarseness and cough in patients [email protected] tional Training on Nurses’ Clinical Func- with cardiac artery bypass surgery. The ............................................................................ tion of Cardiopulmonary Resuscitation . authors found that endotracheal tube This issue is rich with papers from the The authors concluded that the nurses cuff pressure reduce the severity of coro- region. The topics vary from clinical of Taleghani Hospital had experience of nary artery bypass graft surgery patients research, to case series, population CPR guidelines at the significant level cough and sore throat so in order to studies and educational research.