Theory and Design of PL (CS 538) February 3, 2020
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Questions for Ruby Gems
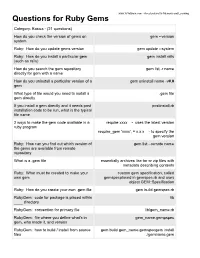
www.YoYoBrain.com - Accelerators for Memory and Learning Questions for Ruby Gems Category: Basics - (21 questions) How do you check the version of gems on gem --version system Ruby: How do you update gems version gem update --system Ruby: How do you install a particular gem gem install rails (such as rails) How do you search the gem repository gem list -r name directly for gem with a name How do you uninstall a particular version of a gem uninstall name -v#.# gem What type of file would you need to install a .gem file gem directly If you install a gem directly and it needs post postinstall.rb installation code to be run, what is the typical file name 2 ways to make the gem code available in a require xxxx - uses the latest version ruby program require_gem 'xxxx', = x.x.x - to specify the gem version Ruby: How can you find out which version of gem list --remote name the gems are available from remote repository What is a .gem file essentially archives like tar or zip files with metadata describing contents Ruby: What must be created to make your custom gem specification, called own gem gemspecplaced in gemspec.rb and uses object GEM::Specification Ruby: How do you create your own .gem file gem build gemspec.rb RubyGem: code for package is placed within lib ____ directory RubyGem: convention for primary file lib/gem_name.rb RubyGem: file where you define what's in gem_name.gempspec gem, who made it, and version RubyGem: how to build / install from source gem build gem_name.gemspecgem install files ./gemname.gem RubyGem: how to push a created gem to gem push gem_name-0.0.0.gem RubyGems.org RubyGems: how to detect a gem on gem list -r gem_name RubyGems.org RubyGems: convention for adding modules / make a directory inside lib with same name classes to gem as gemlib/gem_name/ . -

Automating Configuration N49(PDF)
Automating Network Configuration Brent Chapman Netomata, Inc. [email protected] www.netomata.com NANOG 49 — 13 June 2010 Copyright © 2010, Netomata, Inc. All Rights Reserved. Introduction Who I am What I'm here to talk about 2 Copyright © 2010, Netomata, Inc. All Rights Reserved. Why automate network configuration? Because automated networks are More reliable Easier to maintain Easier to scale 3 Copyright © 2010, Netomata, Inc. All Rights Reserved. For example... Imagine you're managing a moderately complex web site Multiple real and virtual hosts Several "environments" (production, testing, development, etc.) Separate VLAN for each environment 4 Copyright © 2010, Netomata, Inc. All Rights Reserved. For example... What networking devices & services need to be managed? Routers Switches Load Balancers Firewalls Real-time status monitoring (i.e., Nagios) Long-term usage monitoring (i.e., MRTG) 5 Copyright © 2010, Netomata, Inc. All Rights Reserved. For example... How to add new virtual host to existing load balancer pool? Set up host itself, using Puppet or cfengine or whatever Add host to VLAN defs on switches Add host to ACLs on routers Add host to pool on load balancers Add host to NAT and ACLs on firewalls Add host to real-time monitoring (i.e., Nagios) Add host to usage monitoring (i.e., MRTG) 6 Copyright © 2010, Netomata, Inc. All Rights Reserved. For example... What's the problem with doing all that by hand? You have to remember how to manage all those very different devices (and you probably don't do it very often) It takes a lot of time Every step is a chance to make a mistake You might get distracted, and never finish Over time, these small mistakes add up, leading to inconsistent networks that are unreliable and difficult to troubleshoot 7 Copyright © 2010, Netomata, Inc. -

Symbols & Numbers A
ruby_02.book Page 267 Thursday, May 10, 2007 4:12 PM INDEX Symbols & Numbers \ (backslash), in regular expression, for literal characters, 144 %Q for instantiating Strings, 23, \W, in regular expression, for 108–109, 215–216, 219, 239, whitespace, 66 245, 248–250 { } (braces) %w for instantiating Arrays, 47, for blocks, 28 113, 115 for declaring Hash, 42 & (ampersand), for expressing blocks {x}, in regular expression, 79 and Procs, 105–106 - method (Hash), 93 ! (exclamation point), for destructive ||= operator, 77–78, 127 methods, 20, 22–23 | (pipe) character, in regular || (or) operator, 17 expression, 56 # character + method of Integers and Strings, 3–4 for comments, 14 + (plus sign), in regular for instance method, 234 expression, 62 #{} for wrapping expression to be = (equal sign), for assigning value to interpolated, 23 variable, 9 #! (shebang), 47 == operator, for equality testing, 14 $ (dollar sign), for bash prompt, 19 =begin rdoc, 22 * (asterisk), in irb prompt, 8 =end, 22 ** (asterisk doubled), for “to the <=> method (Comparable), 145, power of,” 72 150–151 /\d+/ in regular expression, for digits <% and %> tags, 211 only, 79 <%= tag, for printing expression, 214 :needs_data Symbol key, 116 99bottles.rb script, 20–25 :nitems Symbol key, 116 :unless0th Symbol key, 116 ? (question mark) A in predicate method names, 22 actionpack, warnings related to, 226 in regular expression, for optional Active Record, Rails dependence expressions, 144 on, 227 @ sign, for instance variable, 21–22 Agile Web Development with Rails @@ sign, for class -
Benjamin M. Ward (703) 336 9706 [email protected]
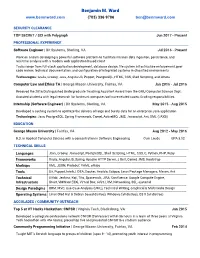
Benjamin M. Ward www.benmward.com (703) 336 9706 [email protected] SECURITY CLEARANCE TOP SECRET / SCI with Polygraph Jun 2017 - Present PROFESSIONAL EXPERIENCE Software Engineer | Bit Systems, Sterling, VA Jul 2016 - Present Work on a team developing a powerful software platform to facilitate mission data ingestion, persistence, and real-time analysis with a modern web application based client Tasks range from full-stack application development, database design, file system infrastructure enforcement, peer code review, technical documentation, and configuration of integrated systems in classified environments Technologies: Grails, Groovy, Java, AngularJS, Puppet, PostgreSQL, HTML, CSS, Shell Scripting, and others Computer Law and Ethics TA | George Mason University, Fairfax, VA Jan 2016 - Jul 2016 Received the 2016 Distinguished Undergraduate Teaching Assistant Award from the GMU Computer Science Dept. Assisted students with legal research for landmark computer/software related cases; Grading responsibilities Internship (Software Engineer) | Bit Systems, Sterling, VA May 2015 - Aug 2015 Developed a caching system to optimize the delivery of large and bursty data for an enterprise Java application Technologies: Java, PostgreSQL, Spring Framework, Camel, ActiveMQ, JMS, Javascript, Ant, XML (JAXB) EDUCATION George Mason University | Fairfax, VA Aug 2012 - May 2016 B.S. in Applied Computer Science with a concentration in Software Engineering Cum Laude GPA 3.52 TECHNICAL SKILLS Languages Java, Groovy, Javascript, PostgreSQL, Shell -

Zentrale Verwaltung Mit Facter, Puppet Und Augeas
System-Management-Trio Zentrale Verwaltung mit facter, puppet und augeas Verwaltung mit facter, puppet und augeas © SpeedPartner GmbH Seite: 1 / 34 GUUG Frühjahrsfachgespräch, 01.03.2012 Über den Vortrag Aufbau / Ziele: ● Einführung / Überblick ● Begriffsklärung ● Aufbau / Arbeitsweise von Manifests ● Templates, Klassen, Typen, Module ● Facter: Umgebungsparameter ermitteln ● Augeas: Konfigurationen bearbeiten ● Client-Server-Betrieb ● Arbeit mit mehreren Umgebungen ● Links / Hilfen Verwaltung mit facter, puppet und augeas © SpeedPartner GmbH Seite: 2 / 34 GUUG Frühjahrsfachgespräch, 01.03.2012 Über mich ● Stefan Neufeind ● Mit-Geschäftsführer der SpeedPartner GmbH aus Neuss ein Internet-Service-Provider (ISP) ● Individuelle TYPO3-Entwicklungen ● Hosting, Housing, Managed Services ● Domains / Domain-Services ● IPv6, DNSSEC, ... ● Aktive Mitarbeit im Community-Umfeld (PHP/PEAR, TYPO3, Linux) ● Freier Autor für z.B. t3n, iX, Internet World, ... Verwaltung mit facter, puppet und augeas © SpeedPartner GmbH Seite: 3 / 34 GUUG Frühjahrsfachgespräch, 01.03.2012 Aufgabenstellung Alltägliche Administrationsaufgaben für ein (Server-)System Basisinstallation Fehler bei Ausführung von Zugänge „Standard-Aufgaben“? Backup Monitoring Fehlersuche / Einrichtung / Fehlerkorrektur Konzeptfehler? Konfiguration Netzwerk Fehler durch die Systemstatistiken „Sonderlösungen“? Architektur Virtuell? Individuelle Anpassungen Aufgaben RAID? Verwaltung mit facter, puppet und augeas © SpeedPartner GmbH Seite: 4 / 34 GUUG Frühjahrsfachgespräch, 01.03.2012 Aufgabenstellung -

Pipenightdreams Osgcal-Doc Mumudvb Mpg123-Alsa Tbb
pipenightdreams osgcal-doc mumudvb mpg123-alsa tbb-examples libgammu4-dbg gcc-4.1-doc snort-rules-default davical cutmp3 libevolution5.0-cil aspell-am python-gobject-doc openoffice.org-l10n-mn libc6-xen xserver-xorg trophy-data t38modem pioneers-console libnb-platform10-java libgtkglext1-ruby libboost-wave1.39-dev drgenius bfbtester libchromexvmcpro1 isdnutils-xtools ubuntuone-client openoffice.org2-math openoffice.org-l10n-lt lsb-cxx-ia32 kdeartwork-emoticons-kde4 wmpuzzle trafshow python-plplot lx-gdb link-monitor-applet libscm-dev liblog-agent-logger-perl libccrtp-doc libclass-throwable-perl kde-i18n-csb jack-jconv hamradio-menus coinor-libvol-doc msx-emulator bitbake nabi language-pack-gnome-zh libpaperg popularity-contest xracer-tools xfont-nexus opendrim-lmp-baseserver libvorbisfile-ruby liblinebreak-doc libgfcui-2.0-0c2a-dbg libblacs-mpi-dev dict-freedict-spa-eng blender-ogrexml aspell-da x11-apps openoffice.org-l10n-lv openoffice.org-l10n-nl pnmtopng libodbcinstq1 libhsqldb-java-doc libmono-addins-gui0.2-cil sg3-utils linux-backports-modules-alsa-2.6.31-19-generic yorick-yeti-gsl python-pymssql plasma-widget-cpuload mcpp gpsim-lcd cl-csv libhtml-clean-perl asterisk-dbg apt-dater-dbg libgnome-mag1-dev language-pack-gnome-yo python-crypto svn-autoreleasedeb sugar-terminal-activity mii-diag maria-doc libplexus-component-api-java-doc libhugs-hgl-bundled libchipcard-libgwenhywfar47-plugins libghc6-random-dev freefem3d ezmlm cakephp-scripts aspell-ar ara-byte not+sparc openoffice.org-l10n-nn linux-backports-modules-karmic-generic-pae -

Flycheck Release 32-Cvs
Flycheck Release 32-cvs Aug 25, 2021 Contents 1 Try out 3 2 The User Guide 5 2.1 Installation................................................5 2.2 Quickstart................................................7 2.3 Troubleshooting.............................................8 2.4 Check buffers............................................... 12 2.5 Syntax checkers............................................. 14 2.6 See errors in buffers........................................... 18 2.7 List all errors............................................... 22 2.8 Interact with errors............................................ 24 2.9 Flycheck versus Flymake........................................ 27 3 The Community Guide 33 3.1 Flycheck Code of Conduct........................................ 33 3.2 Recommended extensions........................................ 34 3.3 Get help................................................. 37 3.4 People.................................................. 37 4 The Developer Guide 45 4.1 Developer’s Guide............................................ 45 5 The Contributor Guide 51 5.1 Contributor’s Guide........................................... 51 5.2 Style Guide................................................ 54 5.3 Maintainer’s Guide............................................ 57 6 Indices and Tables 63 6.1 Supported Languages.......................................... 63 6.2 Glossary................................................. 85 6.3 Changes................................................. 85 7 Licensing 93 7.1 Flycheck -

Jason Fraley
CAREER PROFILE I have an ambitious personality with over 25 years of experience in the computer and information technology field, seeking a leadership position in a dynamic business environment where my unique skill Jason set can be used to its potential. I strive to make sure any given technology strategy is not in place for its own sake, but exists to serve Fraley the overall business requirements. I have a deep-seated passion for this industry and believe that nothing is impossible. My ability to envision of the big picture while maintaining a detailed understanding of the graphic detail Technology Czar and has helped me to repeatedly make decisions that extract 80% of the value with 20% of the cost. Engineer of Things I endeavor to fulfill the corporate mission, or help invent a new one. I am very results driven, and have been recognized for taking on major and groundbreaking initiatives. Adaptation to rapidly changing environmental factors, resolution of critical issues has helped me to ✉ [email protected] I live and breathe technology, and do it pretty well. � —- —- —— Most recent version of this resume available here: � chmod-xchmod.com � linkedin.com/in/jason-fraley � oelbrenner EXPERIENCE SKILLS AND PROFICIENCY Vice President Engineering 2018 - 2019 KnowBe4, Clearwater FL Reporting to the CTO, I grew the Development and Quality Assurance divisions from under 20 to over 60 people. I built a lean engineering organization from the ground up focused on high-quality, extremely scalable software platforms that were instrumental in propelling KnowBe4 to a 2019 billion dollar valuation in the top right corner of the Gartner Magic Quadrant. -

Beginning Ruby on Rails.Pdf
01_069155 ffirs.qxp 10/23/06 8:02 PM Page i Beginning Ruby on Rails™ 01_069155 ffirs.qxp 10/23/06 8:02 PM Page ii 01_069155 ffirs.qxp 10/23/06 8:02 PM Page iii Beginning Ruby on Rails™ Steven Holzner 01_069155 ffirs.qxp 10/23/06 8:02 PM Page iv Beginning Ruby on Rails™ Published by Wiley Publishing, Inc. 10475 Crosspoint Boulevard Indianapolis, IN 46256 www.wiley.com Copyright © 2007 by Wiley Publishing, Inc., Indianapolis, Indiana Published simultaneously in Canada ISBN-13: 978-0-470-06915-8 ISBN-10: 0-470-06915-5 Manufactured in the United States of America 10 9 8 7 6 5 4 3 2 1 1B/QZ/RR/QW/IN Library of Congress Catalog Control Number: 2006030329 No part of this publication may be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, scanning or otherwise, except as permitted under Sections 107 or 108 of the 1976 United States Copyright Act, without either the prior written permission of the Publisher, or authorization through payment of the appropriate per-copy fee to the Copyright Clearance Cen- ter, 222 Rosewood Drive, Danvers, MA 01923, (978) 750-8400, fax (978) 646-8600. Requests to the Publisher for permission should be addressed to the Legal Department, Wiley Publishing, Inc., 10475 Crosspoint Blvd., Indi- anapolis, IN 46256, (317) 572-3447, fax (317) 572-4355, or online at http://www.wiley.com/go/permissions. LIMIT OF LIABILITY/DISCLAIMER OF WARRANTY: THE PUBLISHER AND THE AUTHOR MAKE NO REPRESENTATIONS OR WARRANTIES WITH RESPECT TO THE ACCURACY OR COMPLETENESS OF THE CONTENTS OF THIS WORK AND SPECIFICALLY DISCLAIM ALL WARRANTIES, INCLUDING WITHOUT LIMITATION WARRANTIES OF FITNESS FOR A PARTICULAR PURPOSE. -

Extendingruby1.9
Extending Ruby 1.9 Writing Extensions in C Dave Thomas with Chad Fowler Andy Hunt The Pragmatic Bookshelf Raleigh, North Carolina Dallas, Texas Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks. Where those designations appear in this book, and The Pragmatic Programmers, LLC was aware of a trademark claim, the designations have been printed in initial capital letters or in all capitals. The Pragmatic Starter Kit, The Pragmatic Programmer, Pragmatic Programming, Pragmatic Bookshelf and the linking g device are trademarks of The Pragmatic Programmers, LLC. Every precaution was taken in the preparation of this book. However, the publisher assumes no responsibility for errors or omissions, or for damages that may result from the use of information (including program listings) contained herein. Our Pragmatic courses, workshops, and other products can help you and your team create better software and have more fun. For more information, as well as the latest Pragmatic titles, please visit us at http://www.pragprog.com. Copyright © 2010 The Pragmatic Programmers, LLC. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form, or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior consent of the publisher. Printed in the United States of America. ISBN-10: ISBN-13: Printed on acid-free paper. 1.0 printing, November 2010 Version: 2010-11-11 Contents 1 Introduction 5 2 ExtendingRuby 6 2.1 Your First Extension ........................... 6 2.2 Ruby Objects in C ............................ 9 2.3 TheThreadingModel ......................... -

Towards Left Duff S Mdbg Holt Winters Gai Incl Tax Drupal Fapi Icici
jimportneoneo_clienterrorentitynotfoundrelatedtonoeneo_j_sdn neo_j_traversalcyperneo_jclientpy_neo_neo_jneo_jphpgraphesrelsjshelltraverserwritebatchtransactioneventhandlerbatchinsertereverymangraphenedbgraphdatabaseserviceneo_j_communityjconfigurationjserverstartnodenotintransactionexceptionrest_graphdbneographytransactionfailureexceptionrelationshipentityneo_j_ogmsdnwrappingneoserverbootstrappergraphrepositoryneo_j_graphdbnodeentityembeddedgraphdatabaseneo_jtemplate neo_j_spatialcypher_neo_jneo_j_cyphercypher_querynoe_jcypherneo_jrestclientpy_neoallshortestpathscypher_querieslinkuriousneoclipseexecutionresultbatch_importerwebadmingraphdatabasetimetreegraphawarerelatedtoviacypherqueryrecorelationshiptypespringrestgraphdatabaseflockdbneomodelneo_j_rbshortpathpersistable withindistancegraphdbneo_jneo_j_webadminmiddle_ground_betweenanormcypher materialised handaling hinted finds_nothingbulbsbulbflowrexprorexster cayleygremlintitandborient_dbaurelius tinkerpoptitan_cassandratitan_graph_dbtitan_graphorientdbtitan rexter enough_ram arangotinkerpop_gremlinpyorientlinkset arangodb_graphfoxxodocumentarangodborientjssails_orientdborientgraphexectedbaasbox spark_javarddrddsunpersist asigned aql fetchplanoriento bsonobjectpyspark_rddrddmatrixfactorizationmodelresultiterablemlibpushdownlineage transforamtionspark_rddpairrddreducebykeymappartitionstakeorderedrowmatrixpair_rddblockmanagerlinearregressionwithsgddstreamsencouter fieldtypes spark_dataframejavarddgroupbykeyorg_apache_spark_rddlabeledpointdatabricksaggregatebykeyjavasparkcontextsaveastextfilejavapairdstreamcombinebykeysparkcontext_textfilejavadstreammappartitionswithindexupdatestatebykeyreducebykeyandwindowrepartitioning -

The Druby Book(2012).Pdf
What Readers Are Saying About The dRuby Book The dRuby Book is a fantastic introduction to distributed programming in Ruby for all levels of users. The book covers all aspects of dRuby, including the principles of distributed programming and libraries and techniques to make your work easier. I recommend this book for anyone who is interested in distributed program- ming in Ruby and wants to learn the basics all the way to advanced process coordination strategies. ➤ Eric Hodel Ruby committer, RDoc and RubyGems maintainer dRuby is the key component that liberates Ruby objects from processes and machine platforms. Masatoshi himself explains its design, features, case studies, and even more in this book. ➤ Yuki “Yugui” Sonoda Ruby 1.9 release manager dRuby naturally extends the simplicity and power Ruby provides. Throughout this book, Rubyists should be able to enjoy a conversation with dRuby that makes you feel as if your own thoughts are traveling across processes and networks. ➤ Kakutani Shintaro RubyKaigi organizer, Ruby no Kai Any programmer wanting to understand concurrency and distributed systems using Ruby should read this book. The explanations and example code make these topics approachable and interesting. ➤ Aaron Patterson Ruby and Ruby on Rails core committer A fascinating and informative look at what is classically a total pain in the neck: distributed object management and process coordination on a single machine or across a network. ➤ Jesse Rosalia Senior software engineer The dRuby Book Distributed and Parallel Computing with Ruby Masatoshi Seki translated by Makoto Inoue The Pragmatic Bookshelf Dallas, Texas • Raleigh, North Carolina Many of the designations used by manufacturers and sellers to distinguish their products are claimed as trademarks.