Algorithmic Cost Allocation Games: Theory and Applications
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Factsheet Jeugdsportmonitor Overijssel 2016
Colofon Jeugdsportmonitor Overijssel 2016 Provinciaal onderzoek naar sport, bewegen en leefstijl onder jongeren (4 tot en met 17 jaar) Mei 2017 In opdracht van de provincie Overijssel en de deelnemende gemeenten Drs. Marieke van Vilsteren Sportservice Overijssel Hogeland 10 8024 AZ Zwolle www.sportserviceoverijssel.nl Overname van dit rapport of gedeelten daaruit is toegestaan, mits de bron wordt vermeld. Algemene informatie In het najaar van 2016 is voor de derde keer de Jeugdsportmonitor uitgevoerd door Sportservice Overijssel in opdracht van de provincie Overijssel en in samenwerking met Overijsselse gemeenten. De Jeugdsportmonitor geeft een goed beeld van het sport- en beweeggedrag en de leefstijl van jeugd en jongeren in Overijssel (4 tot en met 17 jaar). De provinciale resultaten worden in deze factsheet besproken. Gemeentelijke cijfers staan weergegeven in het tabellenboek en de gemeentelijke factsheets. Sportservice Overijssel Sportservice Overijssel is het provinciale kenniscentrum voor sport en bewegen in de Respons Ruim provincie Overijssel. Wij willen met onze kennis de verschillende maatschappelijke partijen hand- 15.000 vatten aanreiken, zodat investeringen in sport en bewegen efficiënt en effectief worden ingezet. leerlingen hebben Daarbij maken we gebruik van bestaande kennis, meegedaan aan de maar ontwikkelen we ook monitoren voor nog Jeugdsportmonitor! ontbrekende gegevens. Sportservice Overijssel zorgt voor regelmatige herhaling van onderzoek, een vereiste om ontwikkelingen nauwlettend te kunnen volgen en trends te kunnen waarnemen. Sportservice Overijssel heeft als doel om zoveel mogelijk inwoners de kans te geven (blijvend) te 52% sporten en te bewegen. In navolging op het rapport ‘Fit en Gezond in Overijssel’, een primair onderwijs tweejaarlijks monitoronderzoek naar sport, bewegen en leefstijl onder volwassenen, is in 2012 48% door Sportservice Overijssel ook een tweejaarlijkse voortgezet onderwijs monitor opgezet om sport, bewegen en leefstijl van de Overijsselse jeugd en jongeren in kaart te brengen: de Jeugdsportmonitor. -

Besluit Interne Relatieve Bevoegdheid Rechtbank Overijssel Vastgesteld 11 Maart 2014
Besluit interne relatieve bevoegdheid rechtbank Overijssel Vastgesteld 11 maart 2014 Nadere regels als bedoeld in artikel 6 van het zaaksverdelingsreglement 1. Indien in het schema onder punt 2 van het zaaksverdelingsreglement in de kolom “loket” één locatie is vermeld, dienen (de stukken inzake) deze zaken op de desbetreffende locatie te worden ingediend. 2. Indien in het schema onder punt 2 van het zaaksverdelingsreglement in de kolom “loket” meerdere locaties zijn vermeld bij een categorie zaken, zijn voor de beantwoording van de vraag bij welke locatie (de stukken inzake) deze zaken moeten worden ingediend, de wettelijke bevoegdheidsregels van overeenkomstige toepassing. 3. Voor het dagvaarden in een zaak over huur, arbeid, pacht, consumentenaangelegenheden, alsmede voor het indienen van civiele vorderingen tot € 25.000 en verzoeken tot het instellen van bewind, mentorschap, voogdij of curatele, bevatten de in bijlage 1 genoemde locaties de daarbij genoemde gemeenten. 4. Voor het indienen van alle andere zaken bevatten de in bijlage 2 genoemde locaties de daarbij genoemde gemeenten. 5. Kan aan de hand van het vorenstaande niet worden vastgesteld waar een zaak moet worden ingediend, dan moet de zaak worden ingediend bij de locatie Zwolle. 6. De rechter-commissaris in strafzaken van de locatie waar een zaak volgens dit besluit moet worden ingediend, kan zijn werkzaamheden overdragen aan een rechter-commissaris op een andere locatie. Vastgesteld door het gerechtsbestuur te Zwolle op 11 maart 2014 datum 11 maart 2014 pagina 2 van 3 BIJLAGE -

Kantoor Op De Lijn Arnhem - Oldenzaal
PORTLIJST VOOR HET SPOORWEG - KANTOOR OP DE LIJN ARNHEM - OLDENZAAL Circulaire 700 (16 juli 1867) AANWIJZING VAN DE POSTKANTOREN EN VAN DE STATIONS OP DEN SPOORWEG ARNHEM - OLDENZAAL, TUSSCHEN WELKE, ALS OP EENEN AFSTAND VAN 30 NEDERLANDSCHE MIJLEN OF MINDER VAN ELKANDER GELEGEN ZIJNDE, HET PORT 5 CENTS VOOR DEN ENKELEN BRIEF BEDRAAGT. NOTA. Het port tusschen alle de overige Postkantoren en Stations. Die niet in betrekking tot elkander op deze Lijst vermeld staan, bedraagt 10 cents voor den enkelen brief. POSTKANTOREN of STATIONS POSTKANTOREN of STATIONS van VERZENDING van BESTEMMING ARNHEM Apeldoorn Brummen Doesborgh Doetinchem Grave Nijmegen Veenendaal Velp Wageningen Zevenaar Zutphen Dieren Duiven Ede de Steeg Westervoort Wolfheze VELP Apeldoorn Arnhem Brummen Doesborgh Doetinchem Grave Nijmegen Terborgh Veenendaal Wageningen Zevenaar Zutphen Dieren Duiven Ede de Steeg Westervoort Wolfheze BRUMMEN Apeldoorn Arnhem Deventer Doesborgh Doetinchem Terborgh Velp Zevenaar Zutphen Dieren Duiven Laren Lochem Markelo de Steeg Westervoort Wolfheze ZUTPHEN Apeldoorn Arnhem Brummen Deventer Doesborgh Doetinchem Goor Terborgh Velp Zevenaar Zutphen Dieren Duiven Laren Lochem Markelo de Steeg Westervoort LAREN Apeldoorn Brummen Deventer Doesborgh Doetinchem Goor Terborgh Zutphen Delden Dieren Lochem Markelo de Steeg LOCHEM Almelo Brummen Deventer Doesborgh Doetinchem Goor Hengelo Terborgh Winterswijk Zutphen Delden Dieren Laren Markelo de Steeg MARKELO Almelo Brummen Deventer Doetinchem Enschede Goor Hengelo Winterswijk Zutphen Delden Laren Lochem GOOR Almelo zie Circ. 704 Deventer Enschede Hengelo Oldenzaal (Winterswijk) zie Circ. 704) Zutphen Delden Laren Lochem Markelo DELDEN Almelo Enschede Goor Hengelo Oldenzaal Laren Lochem Markelo HENGELO Almelo Enschede Goor Oldenzaal Delden Lochem Markelo OLDENZAAL Almelo Enschede Goor Hengelo Delden CIRCULAIRE 704 (1sten October 1867) Art.6 Het is nader gebleken dat de juiste afstand, hemelsbreedte, tusschen Goor en Winterswijk 30.525 mijl bedraagt. -

Humanities Computing: A
Humanities Computing: A Federation of Disciplines John Nerb onne Alfa-Informatica University of Groningen [email protected] http://www.let.rug.nl/alfa/ Series: Is Humanities Computing an Academic Discipline? Organized by John Unsworth University of Virginia Oct. 29, 1999 RROPQR IJ Federation KL MN Federation Thesis: Humanities Computing (HC) is not a discipline (yet), but a federation of co op erating disciplines. a discipline is demarcated by a subject matter a range of analytical techniques one or more comp eting theories where appropriate, practical applications caution: these are claims ab out elds, not ab out every piece of work, or every scholar's cumulative work HC has neither coherent subject matter nor theory (apart from its comp onents) RROPQR 1 IJ Vision KL MN Federation Humanities Computing is ...die Fortsetzung der Geisteswissen- schaften mit anderen Mitteln. (with ap ologies to Clausewitz, Battus). unsurprising but signicant HC must engage traditional Humanities HC's primary value is within traditional Humanities which traditional Humanities problems have we solved? opp osed to view that HC's purp ose is to understand digital culture using humanities metho ds studies comparing printing press to computers Electronic Incunabula (Nerb onne, 1995) linguistic studies of computer-mediated communication literary studies of hyp ertext vs. planar text recent prop osal from Dutch Science CouncilWTR interesting, but not HC's job RROPQR 2 IJ Parallel? KL MN Federation in general, scholarship makes use of all available -

Overijsselaars Gezocht
Overijsselaars gezocht Inhoud 1. Overijsselaars gezocht ............................................................................. 7 Inleiding ................................................................................................................................... 7 Vormen van onderzoek ............................................................................................................ 8 Vastleggen van gegevens .......................................................................................................... 9 Is er al onderzoek gedaan? ..................................................................................................... 10 Genealogie en internet ........................................................................................................... 12 Archiefbewaarplaatsen in Overijssel ....................................................................................... 13 Archiefbezoek: hoe gaat dat? ................................................................................................. 15 Literatuur ............................................................................................................................... 16 Online verwijzingen ................................................................................................................ 16 2. Het begin van het archiefonderzoek ...................................................... 17 Inleiding ................................................................................................................................ -

International Rate Centers for Virtual Numbers
8x8 International Virtual Numbers Country City Country Code City Code Country City Country Code City Code Argentina Bahia Blanca 54 291 Australia Brisbane North East 61 736 Argentina Buenos Aires 54 11 Australia Brisbane North/North West 61 735 Argentina Cordoba 54 351 Australia Brisbane South East 61 730 Argentina Glew 54 2224 Australia Brisbane West/South West 61 737 Argentina Jose C Paz 54 2320 Australia Canberra 61 261 Argentina La Plata 54 221 Australia Clayton 61 385 Argentina Mar Del Plata 54 223 Australia Cleveland 61 730 Argentina Mendoza 54 261 Australia Craigieburn 61 383 Argentina Moreno 54 237 Australia Croydon 61 382 Argentina Neuquen 54 299 Australia Dandenong 61 387 Argentina Parana 54 343 Australia Dural 61 284 Argentina Pilar 54 2322 Australia Eltham 61 384 Argentina Rosario 54 341 Australia Engadine 61 285 Argentina San Juan 54 264 Australia Fremantle 61 862 Argentina San Luis 54 2652 Australia Herne Hill 61 861 Argentina Santa Fe 54 342 Australia Ipswich 61 730 Argentina Tucuman 54 381 Australia Kalamunda 61 861 Australia Adelaide City Center 61 871 Australia Kalkallo 61 381 Australia Adelaide East 61 871 Australia Liverpool 61 281 Australia Adelaide North East 61 871 Australia Mclaren Vale 61 872 Australia Adelaide North West 61 871 Australia Melbourne City And South 61 386 Australia Adelaide South 61 871 Australia Melbourne East 61 388 Australia Adelaide West 61 871 Australia Melbourne North East 61 384 Australia Armadale 61 861 Australia Melbourne South East 61 385 Australia Avalon Beach 61 284 Australia Melbourne -

Inventaris De Oude Archieven Van Oldenzaal 1296-1810
. DE OUDE ARCHIEVEN VAN OLDENZAAL ~~ ~ ,, DOOR Dr~ W~ J~ FORMSM m 1938 INHOUD. Blz. Inleiding 5 Inventaris 10 Archief van het stadsbestuur tot 1811 10 I. Stukken van algeroeenen aard 10 II. Privilegiën en rechten 10 III. Inrichting en samenstelling van het stadsbestuur . 12 IV. Personeel 13 V. Financiën 1Z a. Schattingen 13 b. Landsmiddelen 14 1. Kohieren 14 2. Rekeningen 15 3. Andere stukken 16 c. Stedelijke financiën 18 1. In het algemeen 18 2. Rekeningen en kohieren 19 3. Schuldbekentenissen 19 4. Verpachtingen 20 5. Burgergelden 20 6. Eigendommen in het algemeen 20 7. Oldenzaalsche veen 22 8. Bank van leening 22 9. Postwagen 22 VI. Bevolking 23 VII. Militaire zaken 24 VIII. Openbare orde en veiligheid 25 IX. Openbare werken 27 x. Bedrijven 27 XI. Kerkelijke zaken 28 XII. Schoolwezen 29 a. Latijnsche school 29 b. Duitsche school 31 XIII. Armenstaat 31 a. Financieel beheer in het algemeen 31 b. Vaste goederen 34 c. Schuldbekentenissen 39 d. Onderhoud van de armen 41 Varia 41 Stukken van den richter van het landgericht 42 Archief van gecommitteerde goedsheeren van het gericht (kerSipel) Oldenzaal 43 Archief van den kerkeraad der Ned. Herv. Gemeente tot 1816 46 Regestenlijst 50 Index 101 Kaart 5 DE OUDE ARCHIEVEN VAN OLDENZAAL. Inleiding. Het oudste. stuk, dat tot het stedelijk archief behoort, dateert van 1296. Daarin is sprake van een privilege, dat bisschop Otto aan de stad zou hebben gegeven. Deze Otto zal waarschijnlijk Otto van Holland zijn geweest, die van 1233 ,.., 1249 elect en bisschop van Utrecht was. In 1249 bezat Oldenzaal dus in elk geval reeds stáds,.., recht. -

The Path to the FAIR HANSA FAIR for More Than 600 Years, a Unique Network HANSA of Merchants Existed in Northern Europe
The path to the FAIR HANSA FAIR For more than 600 years, a unique network HANSA of merchants existed in Northern Europe. The cooperation of this consortium of merchants for the promotion of their foreign trade gave rise to an association of cities, to which around 200 coastal and inland cities belonged in the course of time. The Hanseatic League in the Middle Ages These cities were located in an area that today encom- passes seven European countries: from the Dutch Zui- derzee in the west to Baltic Estonia in the east, and from Sweden‘s Visby / Gotland in the north to the Cologne- Erfurt-Wroclaw-Krakow perimeter in the south. From this base, the Hanseatic traders developed a strong economic in uence, which during the 16th century extended from Portugal to Russia and from Scandinavia to Italy, an area that now includes 20 European states. Honest merchants – Fair Trade? Merchants, who often shared family ties to each other, were not always fair to producers and craftsmen. There is ample evidence of routine fraud and young traders in far- ung posts who led dissolute lives. It has also been proven that slave labor was used. ̇ ̆ Trading was conducted with goods that were typically regional, and sometimes with luxury goods: for example, wax and furs from Novgorod, cloth, silver, metal goods, salt, herrings and Chronology: grain from Hanseatic cities such as Lübeck, Münster or Dortmund 12th–14th Century - “Kaufmannshanse”. Establishment of Hanseatic trading posts (Hanseatic kontors) with common privi- leges for Low German merchants 14th–17th Century - “Städtehanse”. Cooperation between the Hanseatic cit- ies to defend their trade privileges and Merchants from di erent cities in di erent enforce common interests, especially at countries formed convoys and partnerships. -

Download Scans
De iirthiev Overjjcsei Sainsom Alphen aan den Rijn DE ARCHIEVEN IN OVERIJSSEL Omslag: brief van de griffier van de Staten van Overijssel aan de drost van Twenthe over de verblijfplaats van het drostenarchief, 1623 (Rijksarchief in Overijssel, archief Landsklaring, nr. 5500). OVERZICHTEN VAN DE ARCHIEVEN EN VERZAMELINGEN IN DE OPENBARE ARCHIEFBEWAARPLAATSEN IN NEDERLAND uitgegeven onder auspiciën van de Vereniging van Archivarissen in Nederland redactie: L.M.Th.L. Hustinx F.C.J. Ketelaar H.J.H.A.G. Metselaars J.J. Temminck H. Uil DEEL VI DE ARCHIEVEN IN OVERIJSSEL DE ARCHIEVEN IN OVERIJSSEL samengesteld door H. de Beer, Caspar van Heel, W.A. Huijsmans en A.J. Mensema Samsom Uitgeverij bv, Alphen aan den Rijn, 1980 Dit overzicht is bijgewerkt tot 31 december 1979. Voor deze uitgave werd financiële steun verleend door het Ministerie van Cultuur, Recreatie en Maatschappelijk Werk. Copyright © 1980 Samsom Uitgeverij, The Netherlands. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording or otherwise, without the prior permission of Samsom Uitgeveri j . ISBN 90 14 03025 8 INHOUD Kaarten: gemeentelijke indeling, indeling van drostambten, richter- en schoutambten, marken en steden, waterschapsindeling XIV Woord vooraf XVII Inleiding XIX 0 Algemeen XIX 1 Archieven XIX 1.1 Archieven, archiefbewaarplaatsen, verzamelingen XIX 1.2 Openbaarheid en toegankelijkheid XX 2 Archiefvormende instellingen XXI 2.1 Gewestelijke besturen en provinciale instellingen en ambtenaren XXII 2.1.1 vóór 1528 XXII 2.1.2 1528-1578 XXII 2.1.3 1578-1798 XXII 2.1.4 1798-1813 XXIV 2.1.5 sinds 1813 XXVI 2.2 Plaatselijke instellingen XXVII 2.2.1 Plaatselijk bestuur en rechtspraak vóór 1811 XXVII 2.2.2 Plaatselijk bestuur sinds 1811. -
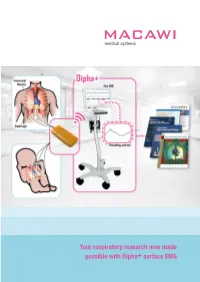
Your Respiratory Research Now Made Possible with Dipha+ Surface EMG Bland-Altman Plot Shows Asynchrony
Your respiratory research now made possible with Dipha+ surface EMG Bland-Altman plot shows asynchrony 1000,00 500,00 The Dipha+ 0 -500,00 -1000,00 Dipha+ enables scientific research in the respiratory field on -1500,00 patients ranging from preterm infants up to adults. It provides -2000,00 mean tE - tEsEMG (msec) 500,00 1000,00 1500,00 2000,00 2500,00 accurate, reliable and user-friendly surface EMG, sEMG, mean(msec) measurements of the diaphragm and intercostal muscles and data analysis. Dipha+ is typically used in the following areas: Detection of patient-ventilator asynchrony by using sEMG by J.Jurgens and J.L.C. Lokin at the (Adult) Intensive Care Unit, • Ventilation • Asthma AMC, Amsterdam. In a pilot study patient-ventilator asynchrony • Respiratory physiology • COPD in adult patients was analysed by combining measurements of • Anaesthesiology • Cystic Fibrosis the airway flow and sEMG of the diaphragm. “Good feasibility, repeatability and correlation of timing indices between sEMG signals and flow were found… Patient-ventilator asynchrony Some of the publications which are supported was detected in 28 of the 29 patients. This pilot study showing by MACAWI Dipha technology are: sEMG measurements can be reliably performed and may detect patient ventilator asynchrony...” Feasibility of a new cardio-respiratory monitor in preterm infants: Transcutaneous Electromyography of the Non invasive measurement of diaphragmatic activity after Diaphragm by J.V.S. Kraaijenga, G.J. Hutten, F.H.C. de Jongh, posterior brachial plexus block (PIPPA) by E.J.W. Maarsingh A.H. van Kaam at the Department of Neonatology, Emma et al. at Diving Medical Center, Royal Navy, Den Helder, Erasmus children’s hospital, AMC, Amsterdam. -

Beyond Isolation: Understanding Past Human-Population Variability in The
Archaeol Anthropol Sci https://doi.org/10.1007/s12520-017-0565-7 ORIGINAL PAPER Beyond isolation: understanding past human-population variability in the Dutch town of Oldenzaal through the origin of its inhabitants and its infrastructural connections L. M. Kootker1,2 & R. J. van Lanen3,4 & B. J. Groenewoudt3 & E. Altena5 & R. G. A. M. Panhuysen6,7 & E. Jansma3,4 & H. Kars2 & G. R. Davies1 Received: 30 May 2017 /Accepted: 8 November 2017 # The Author(s) 2017. This article is an open access publication Abstract This study presents a first attempt to assess the working hypothesis was that in the past a high degree of spa- mechanisms and potential controls behind past residential mo- tial connectivity of settlements must have been positively re- bility through the integration of isotopic data from human lated to a highly variable geographical origin of its inhabitants, inhumations and spatial infrastructural information pertaining the isotopic data from Oldenzaal indicate a population char- to the settlement containing these inhumations. Strontium acterized by a low variability in terms of their origin. This 87 86 18 ( Sr/ Sr) and oxygen (δ OPDB) isotope data are derived unexpected result may be caused by (a combination of) vari- from 200 (post)medieval individuals from the town of ous factors, related to (1) biases in the isotopic dataset, (2) Oldenzaal in the present-day Netherlands. Reconstructions interpretative limitations regarding the results of isotopic anal- of historical route networks show that Oldenzaal was well- yses and (3) the impact of broader socio-cultural factors that connected interregionally throughout the Middle Ages and cannot be traced through isotopic analyses, such as infrastruc- early-modern times (ca. -

Seaport - City Name & Code Tên & Mã Các C Ảng Bi Ển - Đị a Điểm
HANLOG LOGISTICS TRADING CO.,LTD No. 4B, Lane 49, Group 21, Tran Cung Street Nghia Tan Ward, Cau Giay Dist, Hanoi, Vietnam Tel: +84 24 2244 6555 Hotline: + 84 913 004 899 Email: [email protected] Website: www.hanlog.vn SEAPORT - CITY NAME & CODE TÊN & MÃ CÁC C ẢNG BI ỂN - ĐỊ A ĐIỂM Mã/Code Tên thành ph ố/City Mã qu ốc gia/Country Code Tên qu ốc gia/Country Name AFBIN BAMIAN AF Afganistan AFBST BOST AF Afganistan AFCCN CHAKCHARAN AF Afganistan AFDAZ DARWAZ AF Afganistan AFFBD FAIZABAD AF Afganistan AFFAH FARAH AF Afganistan AFGRG GARDEZ AF Afganistan AFGZI GHAZNI AF Afganistan AFHEA HERAT AF Afganistan AFJAA JALALABAD AF Afganistan AFKBL KABUL AF Afganistan AFKDH KANDAHAR AF Afganistan AFKHT KHOST AF Afganistan AFKWH KHWAHAN AF Afganistan AFUND KUNDUZ AF Afganistan AFKUR KURAN-O-MUNJAN AF Afganistan AFMMZ MAIMANA AF Afganistan AFMZR MAZAR-I-SHARIF AF Afganistan AFIMZ NIMROZ AF Afganistan AFZZZ OTHER AF Afganistan AFLQN QALA NAU AF Afganistan AFSBF SARDEH BAND AF Afganistan AFSGA SHEGHNAN AF Afganistan AFTQN TALUQAN AF Afganistan AFTII TIRINKOT AF Afganistan AFURN URGOON AF Afganistan AFURZ UROOZGAN AF Afganistan AFZAJ ZARANJ AF Afganistan ALDRZ DURRES (DURAZZO) AL Albania ALZZZ OTHER AL Albania ALSAR SARANDE AL Albania ALSHG SHENGJIN AL Albania ALTIA TIRANA AL Albania DZALG ALGER DZ Algeria DZAAE ANNABA (EX BONE) DZ Algeria DZAZW ARZEW DZ Algeria DZBJA BEJAIA (FORMERLY BOU DZ Algeria DZBSF BENISAF DZ Algeria DZCHE CHERCHELL DZ Algeria DZCOL COLLO DZ Algeria DZCZL CONSTANTINE DZ Algeria DZDEL DELLYS DZ Algeria DZDJI DJIDJELLI DZ Algeria