Analysis of Errors Introduced by Geographic Coordinate Systems on Weather Numeric Prediction Modeling
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Apparent Size of Celestial Objects
NATURE [April 7, 1870 daher wie schon fri.jher die Vor!esungen Uber die Warme, so of rectifying, we assume. :J'o me the Moon at an altit11de of auch jetzt die vorliegenden Vortrage Uber d~n Sc:hall unter 1~rer 45° is about (> i!lches in diameter ; when near the horizon, she is besonderen Aufsicht iibersetzen lasse~, und die :On1ckbogen e1µer about a foot. If I look through a telescope of small ruag11ifyjng genauen Durchsicht unterzogen, dam1t auch die deutsche J3ear power (say IO or 12 diameters), sQ as to leave a fair margin in beitung den englischen Werken ihres Freundes Tyndall nach the field, the Moon is still 6 inches in diameter, though her Form und Inhalt moglichst entsprache.-H. :fIEL!>iHOLTZ, G. visible area has really increased a hundred:fold. WIEDEMANN." . Can we go further than to say, as has often been said, that aH Prof. Tyndall's work, his account of Helmhqltz's Theory of magnitudi; is relative, and that nothing is great or small except Dissonance included, having passed through the hands of Helm by comparison? · · W. R. GROVE, holtz himself, not only without protest or correction, bnt with u5, Harley Street, April 4 the foregoing expression of opinion, it does not seem lihly that any serious dimag'e has been done.] · An After Pirm~. Jl;xperim1mt SUPPOSE in the experiment of an ellipsoid or spheroid, referred Apparent Size of Celestial Qpjecti:; to in my last letter, rolling between two parallel liorizontal ABOUT fifteen years ago I was looking at Venus through a planes, we were to scratch on the rolling body the two equal 40-inch telescope, Venus then being very near the Moon and similar and opposite closed curves (the polhods so-called), traced of a crescent form, the line across the middle or widest part upon it by the successive axes of instantaneou~ solutioll ; and of the crescent being about one-tenth of the planet's diameter. -

Shaded Elevation Map of Ohio
STATE OF OHIO DEPARTMENT OF NATURAL RESOURCES DIVISION OF GEOLOGICAL SURVEY Ted Strickland, Governor Sean D. Logan, Director Lawrence H. Wickstrom, Chief SHADED ELEVATION MAP OF OHIO 0 10 20 30 40 miles 0 10 20 30 40 kilometers SCALE 1:2,000,000 427-500500-600600-700700-800800-900900-10001000-11001100-12001200-13001300-14001400-1500>1500 Land elevation in feet Lake Erie water depth in feet 0-6 7-12 13-18 19-24 25-30 31-36 37-42 43-48 49-54 55-60 61-66 67-84 SHADED ELEVATION MAP This map depicts the topographic relief of Ohio’s landscape using color lier impeded the southward-advancing glaciers, causing them to split into to represent elevation intervals. The colorized topography has been digi- two lobes, the Miami Lobe on the west and the Scioto Lobe on the east. tally shaded from the northwest slightly above the horizon to give the ap- Ridges of thick accumulations of glacial material, called moraines, drape pearance of a three-dimensional surface. The map is based on elevation around the outlier and are distinct features on the map. Some moraines in data from the U.S. Geological Survey’s National Elevation Dataset; the Ohio are more than 200 miles long. Two other glacial lobes, the Killbuck grid spacing for the data is 30 meters. Lake Erie water depths are derived and the Grand River Lobes, are present in the northern and northeastern from National Oceanic and Atmospheric Administration data. This digi- portions of the state. tally derived map shows details of Ohio’s topography unlike any map of 4 Eastern Continental Divide—A continental drainage divide extends the past. -

Meyers Height 1
University of Connecticut DigitalCommons@UConn Peer-reviewed Articles 12-1-2004 What Does Height Really Mean? Part I: Introduction Thomas H. Meyer University of Connecticut, [email protected] Daniel R. Roman National Geodetic Survey David B. Zilkoski National Geodetic Survey Follow this and additional works at: http://digitalcommons.uconn.edu/thmeyer_articles Recommended Citation Meyer, Thomas H.; Roman, Daniel R.; and Zilkoski, David B., "What Does Height Really Mean? Part I: Introduction" (2004). Peer- reviewed Articles. Paper 2. http://digitalcommons.uconn.edu/thmeyer_articles/2 This Article is brought to you for free and open access by DigitalCommons@UConn. It has been accepted for inclusion in Peer-reviewed Articles by an authorized administrator of DigitalCommons@UConn. For more information, please contact [email protected]. Land Information Science What does height really mean? Part I: Introduction Thomas H. Meyer, Daniel R. Roman, David B. Zilkoski ABSTRACT: This is the first paper in a four-part series considering the fundamental question, “what does the word height really mean?” National Geodetic Survey (NGS) is embarking on a height mod- ernization program in which, in the future, it will not be necessary for NGS to create new or maintain old orthometric height benchmarks. In their stead, NGS will publish measured ellipsoid heights and computed Helmert orthometric heights for survey markers. Consequently, practicing surveyors will soon be confronted with coping with these changes and the differences between these types of height. Indeed, although “height’” is a commonly used word, an exact definition of it can be difficult to find. These articles will explore the various meanings of height as used in surveying and geodesy and pres- ent a precise definition that is based on the physics of gravitational potential, along with current best practices for using survey-grade GPS equipment for height measurement. -

Introduction to Astronomy from Darkness to Blazing Glory
Introduction to Astronomy From Darkness to Blazing Glory Published by JAS Educational Publications Copyright Pending 2010 JAS Educational Publications All rights reserved. Including the right of reproduction in whole or in part in any form. Second Edition Author: Jeffrey Wright Scott Photographs and Diagrams: Credit NASA, Jet Propulsion Laboratory, USGS, NOAA, Aames Research Center JAS Educational Publications 2601 Oakdale Road, H2 P.O. Box 197 Modesto California 95355 1-888-586-6252 Website: http://.Introastro.com Printing by Minuteman Press, Berkley, California ISBN 978-0-9827200-0-4 1 Introduction to Astronomy From Darkness to Blazing Glory The moon Titan is in the forefront with the moon Tethys behind it. These are two of many of Saturn’s moons Credit: Cassini Imaging Team, ISS, JPL, ESA, NASA 2 Introduction to Astronomy Contents in Brief Chapter 1: Astronomy Basics: Pages 1 – 6 Workbook Pages 1 - 2 Chapter 2: Time: Pages 7 - 10 Workbook Pages 3 - 4 Chapter 3: Solar System Overview: Pages 11 - 14 Workbook Pages 5 - 8 Chapter 4: Our Sun: Pages 15 - 20 Workbook Pages 9 - 16 Chapter 5: The Terrestrial Planets: Page 21 - 39 Workbook Pages 17 - 36 Mercury: Pages 22 - 23 Venus: Pages 24 - 25 Earth: Pages 25 - 34 Mars: Pages 34 - 39 Chapter 6: Outer, Dwarf and Exoplanets Pages: 41-54 Workbook Pages 37 - 48 Jupiter: Pages 41 - 42 Saturn: Pages 42 - 44 Uranus: Pages 44 - 45 Neptune: Pages 45 - 46 Dwarf Planets, Plutoids and Exoplanets: Pages 47 -54 3 Chapter 7: The Moons: Pages: 55 - 66 Workbook Pages 49 - 56 Chapter 8: Rocks and Ice: -

Geographical Influences on Climate Teacher Guide
Geographical Influences on Climate Teacher Guide Lesson Overview: Students will compare the climatograms for different locations around the United States to observe patterns in temperature and precipitation. They will describe geographical features near those locations, and compare graphs to find patterns in the effect of mountains, oceans, elevation, latitude, etc. on temperature and precipitation. Then, students will research temperature and precipitation patterns at various locations around the world using the MY NASA DATA Live Access Server and other sources, and use the information to create their own climatogram. Expected time to complete lesson: One 45 minute period to compare given climatograms, one to two 45 minute periods to research another location and create their own climatogram. To lessen the time needed, you can provide students data rather than having them find it themselves (to focus on graphing and analysis), or give them the template to create a climatogram (to focus on the analysis and description), or give them the assignment for homework. See GPM Geographical Influences on Climate – Climatogram Template and Data for these options. Learning Objectives: - Students will brainstorm geographic features, consider how they might affect temperature and precipitation, and discuss the difference between weather and climate. - Students will examine data about a location and calculate averages to compare with other locations to determine the effect of geographic features on temperature and precipitation. - Students will research the climate patterns of a location and create a climatogram and description of what factors affect the climate at that location. National Standards: ESS2.D: Weather and climate are influenced by interactions involving sunlight, the ocean, the atmosphere, ice, landforms, and living things. -

Geodetic Position Computations
GEODETIC POSITION COMPUTATIONS E. J. KRAKIWSKY D. B. THOMSON February 1974 TECHNICALLECTURE NOTES REPORT NO.NO. 21739 PREFACE In order to make our extensive series of lecture notes more readily available, we have scanned the old master copies and produced electronic versions in Portable Document Format. The quality of the images varies depending on the quality of the originals. The images have not been converted to searchable text. GEODETIC POSITION COMPUTATIONS E.J. Krakiwsky D.B. Thomson Department of Geodesy and Geomatics Engineering University of New Brunswick P.O. Box 4400 Fredericton. N .B. Canada E3B5A3 February 197 4 Latest Reprinting December 1995 PREFACE The purpose of these notes is to give the theory and use of some methods of computing the geodetic positions of points on a reference ellipsoid and on the terrain. Justification for the first three sections o{ these lecture notes, which are concerned with the classical problem of "cCDputation of geodetic positions on the surface of an ellipsoid" is not easy to come by. It can onl.y be stated that the attempt has been to produce a self contained package , cont8.i.ning the complete development of same representative methods that exist in the literature. The last section is an introduction to three dimensional computation methods , and is offered as an alternative to the classical approach. Several problems, and their respective solutions, are presented. The approach t~en herein is to perform complete derivations, thus stqing awrq f'rcm the practice of giving a list of for11111lae to use in the solution of' a problem. -
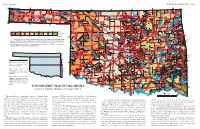
TOPOGRAPHIC MAP of OKLAHOMA Kenneth S
Page 2, Topographic EDUCATIONAL PUBLICATION 9: 2008 Contour lines (in feet) are generalized from U.S. Geological Survey topographic maps (scale, 1:250,000). Principal meridians and base lines (dotted black lines) are references for subdividing land into sections, townships, and ranges. Spot elevations ( feet) are given for select geographic features from detailed topographic maps (scale, 1:24,000). The geographic center of Oklahoma is just north of Oklahoma City. Dimensions of Oklahoma Distances: shown in miles (and kilometers), calculated by Myers and Vosburg (1964). Area: 69,919 square miles (181,090 square kilometers), or 44,748,000 acres (18,109,000 hectares). Geographic Center of Okla- homa: the point, just north of Oklahoma City, where you could “balance” the State, if it were completely flat (see topographic map). TOPOGRAPHIC MAP OF OKLAHOMA Kenneth S. Johnson, Oklahoma Geological Survey This map shows the topographic features of Oklahoma using tain ranges (Wichita, Arbuckle, and Ouachita) occur in southern contour lines, or lines of equal elevation above sea level. The high- Oklahoma, although mountainous and hilly areas exist in other parts est elevation (4,973 ft) in Oklahoma is on Black Mesa, in the north- of the State. The map on page 8 shows the geomorphic provinces The Ouachita (pronounced “Wa-she-tah”) Mountains in south- 2,568 ft, rising about 2,000 ft above the surrounding plains. The west corner of the Panhandle; the lowest elevation (287 ft) is where of Oklahoma and describes many of the geographic features men- eastern Oklahoma and western Arkansas is a curved belt of forested largest mountainous area in the region is the Sans Bois Mountains, Little River flows into Arkansas, near the southeast corner of the tioned below. -

Datums in Texas NGS: Welcome to Geodesy
Datums in Texas NGS: Welcome to Geodesy Geodesy is the science of measuring and monitoring the size and shape of the Earth and the location of points on its surface. NOAA's National Geodetic Survey (NGS) is responsible for the development and maintenance of a national geodetic data system that is used for navigation, communication systems, and mapping and charting. ln this subject, you will find three sections devoted to learning about geodesy: an online tutorial, an educational roadmap to resources, and formal lesson plans. The Geodesy Tutorial is an overview of the history, essential elements, and modern methods of geodesy. The tutorial is content rich and easy to understand. lt is made up of 10 chapters or pages (plus a reference page) that can be read in sequence by clicking on the arrows at the top or bottom of each chapter page. The tutorial includes many illustrations and interactive graphics to visually enhance the text. The Roadmap to Resources complements the information in the tutorial. The roadmap directs you to specific geodetic data offered by NOS and NOAA. The Lesson Plans integrate information presented in the tutorial with data offerings from the roadmap. These lesson plans have been developed for students in grades 9-12 and focus on the importance of geodesy and its practical application, including what a datum is, how a datum of reference points may be used to describe a location, and how geodesy is used to measure movement in the Earth's crust from seismic activity. Members of a 1922 geodetic suruey expedition. Until recent advances in satellite technology, namely the creation of the Global Positioning Sysfem (GPS), geodetic surveying was an arduous fask besf suited to individuals with strong constitutions, and a sense of adventure. -

Models for Earth and Maps
Earth Models and Maps James R. Clynch, Naval Postgraduate School, 2002 I. Earth Models Maps are just a model of the world, or a small part of it. This is true if the model is a globe of the entire world, a paper chart of a harbor or a digital database of streets in San Francisco. A model of the earth is needed to convert measurements made on the curved earth to maps or databases. Each model has advantages and disadvantages. Each is usually in error at some level of accuracy. Some of these error are due to the nature of the model, not the measurements used to make the model. Three are three common models of the earth, the spherical (or globe) model, the ellipsoidal model, and the real earth model. The spherical model is the form encountered in elementary discussions. It is quite good for some approximations. The world is approximately a sphere. The sphere is the shape that minimizes the potential energy of the gravitational attraction of all the little mass elements for each other. The direction of gravity is toward the center of the earth. This is how we define down. It is the direction that a string takes when a weight is at one end - that is a plumb bob. A spirit level will define the horizontal which is perpendicular to up-down. The ellipsoidal model is a better representation of the earth because the earth rotates. This generates other forces on the mass elements and distorts the shape. The minimum energy form is now an ellipse rotated about the polar axis. -

Using a Surveyor's Level to Generate a Topographical
Using a Surveyor’s Level to Generate a Topographical Map This application note describes the process of using a surveyor's level for generating a topography (topo) map. The site survey described below uses San Francisco's Yerba Buena Gardens as a site for recording relative elevations over a specific area. With these relative elevations organized into a grid, a topographical map can be created. Equipment: (most available from Tool Lending Library): Surveyor's Level Level Tripod Leveling Rod Compass 100' Tape Measure Notebook and Pencil Procedure: Step 1: Find a Reference Point (Benchmark Elevation) Step 2: Set up the Surveyor's Level Step 3: Reading the Leveling Rod Step 4: Taking Readings Step 5: Make a Grid Over the Chosen Plot Step 6: Making Sense of the Collected Data Step 7: Drawing Topography Lines Figure 1: Surveyor’s level Step 1: Find a Reference Point (Benchmark Elevation) 1. Establish a reference point, also known as the benchmark elevation. A list of official benchmark elevations in San Francisco is available from the Bureau of Street Use and Mapping. (located at 875 Stevenson Street, Room 460 /// San Francisco, CA. 94103 /// 415.554.5810). The nearest benchmark to the plot is the intersection of 4th and Mission Street. (Figure 2). Using a Surveyor’s Level to Generate a Topography Map Page 1 of 8 Copyright© Pacific Gas and Electric Company, all rights reserved www.pge.com/pec Figure 2: Benchmark descriptions as printed by the SF Bureau of Street Use and Mapping. The benchmark on the list in Figure 2 is a fire hydrant with the word "OPEN" on top. -

TIDAL THEORY By: Paul O’Hargan
TIDAL THEORY By: Paul O’Hargan (1Tidaltheory.doc, revision – 12/14/2000) INTRODUCTION The word "tides" is a generic term used to define the alternating rise and fall in sea level with respect to the land, produced, in part, by the gravitational attraction of the moon and sun. There are additional nonastronomical factors influencing local heights and times of tides such as configuration of the coastline, depth of the water, ocean-floor topography, and other hydrographic and meteorological influences. Knowledge of these heights and times is important in practical applications such as navigation, harbor construction, tidal datums for hydrography and for mean high water line survey procedures, the determination of base lines for fixing offshore territorial limits and for tide predictions. ORIGIN OF ASTRONOMICAL TIDE RAISING FORCES At the surface of the earth, the earth's force of gravitational attraction acts in a direction toward its center, and thus holds the ocean waters confined to this surface. However, the gravitational forces of the moon and sun also act externally upon the earth's ocean waters. These external forces are exerted as tide producing forces, called tractive forces. To all outward appearances, the moon revolves around the earth, but in actuality, the moon and earth revolve together around their common center of mass called the barycenter. The two astronomical bodies are held together by gravitational attraction, but are simultaneously kept apart by an equal and opposite centrifugal force. At the earth's surface an imbalance between these two forces results in the fact that there exists, on the side of the earth turned toward the moon, a net tide producing force which acts in the direction of the moon. -

Solar System KEY.Pdf
Solar System 1. The diagram below represents a simple geocentric model. Which object is represented by the letter X? A) Earth B) Sun C) Moon D) Polaris 2. Which object orbits Earth in both the Earth-centered (geocentric) and Sun-centered (heliocentric) models of our solar system? A) the Moon B) the Sun C) Venus D) Polaris 3. In which type of model are the Sun, other stars, and the Moon in orbit around the Earth? A) heliocentric model B) tetrahedral model C) concentric model D) geocentric model 4. The diagram below shows one model of a portion of the universe. What type of model does the diagram best demonstrate? A) a heliocentric model, in which celestial objects orbit Earth B) a heliocentric model, in which celestial objects orbit the Sun C) a geocentric model, in which celestial objects orbit Earth D) a geocentric model, in which celestial objects orbit the Sun 5. Which diagram represents a geocentric model? [Key: E = Earth, P = Planet, S = Sun] A) B) C) D) 6. Which statement best describes the geocentric model of our solar system? A) The Earth is located at the center of the model. B) All planets revolve around the Sun. C) The Sun is located at the center of the model. D) All planets except the Earth revolve around the Sun. 7. Which apparent motion can be explained by a geocentric model? A) deflection of the wind B) curved path of projectiles C) motion of a Foucault pendulum D) the sun's path through the sky 8. In the geocentric model (the Earth at the center of the universe), which motion would occur? A) The Earth would revolve around the Sun.