Thirteen Ways to Look at the Correlation Coefficient
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Statistics on Spotlight: World Statistics Day 2015
Statistics on Spotlight: World Statistics Day 2015 Shahjahan Khan Professor of Statistics School of Agricultural, Computational and Environmental Sciences University of Southern Queensland, Toowoomba, Queensland, AUSTRALIA Founding Chief Editor, Journal of Applied Probability and Statistics (JAPS), USA Email: [email protected] Abstract In the age of evidence based decision making and data science, statistics has become an integral part of almost all spheres of modern life. It is being increasingly applied for both private and public benefits including business and trade as well as various public sectors, not to mention its crucial role in research and innovative technologies. No modern government could conduct its normal functions and deliver its services and implement its development agenda without relying on good quality statistics. The key role of statistics is more visible and engraved in the planning and development of every successful nation state. In fact, the use of statistics is not only national but also regional, international and transnational for organisations and agencies that are driving social, economic, environmental, health, poverty elimination, education and other agendas for planned development. Starting from stocktaking of the state of the health of various sectors of the economy of any nation/region to setting development goals, assessment of progress, monitoring programs and undertaking follow-up initiatives depend heavily on relevant statistics. Only statistical methods are capable of determining indicators, comparing them, and help identify the ways to ensure balanced and equitable development. 1 Introduction The goals of the celebration of World Statistics Day 2015 is to highlight the fact that official statistics help decision makers develop informed policies that impact millions of people. -

04 – Everything You Want to Know About Correlation but Were
EVERYTHING YOU WANT TO KNOW ABOUT CORRELATION BUT WERE AFRAID TO ASK F R E D K U O 1 MOTIVATION • Correlation as a source of confusion • Some of the confusion may arise from the literary use of the word to convey dependence as most people use “correlation” and “dependence” interchangeably • The word “correlation” is ubiquitous in cost/schedule risk analysis and yet there are a lot of misconception about it. • A better understanding of the meaning and derivation of correlation coefficient, and what it truly measures is beneficial for cost/schedule analysts. • Many times “true” correlation is not obtainable, as will be demonstrated in this presentation, what should the risk analyst do? • Is there any other measures of dependence other than correlation? • Concordance and Discordance • Co-monotonicity and Counter-monotonicity • Conditional Correlation etc. 2 CONTENTS • What is Correlation? • Correlation and dependence • Some examples • Defining and Estimating Correlation • How many data points for an accurate calculation? • The use and misuse of correlation • Some example • Correlation and Cost Estimate • How does correlation affect cost estimates? • Portfolio effect? • Correlation and Schedule Risk • How correlation affect schedule risks? • How Shall We Go From Here? • Some ideas for risk analysis 3 POPULARITY AND SHORTCOMINGS OF CORRELATION • Why Correlation Is Popular? • Correlation is a natural measure of dependence for a Multivariate Normal Distribution (MVN) and the so-called elliptical family of distributions • It is easy to calculate analytically; we only need to calculate covariance and variance to get correlation • Correlation and covariance are easy to manipulate under linear operations • Correlation Shortcomings • Variances of R.V. -

11. Correlation and Linear Regression
11. Correlation and linear regression The goal in this chapter is to introduce correlation and linear regression. These are the standard tools that statisticians rely on when analysing the relationship between continuous predictors and continuous outcomes. 11.1 Correlations In this section we’ll talk about how to describe the relationships between variables in the data. To do that, we want to talk mostly about the correlation between variables. But first, we need some data. 11.1.1 The data Table 11.1: Descriptive statistics for the parenthood data. variable min max mean median std. dev IQR Dan’s grumpiness 41 91 63.71 62 10.05 14 Dan’s hours slept 4.84 9.00 6.97 7.03 1.02 1.45 Dan’s son’s hours slept 3.25 12.07 8.05 7.95 2.07 3.21 ............................................................................................ Let’s turn to a topic close to every parent’s heart: sleep. The data set we’ll use is fictitious, but based on real events. Suppose I’m curious to find out how much my infant son’s sleeping habits affect my mood. Let’s say that I can rate my grumpiness very precisely, on a scale from 0 (not at all grumpy) to 100 (grumpy as a very, very grumpy old man or woman). And lets also assume that I’ve been measuring my grumpiness, my sleeping patterns and my son’s sleeping patterns for - 251 - quite some time now. Let’s say, for 100 days. And, being a nerd, I’ve saved the data as a file called parenthood.csv. -

Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10
International Journal of Environmental Research and Public Health Article Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10 Rudy de Barros Ahrens 1,*, Luciana da Silva Lirani 2 and Antonio Carlos de Francisco 3 1 Department of Business, Faculty Sagrada Família (FASF), Ponta Grossa, PR 84010-760, Brazil 2 Department of Health Sciences Center, State University Northern of Paraná (UENP), Jacarezinho, PR 86400-000, Brazil; [email protected] 3 Department of Industrial Engineering and Post-Graduation in Production Engineering, Federal University of Technology—Paraná (UTFPR), Ponta Grossa, PR 84017-220, Brazil; [email protected] * Correspondence: [email protected] Received: 1 September 2020; Accepted: 29 September 2020; Published: 9 October 2020 Abstract: The purpose of this study was to validate the construct and reliability of an instrument to assess the work environment as a single tool based on quality of life (QL), quality of work life (QWL), and organizational climate (OC). The methodology tested the construct validity through Exploratory Factor Analysis (EFA) and reliability through Cronbach’s alpha. The EFA returned a Kaiser–Meyer–Olkin (KMO) value of 0.917; which demonstrated that the data were adequate for the factor analysis; and a significant Bartlett’s test of sphericity (χ2 = 7465.349; Df = 1225; p 0.000). ≤ After the EFA; the varimax rotation method was employed for a factor through commonality analysis; reducing the 14 initial factors to 10. Only question 30 presented commonality lower than 0.5; and the other questions returned values higher than 0.5 in the commonality analysis. Regarding the reliability of the instrument; all of the questions presented reliability as the values varied between 0.953 and 0.956. -
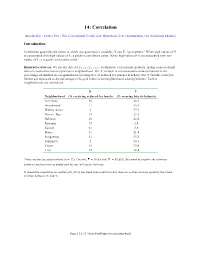
14: Correlation
14: Correlation Introduction | Scatter Plot | The Correlational Coefficient | Hypothesis Test | Assumptions | An Additional Example Introduction Correlation quantifies the extent to which two quantitative variables, X and Y, “go together.” When high values of X are associated with high values of Y, a positive correlation exists. When high values of X are associated with low values of Y, a negative correlation exists. Illustrative data set. We use the data set bicycle.sav to illustrate correlational methods. In this cross-sectional data set, each observation represents a neighborhood. The X variable is socioeconomic status measured as the percentage of children in a neighborhood receiving free or reduced-fee lunches at school. The Y variable is bicycle helmet use measured as the percentage of bicycle riders in the neighborhood wearing helmets. Twelve neighborhoods are considered: X Y Neighborhood (% receiving reduced-fee lunch) (% wearing bicycle helmets) Fair Oaks 50 22.1 Strandwood 11 35.9 Walnut Acres 2 57.9 Discov. Bay 19 22.2 Belshaw 26 42.4 Kennedy 73 5.8 Cassell 81 3.6 Miner 51 21.4 Sedgewick 11 55.2 Sakamoto 2 33.3 Toyon 19 32.4 Lietz 25 38.4 Three are twelve observations (n = 12). Overall, = 30.83 and = 30.883. We want to explore the relation between socioeconomic status and the use of bicycle helmets. It should be noted that an outlier (84, 46.6) has been removed from this data set so that we may quantify the linear relation between X and Y. Page 14.1 (C:\data\StatPrimer\correlation.wpd) Scatter Plot The first step is create a scatter plot of the data. -

CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (Moderately Hard)Or
5 COMPUTING CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (moderately hard)or WHAT YOU WILLpost, LEARN IN THIS CHAPTER • Understanding what correlations are and how they work • Computing a simple correlation coefficient • Interpretingcopy, the value of the correlation coefficient • Understanding what other types of correlations exist and when they notshould be used Do WHAT ARE CORRELATIONS ALL ABOUT? Measures of central tendency and measures of variability are not the only descrip- tive statistics that we are interested in using to get a picture of what a set of scores 76 Copyright ©2020 by SAGE Publications, Inc. This work may not be reproduced or distributed in any form or by any means without express written permission of the publisher. Chapter 5 ■ Computing Correlation Coefficients 77 looks like. You have already learned that knowing the values of the one most repre- sentative score (central tendency) and a measure of spread or dispersion (variability) is critical for describing the characteristics of a distribution. However, sometimes we are as interested in the relationship between variables—or, to be more precise, how the value of one variable changes when the value of another variable changes. The way we express this interest is through the computation of a simple correlation coefficient. For example, what’s the relationship between age and strength? Income and years of education? Memory skills and amount of drug use? Your political attitudes and the attitudes of your parents? A correlation coefficient is a numerical index that reflects the relationship or asso- ciation between two variables. The value of this descriptive statistic ranges between −1.00 and +1.00. -

Correlation of Salivary Immunoglobulin a Against Lipopolysaccharide of Porphyromonas Gingivalis with Clinical Periodontal Parameters
Correlation of salivary immunoglobulin A against lipopolysaccharide of Porphyromonas gingivalis with clinical periodontal parameters Pushpa S. Pudakalkatti, Abhinav S. Baheti Abstract Background: A major challenge in clinical periodontics is to find a reliable molecular marker of periodontal tissue destruction. Aim: The aim of the present study was to assess, whether any correlation exists between salivary immunoglobulin A (IgA) level against lipopolysaccharide of Porphyromonas gingivalis and clinical periodontal parameters (probing depth and clinical attachment loss). Materials and Methods: Totally, 30 patients with chronic periodontitis were included for the study based on clinical examination. Unstimulated saliva was collected from each study subject. Probing depth and clinical attachment loss were recorded in all selected subjects using University of North Carolina‑15 periodontal probe. Extraction and purification of lipopolysaccharide were done from the standard strain of P. gingivalis (ATCC 33277). Enzyme linked immunosorbent assay (ELISA) was used to detect the level of IgA antibodies against lipopolysaccharide of P. gingivalis in the saliva of each subject by coating wells of ELISA kit with extracted lipopolysaccharide antigen. Statistical Analysis: The correlation between salivary IgA and clinical periodontal parameters was checked using Karl Pearson’s correlation coefficient method and regression analysis. Results: The significant correlation was observed between salivary IgA level and clinical periodontal parameters in chronic -

Eight Things You Need to Know About Interpreting Correlations
Research Skills One, Correlation interpretation, Graham Hole v.1.0. Page 1 Eight things you need to know about interpreting correlations: A correlation coefficient is a single number that represents the degree of association between two sets of measurements. It ranges from +1 (perfect positive correlation) through 0 (no correlation at all) to -1 (perfect negative correlation). Correlations are easy to calculate, but their interpretation is fraught with difficulties because the apparent size of the correlation can be affected by so many different things. The following are some of the issues that you need to take into account when interpreting the results of a correlation test. 1. Correlation does not imply causality: This is the single most important thing to remember about correlations. If there is a strong correlation between two variables, it's easy to jump to the conclusion that one of the variables causes the change in the other. However this is not a valid conclusion. If you have two variables, X and Y, it might be that X causes Y; that Y causes X; or that a third factor, Z (or even a whole set of other factors) gives rise to the changes in both X and Y. For example, suppose there is a correlation between how many slices of pizza I eat (variable X), and how happy I am (variable Y). It might be that X causes Y - so that the more pizza slices I eat, the happier I become. But it might equally well be that Y causes X - the happier I am, the more pizza I eat. -

Chapter 11 -- Correlation
Contents 11 Association Between Variables 795 11.4 Correlation . 795 11.4.1 Introduction . 795 11.4.2 Correlation Coe±cient . 796 11.4.3 Pearson's r . 800 11.4.4 Test of Signi¯cance for r . 810 11.4.5 Correlation and Causation . 813 11.4.6 Spearman's rho . 819 11.4.7 Size of r for Various Types of Data . 828 794 Chapter 11 Association Between Variables 11.4 Correlation 11.4.1 Introduction The measures of association examined so far in this chapter are useful for describing the nature of association between two variables which are mea- sured at no more than the nominal scale of measurement. All of these measures, Á, C, Cramer's xV and ¸, can also be used to describe association between variables that are measured at the ordinal, interval or ratio level of measurement. But where variables are measured at these higher levels, it is preferable to employ measures of association which use the information contained in these higher levels of measurement. These higher level scales either rank values of the variable, or permit the researcher to measure the distance between values of the variable. The association between rankings of two variables, or the association of distances between values of the variable provides a more detailed idea of the nature of association between variables than do the measures examined so far in this chapter. While there are many measures of association for variables which are measured at the ordinal or higher level of measurement, correlation is the most commonly used approach. -

D 27 April 1936 Summary. Karl Pearson Was Founder of The
Karl PEARSON1 b. 27 March 1857 - d 27 April 1936 Summary. Karl Pearson was Founder of the Biometric School. He made prolific contributions to statistics, eugenics and to the scientific method. Stimulated by the applications of W.F.R. Weldon and F. Galton he laid the foundations of much of modern mathematical statistics. Founder of biometrics, Karl Pearson was one of the principal architects of the modern theory of mathematical statistics. He was a polymath whose interests ranged from astronomy, mechanics, meteorology and physics to the biological sciences in particular (including anthropology, eugenics, evolution- ary biology, heredity and medicine). In addition to these scientific pursuits, he undertook the study of German folklore and literature, the history of the Reformation and German humanists (especially Martin Luther). Pear- son’s writings were prodigious: he published more than 650 papers in his lifetime, of which 400 are statistical. Over a period of 28 years, he founded and edited 6 journals and was a co-founder (along with Weldon and Galton) of the journal Biometrika. University College London houses the main set of Pearson’s collected papers which consist of 235 boxes containing family papers, scientific manuscripts and 16,000 letters. Largely owing to his interests in evolutionary biology, Pearson created, al- most single-handedly, the modern theory of statistics in his Biometric School at University College London from 1892 to 1903 (which was practised in the Drapers’ Biometric Laboratory from 1903-1933). These developments were underpinned by Charles Darwin’s ideas of biological variation and ‘sta- tistical’ populations of species - arising from the impetus of statistical and experimental work of his colleague and closest friend, the Darwinian zoolo- gist, W.F.R. -

Alternatives to Pearson's and Spearman's Correlation Coefficients
Alternatives To Pearson’s and Spearman’s Correlation Coefficients Florentin Smarandache Chair of Math & Sciences Department University of New Mexico Gallup, NM 87301, USA Abstract. This article presents several alternatives to Pearson’s correlation coefficient and many examples. In the samples where the rank in a discrete variable counts more than the variable values, the mixture of Pearson’s and Spearman’s gives a better result. Introduction Let’s consider a bivariate sample, which consists of n ≥ 2 pairs (x,y). We denote these pairs by: (x1, y1), (x2, y2), … , (xn,yn), where xi = the value of x for the i-th observation, and yi = the value of y for the i-th observation, for any 1 < i < n. We can construct a scatter plot in order to detect any relationship between variables x and y, drawing a horizontal x-axis and a vertical y-axis, and plotting points of coordinates (xi, yi) for all i ∈{1, 2, …, n}. We use the standard statistics notations, mostly used in regression analysis: n n n ∑ x = ∑ xi , ∑∑y = yi , ∑∑xyxy= ()ii , i=1 i=1 i=1 n n 2 2 2 2 ∑ x = ∑ xi , ∑ y = ∑ yi , (1) i=1 i=1 n ∑ xi X = i=1 = the mean of sample variable x, n n ∑ yi Y = i=1 = the mean of sample variable y. n Let’s introduce a notation for the median: XM = the median of sample variable x, (2) YM = the median of sample variable y. Correlation Coefficients. Correlation coefficient of variables x and y shows how strongly the values of these variables are related to one another. -

Generalized Correlations and Kernel Causality Using R Package Generalcorr
Generalized Correlations and Kernel Causality Using R Package generalCorr Hrishikesh D. Vinod* October 3, 2017 Abstract Karl Pearson developed the correlation coefficient r(X,Y) in 1890's. Vinod (2014) develops new generalized correlation coefficients so that when r∗(Y X) > r∗(X Y) then X is the \kernel cause" of Y. Vinod (2015a) arguesj that kernelj causality amounts to model selection be- tween two kernel regressions, E(Y X) = g1(X) and E(X Y) = g2(Y) and reports simulations favoring kernelj causality. An Rj software pack- age called `generalCorr' (at www.r-project.org) computes general- ized correlations, partial correlations and plausible causal paths. This paper describes various R functions in the package, using examples to describe them. We are proposing an alternative quantification to extensive causality apparatus of Pearl (2010) and additive-noise type methods in Mooij et al. (2014), who seem to offer no R implementa- tions. My methods applied to certain public benchmark data report a 70-75% success rate. We also describe how to use the package to assess endogeneity of regressors. Keywords: generalized measure of correlation, non-parametric regres- sion, partial correlation, observational data, endogeneity. *Vinod: Professor of Economics, Fordham University, Bronx, New York, USA 104 58. E-mail: [email protected]. A version of this paper was presented at American Statistical Association's Conference on Statistical Practice (CSP) on Feb. 19, 2016, in San Diego, California, and also at the 11-th Greater New York Metro Area Econometrics Colloquium, Johns Hopkins University, Baltimore, Maryland, on March 5, 2016. I thank Dr Pierre Marie Windal of Paris for pointing out an error in partial correlation coefficients.