11. Correlation and Linear Regression
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
![Anomalous Perception in a Ganzfeld Condition - a Meta-Analysis of More Than 40 Years Investigation [Version 1; Peer Review: Awaiting Peer Review]](https://docslib.b-cdn.net/cover/5459/anomalous-perception-in-a-ganzfeld-condition-a-meta-analysis-of-more-than-40-years-investigation-version-1-peer-review-awaiting-peer-review-5459.webp)
Anomalous Perception in a Ganzfeld Condition - a Meta-Analysis of More Than 40 Years Investigation [Version 1; Peer Review: Awaiting Peer Review]
F1000Research 2021, 10:234 Last updated: 08 SEP 2021 RESEARCH ARTICLE Stage 2 Registered Report: Anomalous perception in a Ganzfeld condition - A meta-analysis of more than 40 years investigation [version 1; peer review: awaiting peer review] Patrizio E. Tressoldi 1, Lance Storm2 1Studium Patavinum, University of Padua, Padova, Italy 2School of Psychology, University of Adelaide, Adelaide, Australia v1 First published: 24 Mar 2021, 10:234 Open Peer Review https://doi.org/10.12688/f1000research.51746.1 Latest published: 24 Mar 2021, 10:234 https://doi.org/10.12688/f1000research.51746.1 Reviewer Status AWAITING PEER REVIEW Any reports and responses or comments on the Abstract article can be found at the end of the article. This meta-analysis is an investigation into anomalous perception (i.e., conscious identification of information without any conventional sensorial means). The technique used for eliciting an effect is the ganzfeld condition (a form of sensory homogenization that eliminates distracting peripheral noise). The database consists of studies published between January 1974 and December 2020 inclusive. The overall effect size estimated both with a frequentist and a Bayesian random-effect model, were in close agreement yielding an effect size of .088 (.04-.13). This result passed four publication bias tests and seems not contaminated by questionable research practices. Trend analysis carried out with a cumulative meta-analysis and a meta-regression model with Year of publication as covariate, did not indicate sign of decline of this effect size. The moderators analyses show that selected participants outcomes were almost three-times those obtained by non-selected participants and that tasks that simulate telepathic communication show a two- fold effect size with respect to tasks requiring the participants to guess a target. -

Dentist's Knowledge of Evidence-Based Dentistry and Digital Applications Resources in Saudi Arabia
PTB Reports Research Article Dentist’s Knowledge of Evidence-based Dentistry and Digital Applications Resources in Saudi Arabia Yousef Ahmed Alomi*, BSc. Pharm, MSc. Clin Pharm, BCPS, BCNSP, DiBA, CDE ABSTRACT Critical Care Clinical Pharmacists, TPN Objectives: Drug information resources provide clinicians with safer use of medications and play a Clinical Pharmacist, Freelancer Business vital role in improving drug safety. Evidence-based medicine (EBM) has become essential to medical Planner, Content Editor, and Data Analyst, Riyadh, SAUDI ARABIA. practice; however, EBM is still an emerging dentistry concept. Therefore, in this study, we aimed to Anwar Mouslim Alshammari, B.D.S explore dentists’ knowledge about evidence-based dentistry resources in Saudi Arabia. Methods: College of Destiney, Hail University, SAUDI This is a 4-month cross-sectional study conducted to analyze dentists’ knowledge about evidence- ARABIA. based dentistry resources in Saudi Arabia. We included dentists from interns to consultants and Hanin Sumaydan Saleam Aljohani, those across all dentistry specialties and located in Saudi Arabia. The survey collected demographic Ministry of Health, Riyadh, SAUDI ARABIA. information and knowledge of resources on dental drugs. The knowledge of evidence-based dental care and knowledge of dental drug information applications. The survey was validated through the Correspondence: revision of expert reviewers and pilot testing. Moreover, various reliability tests had been done with Dr. Yousef Ahmed Alomi, BSc. Pharm, the study. The data were collected through the Survey Monkey system and analyzed using Statistical MSc. Clin Pharm, BCPS, BCNSP, DiBA, CDE Critical Care Clinical Pharmacists, TPN Package of Social Sciences (SPSS) and Jeffery’s Amazing Statistics Program (JASP). -

04 – Everything You Want to Know About Correlation but Were
EVERYTHING YOU WANT TO KNOW ABOUT CORRELATION BUT WERE AFRAID TO ASK F R E D K U O 1 MOTIVATION • Correlation as a source of confusion • Some of the confusion may arise from the literary use of the word to convey dependence as most people use “correlation” and “dependence” interchangeably • The word “correlation” is ubiquitous in cost/schedule risk analysis and yet there are a lot of misconception about it. • A better understanding of the meaning and derivation of correlation coefficient, and what it truly measures is beneficial for cost/schedule analysts. • Many times “true” correlation is not obtainable, as will be demonstrated in this presentation, what should the risk analyst do? • Is there any other measures of dependence other than correlation? • Concordance and Discordance • Co-monotonicity and Counter-monotonicity • Conditional Correlation etc. 2 CONTENTS • What is Correlation? • Correlation and dependence • Some examples • Defining and Estimating Correlation • How many data points for an accurate calculation? • The use and misuse of correlation • Some example • Correlation and Cost Estimate • How does correlation affect cost estimates? • Portfolio effect? • Correlation and Schedule Risk • How correlation affect schedule risks? • How Shall We Go From Here? • Some ideas for risk analysis 3 POPULARITY AND SHORTCOMINGS OF CORRELATION • Why Correlation Is Popular? • Correlation is a natural measure of dependence for a Multivariate Normal Distribution (MVN) and the so-called elliptical family of distributions • It is easy to calculate analytically; we only need to calculate covariance and variance to get correlation • Correlation and covariance are easy to manipulate under linear operations • Correlation Shortcomings • Variances of R.V. -

Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10
International Journal of Environmental Research and Public Health Article Construct Validity and Reliability of the Work Environment Assessment Instrument WE-10 Rudy de Barros Ahrens 1,*, Luciana da Silva Lirani 2 and Antonio Carlos de Francisco 3 1 Department of Business, Faculty Sagrada Família (FASF), Ponta Grossa, PR 84010-760, Brazil 2 Department of Health Sciences Center, State University Northern of Paraná (UENP), Jacarezinho, PR 86400-000, Brazil; [email protected] 3 Department of Industrial Engineering and Post-Graduation in Production Engineering, Federal University of Technology—Paraná (UTFPR), Ponta Grossa, PR 84017-220, Brazil; [email protected] * Correspondence: [email protected] Received: 1 September 2020; Accepted: 29 September 2020; Published: 9 October 2020 Abstract: The purpose of this study was to validate the construct and reliability of an instrument to assess the work environment as a single tool based on quality of life (QL), quality of work life (QWL), and organizational climate (OC). The methodology tested the construct validity through Exploratory Factor Analysis (EFA) and reliability through Cronbach’s alpha. The EFA returned a Kaiser–Meyer–Olkin (KMO) value of 0.917; which demonstrated that the data were adequate for the factor analysis; and a significant Bartlett’s test of sphericity (χ2 = 7465.349; Df = 1225; p 0.000). ≤ After the EFA; the varimax rotation method was employed for a factor through commonality analysis; reducing the 14 initial factors to 10. Only question 30 presented commonality lower than 0.5; and the other questions returned values higher than 0.5 in the commonality analysis. Regarding the reliability of the instrument; all of the questions presented reliability as the values varied between 0.953 and 0.956. -
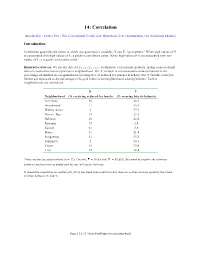
14: Correlation
14: Correlation Introduction | Scatter Plot | The Correlational Coefficient | Hypothesis Test | Assumptions | An Additional Example Introduction Correlation quantifies the extent to which two quantitative variables, X and Y, “go together.” When high values of X are associated with high values of Y, a positive correlation exists. When high values of X are associated with low values of Y, a negative correlation exists. Illustrative data set. We use the data set bicycle.sav to illustrate correlational methods. In this cross-sectional data set, each observation represents a neighborhood. The X variable is socioeconomic status measured as the percentage of children in a neighborhood receiving free or reduced-fee lunches at school. The Y variable is bicycle helmet use measured as the percentage of bicycle riders in the neighborhood wearing helmets. Twelve neighborhoods are considered: X Y Neighborhood (% receiving reduced-fee lunch) (% wearing bicycle helmets) Fair Oaks 50 22.1 Strandwood 11 35.9 Walnut Acres 2 57.9 Discov. Bay 19 22.2 Belshaw 26 42.4 Kennedy 73 5.8 Cassell 81 3.6 Miner 51 21.4 Sedgewick 11 55.2 Sakamoto 2 33.3 Toyon 19 32.4 Lietz 25 38.4 Three are twelve observations (n = 12). Overall, = 30.83 and = 30.883. We want to explore the relation between socioeconomic status and the use of bicycle helmets. It should be noted that an outlier (84, 46.6) has been removed from this data set so that we may quantify the linear relation between X and Y. Page 14.1 (C:\data\StatPrimer\correlation.wpd) Scatter Plot The first step is create a scatter plot of the data. -

CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (Moderately Hard)Or
5 COMPUTING CORRELATION COEFFICIENTS Ice Cream and Crimedistribute Difficulty Scale ☺ ☺ (moderately hard)or WHAT YOU WILLpost, LEARN IN THIS CHAPTER • Understanding what correlations are and how they work • Computing a simple correlation coefficient • Interpretingcopy, the value of the correlation coefficient • Understanding what other types of correlations exist and when they notshould be used Do WHAT ARE CORRELATIONS ALL ABOUT? Measures of central tendency and measures of variability are not the only descrip- tive statistics that we are interested in using to get a picture of what a set of scores 76 Copyright ©2020 by SAGE Publications, Inc. This work may not be reproduced or distributed in any form or by any means without express written permission of the publisher. Chapter 5 ■ Computing Correlation Coefficients 77 looks like. You have already learned that knowing the values of the one most repre- sentative score (central tendency) and a measure of spread or dispersion (variability) is critical for describing the characteristics of a distribution. However, sometimes we are as interested in the relationship between variables—or, to be more precise, how the value of one variable changes when the value of another variable changes. The way we express this interest is through the computation of a simple correlation coefficient. For example, what’s the relationship between age and strength? Income and years of education? Memory skills and amount of drug use? Your political attitudes and the attitudes of your parents? A correlation coefficient is a numerical index that reflects the relationship or asso- ciation between two variables. The value of this descriptive statistic ranges between −1.00 and +1.00. -

Statistical Analysis in JASP
Copyright © 2018 by Mark A Goss-Sampson. All rights reserved. This book or any portion thereof may not be reproduced or used in any manner whatsoever without the express written permission of the author except for the purposes of research, education or private study. CONTENTS PREFACE .................................................................................................................................................. 1 USING THE JASP INTERFACE .................................................................................................................... 2 DESCRIPTIVE STATISTICS ......................................................................................................................... 8 EXPLORING DATA INTEGRITY ................................................................................................................ 15 ONE SAMPLE T-TEST ............................................................................................................................. 22 BINOMIAL TEST ..................................................................................................................................... 25 MULTINOMIAL TEST .............................................................................................................................. 28 CHI-SQUARE ‘GOODNESS-OF-FIT’ TEST............................................................................................. 30 MULTINOMIAL AND Χ2 ‘GOODNESS-OF-FIT’ TEST. .......................................................................... -

Resources for Mini Meta-Analysis and Related Things Updated on June 25, 2018 Here Are Some Resources That I and Others Find
Resources for Mini Meta-Analysis and Related Things Updated on June 25, 2018 Here are some resources that I and others find useful. I know my mini meta SPPC article and Excel were not exhaustive and I didn’t cover many things, so I hope this resource page will give you some answers. I’ll update this page whenever I find something new or receive suggestions. Meta-Analysis Guides & Workshops • David Wilson, who wrote Practical Meta-Analysis, has a website containing PowerPoints and macros (for SPSS, Stata, and SAS) as well as some useful links on meta-analysis o I created an Excel template based on his slides (read the Excel page to see how this template differs from my previous SPPC template) • McShane and Böckenholt (2017) wrote an article in the Journal of Consumer Research similar to my mini meta paper. It comes with a very cool website that calculates meta- analysis for you: https://blakemcshane.shinyapps.io/spmetacase1/ • Courtney Soderberg from the Center for Open Science gave a mini meta-analysis workshop at SIPS 2017. All materials are publicly available: https://osf.io/nmdtq/ • Adam Pegler wrote a tutorial blog on using R to calculate mini meta based on my article • The founders of MetaLab at Stanford made video tutorials on meta-analysis in general • Geoff Cumming has a video tutorial on meta-analysis and other “new statistics” or read his Psychological Science article on the “new statistics” • Patrick Forscher’s meta-analysis syllabus and class materials are available online • A blog post containing 5 tips to understand and carefully -

Eight Things You Need to Know About Interpreting Correlations
Research Skills One, Correlation interpretation, Graham Hole v.1.0. Page 1 Eight things you need to know about interpreting correlations: A correlation coefficient is a single number that represents the degree of association between two sets of measurements. It ranges from +1 (perfect positive correlation) through 0 (no correlation at all) to -1 (perfect negative correlation). Correlations are easy to calculate, but their interpretation is fraught with difficulties because the apparent size of the correlation can be affected by so many different things. The following are some of the issues that you need to take into account when interpreting the results of a correlation test. 1. Correlation does not imply causality: This is the single most important thing to remember about correlations. If there is a strong correlation between two variables, it's easy to jump to the conclusion that one of the variables causes the change in the other. However this is not a valid conclusion. If you have two variables, X and Y, it might be that X causes Y; that Y causes X; or that a third factor, Z (or even a whole set of other factors) gives rise to the changes in both X and Y. For example, suppose there is a correlation between how many slices of pizza I eat (variable X), and how happy I am (variable Y). It might be that X causes Y - so that the more pizza slices I eat, the happier I become. But it might equally well be that Y causes X - the happier I am, the more pizza I eat. -

Chapter 11 -- Correlation
Contents 11 Association Between Variables 795 11.4 Correlation . 795 11.4.1 Introduction . 795 11.4.2 Correlation Coe±cient . 796 11.4.3 Pearson's r . 800 11.4.4 Test of Signi¯cance for r . 810 11.4.5 Correlation and Causation . 813 11.4.6 Spearman's rho . 819 11.4.7 Size of r for Various Types of Data . 828 794 Chapter 11 Association Between Variables 11.4 Correlation 11.4.1 Introduction The measures of association examined so far in this chapter are useful for describing the nature of association between two variables which are mea- sured at no more than the nominal scale of measurement. All of these measures, Á, C, Cramer's xV and ¸, can also be used to describe association between variables that are measured at the ordinal, interval or ratio level of measurement. But where variables are measured at these higher levels, it is preferable to employ measures of association which use the information contained in these higher levels of measurement. These higher level scales either rank values of the variable, or permit the researcher to measure the distance between values of the variable. The association between rankings of two variables, or the association of distances between values of the variable provides a more detailed idea of the nature of association between variables than do the measures examined so far in this chapter. While there are many measures of association for variables which are measured at the ordinal or higher level of measurement, correlation is the most commonly used approach. -

Sequence Ambiguity Determined from Routine Pol Sequencing Is a Reliable Tool for Real-Time Surveillance of HIV Incidence Trends
Infection, Genetics and Evolution 69 (2019) 146–152 Contents lists available at ScienceDirect Infection, Genetics and Evolution journal homepage: www.elsevier.com/locate/meegid Research paper Sequence ambiguity determined from routine pol sequencing is a reliable T tool for real-time surveillance of HIV incidence trends ⁎ Maja M. Lunara, Snježana Židovec Lepejb, Mario Poljaka, a Institute of Microbiology and Immunology, Faculty of Medicine, University of Ljubljana, Zaloška 4, Ljubljana 1105, Slovenia b Dr. Fran Mihaljevič University Hospital for Infectious Diseases, Mirogojska 8, Zagreb 10000, Croatia ARTICLE INFO ABSTRACT Keywords: Identifying individuals recently infected with HIV has been of great significance for close monitoring of HIV HIV-1 epidemic dynamics. Low HIV sequence ambiguity (SA) has been described as a promising marker of recent Incidence infection in previous studies. This study explores the utility of SA defined as a proportion of ambiguous nu- Sequence ambiguity cleotides detected in baseline pol sequences as a tool for routine real-time surveillance of HIV incidence trends at Mixed base calls a national level. Surveillance A total of 353 partial HIV-1 pol sequences obtained from persons diagnosed with HIV infection in Slovenia from 2000 to 2012 were studied, and SA was reported as a percentage of ambiguous base calls. Patients were characterized as recently infected by examining anti-HIV serological patterns and/or using commercial HIV-1 incidence assays (BED and/or LAg-Avidity assay). A mean SA of 0.29%, 0.14%, and 0.19% was observed for infections classified as recent by BED, LAg, or anti-HIV serological results, respectively. Welch's t-test showed a significant difference in the SA of recent versus long-standing infections (p < 0.001). -

9. Categorical Data Analysis
9. Categorical data analysis Now that we’ve covered the basic theory behind hypothesis testing it’s time to start looking at specific tests that are commonly used in psychology. So where should we start? Not every textbook agrees on where to start, but I’m going to start with “χ2 tests” (this chapter, pronounced “chi-square”1)and “t-tests” (Chapter 10). Both of these tools are very frequently used in scientific practice, and whilst they’re not as powerful as “regression” (Chapter 11) and “analysis of variance” (Chapter 12)they’re much easier to understand. The term “categorical data” is just another name for “nominal scale data”. It’s nothing that we haven’t already discussed, it’s just that in the context of data analysis people tend to use the term “categorical data” rather than “nominal scale data”. I don’t know why. In any case, categorical data analysis refers to a collection of tools that you can use when your data are nominal scale. However, there are a lot of different tools that can be used for categorical data analysis, and this chapter covers only a few of the more common ones. 9.1 The χ2 (chi-square) goodness-of-fit test The χ2 goodness-of-fit test is one of the oldest hypothesis tests around. It was invented by Karl Pearson around the turn of the century (Pearson 1900), with some corrections made later by Sir Ronald Fisher (Fisher 1922a). It tests whether an observed frequency distribution of a nominal variable matches an expected frequency distribution.