DOCSLIB.ORG

Modified Newtonian Dynamics an Introductory Review

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

MMOOddiififieedd NNeewwtotonniiaann DDyynnaammiicscs aann iinntrotrodduuctoctoryry rerevviieeww By RRicicccaarrddoo SSccaarrppaa EEuurrooppeeaann SSoouutthheerrnn OObbsseerrvvaattoorryy Everything started in 1933 with the work by Zwicky on the Coma cluster of galaxies, but were galaxy rotation curves to convince everybody there was dark matter in the universe Rotational velocity sensibly constant at large radii Implies an halo of non-luminous matter surrounds galaxies Halo density ∝ 1/r, mass diverges NGC 3198 (Begeman 1987) JuJussttifificicaattioionn ffoorr MMooddififyyiningg NNeewwttoonniaiann DDyynnaammicicss It is increasingly difficult to explain observations with non- baryonic dark matter. Effects of non-baryonic dark matter appears when and only when the acceleration of gravity (computed including only baryons) falls below a certain value, baptized a0. a0 is smaller than the smallest acceleration probed in the solar system, e.g., the acceleration of Mercury on Pluto is > a0 Thus the idea is simple: Newtonian dynamics breaks down below a0 PPrrooppoosseedd bbyy MM.. MMiillggrroomm iinn 11998833,, MONDMOND introducesintroduces aa newnew constantconstant ofof physics:physics: aa0 DDiisstatanncece ddooeessnn’’tt mmaattetter!r! What matters is the strength of the acceleration, not distance/size of objects (though for any given object low accelerations are reached at correspondingly large distances). MOND basic definition GM a Functional form derived from # a >> a0 " N = 2 rotation curves, where we know % r v = constant ⇒ a ∝1/r at large radii. $ Square root of Newtonian GMa acceleration ∝ 1/r. % 0 Multiplied by an acceleration we get & a << a0 " a = r right dimensions. ! An interpolation function derived empirically joins the two regimes ! ! (1/ 2 " a % " a2 % " a % µ$ ' = (a/a0)$1 + ' a = aµ a a 2 N $ ' # 0 & # 0 & ⇒ # a0 & ! ! Comparing MOND to real data DARK MATTER MOND GGaalalaxxieiess RRoottaattioionn CCuurrvveess wwitithh MMOONNDD Sanders & Verheijen 1998. Rotation curves derived from stellar light and 21cm hydrogen line GMa a = 0 r Velocity in km/s ! Distance in kpc FFitsits toto vv((rr)) ffoorr LLSSBB && HHSSBB GGaalalaxxieiess Sanders & McGaugh 02 -8 -2 a0=1.2 x10 cm s Does MOND fit any rotation curve? MOND fails to fit this one. MOND DARK MATTER This is a fake galaxy! Photometry from one object and velocity from another! In this case, a failure is a good thing! CCoouunntteerreexxaammppleless?!?! Romanowsky et al 2003 Claimed the discovery of 3 elliptical galaxies without dark matter halo. Dashed line: isothermal dark-matter halo Dotted line: constant mass-to-light ratio and NO dark matter. NNoo!! ThTheseese ggaallaaxxiieses aarere iinn NewNewtotonniiaann regregiimmee a>a0 Milgrom & Sanders 03 Dotted line: Newtonian prediction for constant M/L. Solid line: MOND prediction for the same M/L. TThhee TTuullylly--FFisishheerr v ⇐ RReelalatiotionn A relation between asymptotic velocity and luminosity of galaxies v 4 " L ! GGaallaaxxiieess’’ mmeeaann ssuurrfafaccee bbrriigghhtntneessss Σ High surface Brightness Low surface brightness Galaxy luminosity L = πr2Σ NNeewwtotonniiaann ddyynnaammiiccss aanndd TT--FF 2 2 (GM) v GM 4 v = 2 2 = 2 r M # r r 4 2 " v " 2 L = $ #L 2 L L {L = "r2# { r = "# T-F requires τ2Σ = const. ! ! But M/L= depends on stellar population, basically the same τ ! in all galaxies ! ! ! Surface brightness Σ varies significantly going from HSB to LSB galaxies and has nothing to do with M/L. Therefore Newton implies a link of two very unrelated quantities and predicts LSB and HSB galaxies to follow ! ! different T-F relations. TTuullllyy--FFiisshheerr rreellaatitioonn aanndd MMOONNDD 2 v GMa 4 L # M & = 0 ⇒ v " M = % ( L r r L $ L ' MOND requires M/L= constant ! ! AND The T-F is universal TThhee TTuullllyy--FFiisshheerr iiss uunniivveerrssaall aass MMOONNDD pprreeddiicctetedd Sanders & Verheijen Note that data for low surface brightness galaxies became available some 10 years later LSB Milgrom made its prediction. HSB McGaugh et al. 2000 Baryonic Tully-Fisher ApJL, 533, 99 Left: “Luminous mass” vs. rotational Velocity. Galaxies with v<90 km/s fall below the relation. Right: Including gas the relation is restored. The solid line has slope 4 The T-F is a relation between MASS and Velocity, as indeed predicted by MOND FFuunnddaammeennttaall pplalannee ooff eelliplliptticicaalsls LSB HSB Edge on view of the fundamental plane HSB define a a relation M/L ∝ L 0.25 LSB define an opposite trend M/L ∝ L -0.40 MMOONNDD eexxpplalannaattioionn ooff tthhee ttiltilt Tilt due to the different trend in gravitational filed strength In HSB the acceleration decreases with size In LSB the acceleration increases with size This is demonstrated by their average surface brightness MMOONNDD ddeeffinineess ssppeeccifificic ttrreennddss Log L/Lsun AccelerationAcceleration fromfrom velocityvelocity andand luminosityluminosity MOND agrees with real data over 7 orders of magnitudes UUltltrraa CCoommppaacctt DDwwaarrff GGaalalaxxieiess Drinkwater et al. 2003 DARK MATTER vs. MOND Dwarf galaxies are usually FULL UCD luminosity and size imply of dark matter with M/L~100, thus internal acceleration > a0 plenty of dark matter expected. everywhere, hence no dark matter should be found. NNoo DDaarrkk MMaatttteerr FFoouunndd inin UUCCDDss Accepted explanation: The dark matter was there but was lost together with the halo. Possible but NOT predicted and ad hoc MOND explanation: simple, elegant, fully logic and exactly as predicted! CClulusstteerrss ooff GGaalalaxxieiess (Sanders 1998) This may be the only place where MOND fails (by a factor 2. MOND predicts some baryonic matter still to be discovered GGrraavvititaattioionnaall lleennssiningg Difficult to address because MOND lack a relativistic Extension The Usual assumption is that light is bent twice has much as predicted by Newton’s law. That is: Compute field with MOND ⇒ Double the effect Warning: Gravitational lensing NEVER occur in MOND regime. SSttrroonngg LLeennssiningg The critical surface density required for strong lensing is 1 cH " = 0 F c 4# G [35] where F~10 is a dimensionless function of the lens and source redshifts , MOND applies at surface densities below ~ a /G ~ /5 ! Σ 0 Σc Strong lensing NEVER occurs in MOND regime WWee aarree lelefftt wwitithh wweeaakk lleennssiningg For a point source Mortlock & Turner 2001 we get an asymptotic deviation: 2" A = GMa M c 2 0 12 AM= 2” for M=10 Msun ! The deflection is independent from the impact parameter as much as rotation velocity is independent from r. RReeaall ddaattaa aaggrreeee wwitithh MMOONNDD BBuulglgee vvss BBlalacckk HHoolele mmaasssseess 4 MBH∝σ In presence of dark matter these two AND relations are difficult to M ∝L explain because from BH the tilt of the fundamental plane we get M/L∝L0.25. Piece of cake for MOND Ferrarese & Merritt because Astro-ph 0206222 M∝L∝σ4 MMOONNDD aanndd WWMMAAPP Power spectrum of temperature fluctuations in CMB McGaugh 2004 ApJ 611, 26 The ratio of the second to first peak depends on the baryon density BBaarryyoonn ddeennssitityy ffrroomm PPrrimimoorrddiaiall NNuuccleleoossyynntthheessisis McGaugh 2004 ApJ 611, 26 ΛCDM fit to WMAP data (Spergel et al. 2003) implies ωb=0.024 ± 0.001 MMooddeerrnn CCoossmmoolologgyy isis bbaasseedd oonn:: Cosmological principle FRW equations based on extrapolating General relativity to low accelerations (Newtonian limit). Thus: If any of these two hypothesis is wrong - MOND suggests the second - FRW equations are inappropriate to describe the universe. Progress in cosmology seems not to depend on one’s ability to describe observations within one particular FRW based model, rather on re-writing these equations within the contest of a new theory of gravity. PPrroobbiningg GGrraavvityity inin ththee LLooww AAcccceelelerraatiotionn RReeggimimee wwithith GGlolobbuulalarr CClulussteterrss By Riccardo Scarpa, Gianni Marconi & Roberto Gilmozzi European Southern Observatory MMeemmbbeerrsshhipip ddeeteterrmmininaatiotionn ddififfificcuultlt Target selection based on: HR diagram Proper motion (when possible) Radial velocity 35'x35' ωω CCeenntatauurri:i: vveeloloccityity ddisisppeerrssioionn ccoonnsstatanntt aatt lalarrggee rraaddii.ii. 2.1×10-8 cm s-2 MM 1155 ccoonnffirirmmss wwhhaatt ffoouunndd ffoorr ωω CCeenn 1.7×10-8 cm s-2 AlsoAlso inin NGCNGC 61716171 thethe velocityvelocity dispersiondispersion profileprofile flattensflattens outout atat largelarge radiiradii All data together 206 stars 1.4×10-8 cm s-2 CCoonncclulussioionnss ffoorr MMOONNDD Amazing ability to describe many properties of astronomical objects. Explains many data taken after it was proposed. Keep focus on demonstrating whether Newtonian dynamics fails at low accelerations. At present, I would compare MOND to Borh’s atom, which was based on un-justified assumptions and worked only for Hydrogen. This model eventually became the basis for quantum mechanics. Similarly, MOND might be the way to the next great step in physics..
Recommended publications
  • Dark Energy and Dark Matter As Inertial Effects Introduction

    Dark Energy and Dark Matter As Inertial Effects Introduction

    Dark Energy and Dark Matter as Inertial Effects Serkan Zorba Department of Physics and Astronomy, Whittier College 13406 Philadelphia Street, Whittier, CA 90608 [email protected] ABSTRACT A disk-shaped universe (encompassing the observable universe) rotating globally with an angular speed equal to the Hubble constant is postulated. It is shown that dark energy and dark matter are cosmic inertial effects resulting from such a cosmic rotation, corresponding to centrifugal (dark energy), and a combination of centrifugal and the Coriolis forces (dark matter), respectively. The physics and the cosmological and galactic parameters obtained from the model closely match those attributed to dark energy and dark matter in the standard Λ-CDM model. 20 Oct 2012 Oct 20 ph] - PACS: 95.36.+x, 95.35.+d, 98.80.-k, 04.20.Cv [physics.gen Introduction The two most outstanding unsolved problems of modern cosmology today are the problems of dark energy and dark matter. Together these two problems imply that about a whopping 96% of the energy content of the universe is simply unaccounted for within the reigning paradigm of modern cosmology. arXiv:1210.3021 The dark energy problem has been around only for about two decades, while the dark matter problem has gone unsolved for about 90 years. Various ideas have been put forward, including some fantastic ones such as the presence of ghostly fields and particles. Some ideas even suggest the breakdown of the standard Newton-Einstein gravity for the relevant scales. Although some progress has been made, particularly in the area of dark matter with the nonstandard gravity theories, the problems still stand unresolved.
  • Dark Matter and the Early Universe: a Review Arxiv:2104.11488V1 [Hep-Ph

    Dark Matter and the Early Universe: a Review Arxiv:2104.11488V1 [Hep-Ph

    Dark matter and the early Universe: a review A. Arbey and F. Mahmoudi Univ Lyon, Univ Claude Bernard Lyon 1, CNRS/IN2P3, Institut de Physique des 2 Infinis de Lyon, UMR 5822, 69622 Villeurbanne, France Theoretical Physics Department, CERN, CH-1211 Geneva 23, Switzerland Institut Universitaire de France, 103 boulevard Saint-Michel, 75005 Paris, France Abstract Dark matter represents currently an outstanding problem in both cosmology and particle physics. In this review we discuss the possible explanations for dark matter and the experimental observables which can eventually lead to the discovery of dark matter and its nature, and demonstrate the close interplay between the cosmological properties of the early Universe and the observables used to constrain dark matter models in the context of new physics beyond the Standard Model. arXiv:2104.11488v1 [hep-ph] 23 Apr 2021 1 Contents 1 Introduction 3 2 Standard Cosmological Model 3 2.1 Friedmann-Lema^ıtre-Robertson-Walker model . 4 2.2 A quick story of the Universe . 5 2.3 Big-Bang nucleosynthesis . 8 3 Dark matter(s) 9 3.1 Observational evidences . 9 3.1.1 Galaxies . 9 3.1.2 Galaxy clusters . 10 3.1.3 Large and cosmological scales . 12 3.2 Generic types of dark matter . 14 4 Beyond the standard cosmological model 16 4.1 Dark energy . 17 4.2 Inflation and reheating . 19 4.3 Other models . 20 4.4 Phase transitions . 21 5 Dark matter in particle physics 21 5.1 Dark matter and new physics . 22 5.1.1 Thermal relics . 22 5.1.2 Non-thermal relics .
  • Adrien Christian René THOB

    Adrien Christian René THOB

    THE RELATIONSHIP BETWEEN THE MORPHOLOGY AND KINEMATICS OF GALAXIES AND ITS DEPENDENCE ON DARK MATTER HALO STRUCTURE IN SIMULATED GALAXIES Adrien Christian René THOB A thesis submitted in partial fulfilment of the requirements of Liverpool John Moores University for the degree of Doctor of Philosophy. 26 April 2019 To my grand-parents, René Roumeaux, Christian Thob, Yvette Roumeaux (née Bajaud) and Anne-Marie Thob (née Léglise). ii Abstract Galaxies are among nature’s most majestic and diverse structures. They can play host to as few as several thousands of stars, or as many as hundreds of billions. They exhibit a broad range of shapes, sizes, colours, and they can inhabit vastly differing cosmic environments. The physics of galaxy formation is highly non-linear and in- volves a variety of physical mechanisms, precluding the development of entirely an- alytic descriptions, thus requiring that theoretical ideas concerning the origin of this diversity are tested via the confrontation of numerical models (or “simulations”) with observational measurements. The EAGLE project (which stands for Evolution and Assembly of GaLaxies and their Environments) is a state-of-the-art suite of such cos- mological hydrodynamical simulations of the Universe. EAGLE is unique in that the ill-understood efficiencies of feedback mechanisms implemented in the model were calibrated to ensure that the observed stellar masses and sizes of present-day galaxies were reproduced. We investigate the connection between the morphology and internal 9:5 kinematics of the stellar component of central galaxies with mass M? > 10 M in the EAGLE simulations. We compare several kinematic diagnostics commonly used to describe simulated galaxies, and find good consistency between them.
  • Chapter 3 the Mechanisms of Electromagnetic Emissions

    Chapter 3 the Mechanisms of Electromagnetic Emissions

    BASICS OF RADIO ASTRONOMY Chapter 3 The Mechanisms of Electromagnetic Emissions Objectives: Upon completion of this chapter, you will be able to describe the difference between thermal and non-thermal radiation and give some examples of each. You will be able to distinguish between thermal and non-thermal radiation curves. You will be able to describe the significance of the 21-cm hydrogen line in radio astronomy. If the material in this chapter is unfamiliar to you, do not be discouraged if you don’t understand everything the first time through. Some of these concepts are a little complicated and few non- scientists have much awareness of them. However, having some familiarity with them will make your radio astronomy activities much more interesting and meaningful. What causes electromagnetic radiation to be emitted at different frequencies? Fortunately for us, these frequency differences, along with a few other properties we can observe, give us a lot of information about the source of the radiation, as well as the media through which it has traveled. Electromagnetic radiation is produced by either thermal mechanisms or non-thermal mechanisms. Examples of thermal radiation include • Continuous spectrum emissions related to the temperature of the object or material. • Specific frequency emissions from neutral hydrogen and other atoms and mol- ecules. Examples of non-thermal mechanisms include • Emissions due to synchrotron radiation. • Amplified emissions due to astrophysical masers. Thermal Radiation Did you know that any object that contains any heat energy at all emits radiation? When you’re camping, if you put a large rock in your campfire for a while, then pull it out, the rock will emit the energy it has absorbed as radiation, which you can feel as heat if you hold your hand a few inches away.
  • The Protection of Frequencies for Radio Astronomy 1

    The Protection of Frequencies for Radio Astronomy 1

    JOURNAL OF RESEARCH of the National Bureau of Standards-D. Radio Propagation Vol. 67D, No. 2, March- April 1963 b The Protection of Frequencies for Radio Astronomy 1 R. 1. Smith-Rose President, International Scientific Radio Union (R eceived November 5, 1962) The International T elecommunications Union in its Geneva, 1959 R adio R egulations r recognises the Radio Astronomy Service in t he two following definitions: N o. 74 Radio A st1" onomy: Astronomy based on t he reception of waves of cos mi c origin. No. 75 R adio A st1"onomy Se1"vice: A service involving the use of radio astronomy. This service differs, however, from other r adio services in two important respects. 1. It does not itself originate any radio waves, and therefore causes no interference to any other service. L 2. A large proportion of its activity is conducted by the use of reception techniques which are several orders of magnit ude )]).ore sensitive than those used in other ra dio services. In order to pursue his scientific r esearch successfully, t he radio astronomer seeks pro­ tection from interference first, in a number of bands of frequencies distributed t hroughout I t he s p ~ct run:; and secondly:. 1~10r e complete and s p ec i~c prote.ction fOl: t he exact frequency bands III whIch natural radIatIOn from, or absorptIOn lD, cosmIc gases IS known or expected to occur. The International R egulations referred to above give an exclusive all ocation to one freq uency band only- the emission line of h ydrogen at 1400 to 1427 Mc/s.
  • Particle Dark Matter an Introduction Into Evidence, Models, and Direct Searches

    Particle Dark Matter an Introduction Into Evidence, Models, and Direct Searches

    Particle Dark Matter An Introduction into Evidence, Models, and Direct Searches Lecture for ESIPAP 2016 European School of Instrumentation in Particle & Astroparticle Physics Archamps Technopole XENON1T January 25th, 2016 Uwe Oberlack Institute of Physics & PRISMA Cluster of Excellence Johannes Gutenberg University Mainz http://xenon.physik.uni-mainz.de Outline ● Evidence for Dark Matter: ▸ The Problem of Missing Mass ▸ In galaxies ▸ In galaxy clusters ▸ In the universe as a whole ● DM Candidates: ▸ The DM particle zoo ▸ WIMPs ● DM Direct Searches: ▸ Detection principle, physics inputs ▸ Example experiments & results ▸ Outlook Uwe Oberlack ESIPAP 2016 2 Types of Evidences for Dark Matter ● Kinematic studies use luminous astrophysical objects to probe the gravitational potential of a massive environment, e.g.: ▸ Stars or gas clouds probing the gravitational potential of galaxies ▸ Galaxies or intergalactic gas probing the gravitational potential of galaxy clusters ● Gravitational lensing is an independent way to measure the total mass (profle) of a foreground object using the light of background sources (galaxies, active galactic nuclei). ● Comparison of mass profles with observed luminosity profles lead to a problem of missing mass, usually interpreted as evidence for Dark Matter. ● Measuring the geometry (curvature) of the universe, indicates a ”fat” universe with close to critical density. Comparison with luminous mass: → a major accounting problem! Including observations of the expansion history lead to the Standard Model of Cosmology: accounting defcit solved by ~68% Dark Energy, ~27% Dark Matter and <5% “regular” (baryonic) matter. ● Other lines of evidence probe properties of matter under the infuence of gravity: ▸ the equation of state of oscillating matter as observed through fuctuations of the Cosmic Microwave Background (acoustic peaks).
  • DARK MATTER and NEUTRINOS Arxiv:1711.10564V1 [Physics.Pop-Ph]

    DARK MATTER and NEUTRINOS Arxiv:1711.10564V1 [Physics.Pop-Ph]

    Physics Education 1 dateline DARK MATTER AND NEUTRINOS Gazal Sharma1, Anu2 and B. C. Chauhan3 Department of Physics & Astronomical Science School of Physical & Material Sciences Central University of Himachal Pradesh (CUHP) Dharamshala, Kangra (HP) INDIA-176215. [email protected] [email protected] [email protected] (Submitted 03-08-2015) Abstract The Keplerian distribution of velocities is not observed in the rotation of large scale structures, such as found in the rotation of spiral galaxies. The deviation from Keplerian distribution provides compelling evidence of the presence of non-luminous matter i.e. called dark matter. There are several astrophysical motivations for investigating the dark matter in and around the galaxy as halo. In this work we address various theoretical and experimental indications pointing towards the existence of this unknown form of matter. Amongst its constituents neutrino is one of the most prospective candidates. We know the neutrinos oscillate and have tiny masses, but there are also signatures for existence of heavy and light sterile neutrinos and possibility of their mixing. Altogether, the role of neutrinos is of great interests in cosmology and understanding dark matter. arXiv:1711.10564v1 [physics.pop-ph] 23 Nov 2017 1 Introduction revealed in 2013 that our Universe contains 68:3% of dark energy, 26:8% of dark matter, and only 4:9% of the Universe is known mat- As a human being the biggest surprise for us ter which includes all the stars, planetary sys- was, that the Universe in which we live in tems, galaxies, and interstellar gas etc.. This is mostly dark.
  • Effective Description of Dark Matter As a Viscous Fluid

    Effective Description of Dark Matter As a Viscous Fluid

    Motivation Framework Perturbation theory Effective viscosity Results FRG improvement Conclusions Effective Description of Dark Matter as a Viscous Fluid Nikolaos Tetradis University of Athens Work with: D. Blas, S. Floerchinger, M. Garny, U. Wiedemann . N. Tetradis University of Athens Effective Description of Dark Matter as a Viscous Fluid Motivation Framework Perturbation theory Effective viscosity Results FRG improvement Conclusions Distribution of dark and baryonic matter in the Universe Figure: 2MASS Galaxy Catalog (more than 1.5 million galaxies). N. Tetradis University of Athens Effective Description of Dark Matter as a Viscous Fluid Motivation Framework Perturbation theory Effective viscosity Results FRG improvement Conclusions Inhomogeneities Inhomogeneities are treated as perturbations on top of an expanding homogeneous background. Under gravitational attraction, the matter overdensities grow and produce the observed large-scale structure. The distribution of matter at various redshifts reflects the detailed structure of the cosmological model. Define the density field δ = δρ/ρ0 and its spectrum hδ(k)δ(q)i ≡ δD(k + q)P(k): . N. Tetradis University of Athens Effective Description of Dark Matter as a Viscous Fluid 31 timation method in its entirety, but it should be equally valid. 7.3. Comparison to other results Figure 35 compares our results from Table 3 (modeling approach) with other measurements from galaxy surveys, but must be interpreted with care. The UZC points may contain excess large-scale power due to selection function effects (Padmanabhan et al. 2000; THX02), and the an- gular SDSS points measured from the early data release sample are difficult to interpret because of their extremely broad window functions.
  • A Derivation of Modified Newtonian Dynamics

    A Derivation of Modified Newtonian Dynamics

    Journal of The Korean Astronomical Society http://dx.doi.org/10.5303/JKAS.2013.46.2.93 46: 93 ∼ 96, 2013 April ISSN:1225-4614 c 2013 The Korean Astronomical Society. All Rights Reserved. http://jkas.kas.org A DERIVATION OF MODIFIED NEWTONIAN DYNAMICS Sascha Trippe Department of Physics and Astronomy, Seoul National University, Seoul 151-742, Korea E-mail : [email protected] (Received February 14, 2013; Revised March 20, 2013; Accepted March 29, 2013) ABSTRACT Modified Newtonian Dynamics (MOND) is a possible solution for the missing mass problem in galac- tic dynamics; its predictions are in good agreement with observations in the limit of weak accelerations. However, MOND does not derive from a physical mechanism and does not make predictions on the transitional regime from Newtonian to modified dynamics; rather, empirical transition functions have to be constructed from the boundary conditions and comparisons with observations. I compare the formalism of classical MOND to the scaling law derived from a toy model of gravity based on virtual massive gravitons (the “graviton picture”) which I proposed recently. I conclude that MOND naturally derives from the “graviton picture” at least for the case of non-relativistic, highly symmetric dynamical systems. This suggests that – to first order – the “graviton picture” indeed provides a valid candidate for the physical mechanism behind MOND and gravity on galactic scales in general. Key words : Gravitation — Galaxies: kinematics and dynamics −10 −2 1. INTRODUCTION where x = ac/am, am ≈ 10 ms is Milgrom’s con- stant, and µ(x)isa transition function with the asymp- “ It is worth remembering that all of the discus- totic behavior µ(x) → 1 for x ≫ 1 and µ(x) → x for sion [on dark matter] so far has been based on x ≪ 1.
  • Modified Newtonian Dynamics

    Modified Newtonian Dynamics

    J. Astrophys. Astr. (December 2017) 38:59 © Indian Academy of Sciences https://doi.org/10.1007/s12036-017-9479-0 Modified Newtonian Dynamics (MOND) as a Modification of Newtonian Inertia MOHAMMED ALZAIN Department of Physics, Omdurman Islamic University, Omdurman, Sudan. E-mail: [email protected] MS received 2 February 2017; accepted 14 July 2017; published online 31 October 2017 Abstract. We present a modified inertia formulation of Modified Newtonian dynamics (MOND) without retaining Galilean invariance. Assuming that the existence of a universal upper bound, predicted by MOND, to the acceleration produced by a dark halo is equivalent to a violation of the hypothesis of locality (which states that an accelerated observer is pointwise inertial), we demonstrate that Milgrom’s law is invariant under a new space–time coordinate transformation. In light of the new coordinate symmetry, we address the deficiency of MOND in resolving the mass discrepancy problem in clusters of galaxies. Keywords. Dark matter—modified dynamics—Lorentz invariance 1. Introduction the upper bound is inferred by writing the excess (halo) acceleration as a function of the MOND acceleration, The modified Newtonian dynamics (MOND) paradigm g (g) = g − g = g − gμ(g/a ). (2) posits that the observations attributed to the presence D N 0 of dark matter can be explained and empirically uni- It seems from the behavior of the interpolating function fied as a modification of Newtonian dynamics when the as dictated by Milgrom’s formula (Brada & Milgrom gravitational acceleration falls below a constant value 1999) that the acceleration equation (2) is universally −10 −2 of a0 10 ms .
  • 1 Spectroscopic Study of Unique Line Broadening and Inversion in Low

    1 Spectroscopic Study of Unique Line Broadening and Inversion in Low

    Spectroscopic study of unique line broadening and inversion in low pressure microwave generated water plasmas R. L. Mills,a) P. C. Ray, R. M. Mayo, M. Nansteel, B. Dhandapani BlackLight Power, Inc., 493 Old Trenton Road, Cranbury, NJ 08512 Jonathan Phillips University of New Mexico, Dept. of Chemical and Nuclear Engineering, 203 Farris Engineering, Albuquerque, NM 87131 It was demonstrated that low pressure (~ 0.2 Torr) water vapor plasmas generated in a 10 mm inner diameter quartz tube with an Evenson microwave cavity show at least two features which are not explained by conventional plasma models. First, significant (> 2.5 Å) hydrogen Balmer α line broadening, of constant width, up to 5 cm from the microwave coupler was recorded. Only hydrogen, and not oxygen, showed significant line broadening. This feature, observed previously in hydrogen-containing mixed gas plasmas generated with high voltage dc and rf discharges was explained by some researchers to result from acceleration of hydrogen ions near the cathode. This explanation cannot apply to the line broadening observed in the (electrodeless) microwave plasmas generated in this work, particularly at distances as great as 5 cm from the microwave coupler. Second, inversion of the line intensities of both the Lyman and Balmer series, again, at distances up to 5 cm from the coupler, were observed. The line inversion suggests the existence of a hitherto unknown source of pumping of the 1 optical power in plasmas. Finally, it is notable that other aspects of the plasma including the OH* rotational temperature and low electron concentrations are quite typical of plasmas of this type.
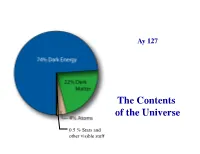
  • The Contents of the Universe

    The Contents of the Universe

    Ay 127! The Contents of the Universe 0.5 % Stars and other visible stuff Supernovae alone ⇒ Accelerating expansion ⇒ Λ > 0 CMB alone ⇒ Flat universe ⇒ Λ > 0 Any two of SN, CMB, LSS ⇒ Dark energy ~70% Also in agreement with the age estimates (globular clusters, nucleocosmochronology, white dwarfs) Today’s Best Guess Universe Age: Best fit CMB model - consistent with ages of oldest stars t0 =13.82 ± 0.05 Gyr Hubble constant: CMB + HST Key Project to -1 -1 measure Cepheid distances H0 = 69 km s Mpc € Density of ordinary matter: CMB + comparison of nucleosynthesis with Lyman-a Ωbaryon = 0.04 € forest deuterium measurement Density of all forms of matter: Cluster dark matter estimate CMB power spectrum 0.31 € Ωmatter = Cosmological constant: Supernova data, CMB evidence Ω = 0.69 for a flat universe plus a low € Λ matter density € The Component Densities at z ~ 0, in critical density units, assuming h ≈ 0.7 Total matter/energy density: Ω0,tot ≈ 1.00 From CMB, and consistent with SNe, LSS From local dynamics and LSS, and Matter density: Ω0,m ≈ 0.31 consistent with SNe, CMB From cosmic nucleosynthesis, Baryon density: Ω0,b ≈ 0.045 and independently from CMB Luminous baryon density: Ω0,lum ≈ 0.005 From the census of luminous matter (stars, gas) Since: Ω0,tot > Ω0,m > Ω0,b > Ω0,lum There is baryonic dark matter There is non-baryonic dark matter There is dark energy The Luminosity Density Integrate galaxy luminosity function (obtained from large redshift surveys) to obtain the mean luminosity density at z ~ 0 8 3 SDSS, r band: ρL = (1.8 ± 0.2) 10 h70 L/Mpc 8 3 2dFGRS, b band: ρL = (1.4 ± 0.2) 10 h70 L/Mpc Luminosity To Mass Typical (M/L) ratios in the B band along the Hubble sequence, within the luminous portions of galaxies, are ~ 4 - 5 M/L This includes some dark matter - for pure stellar populations, (M/L) ratios should be slightly lower.