DOCSLIB.ORG

Room Acoustics Special,Issue

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Room Acoustics Special,Issue ROOM ACOUSTICS SPECIAL,ISSUE • Computet Simulation • Neural ,Networks • Sabine Rooms • Office Acoustics Australian Acoustical Society Vol. 23 No.3 December 1995 Yoor PC Here's What it Does: AnyPC-desO.!OPOf pcrt.llIe-c.., be II'lnslllfftled llIlO. K_m ko aly ~ . D 'III'hy$l C SlW (....., ._ Iloo. ......... • TmnsientCaptureandFFT •n" NI'S'lIfI IKJ.". lhrs!:omiwQ 4!I6clllof lJE govftyOlll lo9"l. • Linear andPower Spectrum pOfUble jMt,~m.nt • Synchronous Average • RPM based Spectral Analysis • Runup and Coastdown Waterfalls • Order Tracking • Transfer Function andCoherence + • Realtime Zoom • Correlation Ant-", proteet!'ll • DemodulationandHilbert Transform II ilCAllCsand "",,," 'llM 'll DSP • Stepped SineTransfer Function prOClKloQI'SfofllllM 10000lr>on01 lIlIl • AcousticIntensity ...- ffT ....... • RealtimeV-i Octave Analysis • Shock Response Spectrum • DiskRecord andPlayback • Closed Loop Shaker Control • 1to 16ADCInput Channels One Dynamic Instrument • Multiple DACOutput Channels The DP410FFTAnalvzer ;sfast becomingthe instrument ofchoicefordrnamics solutions. ~lia~fitjj EDITORIALCOMM.,." Neville Fletcher Marion Burgess Vol 23 No3 CONTENTS December 1995 JosephLai ASSISTING EDITOR: ARTICLES LeighKenna BUSINESS MANAGER: Computer Simulation Techniques for Acoustical Design of Rooms MrsLeighWallbank JHRlndel 81 Predicting the Acoustics of Concert Halls Using an Artifical ForAll GeneralBusiness Neural Network (subscriptions, extracopies, back issues,advertising,etc.) F Fricke and C Hoon Haan 87 MrsLeighWallbank Some Notes on Sabine Rooms POBox579 CRONULLANSW2230' DABles 97 Tel (02)5284362 Fax(02)5239637 Notes on Office Acoustics BMurray 105 ForAll EditorialMatters (articles, reports, news, bookreviews, newproducls,etc) TheEditor,AcousticsAustralia Acoustics &Vibration Centre Australian Defence ForceAcademy CANBERRA ACT2600 Tel (06)2688241 Fax(06)2688276 email:[email protected] AcousticsAustraliaispublishedbylhe Diary .... AuslralianAcousticaiSociety (A.C.N.OOO712658) Acoustics Australia Informalion ..... Responsibility lorthecontents ofarticles AustralianAcousticaISocie1ylnformation ... rests upon the authors and not the Australian Acoustical Society. Articles arecopyright,butmaybereproducedin fullprovided adequate reference isquol­ ed.AcousticsAustraliaisabstracledand indexed in Engineering Index, Physics Abstracts, Acoustics Abstracts & Noise: Abstracts,Reviews. Printed by Cronulla Printing CoPtyLtd, 16CronullaPlaza, CRONULLA2230 Tel (02)5235954, COVER: Fax(02)5239637 Reflection of spherical waves from straight edge object- see article by Zhu and McKerrow. ISSN0814-6039 Vol. 23 (1995) No.3 - 77 AUSTRALIAN ACOUSTICAL SOCIETY SUSTAINING MEMBERS ASSDelAnoN Of AUSTRAUAN BRUEL&KJAfRAUSTRALlAPTY LTD NAPSlLEHTfLO AcousnCALCOHSULTANTS PO90Xm. seEllJCKl.At.OST, SCIENCE CENTRE FOUNDATION TfMEYHIUS :z0B,6 Q.AYTON3168 PRlVATEBAG1. CHAOWICKTECH NOlOGY P!A CEENGINEERI'«;P TYLTtI DAALlNGIiJRST2010 9COOK STAEET, 2I2O t.lARlGOlOST F~STVILLE2OEl 7 ASSOClAnOHOf AEVESBY2212 CSR QYPROCK & BRADFORDINSULATION NOISECOfmIOL ENGINEERING ADeLACOMPOSITEPRODUCTS LEVEL5,9 HELP STREET P,O,BOX484 ~NG CHATSWOOD 2067 73-105 FRANKS TOtHIANDE RD. MT.EUZA3930 DANDENONa3175 eMONA1NSTAUMENTS Pt\. BARClAYENGINEERlHG 86PARRAMATTAROAO SAFElYEOUPWENT AUSTRALlA.Pi\. 12·16 CATAlANORO. CAMPEROOWN 2050 35/1-3JUBll EEAVI:. CANNINilVAl..f61S5 ENVlROHMOOALNOISECONlROLP,l WARRIEWOOD 2102 BHPSTEEL, SOAJVERSDERQAO PVRonK PTYLTD SKEETaCOILPRODUCTS DIVISION O!IPPIHGtKlRTON2170 1.7 UAGOWAR 1'10, POBOXn, GP EMBELTOfol&COPTYLTD GIRRAWEEN214.5 t 41-1049BAKERS ROAO PORTKEI.lBLA25OIS WARBURTON FRANKl coeURC33058 BlLSO MAUSTlIAUAPTY lTD OMsion01een·IRH IM dustnes Pf)'Ud INC COAPORATlONPTYlTO 19TEPKO ROAD, 1<10 BUFl'NOODHIGHWAY 22Cl£ElANDROAO TEARYHIu.s2OEl4 BUAlflOOO31 25 OAKLEIGH SCUTH3167 BORALPLASTEABOARD JOYCEAUSTllAUA WOFlKCOVEFlACOUSTICS 616LOOIMERST. -, So9BRIDGERQAO, 132 LONDONDERRY1'1 0 PORTMELBOURNE3207 • MOOREB.l.NK211O LONOONDeARY2753 QuHMln PII10118011 455S r" 10118ol14600 ~fEE3 :9 .....olemAoot"' ... pt,[0315>S1271 ,­ ~ le ee1(r r.. «()3j!65 f956 .... jO.lIY.b1956 _s...... WaIOS /4Cl r.. Pll102I148050l4 Soolll _ . /ffl r.. /02114810 16 lOBI3651ooo r" (Il8j36!>lOOl 78 · Vol. 23 ( 1995) No _3 Acousuca Australla It is now j us t 100 years s ince the from each other and from extraneous did, however, leave also a memorable PrcsidentofHarvardUnivcr1ity dire<:led noises." These criteria cou ld hardly be collection of buildings for which he Wal1acc Clement Sabine, then a young expressed better today, a century later. contributed the acousli c design. The ASlIislanl Professor (i.e. Lect urer) in With only the simplest equipment ­ best known of these is Symphony Hall in physics 10 " propose changes for remember that microphones and valve Boslon,of'C nedin 1890 and still widely remed ying the acoustical difficulties in amplifien had nOIyet been invented- he regarded as one of the world's great the reerore-recm of the Fogg Art wenl on 10 eslablish his famous law for concert halls, &8 well as Ihe first 10 be Museum , I bui lding that had just been reverbera tion lime as a function of desi iJ:nedusingquanlir ative acou slic com pleted" How famil iar those words volume and surfaceab'lOrption, andlater princip les. He laler went on to design sound to the mod ern acous tical went on 10 measure Ihe absorpti on the acoustics of many well known consultan t! ln the course of remedy ing faetOl'1l for many materials and surfaces, buildings, ineluding the Caehedral of St u l lies~ , those " di ffi c Sabine establ ished u well as trans mission losses and many the modem scienc e of archi tectu ral otber properties of practical inte rest John the Divine in I\ ew York, wh ich is acoustics. It is pleas ing 10 record that His papers were published. for the most the largest Golhic cathe dral in the world Harvard recognise d his contribu tion s part , in architectural and tec hni cal The subjeCI has. of course, and later conferred on him an honorary jou rnals rather than in the scientif ic progressed I great deal since Sabin e's Doctcrate of Sclence c he had no PhD· luerarure, so Ihat they would bcavai lable time, but his fundam ental insights still and made him the first Dean of the new to membcn of the profess ion. sland. In this issue, our contrib utors Graduate Schoo l of Appl ied Science. Sab ine 's experimental work Will show how modern techn iques of In his first published paper in 1898, mcticulous, and it was said that he "was mathem atical analy sis and comp uter Sabine wrote: "In order tha t heari ng may reluctant to publish the results of an modelling can give us both an improved be geed in any auditorium, it is cxperiment until he was sure it had been understand ing of lheacouslieproperties necessary that the sound should be done 50 well that nobody would ever of halls and a set of tools not only for suffieiet1tly loud; that the simultan eous need to repeat il." Conseq uently the cs or e~ i s lin g improving the ac o u~ t i halls componern s of a compl ex sound shou ld volume of his publications is not very but , even mor e importantly, for maintain their proper relative intens ities; large. though it includes such innovative opt imizing in advance Ihe performanc e and that lhc success ive sounds in rapidl y lechn iques Ii the vis ualisation of of halls thai are'still in the design stage. moving articulation, either in speec h or aco uslic wavefro nts using spark music, should be clear and distinct, free pholography in small -scale models. He NevjlfeFll'lchl' r COUNCIL OF THE AUSTRALIAN ACOUSTICAL SOCIETY President NProf Charles Don Vice-President Dr Graema Yates Treasu rer Mr Peter Heinze Gene ral Secretary Mr David Watkins Federal Registrar Mr Ray Piesse Cha irman, Sianding Com millee on Membershi p Mr Ken Cook Arch ivist Mr David Watkins Councillors Ne w So uth Wi les Quee nsl l nd South Australia Victor ia We .temAUltral ia Dr Norman Carter Mr Russell Brown Mr Peter He inze A/Prof Charl e s Don MrNorbert Gabriels Dr Stephen Samuels Mr Ross Palmer Mr Byron Martin Mr Claudlo Senese Dr Graeme Yates scoosrcsAustralia Vol 23 (1995) No, 3-79 NO NONSENSE CONTROL OF ENTERTAINMENT NOISE IN FUNCTION & ENTERTAINME NT VENUES ~ ilONT!EC C"lC> Matrix Industries Ply . Ltd. patented wall ties provide structural support while reducing Programmable Noise Monitor transmission of structure borne vibrations (previoosly known as Gax om 2376) Resilient mounting systems are available for all masonry and plasterboard walls and lightweight Simply dial up the Tl;'l uired Sound Threshold f1oatingftoors. • Trigger Range 60 to 120DB Matrix Industries products are reduc ing noise in • Weighting: Linear, A or Low Pass Filter studios and theatres throughout Australia E nq \l ~ ;es and Sakol; Visual Display Unit indicates approaching Thre shold MATRIX INDUSTRIES PTY LTD • Controls ;n lockable Stee1 Cabinet 3 RICHAROSON STREET, TAREE NSW 2430 PH/f AX: (065 ) 522 206 AlsoDisj,jbuled by BRUNSWICK SALES PTY. LTD. 49 LEICESTER STREE T, FITZR OY VIC 306 5 Ph : (03) 9419 0099 Fax (03) 9419 2218 56AThomf"O'lS,_ ~."..,NSW 2047 ~ Dn.", T. ~G18 470 179 Tdif.. , (02) 819 6N8 A(U·Vl8 fledron'cs POIloxW16 A c o u ,I i c g n d V i b r o l i 0 n E I e c l r on i e , W......., h. , NSW 1046 I;or much less th.m anywhere else Calihralion AaJ-VlBEIectronics repa.lr]acillll&J can helpyou with calibration. repair or hire of instrumenls • Sound Level Meters & Filters supplie<l bydiflerent • Noise Dose M eters manufacturers. • Calibrators & Pistonphones \Ve also trade in new and used instruments • N o ise Loggers & Noise Analy ze rs an
Load more

Recommended publications
  • Industrial Noise Control and Acoustics
    Industrial Noise Control and Acoustics Randall F. Barron Louisiana Tech University Ruston, Louisiana, U.S.A. Marcel Dekker, Inc. New York • Basel Copyright © 2001 by Marcel Dekker, Inc. All Rights Reserved. Copyright © 2003 Marcel Dekker, Inc. LibraryofCongressCataloging-in-PublicationData AcatalogrecordforthisbookisavailablefromtheLibraryofCongress. ISBN:0-8247-0701-X Thisbookisprintedonacid-freepaper. Headquarters MarcelDekker,Inc. 270MadisonAvenue,NewYork,NY10016 tel:212-696-9000;fax:212-685-4540 EasternHemisphereDistribution MarcelDekkerAG Hutgasse4,Postfach812,CH-4001Basel,Switzerland tel:41-61-260-6300;fax:41-61-260-6333 WorldWideWeb http://www.dekker.com The publisher offers discounts on this book when ordered in bulk quantities, For more information, write to Special Sales/Professional Marketing at the headquarters address above. Copyright # 2003 by Marcel Dekker, Inc. All Rights Reserved. Neither this book nor any part may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, microfilming, and recording, or by any information storage retrieval system, without permission in writing from the publisher. Current printing (last digit): 10987654321 PRINTED IN THE UNITED STATES OF AMERICA Copyright © 2003 Marcel Dekker, Inc. Preface Since the Walsh-Healy Act of 1969 was amended to include restrictions on the noise exposure of workers, there has been much interest and motivation in industry to reduce noise emitted by machinery. In addition to concerns about air and water pollution by contaminants, efforts have also been direc- ted toward control of environmental noise pollution. In response to these stimuli, faculty at many engineering schools have developed and introduced courses in noise control, usually at the senior design level. It is generally much more effective to design ‘‘quietness’’ into a product than to try to ‘‘fix’’ the noise problem in the field after the product has been put on the market.
    [Show full text]
  • Definition and Measurement of Sound Energy Level of a Transient Sound Source
    J. Acoust. Soc. Jpn. (E) 8, 6 (1987) Definition and measurement of sound energy level of a transient sound source Hideki Tachibana,* Hiroo Yano,* and Koichi Yoshihisa** *Institute of Industrial Science , University of Tokyo, 7-22-1, Roppongi, Minato-ku, Tokyo, 106 Japan **Faculty of Science and Technology, Meijo University, 1-501, Shiogamaguti, Tenpaku-ku, Nagoya, 468 Japan (Received 1 May 1987) Concerning stationary sound sources, sound power level which describes the sound power radiated by a sound source is clearly defined. For its measuring methods, the sound pressure methods using free field, hemi-free field and diffuse field have been established, and they have been standardized in the international and national stan- dards. Further, the method of sound power measurement using the sound intensity technique has become popular. On the other hand, concerning transient sound sources such as impulsive and intermittent sound sources, the way of describing and measuring their acoustic outputs has not been established. In this paper, therefore, "sound energy level" which represents the total sound energy radiated by a single event of a transient sound source is first defined as contrasted with the sound power level. Subsequently, its measuring methods by two kinds of sound pressure method and sound intensity method are investigated theoretically and experimentally on referring to the methods of sound power level measurement. PACS number : 43. 50. Cb, 43. 50. Pn, 43. 50. Yw sources, the way of describing and measuring their 1. INTRODUCTION acoustic outputs has not been established. In noise control problems, it is essential to obtain In this paper, "sound energy level" which repre- the information regarding the noise sources.
    [Show full text]
  • Derivation of the Sabine Equation: Conservation of Energy
    UIUC Physics 406 Acoustical Physics of Music Derivation of the Sabine Equation: Conservation of Energy Consider a large room of volume V = HWL (m3) with perfectly reflecting walls, filled with a uniform, steady-state (i.e. equilibrium) acoustic energy density wrtfa ,, at given frequency f (Hz) within the volume V of the room. Uniform energy density means that a given time t: 3 waa r,, t f w t , f constant (SI units: Joules/m ). The large room also has a small opening of area A (m2) in it, as shown in the figure below: H V A I rt,, f ac nAˆˆ, An W L In the steady-state, the rate of acoustical energy Wa input e.g. by a point sound source within the large room equals the rate at which acoustical energy is “leaking” out of the room through the hole of area A, i.e. the acoustical power input by the sound source in the room into the room = the acoustical power leaving the room through the hole of area A. In this idealized model of a room with perfectly reflecting walls, the hole of area A thus represents absorption of sound in a real room with finite reflectivity walls, i.e. walls that have some absorption associated with them. Suppose at time t = 0 the sound source in the room {located far from the hole} is turned off. Since the sound energy density is uniform in the room, the sound energy contained in the room Wtf,,,, wrtfdrwtf 33 drwtfV , will thus decrease with time, since aaVV a a acoustical energy is (slowly) leaking out of the room through the opening of area A.
    [Show full text]
  • Measurement of Total Sound Energy Density in Enclosures at Low Frequencies Abstract of Paper
    View metadata,Downloaded citation and from similar orbit.dtu.dk papers on:at core.ac.uk Dec 17, 2017 brought to you by CORE provided by Online Research Database In Technology Measurement of total sound energy density in enclosures at low frequencies Abstract of paper Jacobsen, Finn Published in: Acoustical Society of America. Journal Link to article, DOI: 10.1121/1.2934233 Publication date: 2008 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Jacobsen, F. (2008). Measurement of total sound energy density in enclosures at low frequencies: Abstract of paper. Acoustical Society of America. Journal, 123(5), 3439. DOI: 10.1121/1.2934233 General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. WEDNESDAY MORNING, 2 JULY 2008 ROOM 242B, 8:00 A.M. TO 12:40 P.M. Session 3aAAa Architectural Acoustics: Case Studies and Design Approaches I Bryon Harrison, Cochair 124 South Boulevard, Oak Park, IL, 60302 Witew Jugo, Cochair Institut für Technische Akustik, RWTH Aachen University, Neustrasse 50, 52066 Aachen, Germany Contributed Papers 8:00 The detailed objective acoustic parameters are presented for measurements 3aAAa1.
    [Show full text]
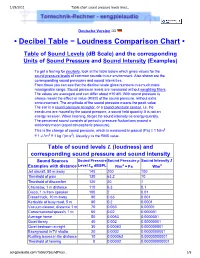
  • Table Chart Sound Pressure Levels Level Sound Pressure
    1/29/2011 Table chart sound pressure levels level… Deutsche Version • Decibel Table − Loudness Comparison Chart • Table of Sound Levels (dB Scale) and the corresponding Units of Sound Pressure and Sound Intensity (Examples) To get a feeling for decibels, look at the table below which gives values for the sound pressure levels of common sounds in our environment. Also shown are the corresponding sound pressures and sound intensities. From these you can see that the decibel scale gives numbers in a much more manageable range. Sound pressure levels are measured without weighting filters. The values are averaged and can differ about ±10 dB. With sound pressure is always meant the effective value (RMS) of the sound pressure, without extra announcement. The amplitude of the sound pressure means the peak value. The ear is a sound pressure receptor, or a sound pressure sensor, i.e. the ear-drums are moved by the sound pressure, a sound field quantity. It is not an energy receiver. When listening, forget the sound intensity as energy quantity. The perceived sound consists of periodic pressure fluctuations around a stationary mean (equal atmospheric pressure). This is the change of sound pressure, which is measured in pascal (Pa) ≡ 1 N/m2 ≡ 1 J / m3 ≡ 1 kg / (m·s2). Usually p is the RMS value. Table of sound levels L (loudness) and corresponding sound pressure and sound intensity Sound Sources Sound PressureSound Pressure p Sound Intensity I Examples with distance Level Lp dBSPL N/m2 = Pa W/m2 Jet aircraft, 50 m away 140 200 100 Threshold of pain
    [Show full text]
  • A Revised Sound Energy Theory Based on a New Formula for the Reverberation Radius in Rooms with Non-Diffuse Sound Field
    ARCHIVES OF ACOUSTICS Copyright c 2015 by PAN – IPPT Vol. 40, No. 1, pp. 33–40 (2015) DOI: 10.1515/aoa-2015-0005 A Revised Sound Energy Theory Based on a New Formula for the Reverberation Radius in Rooms with Non-Diffuse Sound Field Higini ARAU-PUCHADES(1), Umberto BERARDI(2) (1) ArauAcustica Barcelona, Spain (2) Department of Architectural Science, Ryerson University Toronto, Canada; e-mail: [email protected] (received November 9, 2014; accepted November 20, 2014 ) This paper discusses the concept of the reverberation radius, also known as critical distance, in rooms with non-uniformly distributed sound absorption. The reverberation radius is the distance from a sound source at which the direct sound level equals the reflected sound level. The currently used formulas to calculate the reverberation radius have been derived by the classic theories of Sabine or Eyring. However, these theories are only valid in perfectly diffused sound fields; thus, only when the energy density is constant throughout a room. Nevertheless, the generally used formulas for the reverberation radius have been used in any circumstance. Starting from theories for determining the reverberation time in non- diffuse sound fields, this paper firstly proposes a new formula to calculate the reverberation radius in rooms with non-uniformly distributed sound absorption. Then, a comparison between the classic formulas and the new one is performed in some rectangular rooms with non-uniformly distributed sound absorption. Finally, this paper introduces a new interpretation of the reverberation radius in non-diffuse sound fields. According to this interpretation, the time corresponding to the sound to travel a reverberation radius should be assumed as the lower limit of integration of the diffuse sound energy.
    [Show full text]
  • TRADE/CEFACT/2005/24 Recommendation No. 20
    Annex I (Normative) Units of Measure: Code elements listed by Quantity (SI and SI equivalent units) The table column titled “Level/Category” identifies the normative relevance of the unit: level 1 – normative = SI normative units, standard and commonly used multiples level 2 – normative equivalent = SI normative equivalent units (UK, US, etc.) and commonly used multiples level 3 – informative units omitted from this normative annex but found in the informative annexes, Annex II and Annex III Quantity ST Level/ Name Representation symbol Conversion factor to SI Common Category Description Code Space and Time angle (plane) | 1 radian rad m x m⁻¹ = 1 C81 | 1S milliradian mrad 10⁻³ rad C25 | 1S microradian µrad 10⁻⁶ rad B97 #| 1 degree [unit of angle] 1,745 329 x 10⁻² rad DD #| 1 minute [unit of angle] ' 2,908 882 x 10⁻⁴ rad D61 #| 1 second [unit of angle] " 4,848 137 x 10⁻⁶ rad D62 D 2 grade = gon A91 | 2 gon gon 1,570 796 x 10⁻² rad A91 solid angle | 1 steradian sr m² x m⁻² = 1 D27 length, | 1 metre m m MTR breadth | 1M decimetre dm 10⁻¹ m DMT height | 1S centimetre cm 10⁻² m CMT thickness, | 1S micrometre (micron) µm 10⁻⁶ m 4H radius, | 1S millimetre mm 10⁻³ m MMT radius of curvature | 1M hectometre hm 10² m HMT cartesian coordinates X 1S kilometre km 10³ m KTM diameter, + 1S kilometre km 10³ m KMT length of path | 1S nanometre nm 10⁻⁹ m C45 distance | 1S picometre pm 10⁻¹² m C52 TRADE/CEFACT/2005/24 Recommendation No. 20 - Units of Measure used in International Trade Page 1/40 Annex I (Normative) Units of Measure: Code elements listed
    [Show full text]
  • Comparative Representation of Sound Field Quantities
    Comparative representation of sound field quantities and sound energy quantities Assumption: German: http://www.sengpielaudio.com/VergleichendeDarstellungVonSchall.pdf Air temperarature = 20°C: (Atmospheric pressure 10,1325 Pa = 1013 hectopascal) Density of air at 20°C: = 1.204 kg / m3 (At 0°C is = 1.293 kg/m3) Speed of sound at 20°C: c = 343 m / s (At 0°C is c = 331 m/s) UdK Berlin p Sengpiel Specific acoustic impedance Z at 20°C: Z = · c = = 413 N · s / m3 (At 0°C is Z = 428 N·s/m3) 05.93 v Sound Reference sound field quantities: –5 2 –5 Reference sound pressure p0 = 2 · 10 N / m = 2 · 10 Pa (Fixed "threshold of audibility") p0 p0 –8 –8 Reference sound velocity v0 = = = 5 · 10 m / s (= 4.854 · 10 m / s) c Z0 Reference sound energy quantities: 2 p0 2 –12 2 –12 2 Reference sound intensity J0 = = Z0 · v = 10 W / m (= 0.9685 · 10 W / m ) Z0 J p v Reference sound energy density E = 0 = 00 = 3 · 10–15 W · m / s3 (= 2.824 · 10–15 J / m3) 0 c c –12 2 –12 Reference acoustic power W0 = J 0 · A = 10 W = 1 pW bei A = 1 m (= 0.9685 · 10 W) >>> Given: A plane sound wave of f = 1 kHz and the N Sound pressure p = 1 Pa = 1 = 10 bar 94 dBSPL – We use always the RMS value. m2 Calculated: c 343 Wavelength = = = 0.343 m = 34,3 cm f 1000 1 Periodic length T = = 0.001 s = 1 ms f p 1 Sound velocity v = 2 · · f · = = = 2.42 .
    [Show full text]
  • The Science and Applications of Acoustics the Science and Applications of Acoustics
    THE SCIENCE AND APPLICATIONS OF ACOUSTICS THE SCIENCE AND APPLICATIONS OF ACOUSTICS SECOND EDITION Daniel R. Raichel CUNY Graduate Center and School of Architecture, Urban Design and Landscape Design The City College of the City University of New York With 253 Illustrations Daniel R. Raichel 2727 Moore Lane Fort Collins, CO 80526 USA [email protected] Library of Congress Control Number: 2005928848 ISBN-10: 0-387-26062-5 eISBN: 0-387-30089-9 Printed on acid-free paper. ISBN-13: 978-0387-26062-4 C 2006 Springer Science+Business Media, Inc. All rights reserved. This work may not be translated or copied in whole or in part without the written permission of the publisher (Springer Science+Business Media, Inc., 233 Spring Street, New York, NY 10013, USA), except for brief excerpts in connection with reviews or scholarly analysis. Use in connection with any form of information storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology now known or hereafter developed is forbidden. The use in this publication of trade names, trademarks, service marks, and similar terms, even if they are not identified as such, is not to be taken as an expression of opinion as to whether or not they are subject to proprietary rights. Printed in the United States of America. (TB/MVY) 987654321 springeronline.com To Geri, Adam, Dina, and Madison Rose Preface The science of acoustics deals with the creation of sound, sound transmission through solids, and the effects of sound on both inert and living materials. As a mechanical effect, sound is essentially the passage of pressure fluctuations through matter as the result of vibrational forces acting on that medium.
    [Show full text]
  • Handclap for Acoustic Measurements: Optimal Application and Limitations
    acoustics Article Handclap for Acoustic Measurements: Optimal Application and Limitations Nikolaos M. Papadakis 1,2,* and Georgios E. Stavroulakis 1 1 Institute of Computational Mechanics and Optimization (Co.Mec.O), School of Production Engineering and Management, Technical University of Crete, 73100 Chania, Greece; [email protected] 2 Department of Music Technology and Acoustics, Hellenic Mediterranean University, 74100 Rethymno, Greece * Correspondence: [email protected] Received: 25 March 2020; Accepted: 7 April 2020; Published: 26 April 2020 Abstract: Handclap is a convenient and useful acoustic source. This study aimed to explore its optimal application and limitations for acoustic measurements as well for other possible utilizations. For this purpose, the following steps were performed: investigation of the optimal hand configuration for acoustic measurements and measurements at different microphone source distances and at different spaces and positions. All measurements were performed with a handclap and a dodecahedron speaker for comparison. The results indicate that the optimal hand configuration (among 11) is with the hands cupped and held at an angle due to the superior low frequency spectrum. This configuration produced usable acoustic parameter measurements in the low frequency range in common room background levels unlike other configurations. The reverberation time was measured across different spaces and positions with a deviation less than three and just a noticeable difference of the signal-to-noise ratio within or near the ISO 3382-1 limits for each corresponding octave band. Other acoustic parameters (i.e., early decay time, clarity) were measured with greater deviations for reasons discussed in the text. Finally, practical steps for measurements with a handclap as an acoustic source are suggested.
    [Show full text]
  • Sound Fields
    Ch01-H6526.tex 19/7/2007 14: 2 Page 1 Chapter 1 Sound fields 1.1 Introduction his opening chapter looks at aspects of sound fields that are particularly relevant to sound insulation; the reader will also find that it has general applications to room Tacoustics. The audible frequency range for human hearing is typically 20 to 20 000 Hz, but we generally consider the building acoustics frequency range to be defined by one-third-octave-bands from 50 to 5000 Hz. Airborne sound insulation tends to be lowest in the low-frequency range and highest in the high-frequency range. Hence significant transmission of airborne sound above 5000 Hz is not usually an issue. However, low-frequency airborne sound insulation is of partic- ular importance because domestic audio equipment is often capable of generating high levels below 100 Hz. In addition, there are issues with low-frequency impact sound insulation from footsteps and other impacts on floors. Low frequencies are also relevant to façade sound insu- lation because road traffic is often the dominant external noise source in the urban environment. Despite the importance of sound insulation in the low-frequency range it is harder to achieve the desired measurement repeatability and reproducibility. In addition, the statistical assump- tions used in some measurements and prediction models are no longer valid. There are some situations such as in recording studios or industrial buildings where it is necessary to consider frequencies below 50 Hz and/or above 5000 Hz. In most cases it should be clear from the text what will need to be considered at frequencies outside the building acoustics frequency range.
    [Show full text]
  • Generalized Acoustic Energy Density and Its Applications
    Brigham Young University BYU ScholarsArchive Theses and Dissertations 2010-09-30 Generalized Acoustic Energy Density and Its Applications Buye Xu Brigham Young University - Provo Follow this and additional works at: https://scholarsarchive.byu.edu/etd Part of the Astrophysics and Astronomy Commons, and the Physics Commons BYU ScholarsArchive Citation Xu, Buye, "Generalized Acoustic Energy Density and Its Applications" (2010). Theses and Dissertations. 2339. https://scholarsarchive.byu.edu/etd/2339 This Dissertation is brought to you for free and open access by BYU ScholarsArchive. It has been accepted for inclusion in Theses and Dissertations by an authorized administrator of BYU ScholarsArchive. For more information, please contact [email protected], [email protected]. Generalized Acoustic Energy Density and Its Applications Buye Xu A dissertation submitted to the faculty of Brigham Young University in partial fulfillment of the requirements for the degree of Doctor of Philosophy Scott. D. Sommerfeldt, Chair Timothy W. Leishman Jonathon D. Blotter Kent L. Gee G. Bruce Schaalje Department of Physics and Astronomy Brigham Young University December 2010 Copyright c 2010 Buye Xu All Rights Reserved ABSTRACT Generalized Acoustic Energy Density and Its Applications Buye Xu Department of Physics and Astronomy Doctor of Philosophy The properties of acoustic kinetic energy density and total energy density of sound fields in lightly damped enclosures have been explored thoroughly in the literature. Their increased spatial uniformity makes them more favorable measurement quantities for various applica- tions than acoustic potential energy density (or squared pressure), which is most often used. In this dissertation, a new acoustic energy quantity, the generalized acoustic energy density (GED), will be introduced.
    [Show full text]