DOCSLIB.ORG

Universidade Técnica De Lisboa Instituto Superior

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Universidade Técnica De Lisboa Instituto Superior UNIVERSIDADE TÉCNICA DE LISBOA INSTITUTO SUPERIOR TÉCNICO ACOUSTIC MODELLING FOR VIRTUAL SPACES Diogo Gonçalo Franco Falcão Osório de Alarcão (Licenciado) Dissertação para obtenção do Grau de Doutor em Engenharia Electrotécnica e de Computadores Orientador: Doutor José Luís Bento Coelho Júri Presidente: Reitor da Universidade Técnica de Lisboa Vogais: Doutor Luís Manuel Braga da Costa Campos Doutor Jorge Viçoso Patrício Doutor José Luís Bento Coelho Doutor João Manuel Domingues Perdigão Doutor Afonso Manuel dos Santos Barbosa Novembro 2005 UNIVERSIDADE TÉCNICA DE LISBOA INSTITUTO SUPERIOR TÉCNICO ACOUSTIC MODELLING FOR VIRTUAL SPACES Diogo Gonçalo Franco Falcão Osório de Alarcão (Licenciado) Dissertação para obtenção do Grau de Doutor em Engenharia Electrotécnica e de Computadores Orientador: Doutor José Luís Bento Coelho Júri Presidente: Reitor da Universidade Técnica de Lisboa Vogais: Doutor Luís Manuel Braga da Costa Campos Doutor Jorge Viçoso Patrício Doutor José Luís Bento Coelho Doutor João Manuel Domingues Perdigão Doutor Afonso Manuel dos Santos Barbosa Novembro 2005 ii To my son Rodrigo and to my daughter Inês iii Abstract This thesis presents a new model for the sound energy propagation inside enclosed spaces. The new model is developed starting from the physical first principles and from rigorous mathematical definitions. The theoretical foundation allows the rigorous definition of the energy-based quantities used for describing sound energy propagation inside enclosures and the definition of a general energy balance equation for sound particles, applicable to any room. In addition, new theoretical tools for the study of sound energy fields in rooms are introduced, which are based on the language of functional analysis. The governing equations are thus expressed in terms of linear operators with very convenient properties, which are mathematically detailed. In addition, a new combined method that solves the derived equations is presented. This new combined method uses an extended mirror image source method solving for the propagation of the specularly reflected energy components inside enclosures, and a time-dependent hierarchical radiosity method solving for the propagation of the diffusely reflected energy components. New algorithmic refinements are introduced in the computer implementation of this combined method. Finally, it is shown that the new proposed method is fast, flexible and accurate enough to be applied as an alternative method for room acoustics simulation. Key words: room acoustics, sound particles, linear integral operators, diffuse and specular reflections, extended image source method, time-dependent hierarchical radiosity. iv Resumo A presente Tese descreve um novo modelo da propagação da energia sonora em recintos fechados. O novo modelo é desenvolvido a partir de primeiros princípios físicos e de definições matemáticas rigorosas. As fundações teóricas obtidas permitem definir de forma rigorosa as quantidades energéticas usadas na descrição da propagação de energia sonora dentro de salas bem como a definição de uma equação geral de balanço de energia para partículas sonoras, aplicável a uma sala qualquer. São introduzidas novas ferramentas teóricas para o estudo de campos de energia sonora em salas, baseadas na linguagem da análise funcional. As equação que governam a propagação de energia sonora são pois expressas em termos de operadores lineares com propriedades convenientes. Adicionalmente, é apresentado um novo método combinado para a resolução das equações derivadas. Este método combinado utiliza o método das imagens estendido para a solução da propagação das componentes reflectidas especularmente e o método de radiosidade hiérarquica, dependente do tempo, para obter a solução da propagação das componentes reflectidas difusamente. São ainda apresentados vários aperfeiçoamentos utilizados nos algoritmos implementados do método combinado. Finalmente, mostra-se que o novo método combinado é de computação rápida, fléxivel e suficientemente preciso estabelecendo-se num método alternativo para a simulação de acústica de salas. Palavras chave: acústica de salas, partículas sonoras, operadores integrais lineares, reflexões difusas e especulares, método das fontes imagem estendido, radiosidade hierárquica dependente do tempo. v ACKNOWLEDGMENTS I would like to sincerely thank my advisor Professor J. L. Bento Coelho for giving me the opportunity of conducting this work under his supervison. I thank him for the continuous encouragement and unhesitating support during this endeavour and for the the help in the preparation of this thesis. I must also thank my family, specially my wife Marta, for her love, understanding and patience at every step along the way. A very special thanks to my parents, especially to my mother, who was the first person that pressed me to start such a difficult task, giving me confidence and encouragement. Finally, to my young son and daughter, I thank them for their great patience when, many times, their father was wholly absorbed in his research and could not give them all the attention they deserve. This work was partially financially supported by FCT – Portuguese Foundation for Science and Technology under the III QCA of the EU. v i TABLE OF CONTENTS Chapter 1 – Introduction................................................................................................................................... 1 Chapter 2 – Basic Theory Concepts................................................................................................................ 7 2.1 Introduction............................................................................................................................. 7 2.2 Physical Descriptors............................................................................................................... 8 2.2.1 Characterisation of Acoustic Disturbances.............................................................. 9 2.2.2 The Wave Equation.................................................................................................... 11 2.2.3 Intensity and Energy Density ................................................................................... 16 2.2.4 Harmonic and Non-harmonic Sound Waves........................................................ 20 2.3 Sound Sources and Receivers............................................................................................. 22 2.4 Sound Radiation.................................................................................................................... 24 2.5 Sound Receivers.................................................................................................................... 25 2.6 Propagation of Sound Waves............................................................................................. 26 2.6.1 The Sound Field in Front of a Wall......................................................................... 27 2.6.2 Diffraction of Sound Waves ..................................................................................... 39 2.6.3 The Attenuation of Sound in Air............................................................................. 41 2.6.4 Sound Absorbers......................................................................................................... 43 2.6.4.1 Membrane Absorbers..........................................................................................43 2.6.4.2 Porous Absorbers ................................................................................................45 2.6.4.3 Resonant Absorbers ............................................................................................46 2.6.4.4 People and Furniture...........................................................................................47 2.7 Sound Perception ................................................................................................................. 47 2.7.1 Fundamental Properties of the Human Ear .......................................................... 48 2.7.1.1 Intensity Perception of the Auditory System. Thresholds. ..........................49 2.7.1.2 Equal Loudness Contours..................................................................................50 2.7.1.3 Frequency Perception of the Auditory System...............................................51 2.7.1.4 Critical Bandwidths and Masking......................................................................52 2.7.1.5 Time Perception...................................................................................................53 2.7.1.6 Spatial Sound Perception....................................................................................53 Chapter 3 – Sound Fields in Enclosures....................................................................................................... 57 3.1 Introduction........................................................................................................................... 57 3.2 The Wave Equation and Boundary Conditions.............................................................. 58 3.3 Natural Modes for the Rectangular Room ...................................................................... 59 3.4 Steady-state and Transient Sound Fields inside Enclosures......................................... 65 3.5 Reverberation Time..............................................................................................................69 3.5.1 Time Distribution of Reflections............................................................................
Load more

Recommended publications
  • On the Use of Boundary Integral Equations and Linear Operators in Room Acoustics
    Guimarães - Portugal paper ID: 169 /p.1 On the Use of Boundary Integral Equations and Linear Operators in Room Acoustics D. Alarcão and J. L. Bento Coelho CAPS – Instituto Superior Técnico, Av. Rovisco Pais, P-1049-001 Lisbon, Portugal, [email protected] RESUMO: Este artigo introduz alguns conceitos de base sobre equações integrais e mostra a sua aplicação na determinação da propagação de energia acústica em recintos fechados. Mostra-se que as equações integrais resultantes podem ser formuladas na linguagem dos operadores lineares, daí resultando uma notação simplificada em que as propriedades algébricas das equações que determinam a propagação da energia são mais facilmente caracterizadas. São apresentados alguns métodos gerais de resolução de equações integrais tal como métodos aproximados e métodos de bases vectoriais finitas. Apresentam-se, ainda, as definições necessárias envolvidas na descrição de campos de energia acústica, que servem de ponto de partida à aplicação das técnicas apresentadas. ABSTRACT: This paper introduces some basic concepts of boundary integral equations and their application for the determination of the propagation of sound energy inside enclosures. Linear operators are shown to provide a simplified notation and to emphasize the algebraic properties of the resulting integral equations. Some general methods of solving linear operator and integral equations are reviewed and discussed, such as approximation methods and finite basis methods. In addition, some of the necessary definitions involved in describing acoustic energy fields for applying these techniques in the field of room acoustics prediction are presented. 1. INTRODUCTION Energy based methods offer an interesting and valid alternative mid and high frequency technique to classical predictive methods such as FEM, BEM and others.
    [Show full text]
  • Industrial Noise Control and Acoustics
    Industrial Noise Control and Acoustics Randall F. Barron Louisiana Tech University Ruston, Louisiana, U.S.A. Marcel Dekker, Inc. New York • Basel Copyright © 2001 by Marcel Dekker, Inc. All Rights Reserved. Copyright © 2003 Marcel Dekker, Inc. LibraryofCongressCataloging-in-PublicationData AcatalogrecordforthisbookisavailablefromtheLibraryofCongress. ISBN:0-8247-0701-X Thisbookisprintedonacid-freepaper. Headquarters MarcelDekker,Inc. 270MadisonAvenue,NewYork,NY10016 tel:212-696-9000;fax:212-685-4540 EasternHemisphereDistribution MarcelDekkerAG Hutgasse4,Postfach812,CH-4001Basel,Switzerland tel:41-61-260-6300;fax:41-61-260-6333 WorldWideWeb http://www.dekker.com The publisher offers discounts on this book when ordered in bulk quantities, For more information, write to Special Sales/Professional Marketing at the headquarters address above. Copyright # 2003 by Marcel Dekker, Inc. All Rights Reserved. Neither this book nor any part may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, microfilming, and recording, or by any information storage retrieval system, without permission in writing from the publisher. Current printing (last digit): 10987654321 PRINTED IN THE UNITED STATES OF AMERICA Copyright © 2003 Marcel Dekker, Inc. Preface Since the Walsh-Healy Act of 1969 was amended to include restrictions on the noise exposure of workers, there has been much interest and motivation in industry to reduce noise emitted by machinery. In addition to concerns about air and water pollution by contaminants, efforts have also been direc- ted toward control of environmental noise pollution. In response to these stimuli, faculty at many engineering schools have developed and introduced courses in noise control, usually at the senior design level. It is generally much more effective to design ‘‘quietness’’ into a product than to try to ‘‘fix’’ the noise problem in the field after the product has been put on the market.
    [Show full text]
  • Definition and Measurement of Sound Energy Level of a Transient Sound Source
    J. Acoust. Soc. Jpn. (E) 8, 6 (1987) Definition and measurement of sound energy level of a transient sound source Hideki Tachibana,* Hiroo Yano,* and Koichi Yoshihisa** *Institute of Industrial Science , University of Tokyo, 7-22-1, Roppongi, Minato-ku, Tokyo, 106 Japan **Faculty of Science and Technology, Meijo University, 1-501, Shiogamaguti, Tenpaku-ku, Nagoya, 468 Japan (Received 1 May 1987) Concerning stationary sound sources, sound power level which describes the sound power radiated by a sound source is clearly defined. For its measuring methods, the sound pressure methods using free field, hemi-free field and diffuse field have been established, and they have been standardized in the international and national stan- dards. Further, the method of sound power measurement using the sound intensity technique has become popular. On the other hand, concerning transient sound sources such as impulsive and intermittent sound sources, the way of describing and measuring their acoustic outputs has not been established. In this paper, therefore, "sound energy level" which represents the total sound energy radiated by a single event of a transient sound source is first defined as contrasted with the sound power level. Subsequently, its measuring methods by two kinds of sound pressure method and sound intensity method are investigated theoretically and experimentally on referring to the methods of sound power level measurement. PACS number : 43. 50. Cb, 43. 50. Pn, 43. 50. Yw sources, the way of describing and measuring their 1. INTRODUCTION acoustic outputs has not been established. In noise control problems, it is essential to obtain In this paper, "sound energy level" which repre- the information regarding the noise sources.
    [Show full text]
  • AMATH 731: Applied Functional Analysis Lecture Notes
    AMATH 731: Applied Functional Analysis Lecture Notes Sumeet Khatri November 24, 2014 Table of Contents List of Tables ................................................... v List of Theorems ................................................ ix List of Definitions ................................................ xii Preface ....................................................... xiii 1 Review of Real Analysis .......................................... 1 1.1 Convergence and Cauchy Sequences...............................1 1.2 Convergence of Sequences and Cauchy Sequences.......................1 2 Measure Theory ............................................... 2 2.1 The Concept of Measurability...................................3 2.1.1 Simple Functions...................................... 10 2.2 Elementary Properties of Measures................................ 11 2.2.1 Arithmetic in [0, ] .................................... 12 1 2.3 Integration of Positive Functions.................................. 13 2.4 Integration of Complex Functions................................. 14 2.5 Sets of Measure Zero......................................... 14 2.6 Positive Borel Measures....................................... 14 2.6.1 Vector Spaces and Topological Preliminaries...................... 14 2.6.2 The Riesz Representation Theorem........................... 14 2.6.3 Regularity Properties of Borel Measures........................ 14 2.6.4 Lesbesgue Measure..................................... 14 2.6.5 Continuity Properties of Measurable Functions...................
    [Show full text]
  • Derivation of the Sabine Equation: Conservation of Energy
    UIUC Physics 406 Acoustical Physics of Music Derivation of the Sabine Equation: Conservation of Energy Consider a large room of volume V = HWL (m3) with perfectly reflecting walls, filled with a uniform, steady-state (i.e. equilibrium) acoustic energy density wrtfa ,, at given frequency f (Hz) within the volume V of the room. Uniform energy density means that a given time t: 3 waa r,, t f w t , f constant (SI units: Joules/m ). The large room also has a small opening of area A (m2) in it, as shown in the figure below: H V A I rt,, f ac nAˆˆ, An W L In the steady-state, the rate of acoustical energy Wa input e.g. by a point sound source within the large room equals the rate at which acoustical energy is “leaking” out of the room through the hole of area A, i.e. the acoustical power input by the sound source in the room into the room = the acoustical power leaving the room through the hole of area A. In this idealized model of a room with perfectly reflecting walls, the hole of area A thus represents absorption of sound in a real room with finite reflectivity walls, i.e. walls that have some absorption associated with them. Suppose at time t = 0 the sound source in the room {located far from the hole} is turned off. Since the sound energy density is uniform in the room, the sound energy contained in the room Wtf,,,, wrtfdrwtf 33 drwtfV , will thus decrease with time, since aaVV a a acoustical energy is (slowly) leaking out of the room through the opening of area A.
    [Show full text]
  • Measurement of Total Sound Energy Density in Enclosures at Low Frequencies Abstract of Paper
    View metadata,Downloaded citation and from similar orbit.dtu.dk papers on:at core.ac.uk Dec 17, 2017 brought to you by CORE provided by Online Research Database In Technology Measurement of total sound energy density in enclosures at low frequencies Abstract of paper Jacobsen, Finn Published in: Acoustical Society of America. Journal Link to article, DOI: 10.1121/1.2934233 Publication date: 2008 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Jacobsen, F. (2008). Measurement of total sound energy density in enclosures at low frequencies: Abstract of paper. Acoustical Society of America. Journal, 123(5), 3439. DOI: 10.1121/1.2934233 General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. WEDNESDAY MORNING, 2 JULY 2008 ROOM 242B, 8:00 A.M. TO 12:40 P.M. Session 3aAAa Architectural Acoustics: Case Studies and Design Approaches I Bryon Harrison, Cochair 124 South Boulevard, Oak Park, IL, 60302 Witew Jugo, Cochair Institut für Technische Akustik, RWTH Aachen University, Neustrasse 50, 52066 Aachen, Germany Contributed Papers 8:00 The detailed objective acoustic parameters are presented for measurements 3aAAa1.
    [Show full text]
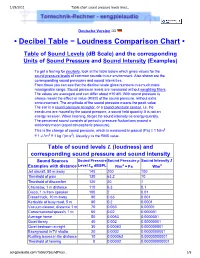
  • Table Chart Sound Pressure Levels Level Sound Pressure
    1/29/2011 Table chart sound pressure levels level… Deutsche Version • Decibel Table − Loudness Comparison Chart • Table of Sound Levels (dB Scale) and the corresponding Units of Sound Pressure and Sound Intensity (Examples) To get a feeling for decibels, look at the table below which gives values for the sound pressure levels of common sounds in our environment. Also shown are the corresponding sound pressures and sound intensities. From these you can see that the decibel scale gives numbers in a much more manageable range. Sound pressure levels are measured without weighting filters. The values are averaged and can differ about ±10 dB. With sound pressure is always meant the effective value (RMS) of the sound pressure, without extra announcement. The amplitude of the sound pressure means the peak value. The ear is a sound pressure receptor, or a sound pressure sensor, i.e. the ear-drums are moved by the sound pressure, a sound field quantity. It is not an energy receiver. When listening, forget the sound intensity as energy quantity. The perceived sound consists of periodic pressure fluctuations around a stationary mean (equal atmospheric pressure). This is the change of sound pressure, which is measured in pascal (Pa) ≡ 1 N/m2 ≡ 1 J / m3 ≡ 1 kg / (m·s2). Usually p is the RMS value. Table of sound levels L (loudness) and corresponding sound pressure and sound intensity Sound Sources Sound PressureSound Pressure p Sound Intensity I Examples with distance Level Lp dBSPL N/m2 = Pa W/m2 Jet aircraft, 50 m away 140 200 100 Threshold of pain
    [Show full text]
  • Arxiv:1709.09646V1 [Math.FA] 27 Sep 2017 Mensional Aahspace Banach Us-Opeetdin Quasi-Complemented Iesoa Aahspace Banach Dimensional Basis? Schauder a with Quotient 2
    ON THE SEPARABLE QUOTIENT PROBLEM FOR BANACH SPACES J. C. FERRANDO, J. KA¸KOL, M. LOPEZ-PELLICER´ AND W. SLIWA´ To the memory of our Friend Professor Pawe l Doma´nski Abstract. While the classic separable quotient problem remains open, we survey gen- eral results related to this problem and examine the existence of a particular infinite- dimensional separable quotient in some Banach spaces of vector-valued functions, linear operators and vector measures. Most of the results presented are consequence of known facts, some of them relative to the presence of complemented copies of the classic sequence spaces c0 and ℓp, for 1 ≤ p ≤ ∞. Also recent results of Argyros, Dodos, Kanellopoulos [1] and Sliwa´ [66] are provided. This makes our presentation supplementary to a previous survey (1997) due to Mujica. 1. Introduction One of unsolved problems of Functional Analysis (posed by S. Mazur in 1932) asks: Problem 1. Does any infinite-dimensional Banach space have a separable (infinite di- mensional) quotient? An easy application of the open mapping theorem shows that an infinite dimensional Banach space X has a separable quotient if and only if X is mapped on a separable Banach space under a continuous linear map. Seems that the first comments about Problem 1 are mentioned in [46] and [55]. It is already well known that all reflexive, or even all infinite-dimensional weakly compactly generated Banach spaces (WCG for short), have separable quotients. In [38, Theorem IV.1(i)] Johnson and Rosenthal proved that every infinite dimensional separable Banach arXiv:1709.09646v1 [math.FA] 27 Sep 2017 space admits a quotient with a Schauder basis.
    [Show full text]
  • Continuity of Convolution of Test Functions on Lie Groups
    Canad. J. Math. Vol. 66 (1), 2014 pp. 102–140 http://dx.doi.org/10.4153/CJM-2012-035-6 c Canadian Mathematical Society 2012 Continuity of Convolution of Test Functions on Lie Groups Lidia Birth and Helge Glockner¨ 1 1 1 Abstract. For a Lie group G, we show that the map Cc (G) × Cc (G) ! Cc (G), (γ; η) 7! γ ∗ η, taking a pair of test functions to their convolution, is continuous if and only if G is σ-compact. More generally, consider r; s; t 2 N0 [ f1g with t ≤ r + s, locally convex spaces E1, E2 and a continuous r s bilinear map b: E1 × E2 ! F to a complete locally convex space F. Let β : Cc (G; E1) × Cc(G; E2) ! t Cc(G; F), (γ; η) 7! γ ∗b η be the associated convolution map. The main result is a characterization of those (G; r; s; t; b) for which β is continuous. Convolution of compactly supported continuous functions on a locally compact group is also discussed as well as convolution of compactly supported L1-functions and convolution of compactly supported Radon measures. 1 Introduction and Statement of Results It has been known since the beginnings of distribution theory that the bilinear convo- 1 n 1 n 1 n lution map β : Cc (R )×Cc (R ) ! Cc (R ), (γ; η) 7! γ ∗η (and even convolution 1 n 0 1 n 1 n C (R ) × Cc (R ) ! Cc (R )) is hypocontinuous [39, p. 167]. However, a proof for continuity of β was published only recently [29, Proposition 2.3].
    [Show full text]
  • Random Linear Functionals
    RANDOM LINEAR FUNCTIONALS BY R. M. DUDLEYS) Let S be a real linear space (=vector space). Let Sa be the linear space of all linear functionals on S (not just continuous ones even if S is topological). Let 86{Sa, S) or @{S) denote the smallest a-algebra of subsets of Sa such that the evaluation x -> x(s) is measurable for each s e S. We define a random linear functional (r.l.f.) over S as a probability measure P on &(S), or more formally as the pair (Sa, P). In the cases we consider, S is generally infinite-dimensional, and in some ways Sa is too large for convenient handling. Various alternate characterizations of r.l.f.'s are useful and will be discussed in §1 below. If 7 is a topological linear space let 7" be the topological dual space of all con- tinuous linear functions on T. If 7" = S, then a random linear functional over S defines a " weak distribution " on 7 in the sense of I. E. Segal [23]. See the discussion of "semimeasures" in §1 below for the relevant construction. A central question about an r.l.f. (Sa, P), supposing S is a topological linear space, is whether P gives outer measure 1 to S'. Then we call the r.l.f. canonical, and as is well known P can be restricted to S' suitably (cf. 2.3 below). For simplicity, suppose that for each s e S, j x(s)2 dP(x) <oo. Let C(s)(x) = x(s).
    [Show full text]
  • On Limits of Sequences of Resolvent Kernels for Subkernels
    ON LIMITS OF SEQUENCES OF RESOLVENT KERNELS FOR SUBKERNELS IGOR M. NOVITSKII Abstract. In this paper, we approximate to continuous bi-Carleman kernels vanishing at in- finity by sequences of their subkernels of Hilbert-Schmidt type and try to construct the resolvent kernels for these kernels as limits of sequences of the resolvent kernels for the approximating subkernels. 1. Introduction In the general theory of integral equations of the second kind in L2 = L2(R), i.e., equations of the form f(s) λ T (s,t)f(t) dt = g(s) for almost every s R, (1.1) − R ∈ Z it is customary to call an integral kernel T |λ a resolvent kernel for T at λ if the integral operator 2 −1 it induces on L is the Fredholm resolvent T|λ := T (I λT ) of the integral operator T , which 2 − is induced on L by the kernel T . Once the resolvent kernel T |λ has been constructed, one can express the L2-solution f to equation (1.1) in a direct and simple fashion as f(s)= g(s)+ λ T |λ(s,t)g(t) dt for almost every s R, R ∈ Z regardless of the particular choice of the function g of L2. Here it should be noted that, in general, the property of being an integral operator is not shared by Fredholm resolvents of integral operators, and there is even an example, given in [17] (see also [18, Section 5, Theorem 8]), of an integral operator having the property that at each non-zero regular value of the parameter λ, its Fredholm resolvent is not an integral operator.
    [Show full text]
  • Essential Self-Adjointness of the Symplectic Dirac Operators
    Essential Self-Adjointness of the Symplectic Dirac Operators by A. Nita B.A., University of California, Irvine, 2007 M.A., University of Colorado, Boulder, 2010 A thesis submitted to the Faculty of the Graduate School of the University of Colorado in partial fulfillment of the requirements for the degree of Doctor of Philosophy Department of Mathematics 2016 This thesis entitled: Essential Self-Adjointness of the Symplectic Dirac Operators written by A. Nita has been approved for the Department of Mathematics Prof. Alexander Gorokhovsky Prof. Carla Farsi Date The final copy of this thesis has been examined by the signatories, and we find that both the content and the form meet acceptable presentation standards of scholarly work in the above mentioned discipline. iii Nita, A. (Ph.D., Mathematics) Essential Self-Adjointness of the Symplectic Dirac Operators Thesis directed by Prof. Alexander Gorokhovsky The main problem we consider in this thesis is the essential self-adjointness of the symplectic Dirac operators D and D~ constructed by Katharina Habermann in the mid 1990s. Her construc- tions run parallel to those of the well-known Riemannian Dirac operators, and show that in the symplectic setting many of the same properties hold. For example, the symplectic Dirac operators are also unbounded and symmetric, as in the Riemannian case, with one important difference: the bundle of symplectic spinors is now infinite-dimensional, and in fact a Hilbert bundle. This infinite dimensionality makes the classical proofs of essential self-adjointness fail at a crucial step, 2 n namely in local coordinates the coefficients are now seen to be unbounded operators on L (R ).
    [Show full text]