DOCSLIB.ORG

Pure and Applied Mathematics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Pure and Applied Mathematics Pure and Applied Mathematics ➤ ALGEBRa / COMBINATORICS ➤ LOGIc / SET THEORY ➤ NUMBER THEORY ➤ GEOMETRY / TOPOLOGY ➤ GROUPS AND REPRESENTATION THEORY ➤ ANALYSIS / OPERATOR THEORY ➤ PROBABILITY / STATISTICS / NUMERIcaL METHODS ➤ MaTHEMATIcaL PHYSICS / PHYSICS ➤ DIFFERENTIAL EQUATIONS / DYNAMIcaL SYSTEMS ➤ APPLIED MaTHEMATICS ➤ GENERAL INTEREST / REFERENCE / MaTH EDUcaTION www.birkhauser.com ALGEBRA / COMBINATORICS Cornerstones is a new Birkhäuser series that is comprised of textbooks focusing on “what students need to know” and Advanced Algebra “what faculty should teach” in various selected topics in pure ANTHONY W. KNAPP, State University of New York, Stony Brook, NY mathematics and related subjects. Basic Algebra and Advanced Algebra systematically develop Series Editors: concepts and tools in algebra that are vital to every mathematician, whether pure or applied, aspiring or established. Together the two CHARLES L. EPSTEIN, University of Pennsylvania, Philadelphia, PA books give the reader a global view of algebra and its role in math- STEVEN G. KRANTZ, Washington University, St. Louis, MO ematics as a whole. Basic Algebra Key Topics and Features of Advanced Algebra: ANTHONY W. KNAPP, State University of • Topics build upon the linear algebra, group theory, factoriza- New York at Stony Brook, NY tions of ideals, structure of fields, Galois theory, and elementary theory of modules as developed in Basic Algebra Basic Algebra and Advanced Algebra systematically develop concepts and tools • Chapters on modern algebra treat various topics in commuta- in algebra that are vital to every mathema- tive and noncommutative algebra and povide introductions to tician, whether pure or applied,, aspiring the theory of associative algebras, homological algebras, alge- or established. Together, the two books braic number theory, and algebraic geometry give the reader a global view of algebra • Continues to carry on the three prominent themes recurring in and its role in mathematics as a whole. Basic Algebra: the anaology between integers and polynomials in one variable over a field, the interplay between linear algebra and group theory, and the relationship between number theory Key Topics and Features of Basic Algebra: and geometry • Linear algebra and group theory build on each other continually • Many examples and hundreds of problems are included, along • Chapters on modern algebra treat groups, rings, fields, modules, with hints or complete solutions for most of the problems and Galois groups with emphasis on methods of computation • The exposition proceeds from the particular to the general, throughout often providing examples well before a theory that incorporates • Three prominent themes recur and blend together at times: the them; it includes blocks of problems that introduce additional analogy between integers and polynomials in one variable over topics and applications for futher study a field, the interplay between linear algebra and group theory, Advanced Algebra presents its subject matter in a forward-look- and the relationship between number theory and geometry ing way that takes into accoutn the historical development of the • Many examples and hundreds of problems are included, along subject. It is suitable as a text in a two-semester advanced under- with a separate 90-page section giving hints or complete solu- graduated or first-year graduate sequence in algebra, possibly sup- tions for most of the problems plemented for a graduate sequence by some material from Basic • The exposition proceeds from the particular to the general, of- Algebra. It requires of the reader only familiarity with matrix algebra, ten providing examples well before a theory that incorporates an understanding of the geometry and reduction of linear equa- them; includes blocks of problems that introduce additional tions, and an acquantance with proofs. topics and applications for future study Contents: Preface. • Guide for the Reader. • Transition to Modern • Applications to science and engineering (e.g., the fast Fourier Number Theory. • Wedderburn-Artin Ring Theory. • Brauer Group. transform, the theory of error-correcting codes, the use of the • Homological Algebra. • Three Theorems in Algebraic Number Theory. Jordan canonical form in solving linear systems of ordinary dif- • Reinterpretation with Adeles and Ideles. • Infinite Field Extensions. ferential equations, and constructions of interest in mathemati- • Background for Algebraic Geometry. • The Number Theory of cal physics) appear in sequences of problems Algebraic Curves. • Methods of Algebraic Geometry. • Index 2007 / APPROX. 650 PP., 10 ILLUS. / HARDCOVER / $69.95 Basic Algebra presents the subject matter in a forward-looking way ISBN_13 978-0-8176-4533-5 that takes into account its historical development. It is suitable as a ISBN_10 0-8176-4533-0 text in a two-semester advanced undergraduate or first-year graduate CORNERSTONES sequence in algebra, possibly supplemented by some material from Advanced Algebra at the graduate level. It requires of the reader only familiarity with matrix algebra, an understanding of the geometry and reduction of linear equations, and an acquaintance with proofs. Set of Basic Algebra Contents: Preface. • Guide for the Reader • Preliminaries about the and Advanced Algebra Integers, Polynomials, and Matrices. • Vector Spaces over Q R and C. 2007/$89.95 (TENT.) ISBN_13 978-0-8176-4533-5 • Inner-Product Spaces. • Group and Group Actions. • Theory of a Single ISBN_10 0-8176-4533-0 Linear Transformation. • Multilinear Algebra. • Advanced Group Theory. CORNERSTONES • Commutative Rings and Their Modules. • Fields and Galois Theory. • Modules over Noncommutative Rings. • Appendix. • Index See pages 28 and 30 for additional titles in the Cornerstones Series 2006 / 718 PP., 42 ILLUS. / HARDCOVER / $69.95 ISBN_13 978-0-8176-3248-9 ISBN_10 0-8176-3248-4 CORNERSTONES Order By Phone: 1-800-777-4643 • Fax: 01-348-4505 • Or Online: www.birkhauser.com ALGEBRA / COMBINATORICS Representation Theory and Artinian Modules Over Group Automorphic Forms Rings TOSHIYUKI KOBAYASHI, Kyoto University, RIMS, Kyoto, Japan; LEONID KURDacHENKO, Dnipropetrovsk National University, Ukraine; WILFRIED ScHMID, Harvard University, Cambridge, MA; JAVIER OTAL, University of Zaragoza, Spain; JAE-HYUN YaNG, Inha University, Incheon, Korea (Eds.) IGOR Ya. SUBBOTIN, National University, Los Angeles, CA This volume uses a unified approach to representation theory and This book highlights important developments on artinian modules automorphic forms. The invited papers, written by leading mathema- over group rings of generalized nilpotent groups. Along with tradi- ticians in related fields, track recent progress in the ever expanding tional topics such as direct decompositions of artinian modules, fields of representation theory and automorphic forms, and their as- criteria of complementability for some important modules, and cri- sociation with number theory and differential geometry. teria of semisimplicity of artinian modules, it also focuses on recent Contributors: T. Ikeda, T. Kobayashi, S. Miller, D. Ramakrishnan, advanced results. W. Schmid, F. Shahidi, K. Yoshikawa The theory of modules over groups has its own specific character 2007 / APPROX. 310 PP., 10 ILLUS. / HARDCOVER / $89.95 (TENT.) that plays an imperative role here and, for example, allows for a ISBN_13 978-0-8176-4505-2 significant generalization of the classical Maschke Theorem on ISBN_10 0-8176-4505-5 PROGRESS IN MATHEMATICS, VOL. 55 some classes of infinite groups. Conversely, it leads to establishing direct decompositions of artinian modules related to important natural formations, which, in turn, find very efficient applications in infinite groups. Schubert Varieties As self-contained as possible, this book will be useful for students as V. LakSHMIBAI, Northeastern University, Boston, MA; well as for experts in group theory, ring theory, and module theory. PETER LITTELMANN, Bergische Universität, Wuppertal, Germany; 2007 / APPROX. 264 PP. / SOFTCOVER / $49.95 (TENT.) C.S. SESHADRI, Chennai Mathematical Institute, Chennai, India ISBN_13 978-3-7643-7764-9 ISBN_10 3-7643-7764-X Over the past two decades, and more intensely in recent years, the FRONTIERS IN MATHEMATICS algebro-geometric study of Schubert Varieties has had considerable impact on the theory of algebraic groups. One of the most interest- ing developments in the theory has been the construction of natural bases of representations of the full linear group, the orthogonal The Geometry of the group, and the symplectic group. This construction gives character Word Problem for Finitely formulas of these representations which are quite different in spirit from the famous character formulas of H. Weyl. In fact, they connect Generated Groups to monomial theory and the work of Hodge which was done more NOEL BRADY, University of Oklahoma, Norman, OK; than fifty years ago, and to the very recent developments in path HaMISH SHORT, Université de Provence, Marseille, France; models, Frobenius splittings, and quantum groups. TIM RILEY, Cornell University, Ithaca, NY Written by three of the world’s leading mathematicians in algebraic The origins of the word problem in group theory are decidability geometry, group theory, and combinatorics, this excellent self- con- and complexity, but through the vision of M. Gromov and the lan- tained exposition on Schubert Varieties unfolds systematically, from guage of filling functions, the topic now impacts the world of large- relevant introductory
Load more

Recommended publications
  • Journal of Geometry and Physics
    JOURNAL OF GEOMETRY AND PHYSICS AUTHOR INFORMATION PACK TABLE OF CONTENTS XXX . • Description p.1 • Audience p.2 • Impact Factor p.2 • Abstracting and Indexing p.2 • Editorial Board p.2 • Guide for Authors p.4 ISSN: 0393-0440 DESCRIPTION . The Journal of Geometry and Physics is an International Journal in Mathematical Physics. The Journal stimulates the interaction between geometry and physics by publishing primary research, feature and review articles which are of common interest to practitioners in both fields. The Journal of Geometry and Physics now also accepts Letters, allowing for rapid dissemination of outstanding results in the field of geometry and physics. Letters should not exceed a maximum of five printed journal pages (or contain a maximum of 5000 words) and should contain novel, cutting edge results that are of broad interest to the mathematical physics community. Only Letters which are expected to make a significant addition to the literature in the field will be considered. The Journal covers the following areas of research: Methods of: • Algebraic and Differential Topology • Algebraic Geometry • Real and Complex Differential Geometry • Riemannian Manifolds • Symplectic Geometry • Global Analysis, Analysis on Manifolds • Geometric Theory of Differential Equations • Geometric Control Theory • Lie Groups and Lie Algebras • Supermanifolds and Supergroups • Discrete Geometry • Spinors and Twistors Applications to: • Strings and Superstrings • Noncommutative Topology and Geometry • Quantum Groups • Geometric Methods in Statistics and Probability • Geometry Approaches to Thermodynamics • Classical and Quantum Dynamical Systems • Classical and Quantum Integrable Systems AUTHOR INFORMATION PACK 2 Oct 2021 www.elsevier.com/locate/geomphys 1 • Classical and Quantum Mechanics • Classical and Quantum Field Theory • General Relativity • Quantum Information • Quantum Gravity Benefits to authors We also provide many author benefits, such as free PDFs, a liberal copyright policy, special discounts on Elsevier publications and much more.
    [Show full text]
  • Notices of the American Mathematical Society
    ISSN 0002-9920 of the American Mathematical Society February 2006 Volume 53, Number 2 Math Circles and Olympiads MSRI Asks: Is the U.S. Coming of Age? page 200 A System of Axioms of Set Theory for the Rationalists page 206 Durham Meeting page 299 San Francisco Meeting page 302 ICM Madrid 2006 (see page 213) > To mak• an antmat•d tub• plot Animated Tube Plot 1 Type an expression in one or :;)~~~G~~~t;~~i~~~~~~~~~~~~~:rtwo ' 2 Wrth the insertion point in the 3 Open the Plot Properties dialog the same variables Tl'le next animation shows • knot Plot 30 Animated + Tube Scientific Word ... version 5.5 Scientific Word"' offers the same features as Scientific WorkPlace, without the computer algebra system. Editors INTERNATIONAL Morris Weisfeld Editor-in-Chief Enrico Arbarello MATHEMATICS Joseph Bernstein Enrico Bombieri Richard E. Borcherds Alexei Borodin RESEARCH PAPERS Jean Bourgain Marc Burger James W. Cogdell http://www.hindawi.com/journals/imrp/ Tobias Colding Corrado De Concini IMRP provides very fast publication of lengthy research articles of high current interest in Percy Deift all areas of mathematics. All articles are fully refereed and are judged by their contribution Robbert Dijkgraaf to the advancement of the state of the science of mathematics. Issues are published as S. K. Donaldson frequently as necessary. Each issue will contain only one article. IMRP is expected to publish 400± pages in 2006. Yakov Eliashberg Edward Frenkel Articles of at least 50 pages are welcome and all articles are refereed and judged for Emmanuel Hebey correctness, interest, originality, depth, and applicability. Submissions are made by e-mail to Dennis Hejhal [email protected].
    [Show full text]
  • Structure” of Physics: a Case Study∗ (Journal of Philosophy 106 (2009): 57–88)
    The “Structure” of Physics: A Case Study∗ (Journal of Philosophy 106 (2009): 57–88) Jill North We are used to talking about the “structure” posited by a given theory of physics. We say that relativity is a theory about spacetime structure. Special relativity posits one spacetime structure; different models of general relativity posit different spacetime structures. We also talk of the “existence” of these structures. Special relativity says that the world’s spacetime structure is Minkowskian: it posits that this spacetime structure exists. Understanding structure in this sense seems important for understand- ing what physics is telling us about the world. But it is not immediately obvious just what this structure is, or what we mean by the existence of one structure, rather than another. The idea of mathematical structure is relatively straightforward. There is geometric structure, topological structure, algebraic structure, and so forth. Mathematical structure tells us how abstract mathematical objects t together to form different types of mathematical spaces. Insofar as we understand mathematical objects, we can understand mathematical structure. Of course, what to say about the nature of mathematical objects is not easy. But there seems to be no further problem for understanding mathematical structure. ∗For comments and discussion, I am extremely grateful to David Albert, Frank Arntzenius, Gordon Belot, Josh Brown, Adam Elga, Branden Fitelson, Peter Forrest, Hans Halvorson, Oliver Davis Johns, James Ladyman, David Malament, Oliver Pooley, Brad Skow, TedSider, Rich Thomason, Jason Turner, Dmitri Tymoczko, the philosophy faculty at Yale, audience members at The University of Michigan in fall 2006, and in 2007 at the Paci c APA, the Joint Session of the Aristotelian Society and Mind Association, and the Bellingham Summer Philosophy Conference.
    [Show full text]
  • Volume 372 Number 6 Whole Number 1021 15 September 2019
    VOLUME 372 NUMBER 6 WHOLE NUMBER 1021 15 SEPTEMBER 2019 AMERICANMATHEMATICALSOCIETY EDITED BY Alejandro Adem, Managing Editor Vitaly Bergelson Richard Canary Lucia Caporaso Ted C. Chinburg Henri Darmon Patrick J. Fitzsimmons Noam Greenberg Jim Haglund Ailana M. Fraser Michael Hill Radha Kessar Joachim Krieger Alexander A. Kiselev Chiu-Chu Melissa Liu Svitlana Mayboroda Ian Melbourne Irena Peeva Robin Pemantle Lillian B. Pierce Stefaan Vaes Monica Visan Transactions of the American Mathematical Society This journal is devoted entirely to research in pure and applied mathematics. Submission information. See Information for Authors at the end of this issue. Publication on the AMS website. Articles are published on the AMS website in- dividually after proof is returned from authors and before appearing in an issue. Subscription information. Transactions of the American Mathematical Society is published monthly and is also accessible electronically from www.ams.org/journals/. Sub- scription prices for Volume 371 (2019) are as follows: for paper delivery, US$2853 list, US$2282.40 institutional member, US$2567.70 corporate member; for electronic delivery, US$2511 list, US$2008.80 institutional member, US$2259.90 corporate member. Upon request, subscribers to paper delivery of this journal are also entitled to receive electronic delivery. If ordering the paper version, add US$22 for delivery within the United States; US$170 for delivery outside the United States. Subscription renewals are subject to late fees. See www.ams.org/journal-faq for more journal subscription information. Back number information. For back issues see www.ams.org/backvols. Subscriptions and orders should be addressed to the American Mathematical Society, P.O.
    [Show full text]
  • Bfm:978-1-4612-2582-9/1.Pdf
    Progress in Mathematics Volume 131 Series Editors Hyman Bass Joseph Oesterle Alan Weinstein Functional Analysis on the Eve of the 21st Century Volume I In Honor of the Eightieth Birthday of I. M. Gelfand Simon Gindikin James Lepowsky Robert L. Wilson Editors Birkhauser Boston • Basel • Berlin Simon Gindikin James Lepowsky Department of Mathematics Department of Mathematics Rutgers University Rutgers University New Brunswick, NJ 08903 New Brunswick, NJ 08903 Robert L. Wilson Department of Mathematics Rutgers University New Brunswick, NJ 08903 Library of Congress Cataloging-in-Publication Data Functional analysis on the eve of the 21 st century in honor of the 80th birthday 0fI. M. Gelfand I [edited) by S. Gindikin, 1. Lepowsky, R. Wilson. p. cm. -- (Progress in mathematics ; vol. 131) Includes bibliographical references. ISBN-13:978-1-4612-7590-9 e-ISBN-13:978-1-4612-2582-9 DOl: 10.1007/978-1-4612-2582-9 1. Functional analysis. I. Gel'fand, I. M. (lzraU' Moiseevich) II. Gindikin, S. G. (Semen Grigor'evich) III. Lepowsky, J. (James) IV. Wilson, R. (Robert), 1946- . V. Series: Progress in mathematics (Boston, Mass.) ; vol. 131. QA321.F856 1995 95-20760 515'.7--dc20 CIP Printed on acid-free paper d»® Birkhiiuser ltGD © 1995 Birkhliuser Boston Softcover reprint of the hardcover 1st edition 1995 Copyright is not claimed for works of u.s. Government employees. All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without prior permission of the copyright owner.
    [Show full text]
  • Bart, Hempfling, Kaashoek. (Eds.) Israel Gohberg and Friends.. on The
    Israel Gohberg and Friends On the Occasion of his 80th Birthday Harm Bart Thomas Hempfling Marinus A. Kaashoek Editors Birkhäuser Basel · Boston · Berlin Editors: Harm Bart Marinus A. Kaashoek Econometrisch Instituut Department of Mathematics, FEW Erasmus Universiteit Rotterdam Vrije Universiteit Postbus 1738 De Boelelaan 1081A 3000 DR Rotterdam 1081 HV Amsterdam The Netherlands The Netherlands e-mail: [email protected] e-mail: [email protected] Thomas Hempfling Editorial Department Mathematics Birkhäuser Publishing Ltd. P.O. Box 133 4010 Basel Switzerland e-mail: thomas.hempfl[email protected] Library of Congress Control Number: 2008927170 Bibliographic information published by Die Deutsche Bibliothek Die Deutsche Bibliothek lists this publication in the Deutsche Nationalbibliografie; detailed bibliographic data is available in the Internet at <http://dnb.ddb.de>. ISBN 978-3-7643-8733-4 Birkhäuser Verlag, Basel – Boston – Berlin This work is subject to copyright. All rights are reserved, whether the whole or part of the material is concerned, specifically the rights of translation, reprinting, re-use of illustrations, recitation, broadcasting, reproduction on microfilms or in other ways, and storage in data banks. For any kind of use permission of the copyright owner must be obtained. © 2008 Birkhäuser Verlag AG Basel · Boston · Berlin P.O. Box 133, CH-4010 Basel, Switzerland Part of Springer Science+Business Media Printed on acid-free paper produced of chlorine-free pulp. TCF ∞ Printed in Germany ISBN 978-3-7643-8733-4 e-ISBN 978-3-7643-8734-1 9 8 7 6 5 4 3 2 1 www.birkhauser.ch Contents Preface.......................................................................ix CongratulationsfromthePublisher...........................................xii PartI.MathematicalandPhilosophical-MathematicalTales...................1 I.
    [Show full text]
  • Pure Mathematics Professors Teaching and Leading Research CO-OP OR REGULAR 28
    PURE MATHEMATICS Pure Mathematics professors teaching and leading research CO-OP OR REGULAR 28 Mathematician ranked among top 10 TOP 10 jobs from 2011-2017 – Comcast.com of grads are employed Search for a deeper 96.6% within 2 years understanding of mathematics Pure mathematics is at the foundation of all mathematical reasoning. If first-year calculus ALEX teaches you how to drive the car, Pure Mathematics teaches you how to build one. 3B, PURE MATHEMATICS AND Mathematicians know that there could be no general relativity without differential COMBINATORICS AND geometry, and no computer security without advanced number theory. OPTIMIZATION Pure Mathematics at Waterloo is a small, cohesive, and challenging program that will open countless doors for you. Our graduates have used the program as a springboard into careers WHAT DO YOU LOVE ABOUT in information technology, finance, business, science, education, and insurance, often by way PURE MATHEMATICS? The satisfaction from understanding of some of the most prestigious graduate programs in the world. an idea at a deeper level and tying together unrelated branches of ALEX’S FAVOURITE COURSES mathematics or physics for the › PMATH 320 Euclidean Geometry: This course is everything you love about Geometry: first time is the most rewarding Euclid’s axioms, isometries of the Euclidean plane and of Euclidean space, polygons, part of learning and understanding polyhedral, polytopes, and the kissing problem. mathematics. What I really enjoy is › PMATH 351 Real Analysis: It’s a very intuitive and natural approach to real analysis, and the developing a deep understanding of complexity of the course builds very naturally to the end of the semester.
    [Show full text]
  • Mathematician Awarded Nobel Prize Growing Optimism That Fermat's
    THE NEWSLETTER OF THE MATHEMATICAL ASSOCIATION OF AMERICA Mathematician Awarded Nobel Prize Volume 14, Number 6 Keith Devlin The awarding of the Nobel Prize in econom­ It was the application ics to the American John Nash on October of Nash's work in eco­ II th meant that for the firsttime in the 93-year nomic theory that led to history of the Nobel Prizes, the prize was his recent Nobel Prize, In this Issue awarded for work in pure mathematics. which he shares with fellow American John When the Swedish chemist, engineer, and phi­ Harsanyi and German 3 MAA Secretary's lanthropistAlfred Bernhard Nobel established Reinhard Selten. Report the awards in 1901, he stipulated chemistry, Nash's contribution to physics, physiology and medicine, and litera­ the combined work ture, but did not create a prize for mathematics. 4 Joint Mathematics which won the award It has been rumored that a particularly bad was in game theory. Meetings Update experience in mathematics at high school led to this exclusion of the "queen of sciences", or Nash's key idea-known nowadays as Nash 6 Search Committee it may simply be that Nobel felt that math­ equilibrium-was developed in his Ph.D. the­ Diary ematics was not, in itself, of sufficient sis submitted to the Princeton University relevance to human development to warrant Mathematics Department in 1950, when Nash its own award. Whateverthe reason, the math­ was just 22 years old. The thesis had taken him 10 Networks in ematicians have had to make do with their a mere two years to complete.
    [Show full text]
  • All That Math Portraits of Mathematicians As Young Researchers
    Downloaded from orbit.dtu.dk on: Oct 06, 2021 All that Math Portraits of mathematicians as young researchers Hansen, Vagn Lundsgaard Published in: EMS Newsletter Publication date: 2012 Document Version Publisher's PDF, also known as Version of record Link back to DTU Orbit Citation (APA): Hansen, V. L. (2012). All that Math: Portraits of mathematicians as young researchers. EMS Newsletter, (85), 61-62. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. Users may download and print one copy of any publication from the public portal for the purpose of private study or research. You may not further distribute the material or use it for any profit-making activity or commercial gain You may freely distribute the URL identifying the publication in the public portal If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. NEWSLETTER OF THE EUROPEAN MATHEMATICAL SOCIETY Editorial Obituary Feature Interview 6ecm Marco Brunella Alan Turing’s Centenary Endre Szemerédi p. 4 p. 29 p. 32 p. 39 September 2012 Issue 85 ISSN 1027-488X S E European M M Mathematical E S Society Applied Mathematics Journals from Cambridge journals.cambridge.org/pem journals.cambridge.org/ejm journals.cambridge.org/psp journals.cambridge.org/flm journals.cambridge.org/anz journals.cambridge.org/pes journals.cambridge.org/prm journals.cambridge.org/anu journals.cambridge.org/mtk Receive a free trial to the latest issue of each of our mathematics journals at journals.cambridge.org/maths Cambridge Press Applied Maths Advert_AW.indd 1 30/07/2012 12:11 Contents Editorial Team Editors-in-Chief Jorge Buescu (2009–2012) European (Book Reviews) Vicente Muñoz (2005–2012) Dep.
    [Show full text]
  • Pure Mathematics
    Why Study Mathematics? Mathematics reveals hidden patterns that help us understand the world around us. Now much more than arithmetic and geometry, mathematics today is a diverse discipline that deals with data, measurements, and observations from science; with inference, deduction, and proof; and with mathematical models of natural phenomena, of human behavior, and social systems. The process of "doing" mathematics is far more than just calculation or deduction; it involves observation of patterns, testing of conjectures, and estimation of results. As a practical matter, mathematics is a science of pattern and order. Its domain is not molecules or cells, but numbers, chance, form, algorithms, and change. As a science of abstract objects, mathematics relies on logic rather than on observation as its standard of truth, yet employs observation, simulation, and even experimentation as means of discovering truth. The special role of mathematics in education is a consequence of its universal applicability. The results of mathematics--theorems and theories--are both significant and useful; the best results are also elegant and deep. Through its theorems, mathematics offers science both a foundation of truth and a standard of certainty. In addition to theorems and theories, mathematics offers distinctive modes of thought which are both versatile and powerful, including modeling, abstraction, optimization, logical analysis, inference from data, and use of symbols. Mathematics, as a major intellectual tradition, is a subject appreciated as much for its beauty as for its power. The enduring qualities of such abstract concepts as symmetry, proof, and change have been developed through 3,000 years of intellectual effort. Like language, religion, and music, mathematics is a universal part of human culture.
    [Show full text]
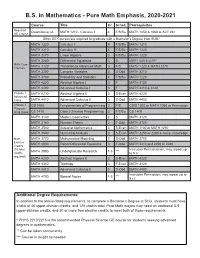
  • B.S. in Mathematics - Pure Math Emphasis, 2020-2021
    B.S. in Mathematics - Pure Math Emphasis, 2020-2021 Course Title Cr. Sched. Prerequisites Required Quantitative Lit. MATH 1210 - Calculus I 4 F/S/Su MATH 1050 & 1060 or ACT 26+ GE Course Other GE Courses are required to graduate with a Bachelor’s Degree from SUU.* MATH 1220 Calculus II 4 F/S/Su MATH 1210 MATH 2210 Calculus III 4 F/S/Su MATH 1220 MATH 2270 Linear Algebra 3 F/S/Su MATH 1220 MATH 2280 Differential Equations 3 S MATH 1220 & 2270** Math Core MATH 3120 Transition to Advanced Math 3 F/S MATH 1220 & MATH 2270 Courses MATH 3250 Complex Variables 3 S-Odd MATH 2210 MATH 3700 Probability and Statistics 4 F/S/Su MATH 1220 MATH 4220 Abstract Algebra I 3 F MATH 3120 MATH 4400 Advanced Calculus I 3 F MATH 2210 & 3120 Choose 1 MATH 4230 Abstract Algebra II 3 S-Even MATH 4220 Advanced Class MATH 4410 Advanced Calculus II 3 S-Odd MATH 4400 Choose 1 CS 1400 Fundamentals of Programming 3 F/S CSIS 1030 or MATH 1050 or Permission Program- ming Class CS 1410 Object Oriented Programming 3 F/S/Su CS 1400 MATH 3130 Modern Geometries 3 S MATH 3120 MATH 3160 Number Theory 3 F-Odd MATH 3120 MATH 3500 Actuarial Mathematics 3 S-Even MATH 1100 or MATH 1210 MATH 3600 Numerical Analysis 3 S-Even MATH 2250 or 2280 & comp. knowledge Math MATH 3770 Mathematical Modeling 3 S-Odd MATH 3700 Elective MATH 3800 Partial Differential Equations 3 F-Odd MATH 2210 and 2250 or 2280 Credits (15 total Instructor Permissission; may repeat up MATH 3990 Undergraduate Research 1-3 *** credits to 5 cr.
    [Show full text]
  • Axiomatic Foundations of Mathematics Ryan Melton Dr
    Axiomatic Foundations of Mathematics Ryan Melton Dr. Clint Richardson, Faculty Advisor Stephen F. Austin State University As Bertrand Russell once said, Gödel's Method Pure mathematics is the subject in which we Consider the expression First, Gödel assigned a unique natural number to do not know what we are talking about, or each of the logical symbols and numbers. 2 + 3 = 5 whether what we are saying is true. Russell’s statement begs from us one major This expression is mathematical; it belongs to the field For example: if the symbol '0' corresponds to we call arithmetic and is composed of basic arithmetic question: the natural number 1, '+' to 2, and '=' to 3, then symbols. '0 = 0' '0 + 0 = 0' What is Mathematics founded on? On the other hand, the sentence and '2 + 3 = 5' is an arithmetical formula. 1 3 1 1 2 1 3 1 so each expression corresponds to a sequence. Axioms and Axiom Systems is metamathematical; it is constructed outside of mathematics and labels the expression above as a Then, for this new sequence x1x2x3…xn of formula in arithmetic. An axiom is a belief taken without proof, and positive integers, we associate a Gödel number thus an axiom system is a set of beliefs as follows: x1 x2 x3 xn taken without proof. enc( x1x2x3...xn ) = 2 3 5 ... pn Since Principia Mathematica was such a bold where the encoding is the product of n factors, Consistent? Complete? leap in the right direction--although proving each of which is found by raising the j-th prime nothing about consistency--several attempts at to the xj power.
    [Show full text]