DOCSLIB.ORG

SPECIAL SECTION Civilisation Dated 1900-1600 BC Has a Circle's Circumference Instead of the Statement That Implicates a Value of Area

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
SPECIAL SECTION Civilisation Dated 1900-1600 BC Has a Circle's Circumference Instead of the Statement That Implicates a Value of Area SPECIAL SECTION civilisation dated 1900-1600 BC has a circle's circumference instead of the statement that implicates a value of area. This algorithm was devised around 3.1250 to pi. In the Egyptian civilisation 250 BC and dominated for over 1000 (around 1650 BC), the area of a circle years, as a result of which pi is was calculated by using an approximate sometimes referred as ‘Archimedes value of 3.1605 as pi. In Egypt, the constant’. He developed a polygon Rhind Papyrus, dates around 1650 BC, approach to approximate the value of pi but copied from a document dated 1850 and found the upper and lower bounds BC mentions the formula for the area of of pi by inscribing and circumscribing a a circle that treats pi as 3.1605. In India circle in a hexagon, and successively around 600 BC, some Sanskrit texts doubling the number of sides. He did treat pi as equal to 3.088. this until he obtained a 96-sided polygon. By calculations involving the When Greeks took up the problem, they perimeters of these polygons, he took two revolutionary steps to find pi. obtained the bounds of pi and proved Antiphon and Bryson of Heraclea came that 3.1408 < pi< 3.1429. Around 150 up with the idea of drawing a polygon AD, Greek-Roman scientist Ptolemy inside a circle, finding its area, and gave a value of 3.1416 in his Almagest, doubling the sides repeatedly. Later, which he may have obtained from Bryson also calculated the area of Archimedes or from Apollonius of polygons circumscribing the circle. Perga. Using this algorithm, Perhaps this was first time that a mathematicians reached 39 digits of pi mathematical result for pi was in 1630, a record unbroken until 1699 determined by using upper and lower when the infinite series approach was bounds. The first man who really made devised. a serious attempt to calculate the value of pi was a Greek scientist Archimedes In China, in around 265 AD, Liu Hui, a of Syracuse. Archimedes carried Wei kingdom mathematician created a forward the work of Antiphon and polygon-based iterative algorithm and Bryson. However, his approach was implemented it with a 3072-sided slightly different from Antiphon and polygon to obtain a value of 3.1416. He Bryson. Archimedes focused on the later invented a faster method and polygon's perimeters as opposed to their obtained a value of 3.14 with a 96-sided areas, so that he approximated the polygon, using the fact that differences New Horizons, Vol. 2 December 2016 SPECIAL SECTION in the area of successive polygons form European mathematicians used infinite a geometric series with a factor of 4. series to compute pi with greater Another mathematician ZuChongzhi accuracy. The first infinite sequence was applied Liu’s algorithm to a 12288- discovered by French mathematician sided polygon and calculated the correct Francois Viete. He used Archimedean value of its first seven decimal digits. method. Francois started with two This value remained the best hexagons and then doubling the number approximation for the next 800 years. In of sides sixteen times, and finally the 5th century, TsuCh'ung-chih and his finishing with 393,216 sides. His final son TsuKeng-chih calculated the value result was that 3.1415926535 < pi < of pi ranging between 3.1415926 and 3.1415926537. Adrianus Romanus, in 3.1415927 by inscribing polygon with 1593, computed pi with the accuracy to as many as 24,576 sides. In the same 15 digits after the decimal by using a period, the Hindu mathematician circumscribed polygon with 230 sides. Aryabhata calculated better After few years, Ludolph Van Ceulen, a approximation 62,832/20,000 = 3.1416 German presented 20 digits, using the (as against Archimedes’ 22/7 which was Archimedean method with polygons frequently used), but this value did not with over 500 million sides. Van Ceulen get any noticeable attention. Another spent a great part of his life hunting for Indian mathematician, Brahmagupta, pi, and he had computed pi up to 35 took a novel approach by calculating the digits after decimal. To recognize his perimeters of inscribed polygons with work, the digits were written into his 12, 24, 48, and 96. He observed that as tombstone in St. Peter's Churchyard in the polygons approached the circle, the Leyden. Here, it is important to mention perimeter, and therefore pi, would that up to this time, there was no symbol approach the square root of 10 [= to denote the ratio of a circle's 3.162...]. In 9th century, mathematics circumference to its diameter. This and science prospered in the Arab changed in 1647 when William cultures. It is stated that, in some texts, Oughtred published Clavis that the Arabian mathematician, Mathematicae and used (/(to denote the Mohammed bin Musa al'Khwarizmi, ratio. It was not accepted immediately attempted to calculate pi approximately but in 1737 when Leonhard Euler began 21/7. During the 16th and 17th centuries, using the symbol for pi; then it was New Horizons, Vol. 2 December 2016 SPECIAL SECTION quickly accepted. In 1650, John Wallis William Shanks used the formula to used a very complicated method to find calculate 707 places of pi. another formula for pi. He approximated Many years later, it was discovered that the area of a quarter circle using somewhere along the line, Shanks had infinitely small rectangles, and arrived left two terms as a result only the first at the formula for 4/pi which is 527 digits were correct. Machin-like simplified to pi/2. In 1672, James variants were subsequently created by Gregory wrote about a formula that can others who created records for 250 years be used to calculate the angle given the and more. Daniel Ferguson achieved a tangent for angles up to 45pi. After ten 620-digit approximation in 1946, which years, Gottfried Leibnitz pointed out was the best possible approximation that since tan pi/4 = 1, the formula could without the use of a calculating device. be used to find pi. Thus, one of the By 1750, the number pi had been most famous formulas for calculating pi expressed by infinite series, its value was realized: (/4 = 1 - 1/3 + 1/5 - 1/7 + had been computed [to over 100 digits] 1/9.... This elegant formula is one of the and it had been given its present symbol. simplest ever discovered to calculate pi, All these efforts, however, had not but it was also useless; 300 terms of the contributed to the solution of the ancient series are required to get only 2 decimal problem of the quadrature of the circle. places, and 10,000 terms are required The first step was taken by the Swiss for 4 decimal places. To compute 100 mathematician Johann Heinrich digits, one has to calculate more terms Lambert when he proved the than there are particles in the universe. irrationality of pi first in 1761 and then Better approximations of PI in more detail in 1767. His argument In 1706, John Machin, a professor of was, in its simplest form, that if x is a astronomy in London, took an initiative rational number, then tan x cannot be to calculate pi with his new formula, and rational; since tan pi/4 = 1, pi/4 cannot computed 100 places by hand. Over the be rational, and therefore pi is irrational. next 150 year, several men used the Some people felt that his proof was not same formula to find more and more rigorous enough, but in 1794, Adrien digits. In 1873, an Englishman named Marie Legendre gave another proof that satisfied everyone. Furthermore, New Horizons, Vol. 2 December 2016 SPECIAL SECTION Legendre also gave the first proof that in 1949, another breakthrough emerged, square root of 2 is irrational. In 1882, but it was not mathematical in nature; it Ferdinand von Lindemann proved the was the speed with which the transcendence of pi. Since this means calculations could be done. The ENIAC that pi is not a solution of any algebraic (Electronic Numerical Integrator and equation, it lay to rest the uncertainty Computer) was finally completed and about squaring the circle. Finally, after functional, and a group of literally thousands and thousands of mathematicians headed by John von lifetimes of mental toil and strain, Neumann fed in punch cards and let the mathematicians finally had an absolute gigantic machine calculate 2037 digits answer that the circle could not be in just seventy hours; whereas it took squared. Nonetheless, there are still Shanks several years to come up with some amateur mathematicians today his 707 digits, and Ferguson needed who do not understand the significance about one year to get 808 digits. With of this result, and look for techniques to the invention of the electronic computer, square the circle. John Wrench and Daniel Shanks found 100,000 digits in 1961, and the one- PI in computer Era million-mark was surpassed in 1973. In The computer era further saw 1976, Eugene Salamin developed an developments in the calculation of more algorithm that doubles the number of number of digits of pi. The discovery of correct digits with each iteration. After iterative algorithms independent of the development of this algorithm, the infinite series, and fast multiplication number of digits of pi increased algorithms led to further increase in enormously. After 1980, iterative these developments. In 1945, D. F. algorithms that were faster than infinite Ferguson discovered the error in series algorithms were used, since William Shanks' calculation from the iterative algorithms multiply the number 528th digit onward.
Load more

Recommended publications
  • History of the Numerical Methods of Pi
    History of the Numerical Methods of Pi By Andy Yopp MAT3010 Spring 2003 Appalachian State University This project is composed of a worksheet, a time line, and a reference sheet. This material is intended for an audience consisting of undergraduate college students with a background and interest in the subject of numerical methods. This material is also largely recreational. Although there probably aren't any practical applications for computing pi in an undergraduate curriculum, that is precisely why this material aims to interest the student to pursue their own studies of mathematics and computing. The time line is a compilation of several other time lines of pi. It is explained at the bottom of the time line and further on the worksheet reference page. The worksheet is a take-home assignment. It requires that the student know how to construct a hexagon within and without a circle, use iterative algorithms, and code in C. Therefore, they will need a variety of materials and a significant amount of time. The most interesting part of the project was just how well the numerical methods of pi have evolved. Currently, there are iterative algorithms available that are more precise than a graphing calculator with only a single iteration of the algorithm. This is a far cry from the rough estimate of 3 used by the early Babylonians. It is also a different entity altogether than what the circle-squarers have devised. The history of pi and its numerical methods go hand-in-hand through shameful trickery and glorious achievements. It is through the evolution of these methods which I will try to inspire students to begin their own research.
    [Show full text]
  • Perimeter, Area, and Volume
    Perimeter, Area, and Volume Perimeter is a measurement of length. It is the distance around something. We use perimeter when building a fence around a yard or any place that needs to be enclosed. In that case, we would measure the distance in feet, yards, or meters. In math, we usually measure the perimeter of polygons. To find the perimeter of any polygon, we add the lengths of the sides. 2 m 2 m P = 2 m + 2 m + 2 m = 6 m 2 m 3 ft. 1 ft. 1 ft. P = 1 ft. + 1 ft. + 3 ft. + 3 ft. = 8 ft. 3ft When we measure perimeter, we always use units of length. For example, in the triangle above, the unit of length is meters. For the rectangle above, the unit of length is feet. PRACTICE! 1. What is the perimeter of this figure? 5 cm 3.5 cm 3.5 cm 2 cm 2. What is the perimeter of this figure? 2 cm Area Perimeter, Area, and Volume Remember that area is the number of square units that are needed to cover a surface. Think of a backyard enclosed with a fence. To build the fence, we need to know the perimeter. If we want to grow grass in the backyard, we need to know the area so that we can buy enough grass seed to cover the surface of yard. The yard is measured in square feet. All area is measured in square units. The figure below represents the backyard. 25 ft. The area of a square Finding the area of a square: is found by multiplying side x side.
    [Show full text]
  • Rectangles with the Same Numerical Area and Perimeter
    Rectangles with the Same Numerical Area and Perimeter About Illustrations: Illustrations of the Standards for Mathematical Practice (SMP) consist of several pieces, including a mathematics task, student dialogue, mathematical overview, teacher reflection questions, and student materials. While the primary use of Illustrations is for teacher learning about the SMP, some components may be used in the classroom with students. These include the mathematics task, student dialogue, and student materials. For additional Illustrations or to learn about a professional development curriculum centered around the use of Illustrations, please visit mathpractices.edc.org. About the Rectangles with the Same Numerical Area and Perimeter Illustration: This Illustration’s student dialogue shows the conversation among three students who are trying to find all rectangles that have the same numerical area and perimeter. After trying different rectangles of specific dimensions, students finally develop an equation that describes the relationship between the width and length of a rectangle with equal area and perimeter. Highlighted Standard(s) for Mathematical Practice (MP) MP 1: Make sense of problems and persevere in solving them. MP 2: Reason abstractly and quantitatively. MP 7: Look for and make use of structure. MP 8: Look for and express regularity in repeated reasoning. Target Grade Level: Grades 8–9 Target Content Domain: Creating Equations (Algebra Conceptual Category) Highlighted Standard(s) for Mathematical Content A.CED.A.2 Create equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales. A.CED.A.4 Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations.
    [Show full text]
  • Area and Perimeter What Is the Formula for Perimeter and How Is It Applied in Construction?
    Name: Basic Carpentry Coop Tech Morning/Afternoon Canarsie HS Campus Mr. Pross Finding Area and Perimeter What is the formula for perimeter and how is it applied in construction? 1. Perimeter: The perimeter of a rectangle is the distance around it. Therefore, the perimeter is the sum of all four sides. Perimeter is important when calculating estimates for materials needed for completing a job. Example: Before ordering baseboard trim, the must wrap around the entire room, the perimeter of a 12’ 12 ft x 18 ft room must be found. What is the perimeter of the room? 18’ What is the formula for perimeter? Write it below. _______________________ 1. This is the formula you will need to follow in order to calculate area. = 2 (12 ft + 18 ft) 2. Add the length and width in parentheses. The length plus the width represent halfway around the room. = 2 (30 ft) 3. Multiply the sum of the length and width by 2 to find the entire distance around. = 60 ft. Practice A client asked that you to install a new window. The framing though is too small and you need to demolish it and rebuild it. First you need to find the perimeter of the window. If this window measures 32 inches by 42 inches, what is the perimeter? Name: Basic Carpentry Coop Tech Morning/Afternoon Canarsie HS Campus Mr. Pross 2. Area: The area of a square is the surface included within a set of lines. In carpentry, this means the total space of a room or even a building. Area, like permiter, is an important mathematical formula for estimating material and cost in construction.
    [Show full text]
  • Perimeter , Area and Volume with Changed Dimensions
    Perimeter , Area and Volume with changed dimensions Given a rectangle with dimensions of 6 by 4. Perimeter: __________ Area: ______________ Double the dimensions of the rectangle (multiply each side by 2) New Perimeter: ___________ New Area: _______________ Compare the effects on the perimeter and area when dimensions of a shape are changed (dilated) proportionally. Complete the chart below: Smaller Larger Ratio of larger Rectangle Rectangle dimension to smaller dimension Length Width Perimeter Area Conclusion: Perimeter , Area and Volume with changed dimensions If the dimensions of the rectangle are doubled (scale factor of 2): the perimeter is___________ If the dimensions of the rectangles are doubled (scale factor of 2): the area is ____________ Extension: If the dimensions of the rectangle are tripled (scale factor of 3): the perimeter is ______________ If the dimensions of the rectangle are triples (scale factor of 3): the area is ___________________ What do you think will happen to volume when dimensions are changed proportionally? Given a rectangular prism with dimensions of 6 by 4 by 2: Volume: _____________ Double the dimensions of the prism: New Volume: __________ Perimeter , Area and Volume with changed dimensions Smaller Rectangle Larger Rectangle Ratio of larger dimension to smaller dimension Length Width Height Volume Since each dimension was dilated (multiplied) by 2, then the volume was multiplied by 8: or 23 (scale factor cubed) Why do you think the volume is “cubed”? Perimeter , Area and Volume with changed dimensions Effects on perimeter, area and volume when dimensions of a shape are changed proportionally: Original Scale factor Perimeter Area Volume times 2 times 2=___ times 22=___ times 23=___ times 3 times 4 1 times 2 2 times 3 3 times 4 Examples: 1.
    [Show full text]
  • Π and Its Computation Through the Ages
    π and its computation through the ages Xavier Gourdon & Pascal Sebah http://numbers.computation.free.fr/Constants/constants.html August 13, 2010 The value of π has engaged the attention of many mathematicians and calculators from the time of Archimedes to the present day, and has been computed from so many different formulae, that a com- plete account of its calculation would almost amount to a history of mathematics. - James Glaisher (1848-1928) The history of pi is a quaint little mirror of the history of man. - Petr Beckmann 1 Computing the constant π Understanding the nature of the constant π, as well as trying to estimate its value to more and more decimal places has engaged a phenomenal energy from mathematicians from all periods of history and from most civilizations. In this small overview, we have tried to collect as many as possible major calculations of the most famous mathematical constant, including the methods used and references whenever there are available. 1.1 Milestones of π's computation • Ancient civilizations like Egyptians [15], Babylonians, China ([29], [52]), India [36],... were interested in evaluating, for example, area or perimeter of circular fields. Of course in this early history, π was not yet a constant and was only implicit in all available documents. Perhaps the most famous is the Rhind Papyrus which states the rule used to compute the area of a circle: take away 1/9 of the diameter and take the square of the remainder therefore implicitly π = (16=9)2: • Archimedes of Syracuse (287-212 B.C.). He developed a method based on inscribed and circumscribed polygons which will be of practical use until the mid seventeenth.
    [Show full text]
  • Section 3.3: Circles 3
    Section 3.3: Circles 3 Contents at a Glance Pretest 167 Section Challenge 172 Lesson A: What’s in a Circle? 173 Lesson B: What is Pi? 187 Lesson C: Circumference of a Circle 197 Lesson D: Area of a Circle 211 Section Summary 225 Learning Outcomes By the end of this section you will be better able to: • identify the components and characteristics of circles. • describe the relationships between the parts of a circle. • construct circles using geometric tools. • apply a formula to fi nd the circumference and area of a circle. • solve problems that involve fi nding the circumference or area of a circle. • solve problems involving the area of triangles, parallelograms, and/or circles. © Open School BC MATH 7 eText 165 Module 3, Section 3 166 MATH 7 eText © Open School BC Module 3, Section 3 Pretest 3.3 Pretest 3.3 Complete this pretest if you think that you already have a strong grasp of the topics and concepts covered in this section. Mark your answers using the key found at the end of the module. If you get all the answers correct (100%), you may decide that you can omit the lesson activities. 1. Fill in the blanks: a. The ____________________ is a point inside a circle from which all points on the circumference are the same distance. b. The ________________ is the longest chord that can be drawn inside a circle. c. The diameter is ____________________ times as large as the radius. d. The ____________________ is the distance around the circle. e. A diameter is a line segment drawn from one point on a circle to another point that passes through the ____________________.
    [Show full text]
  • 1.7 Find Perimeter, Circumference, and Area
    &IND 0ERIMETER #IRCUMFERENCE AND !REA 'OAL + &IND DIMENSIONS OF POLYGONS &/2-5,!3 &/2 0%2)-%4%2 0 !2%! ! !.$ 9OUR .OTES #)2#5-&%2%.#% # 3QUARE 2ECTANGLE SIDE LENGTH S LENGTH * AND WIDTH W 0 Ê{ÃÊ 0 ÊÓ*ÊzÓÜÊ ! Ê ÃÓÊ ! Ê *ÜÊ 4RIANGLE #IRCLE SIDE LENGTHS A B RADIUS R AND C BASE B # ÊÓ:ÀÊ AND HEIGHT H ! Ê :À ÓÊ 0 Ê >ÊzLÊzVÊ 0I : IS THE RATIO OF A £ ! ÊÊÊ]ÊÊÊL z Ê CIRCLEgS CIRCUMFERENCE TO Ó ITS DIAMETER %XAMPLE &IND THE PERIMETER AND AREA OF A RECTANGLE 4ENNIS 4HE IN BOUNDS PORTION OF A SINGLES TENNIS COURT IS SHOWN &IND ITS PERIMETER AND AREA 0ERIMETER !REA 0 * W ! *W ÊÇnÊ ÊÓÇÊ ÊÇnÊÊÓÇÊ ÊÓ£äÊ ÊÓ£äÈÊ 4HE PERIMETER IS ÊÓ£äÊ FT AND THE AREA IS ÊÓ£äÈÊ FT #HECKPOINT #OMPLETE THE FOLLOWING EXERCISE )N %XAMPLE THE WIDTH OF THE IN BOUNDS RECTANGLE INCREASES TO FEET FOR DOUBLES PLAY &IND THE PERIMETER AND AREA OF THE IN BOUNDS RECTANGLE ÊÊ«iÀiÌiÀ\ÊÓÓnÊvÌ]Ê>Ài>\ÊÓnänÊvÌÓ ,ESSON s 'EOMETRY .OTETAKING 'UIDE #OPYRIGHT Ú -C$OUGAL ,ITTELL(OUGHTON -IFFLIN #OMPANY 9OUR .OTES %XAMPLE &IND THE CIRCUMFERENCE AND AREA OF A CIRCLE !RCHERY 4HE SMALLEST CIRCLE ON AN /LYMPIC TARGET IS 4HE APPROXIMATIONS CENTIMETERS IN DIAMETER &IND THE APPROXIMATE AND ]zARE CIRCUMFERENCE AND AREA OF THE SMALLEST CIRCLE COMMONLY USED AS APPROXIMATIONS 3OLUTION FOR THE IRRATIONAL &IRST FIND THE RADIUS 4HE DIAMETER IS CENTIMETERS NUMBER : 5NLESS SO THE RADIUS IS ]zÊ£ÓÊ ÊÈÊ CENTIMETERS TOLD OTHERWISE USE FOR : 4HEN FIND THE CIRCUMFERENCE AND AREA 5SE FOR : 0 :R yzÊΰ£{Ê ÊÈÊ ÊÎÇ°ÈnÊVÊ ! :R yzÊΰ£{ÊÊÈÊ Ê££Î°ä{ÊVÓÊ #HECKPOINT &IND THE APPROXIMATE
    [Show full text]
  • Daf Ditty Eruvin 14 Pi, Revised X2
    Daf Ditty Eruvin 14: Pi, the Ratio of God “Human beings, vegetables, or cosmic dust, we all dance to a mysterious tune intoned in the distance by an invisible player.” – Albert Einstein “The world isn't just the way it is. It is how we understand it, no? And in understanding something, we bring something to it, no? Doesn't that make life a story?” "Love is hard to believe, ask any lover. Life is hard to believe, ask any scientist. God is hard to believe, ask any believer... be excessively reasonable and you risk throwing out the universe with the bathwater." Yann Martel, Life of Pi 1 The mishna continues: If the cross beam is round, one considers it as though it were square. The Gemara asks: Why do I need this clause as well? Similar cases were already taught in the mishna. The Gemara answers: It was necessary to teach the last clause of this section, i.e., the principle that any circle with a circumference of three handbreadths is a handbreadth in diameter. 2 The Gemara asks: From where are these matters, this ratio between circumference and diameter, derived? Rabbi Yoḥanan said that the verse said with regard to King Solomon: And he made the molten sea of ten cubits from 23 גכ את ַַַויּﬠֶשׂ - ָוּ,מצםיַּה ָ:ק ֶֶﬠשׂ ר אָ בּ מַּ הָ הָ מַּ אָ בּ ר brim to brim, round in compass, and the height thereof תוֹפדשּׂﬠ ְִָמַ - ﬠוֹתְשׂפ סלָגָ ִ,יבָבֹ בּשְׁמחו ַהמֵָּאָ ָ ַהמֵָּאָ בּשְׁמחו ִ,יבָבֹ סלָגָ ﬠוֹתְשׂפ was five cubits; and a line of thirty cubits did compass וֹקמ ,וֹתָ וקוה ו( קְ ָ )ו םיִשׁhְ שׁ אָ בּ מַּ ,הָ סָ י בֹ וֹתֹ א וֹתֹ א בֹ סָ י ,הָ מַּ אָ בּ םיִשׁhְ שׁ )ו ָ קְ ו( וקוה ,וֹתָ וֹקמ .it round about ִי.בָסב I Kings 7:23 “And he made a molten sea, ten cubits from the one brim to the other: It was round all about, and its height was five cubits; and a line of thirty cubits did circle it roundabout” The Gemara asks: But isn’t there its brim that must be taken into account? The diameter of the sea was measured from the inside, and if its circumference was measured from the outside, this ratio is no longer accurate.
    [Show full text]
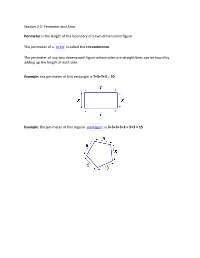
  • Section 2.2: Perimeter and Area
    Section 2.2: Perimeter and Area Perimeter is the length of the boundary of a two dimensional figure. The perimeter of a circle is called the circumference. The perimeter of any two dimensional figure whose sides are straight lines can be found by adding up the length of each side. Example: the perimeter of this rectangle is 7+3+7+3 = 20 Example: the perimeter of this regular pentagon is 3+3+3+3+3 = 5×3 = 15 There are formulas that can help us find the perimeter of a few standard shapes. However, if a two dimensional shape has a border that consists of only straight lines simply adding up the lengths of each side will be sufficient to find the perimeter. I will need to use a formula to find the perimeter (circumference) of a circle as its border is not made of straight lines. Perimeter Formulas Triangle Perimeter = a + b + c Square Perimeter = 4 × a a = length of side Rectangle Perimeter = 2 × (w + h) Or 2(length + width) w = width h = height Quadrilateral Perimeter = a + b + c + d Circle Circumference = 2πr r = radius Example: Use the appropriate formula to find the perimeter of the rectangle below. I will use the formula: Perimeter = 2(length + width) It is customary to call the longer side of a rectangle the length. I will replace the length in the formula with 7 yards, and the width with 4 yards. Perimeter = 2(7 yards + 4 yards) = 2(11 yards) Answer: Perimeter = 22 yards (The units in a perimeter problem are linear and do not have squares.) Example: Find the circumference of the following circle.
    [Show full text]
  • Perimeter, Diameter and Area of Convex Sets in the Hyperbolic Plane
    PERIMETER, DIAMETER AND AREA OF CONVEX SETS IN THE HYPERBOLIC PLANE. EDUARDO GALLEGO AND GIL SOLANES Abstract. In this paper we study the relation between the asymptotic values of the ratios area/length (F/L) and diameter/length (D/L) of a sequence of convex sets expanding over the whole hyperbolic plane. It is known (cf. [3] and [2]) that F/L goes to a value between 0 and 1 depending on the shape of the contour. Here, rst of all it is seen that D/L has limit value between 0 and 1/2 in strong contrast with the euclidean situation in which the lower bound is 1/ (D/L = 1/ if and only if the convex set has constant width). Moreover, it is shown that, as the limit of D/L approaches to 1/2, the possible limit values of F/L reduce. Examples of all possible limits F/L and D/L are given. 1. Introduction In hyperbolic geometry, given a point p exterior to a line l there are innitely many non secant lines. These lines lie between the two so called parallel lines to l. When the distance from p to l grows to innity, the angle between the parallel lines goes to 0. This fact leads to the ambiguous idea that, in some sense, given a line l, the probability that a random line meets l is zero. In order to formalize this idea let us restrict our attention to the interiors of a sequence (Kn) of convex sets in the hyperbolic plane expanding to ll it.
    [Show full text]
  • AREA and VOLUME WHERE DO the FORMULAS COME FROM? Roger Yarnell John Carroll University, [email protected]
    John Carroll University Carroll Collected Masters Essays Theses, Essays, and Senior Honors Projects Spring 2016 AREA AND VOLUME WHERE DO THE FORMULAS COME FROM? Roger Yarnell John Carroll University, [email protected] Follow this and additional works at: http://collected.jcu.edu/mastersessays Part of the Geometry and Topology Commons Recommended Citation Yarnell, Roger, "AREA AND VOLUME WHERE DO THE FORMULAS COME FROM?" (2016). Masters Essays. 33. http://collected.jcu.edu/mastersessays/33 This Essay is brought to you for free and open access by the Theses, Essays, and Senior Honors Projects at Carroll Collected. It has been accepted for inclusion in Masters Essays by an authorized administrator of Carroll Collected. For more information, please contact [email protected]. AREA AND VOLUME WHERE DO THE FORMULAS COME FROM? An Essay Submitted to the Office of Graduate Studies College of Arts & Sciences of John Carroll University In Partial Fulfillment of the Requirements For the Degree of Masters of Arts in Mathematics By Roger L Yarnell 2016 This essay of Roger L. Yarnell is hereby accepted: ________________________________________________ __________________ Advisor – Douglas Norris Date I certify that this is the original document ________________________________________________ __________________ Author – Roger L. Yarnell Date TABLE OF CONTENTS 1. Introduction 2 2. Basic Area Formulas 4 3. Pi and the Circle 10 4. Basic Volume Formulas 14 5. Sphere 17 6. Pythagorean Theorem 20 7. Conclusion 23 8. References 24 1 1. INTRODUCTION What are area and volume? This was a question that was posed to incoming geometry students that have previously worked with these measurements in middle school. There were a variety of responses to the question, how are area and volume defined? Approximately half of the students had a general idea of what area and volume measure.
    [Show full text]