Perimeter, Diameter and Area of Convex Sets in the Hyperbolic Plane
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Perimeter, Area, and Volume
Perimeter, Area, and Volume Perimeter is a measurement of length. It is the distance around something. We use perimeter when building a fence around a yard or any place that needs to be enclosed. In that case, we would measure the distance in feet, yards, or meters. In math, we usually measure the perimeter of polygons. To find the perimeter of any polygon, we add the lengths of the sides. 2 m 2 m P = 2 m + 2 m + 2 m = 6 m 2 m 3 ft. 1 ft. 1 ft. P = 1 ft. + 1 ft. + 3 ft. + 3 ft. = 8 ft. 3ft When we measure perimeter, we always use units of length. For example, in the triangle above, the unit of length is meters. For the rectangle above, the unit of length is feet. PRACTICE! 1. What is the perimeter of this figure? 5 cm 3.5 cm 3.5 cm 2 cm 2. What is the perimeter of this figure? 2 cm Area Perimeter, Area, and Volume Remember that area is the number of square units that are needed to cover a surface. Think of a backyard enclosed with a fence. To build the fence, we need to know the perimeter. If we want to grow grass in the backyard, we need to know the area so that we can buy enough grass seed to cover the surface of yard. The yard is measured in square feet. All area is measured in square units. The figure below represents the backyard. 25 ft. The area of a square Finding the area of a square: is found by multiplying side x side. -

Rectangles with the Same Numerical Area and Perimeter
Rectangles with the Same Numerical Area and Perimeter About Illustrations: Illustrations of the Standards for Mathematical Practice (SMP) consist of several pieces, including a mathematics task, student dialogue, mathematical overview, teacher reflection questions, and student materials. While the primary use of Illustrations is for teacher learning about the SMP, some components may be used in the classroom with students. These include the mathematics task, student dialogue, and student materials. For additional Illustrations or to learn about a professional development curriculum centered around the use of Illustrations, please visit mathpractices.edc.org. About the Rectangles with the Same Numerical Area and Perimeter Illustration: This Illustration’s student dialogue shows the conversation among three students who are trying to find all rectangles that have the same numerical area and perimeter. After trying different rectangles of specific dimensions, students finally develop an equation that describes the relationship between the width and length of a rectangle with equal area and perimeter. Highlighted Standard(s) for Mathematical Practice (MP) MP 1: Make sense of problems and persevere in solving them. MP 2: Reason abstractly and quantitatively. MP 7: Look for and make use of structure. MP 8: Look for and express regularity in repeated reasoning. Target Grade Level: Grades 8–9 Target Content Domain: Creating Equations (Algebra Conceptual Category) Highlighted Standard(s) for Mathematical Content A.CED.A.2 Create equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales. A.CED.A.4 Rearrange formulas to highlight a quantity of interest, using the same reasoning as in solving equations. -

Area and Perimeter What Is the Formula for Perimeter and How Is It Applied in Construction?
Name: Basic Carpentry Coop Tech Morning/Afternoon Canarsie HS Campus Mr. Pross Finding Area and Perimeter What is the formula for perimeter and how is it applied in construction? 1. Perimeter: The perimeter of a rectangle is the distance around it. Therefore, the perimeter is the sum of all four sides. Perimeter is important when calculating estimates for materials needed for completing a job. Example: Before ordering baseboard trim, the must wrap around the entire room, the perimeter of a 12’ 12 ft x 18 ft room must be found. What is the perimeter of the room? 18’ What is the formula for perimeter? Write it below. _______________________ 1. This is the formula you will need to follow in order to calculate area. = 2 (12 ft + 18 ft) 2. Add the length and width in parentheses. The length plus the width represent halfway around the room. = 2 (30 ft) 3. Multiply the sum of the length and width by 2 to find the entire distance around. = 60 ft. Practice A client asked that you to install a new window. The framing though is too small and you need to demolish it and rebuild it. First you need to find the perimeter of the window. If this window measures 32 inches by 42 inches, what is the perimeter? Name: Basic Carpentry Coop Tech Morning/Afternoon Canarsie HS Campus Mr. Pross 2. Area: The area of a square is the surface included within a set of lines. In carpentry, this means the total space of a room or even a building. Area, like permiter, is an important mathematical formula for estimating material and cost in construction. -

Perimeter , Area and Volume with Changed Dimensions
Perimeter , Area and Volume with changed dimensions Given a rectangle with dimensions of 6 by 4. Perimeter: __________ Area: ______________ Double the dimensions of the rectangle (multiply each side by 2) New Perimeter: ___________ New Area: _______________ Compare the effects on the perimeter and area when dimensions of a shape are changed (dilated) proportionally. Complete the chart below: Smaller Larger Ratio of larger Rectangle Rectangle dimension to smaller dimension Length Width Perimeter Area Conclusion: Perimeter , Area and Volume with changed dimensions If the dimensions of the rectangle are doubled (scale factor of 2): the perimeter is___________ If the dimensions of the rectangles are doubled (scale factor of 2): the area is ____________ Extension: If the dimensions of the rectangle are tripled (scale factor of 3): the perimeter is ______________ If the dimensions of the rectangle are triples (scale factor of 3): the area is ___________________ What do you think will happen to volume when dimensions are changed proportionally? Given a rectangular prism with dimensions of 6 by 4 by 2: Volume: _____________ Double the dimensions of the prism: New Volume: __________ Perimeter , Area and Volume with changed dimensions Smaller Rectangle Larger Rectangle Ratio of larger dimension to smaller dimension Length Width Height Volume Since each dimension was dilated (multiplied) by 2, then the volume was multiplied by 8: or 23 (scale factor cubed) Why do you think the volume is “cubed”? Perimeter , Area and Volume with changed dimensions Effects on perimeter, area and volume when dimensions of a shape are changed proportionally: Original Scale factor Perimeter Area Volume times 2 times 2=___ times 22=___ times 23=___ times 3 times 4 1 times 2 2 times 3 3 times 4 Examples: 1. -

1.7 Find Perimeter, Circumference, and Area
&IND 0ERIMETER #IRCUMFERENCE AND !REA 'OAL + &IND DIMENSIONS OF POLYGONS &/2-5,!3 &/2 0%2)-%4%2 0 !2%! ! !.$ 9OUR .OTES #)2#5-&%2%.#% # 3QUARE 2ECTANGLE SIDE LENGTH S LENGTH * AND WIDTH W 0 Ê{ÃÊ 0 ÊÓ*ÊzÓÜÊ ! Ê ÃÓÊ ! Ê *ÜÊ 4RIANGLE #IRCLE SIDE LENGTHS A B RADIUS R AND C BASE B # ÊÓ:ÀÊ AND HEIGHT H ! Ê :À ÓÊ 0 Ê >ÊzLÊzVÊ 0I : IS THE RATIO OF A £ ! ÊÊÊ]ÊÊÊL z Ê CIRCLEgS CIRCUMFERENCE TO Ó ITS DIAMETER %XAMPLE &IND THE PERIMETER AND AREA OF A RECTANGLE 4ENNIS 4HE IN BOUNDS PORTION OF A SINGLES TENNIS COURT IS SHOWN &IND ITS PERIMETER AND AREA 0ERIMETER !REA 0 * W ! *W ÊÇnÊ ÊÓÇÊ ÊÇnÊÊÓÇÊ ÊÓ£äÊ ÊÓ£äÈÊ 4HE PERIMETER IS ÊÓ£äÊ FT AND THE AREA IS ÊÓ£äÈÊ FT #HECKPOINT #OMPLETE THE FOLLOWING EXERCISE )N %XAMPLE THE WIDTH OF THE IN BOUNDS RECTANGLE INCREASES TO FEET FOR DOUBLES PLAY &IND THE PERIMETER AND AREA OF THE IN BOUNDS RECTANGLE ÊÊ«iÀiÌiÀ\ÊÓÓnÊvÌ]Ê>Ài>\ÊÓnänÊvÌÓ ,ESSON s 'EOMETRY .OTETAKING 'UIDE #OPYRIGHT Ú -C$OUGAL ,ITTELL(OUGHTON -IFFLIN #OMPANY 9OUR .OTES %XAMPLE &IND THE CIRCUMFERENCE AND AREA OF A CIRCLE !RCHERY 4HE SMALLEST CIRCLE ON AN /LYMPIC TARGET IS 4HE APPROXIMATIONS CENTIMETERS IN DIAMETER &IND THE APPROXIMATE AND ]zARE CIRCUMFERENCE AND AREA OF THE SMALLEST CIRCLE COMMONLY USED AS APPROXIMATIONS 3OLUTION FOR THE IRRATIONAL &IRST FIND THE RADIUS 4HE DIAMETER IS CENTIMETERS NUMBER : 5NLESS SO THE RADIUS IS ]zÊ£ÓÊ ÊÈÊ CENTIMETERS TOLD OTHERWISE USE FOR : 4HEN FIND THE CIRCUMFERENCE AND AREA 5SE FOR : 0 :R yzÊΰ£{Ê ÊÈÊ ÊÎÇ°ÈnÊVÊ ! :R yzÊΰ£{ÊÊÈÊ Ê££Î°ä{ÊVÓÊ #HECKPOINT &IND THE APPROXIMATE -
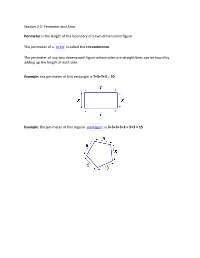
Section 2.2: Perimeter and Area
Section 2.2: Perimeter and Area Perimeter is the length of the boundary of a two dimensional figure. The perimeter of a circle is called the circumference. The perimeter of any two dimensional figure whose sides are straight lines can be found by adding up the length of each side. Example: the perimeter of this rectangle is 7+3+7+3 = 20 Example: the perimeter of this regular pentagon is 3+3+3+3+3 = 5×3 = 15 There are formulas that can help us find the perimeter of a few standard shapes. However, if a two dimensional shape has a border that consists of only straight lines simply adding up the lengths of each side will be sufficient to find the perimeter. I will need to use a formula to find the perimeter (circumference) of a circle as its border is not made of straight lines. Perimeter Formulas Triangle Perimeter = a + b + c Square Perimeter = 4 × a a = length of side Rectangle Perimeter = 2 × (w + h) Or 2(length + width) w = width h = height Quadrilateral Perimeter = a + b + c + d Circle Circumference = 2πr r = radius Example: Use the appropriate formula to find the perimeter of the rectangle below. I will use the formula: Perimeter = 2(length + width) It is customary to call the longer side of a rectangle the length. I will replace the length in the formula with 7 yards, and the width with 4 yards. Perimeter = 2(7 yards + 4 yards) = 2(11 yards) Answer: Perimeter = 22 yards (The units in a perimeter problem are linear and do not have squares.) Example: Find the circumference of the following circle. -

AREA and VOLUME WHERE DO the FORMULAS COME FROM? Roger Yarnell John Carroll University, [email protected]
John Carroll University Carroll Collected Masters Essays Theses, Essays, and Senior Honors Projects Spring 2016 AREA AND VOLUME WHERE DO THE FORMULAS COME FROM? Roger Yarnell John Carroll University, [email protected] Follow this and additional works at: http://collected.jcu.edu/mastersessays Part of the Geometry and Topology Commons Recommended Citation Yarnell, Roger, "AREA AND VOLUME WHERE DO THE FORMULAS COME FROM?" (2016). Masters Essays. 33. http://collected.jcu.edu/mastersessays/33 This Essay is brought to you for free and open access by the Theses, Essays, and Senior Honors Projects at Carroll Collected. It has been accepted for inclusion in Masters Essays by an authorized administrator of Carroll Collected. For more information, please contact [email protected]. AREA AND VOLUME WHERE DO THE FORMULAS COME FROM? An Essay Submitted to the Office of Graduate Studies College of Arts & Sciences of John Carroll University In Partial Fulfillment of the Requirements For the Degree of Masters of Arts in Mathematics By Roger L Yarnell 2016 This essay of Roger L. Yarnell is hereby accepted: ________________________________________________ __________________ Advisor – Douglas Norris Date I certify that this is the original document ________________________________________________ __________________ Author – Roger L. Yarnell Date TABLE OF CONTENTS 1. Introduction 2 2. Basic Area Formulas 4 3. Pi and the Circle 10 4. Basic Volume Formulas 14 5. Sphere 17 6. Pythagorean Theorem 20 7. Conclusion 23 8. References 24 1 1. INTRODUCTION What are area and volume? This was a question that was posed to incoming geometry students that have previously worked with these measurements in middle school. There were a variety of responses to the question, how are area and volume defined? Approximately half of the students had a general idea of what area and volume measure. -

The Story of Π
And of its friend e Wheels Colin Adams in the video “The Great π/e Debate” mentions the wheel “arguably the greatest invention of all times,” as an example of how π appeared already in prehistoric times. But square wheels are possible. If the surface of the earth were not flat but rilled in a very special way. For this to work each little rill (arc) has to have the shape of a hyperbolic cosine, a so called cosh curve. By definition, the hyperbolic cosine is ex e x coshx 2 Another appearance by e. As we shall see, π and e are closely related, even though the relationship is far from being well understood. NOTATION In these notes r = radius of a circle d= its diameter, d = 2r C = its circumference (perimeter) A = its area When did people discover that C A ? d r 2 The Story Begins… There are records (skeletons, skulls and other such cheerful remains) that indicate that the human species existed as long as 300,000 years ago. Most of this was prehistory. The following graph compares history to prehistory: The green part is prehistory, the red history. The vertical black line indicates the time to which some of the oldest records of human activity were dated. Ahmes, the scribe Scribes were a very important class in ancient Egypt. The picture shows a statue of a scribe. Ahmes, the scribe of the Rhind papyrus (c. 1650 BC) may have looked much like this guy. In the Rhind papyrus, Ahmes writes: Cut off 1/9 of a diameter and construct a square upon the remainder; this has the same area of the circle. -

CZU: 514.116 DOI: 10.36120/2587-3644.V8i2.43-50 the PROBLEM of the NUMBER Π and ANOTHER CONSTRUCTION of TRIGONOMETRY Sergiu
Acta et Coomentationes, Exact and Natural Sciences, nr. 2(8), 2019 ISSN 2537-6284 p. 43-50 E-ISSN 2587-3644 CZU: 514.116 DOI: 10.36120/2587-3644.v8i2.43-50 THE PROBLEM OF THE NUMBER π AND ANOTHER CONSTRUCTION OF TRIGONOMETRY Sergiu MIRON, dr. professor Chi¸sin˘au,Republic of Moldova Abstract. In this paper, the solution of the problem of the number π has been described. A definition of this number was formulated according to the model of the definition of the number e, mathematically well understood. Then this number was based on the definition of the length of the circle and of the arcs of the circle, and as well as on the definition of trigonometric functions of real variable. Keywords: number π, circle length, absolute trigonometry. PROBLEMA NUMARULUI˘ π S¸I ALTA˘ CONSTRUCT¸IE A TRIGONOMETRIEI Rezumat. ^In aceast˘alucrare se descrie rezolvarea problemei numarului π. S-a formulat definit¸ia acestui num˘ardup˘amodelul definit¸iei numarului e, bine inchegat˘adin punct de vedere matematic. Apoi acest numar a fost pus la baza definit¸iei lungimii cercului ¸siarcelor de cerc, precum ¸sila baza definit¸iei funct¸iilor trigonometrice de variabil˘areal˘a. Cuvinte-cheie: num˘arul π, lungimea cercului, trigonometria absolut˘a. 1. Introduction In this paper the oldest and most controversial mathematical problem in the history of mankind is studied. Thousands of years ago the barrels builders observed that between the length of the circle and its diameter there is a ratio that does not depend on the length of the diameter. This ratio today is known as the "number π". -

Finding Area, Perimeter, and Circumference
FINDING AREA, PERIMETER, AND CIRCUMFERENCE Area, perimeter, and circumference are all measures of two-dimensional shapes. These are things you can think of as flat: a football field, a piece of paper, or a pizza. You're probably not interested in how high they are, but you might want to know their: ● Perimeter or Circumference. This is the total length of a shape's outline. If you built a fence around its edge, how long would that fence be? If you walked around the edges of this area, how far would you have gone? The length of a straight-sided shape's outline is called its perimeter, and the length of a circle's outline is called its circumference. ● Area. This is the total amount of space inside a shape's outline. If you wanted to paint a wall or irrigate a circular field, how much space would you have to cover? Triangles 1. The perimeter of any triangle is the sum of its sides: a + b + c perimeter = a + b + c c 5 P = a + b + c a 3 P = 3 + 5 + 4 P = 12 b 4 2. The area of any triangle is half its base times its height. area = 1/2 bh A = 1/2 bh h 3 A = 1/2 * 3 * 4 A = 1/2 * 12 b 4 A = 6 It doesn't matter which of the triangle's short legs is the "base" and which is the "height": you get the same solution either way. A = 1/2 bh h 4 A = 1/2 * 4 * 3 A = 2 * 3 A = 6 b 3 Squares 1. -
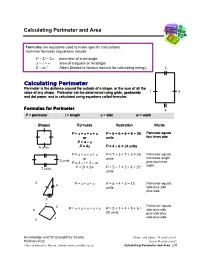
Calculating Perimeter and Area
Calculating Perimeter and Area Formulas are equations used to make specific calculations. Common formulas (equations) include: P = 2l + 2w perimeter of a rectangle A = l + w area of a square or rectangle 2 E = mc Albert Einstein’s famous formula for calculating energy. 2 Calculating Perimeter Perimeter is the distance around the outside of a shape, or the sum of all the sides of any shape. Perimeter can be determined using grids, geoboards 1 3 and dot paper, and is calculated using equations called formulas. Formulas for Perimeter 4 P = perimeter l = length s = side w = width Shapes Formulas Illustration Words P = s + s + s + s P = 6 + 6 + 6 + 6 = 24 Perimeter equals or units four times side. P = 4 × s 6 units P = 4s P = 4 × 6 = 24 units P = s + s + s + s P = 7 + 3 + 7 + 3 = 20 Perimeter equals or units two times length 3 units P = 2 × l + 2 × w plus two times width. 7 units P = 2l + 2w P = 2 × 7 + 2 × 3 = 20 units 5 Perimeter equals 4 P = s + s + s P = 5 + 4 + 3 = 12 units side plus side plus side. 3 2 Perimeter equals 3 P = s + s + s + s + s P = 2 + 3 + 4 + 5 + 6 = 5 side plus side 20 units plus side plus side plus side. 6 4 Knowledge and Employability Studio Shape and Space: Measurement: Mathematics Linear Measurement: ©Alberta Education, Alberta, Canada (www.LearnAlberta.ca) Calculating Perimeter and Area 1/8 Circumference The perimeter of a circle is called circumference. The formulas to calculate circumference are: C = πd and C = 2πr 10 m C = πd = 3.14 × 10 m = 31.4 m π = 3.14 c = circumference (the distance around the circle) r = radius (the distance from middle of circle to circumference) d = diameter (the distance across at the middle of the circle) Calculating Area Area is the space inside a flat, two-dimensional shape. -

ELLIPTIC INTEGRALS and SOME APPLICATIONS Jay Villanueva
ELLIPTIC INTEGRALS AND SOME APPLICATIONS Jay Villanueva Florida Memorial University 15800 NW 42nd Ave Miami, FL 33054 [email protected] 1. Introduction 1.1 How they arose – perimeter of an ellipse 1.2 Standard forms from Legendre, Jacobi, and Landen 2. Properties and examples 2.1 Evaluating integrals 2.2 Elliptic functions 3. Applications 3.1 Calculus 3.1.1 Perimeter of an ellipse 3.1.2 Arclength of a lemniscate 3.2 Physics 3.2.1 Finite-amplitude pendulum 3.2.2 Perihelion of Mercury 4. Conclusion References: 1. JW Armitage and WF Eberlein, 2006. Elliptic Functions. Cambridge University Press. 2. HM Kean and V Moll, 1997. Elliptic Curves. Cambridge University Press. 3. DF Lawden, 1989. Elliptic Functions and Applications. New York: Springer Verlag. 4. V Prasolov and Y Sovolyev, 1997. Elliptic Functions and Elliptic Integrals. Providence, RI: American Mathematical Society. 5. HE Rauch and A Lebowitz, 1973. Elliptic Functions, Theta Functions, and Riemann Surfaces. MD: Williams and Wilkins Co. 6. Schaum’s Outlines, 1996. Advanced Calculus. NY: McGraw-Hill. Elliptic integrals arose from the attempts to find the perimeter of an ellipse: 푥2 푦2 + = 1, 푥 = 푎 cos 휃, 푦 = 푏 sin 휃 푎2 푏2 푎 2휋 퐿 = 푑푠 = 2 √1 + 푦′2푑푥 = 1 + 푏2푐표푠2휃(−푎푠푛휃)푑휃, ∫ ∫−푎 ∫0 √ which last integral cannot be evaluated by elementary functions, viz., trigonometric, exponential, or logarithmic functions. The incomplete elliptic integral of the first kind is defined as 휙 푑휃 푢 = 퐹(푘, 휙) = ∫ , 0 < 푘 < 1, 0 √1−푘2푠푛2휃 where 휙 is the amplitude of 퐹(푘, 휙) or u, written 휙 = am 푢, and k is the modulus, 푘 = mod 푢.