DOCSLIB.ORG

Studies in Mathematics, Volume II. Euclidean Geometry Based on Ruler and Protractor Axioms

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Studies in Mathematics, Volume II. Euclidean Geometry Based on Ruler and Protractor Axioms DOCUMENT RESUME' ED 143 544 SE' 023 028 AUTHOR Curtis, Charles W.; And Others ' TIrLE Studies in Mathematics, Volume II. Euclidean Geometry Based on Ruler and Protractor Axioms. Second Reviged Edition.---, INSTITUTION Stanford Univ., Calif. School Mathematics Study , Group. SPONS AGENCY Rational Science Foundation, Washington, D. C. PUB DATE 61 -NOTE 185p.; For related documents, see SE 023 029-041 EDRS PRICE MF-$0.83 HC-$10.03 Plus Postage. DESCRIPTORS *Geometry; Inservice Education; *Instructional Materials; *Resource Materials; Secondary Eddcation; *Secondary School Mathematics;, Teacher Eddcation; *Teaching,Guides ; IDENTIFIERS *School Mathematics Study Group ABSTRACT These materials were developed to help high school teachers to become'fatiliar with the approach to tenth-grade Eu :lidean geometry which was adopted by the SchoolMathematics Study Group (SMSG). It is emphasized that the materialg are unsuitable as a high school textbook. Each document contains material too difficult for most high school students. It is assumed that teachers whostUdr- 0:he notes, have good backgrounds in axiomati'c geometry. In particular, some familiarity with Euclid's Elements is presuppose d4.Chapters include:(1) Historical 'Introduction; (2) Logic;(3) Toints,',Lines, and Plahes; (4) Real Numbers and the Ruler Axidm; 0) Separation in Planes, and in Space; (6) Angles 'and the PrOtractor Fostplates; (7) Congruence; (8) Parallelism; (9) Area; and (10) Circles and Spheres. (Ahthor/RH), *******************************************************,*I ************" Docume's acquired by ERIC include many informal-unp bliShed , * * materials'n6t available from other ,sources. ERIC Mak$esyery effort * * togobtain-the bept copy availableNevertheless, items ofmarginal. *, * reprod'ucibiiity are often encountered and this affec the quality * * of the microfiche and ha'rdcopy reprOTuctions,ERiaakes eiaifable, * ,* via the ERIC Document ReproductionSeruice,NEDES).:EDRS is not * responsible for the quality of the original document. Repro actions * * supplied'by EDRS ,are the best that can be made .from the ori§:nal. *************************************************************** ****** SCHOOL J S OEPARTMENT OF HEALTH MATHEMATICS EDUCATION & WELFARE NATIONAL INSTITUTE OF STUPY--GROU P EOUCAtiON BEEN AEPPe E N E,", RFCF ROM -E A 2P.' ON C.,,G, N , 1/' N C F h OP OP,N ONS :N, PE PPE ". ),. NS'Tt 'EOP En .. : `N a h1i ^v w STUDIES INMATHEMATICS' VOLUME II EuclideanGeolnetry Bcisklon Ruler and ProtractorAxioms (second revised edition) By CHARLES W. CURTIS, Universityof Wisconsin- PAUL H. DAUS, Univeriily Of California,Los Angeles ROBERT J: WALKER, NrrieLlUniversity _ PE R'.s1/ J",If) R-PPO'H.JrE SIISG . j ^,''( ''' I R EWE Ar1 "iv 1( 2 SCHOOL. MATHEMATICS STUDY GROUP 'STUDIES IN MATHEMATICS VOLUME SII ' r Euclidian Geometry Based on Miler 4 41, s and Protractor Axioms (second revised edition), By CHAkES -.-W. CURTIS,Ilitiverlity of Wisconsin PAUL H. DAUS; University of California., Los Angels , . ROBERT J. WALKER, Cornell University. e Written for tSCHOOL MATHEMATICS STUD'.CRoUP Under' a gra t from the NATIONAL SCIENCE FOUNDATION ti y . Copyright 1961 by Yale U iversity. 4.) 55 . ii PHA TOLITHOPRINT EU f1,Y CUSHING - MALLOY INC AN ARBOR MICHIGAN NITEU S YATES OF AMERICA **. Preface', These noteshave'been prepared tohelp high school teachers to become familiar with the, approach to tenth grade Euclidean geometry which has been adopted, by the School Mathematics Study 4 Group (SMSG).They are intended specificalto be used/during the summer of 1959,1 courses on geometry' for high school teachers. °A The 4M,SC1-,133preparing a tenth grade geometry text book anda 1 M teachers' manual, and these notes follow the preliminary outline of the `text book. It should be emphasized,- that these notes are , quite unsuitable as a text book for high school stUdents,' nor can they be used as a teachers manual. -They contain twin material ...which is too difficult to bt"presented to most tenth graders, but ,which we believe it is important for tenth grade t eachers to know. -,The'notes probe deeply into the beginni f thesubject,:brt do not'cover much of the material .of tandard tenth gradg-ieometry 'CR=26. In particular, the notes do nocover such topics as a parallels, circles, areas, Pythagorean theoreM, lytic geometry, etc., whereas all of these will be treatedin the SMSG text book. 0, ., - It.-.4.8 assumed that teachers who study these notes have good . \--/ . ' . I 'backgroundsin axiomatic geometry. In particular some familiarity ..k.... '. , with tuclidts Elements is presupposed, and the teachers should have access to these. (Heath's translation i Everyman's Lit'rary. (E.p. Dutton) is convenient.) .1rhenotee, oontai onfg occasional 1, . .t ). i '71° 4 r" - .4 references to the common high schooltreatments ofgeometry, but Ot the treaders should continually, make comparisons ofthe two types of treatment, especially the proofs of the More familiar theorems. Although we have tried to anticipate the content, order, notation, etc. of the proposed text book there is bound to be .ome divergent However, we are confidet that we are presenting the spirit of the new course; and that anyone who understands the . material these notes will be able to use the text book in an: intelligent and interesting manner. A instructor .in a summer ,course forteachers is urged tb spend most of theti me,onChapters4r 7. These contain the material on the Ruler and PrOtractor Axioms, and the theoryof separation or order Of 'points on a line, lines in a plane, and , planes in space.'Mtch of this, material is unfamiliar to riliky teacher*. Chapters 1 -'3 are introductory in nature, and can be covered . swiftly at the beginning, and referred to'fromtime to time as,the I'. course pr greSses...' / 0.4 ,These notes,are by no means a polished work, and it is: . ,- .:/ expebted that the . instructor will use good judgement indekding tr. 11 which'parts toam;Ify,which to light, what extramate*to flik : :i , 'put in, etc. Some exercises have been included but many additional *- k ,, 0 . ' : . ones will have to be Supplied. The starred theorems * ,(e.g. Theorem 3.1) can be 'used as exercises, and it is intended 1. - . P , that asman -,.aspossible .ofthese10 proved. Most of the early , - , , r "1? onep are used in later proofs, and their ommissionwould leave , 0 sriouB.,ga.rilit,,in the pryent.ation. 4 . i ne of our'proofs are accompaniedby diagrams. This was 'don partly to urge the reader to draw his owz diagram aid partly to emphasize that afOgical proof should be indepeindnt of any diagram.'Ieommission doed not mean that we \ wishtominimizetheimportanceof drawing -a figure to fix the" to ideas in the mind. The readers should make copatantme of diagrams as an aidto understanding tie theorems and discovering' proofs. 1 Future work byithe'SMSG on the text book, the teachers' . 'manual, and the teacher training, manual oan profit, greatly from comments,and,criticisms of these notes. You are 'urged to send 44: yo4r sftsgestions to School Mathematics Study Group::. ',Drawer 2502A Yale Station New Haven, Connecticut C- .7t t Tiii . 7 Prefa6eto Second Revision Several changevhave been made iii.this'edition to impiove the , material andbring it more into line with the text book., . 1. The notationsAtfor a line andABfor a distance have beeri adopted, On the other hand it did not seem 'worthwhile to change m( LATi.L)al ,mZABC and arcAB tO tN 2.'' The distance and separation postulates haVe been reworded to conforin to the text boat. However, tochaege the order of / 1 . presentation of these postulates to that used in theteXtbook . .-. would have necesgitated extensive alterations inChapters 3 and 4.. , ,-_____ The text bdokorder was dictated by pedagogical considerations, .1 p#inciPally the desire to avdict indirect Tiroof's intheifiist _ .). , .. , . theorems, which do not apply to this boor. It was the efore , . decided to leave the order as in the earlier editions. The . pottulate's thus differ in numbering as follows: These Notes. Textbook Incidence postulated 1, 2:3, 4, 5\ 1, .5,6", 7, 8 Distance ppsiulates 8. 2, 3, 4. e . I " '3. Chapters on Parallels ,and on Ares.', lave been', inserted to- f ':. clarify the position of these topics in oti.r presentation.. , _ _ _ __._ , .' r 4., Numerous minor'thanges, insertiond, corrections, etc,. have-been made, and one-significant error has been corrected (Section 4 of Chapter 5). 6 'iv -8 The user of this book', .71 find much additional material in the text book, including,si exercises'and expository material in the text book proper and lementary reading in-the Teachers, Commentary, the Appendices, an articularly the,Talks to Teachers In this book we present Eu can gedmetry as a mathematical theory. We havelett aside all, a ications of geometry to questions in physics-and to other wiles of mathematics. This is not to say that we regard these licatiorts as unimportant for the teacher to know and to use in the ,lassroom; in tact, it would be a mistake to teach geometry"to high' chool students without 1 bringing in some of the significant aPp cations, especially to elementary physics.The reader of this k ill find abundant_ supplementary material on applications of entary geometry in the following books: e G. Polya, Mathematics and kauiible/R Princeton University Press, vol. 1, especially the chapter on "Physical Mathematics1' R. Courant and H. Robbins, What is Mathematics ?, Oxford University Press. -N. H. Rademacher and 0. Toepljtz, The Enjoymentof Mathematics, Princeton University Press. II CONTENTS * * * * I Chapter Page 1. Historical Introduction 1 2. Logic 37 f 3. Points, Lines, and Planes . .. 63 4. Real Numbers and the Ruler Axiom 69 . 5. Separation in Planes and.in Space 107 6. Angles'and'the Protractor Postulates 115 7. Congruence .31. 8. Parallelism 1k5 9. Area 153 I . - 10. Circles and Spheres 169* 10 .4 "ot - -;,----- a Chapter 1 Historical Introduction 1. The Glory' that is Euclid's.
Load more

Recommended publications
  • Canada Archives Canada Published Heritage Direction Du Branch Patrimoine De I'edition
    Rhetoric more geometrico in Proclus' Elements of Theology and Boethius' De Hebdomadibus A Thesis submitted in Candidacy for the Degree of Master of Arts in Philosophy Institute for Christian Studies Toronto, Ontario By Carlos R. Bovell November 2007 Library and Bibliotheque et 1*1 Archives Canada Archives Canada Published Heritage Direction du Branch Patrimoine de I'edition 395 Wellington Street 395, rue Wellington Ottawa ON K1A0N4 Ottawa ON K1A0N4 Canada Canada Your file Votre reference ISBN: 978-0-494-43117-7 Our file Notre reference ISBN: 978-0-494-43117-7 NOTICE: AVIS: The author has granted a non­ L'auteur a accorde une licence non exclusive exclusive license allowing Library permettant a la Bibliotheque et Archives and Archives Canada to reproduce, Canada de reproduire, publier, archiver, publish, archive, preserve, conserve, sauvegarder, conserver, transmettre au public communicate to the public by par telecommunication ou par Plntemet, prefer, telecommunication or on the Internet, distribuer et vendre des theses partout dans loan, distribute and sell theses le monde, a des fins commerciales ou autres, worldwide, for commercial or non­ sur support microforme, papier, electronique commercial purposes, in microform, et/ou autres formats. paper, electronic and/or any other formats. The author retains copyright L'auteur conserve la propriete du droit d'auteur ownership and moral rights in et des droits moraux qui protege cette these. this thesis. Neither the thesis Ni la these ni des extraits substantiels de nor substantial extracts from it celle-ci ne doivent etre imprimes ou autrement may be printed or otherwise reproduits sans son autorisation. reproduced without the author's permission.
    [Show full text]
  • Section 2.1: Proof Techniques
    Section 2.1: Proof Techniques January 25, 2021 Abstract Sometimes we see patterns in nature and wonder if they hold in general: in such situations we are demonstrating the appli- cation of inductive reasoning to propose a conjecture, which may become a theorem which we attempt to prove via deduc- tive reasoning. From our work in Chapter 1, we conceive of a theorem as an argument of the form P → Q, whose validity we seek to demonstrate. Example: A student was doing a proof and suddenly specu- lated “Couldn’t we just say (A → (B → C)) ∧ B → (A → C)?” Can she? It’s a theorem – either we prove it, or we provide a counterexample. This section outlines a variety of proof techniques, including direct proofs, proofs by contraposition, proofs by contradiction, proofs by exhaustion, and proofs by dumb luck or genius! You have already seen each of these in Chapter 1 (with the exception of “dumb luck or genius”, perhaps). 1 Theorems and Informal Proofs The theorem-forming process is one in which we • make observations about nature, about a system under study, etc.; • discover patterns which appear to hold in general; • state the rule; and then • attempt to prove it (or disprove it). This process is formalized in the following definitions: • inductive reasoning - drawing a conclusion based on experi- ence, which one might state as a conjecture or theorem; but al- mostalwaysas If(hypotheses)then(conclusion). • deductive reasoning - application of a logic system to investi- gate a proposed conclusion based on hypotheses (hence proving, disproving, or, failing either, holding in limbo the conclusion).
    [Show full text]
  • History of Mathematics
    Georgia Department of Education History of Mathematics K-12 Mathematics Introduction The Georgia Mathematics Curriculum focuses on actively engaging the students in the development of mathematical understanding by using manipulatives and a variety of representations, working independently and cooperatively to solve problems, estimating and computing efficiently, and conducting investigations and recording findings. There is a shift towards applying mathematical concepts and skills in the context of authentic problems and for the student to understand concepts rather than merely follow a sequence of procedures. In mathematics classrooms, students will learn to think critically in a mathematical way with an understanding that there are many different ways to a solution and sometimes more than one right answer in applied mathematics. Mathematics is the economy of information. The central idea of all mathematics is to discover how knowing some things well, via reasoning, permit students to know much else—without having to commit the information to memory as a separate fact. It is the reasoned, logical connections that make mathematics coherent. The implementation of the Georgia Standards of Excellence in Mathematics places a greater emphasis on sense making, problem solving, reasoning, representation, connections, and communication. History of Mathematics History of Mathematics is a one-semester elective course option for students who have completed AP Calculus or are taking AP Calculus concurrently. It traces the development of major branches of mathematics throughout history, specifically algebra, geometry, number theory, and methods of proofs, how that development was influenced by the needs of various cultures, and how the mathematics in turn influenced culture. The course extends the numbers and counting, algebra, geometry, and data analysis and probability strands from previous courses, and includes a new history strand.
    [Show full text]
  • Can One Design a Geometry Engine? on the (Un) Decidability of Affine
    Noname manuscript No. (will be inserted by the editor) Can one design a geometry engine? On the (un)decidability of certain affine Euclidean geometries Johann A. Makowsky Received: June 4, 2018/ Accepted: date Abstract We survey the status of decidabilty of the consequence relation in various ax- iomatizations of Euclidean geometry. We draw attention to a widely overlooked result by Martin Ziegler from 1980, which proves Tarski’s conjecture on the undecidability of finitely axiomatizable theories of fields. We elaborate on how to use Ziegler’s theorem to show that the consequence relations for the first order theory of the Hilbert plane and the Euclidean plane are undecidable. As new results we add: (A) The first order consequence relations for Wu’s orthogonal and metric geometries (Wen- Ts¨un Wu, 1984), and for the axiomatization of Origami geometry (J. Justin 1986, H. Huzita 1991) are undecidable. It was already known that the universal theory of Hilbert planes and Wu’s orthogonal geom- etry is decidable. We show here using elementary model theoretic tools that (B) the universal first order consequences of any geometric theory T of Pappian planes which is consistent with the analytic geometry of the reals is decidable. The techniques used were all known to experts in mathematical logic and geometry in the past but no detailed proofs are easily accessible for practitioners of symbolic computation or automated theorem proving. Keywords Euclidean Geometry · Automated Theorem Proving · Undecidability arXiv:1712.07474v3 [cs.SC] 1 Jun 2018 J.A. Makowsky Faculty of Computer Science, Technion–Israel Institute of Technology, Haifa, Israel E-mail: [email protected] 2 J.A.
    [Show full text]
  • 20. Geometry of the Circle (SC)
    20. GEOMETRY OF THE CIRCLE PARTS OF THE CIRCLE Segments When we speak of a circle we may be referring to the plane figure itself or the boundary of the shape, called the circumference. In solving problems involving the circle, we must be familiar with several theorems. In order to understand these theorems, we review the names given to parts of a circle. Diameter and chord The region that is encompassed between an arc and a chord is called a segment. The region between the chord and the minor arc is called the minor segment. The region between the chord and the major arc is called the major segment. If the chord is a diameter, then both segments are equal and are called semi-circles. The straight line joining any two points on the circle is called a chord. Sectors A diameter is a chord that passes through the center of the circle. It is, therefore, the longest possible chord of a circle. In the diagram, O is the center of the circle, AB is a diameter and PQ is also a chord. Arcs The region that is enclosed by any two radii and an arc is called a sector. If the region is bounded by the two radii and a minor arc, then it is called the minor sector. www.faspassmaths.comIf the region is bounded by two radii and the major arc, it is called the major sector. An arc of a circle is the part of the circumference of the circle that is cut off by a chord.
    [Show full text]
  • SOME GEOMETRY in HIGH-DIMENSIONAL SPACES 11 Containing Cn(S) Tends to ∞ with N
    SOME GEOMETRY IN HIGH-DIMENSIONAL SPACES MATH 527A 1. Introduction Our geometric intuition is derived from three-dimensional space. Three coordinates suffice. Many objects of interest in analysis, however, require far more coordinates for a complete description. For example, a function f with domain [−1; 1] is defined by infinitely many \coordi- nates" f(t), one for each t 2 [−1; 1]. Or, we could consider f as being P1 n determined by its Taylor series n=0 ant (when such a representation exists). In that case, the numbers a0; a1; a2;::: could be thought of as coordinates. Perhaps the association of Fourier coefficients (there are countably many of them) to a periodic function is familiar; those are again coordinates of a sort. Strange Things can happen in infinite dimensions. One usually meets these, gradually (reluctantly?), in a course on Real Analysis or Func- tional Analysis. But infinite dimensional spaces need not always be completely mysterious; sometimes one lucks out and can watch a \coun- terintuitive" phenomenon developing in Rn for large n. This might be of use in one of several ways: perhaps the behavior for large but finite n is already useful, or one can deduce an interesting statement about limn!1 of something, or a peculiarity of infinite-dimensional spaces is illuminated. I will describe some curious features of cubes and balls in Rn, as n ! 1. These illustrate a phenomenon called concentration of measure. It will turn out that the important law of large numbers from probability theory is just one manifestation of high-dimensional geometry.
    [Show full text]
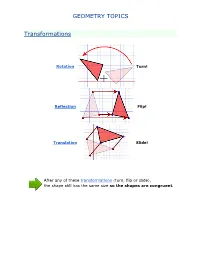
  • Geometry Topics
    GEOMETRY TOPICS Transformations Rotation Turn! Reflection Flip! Translation Slide! After any of these transformations (turn, flip or slide), the shape still has the same size so the shapes are congruent. Rotations Rotation means turning around a center. The distance from the center to any point on the shape stays the same. The rotation has the same size as the original shape. Here a triangle is rotated around the point marked with a "+" Translations In Geometry, "Translation" simply means Moving. The translation has the same size of the original shape. To Translate a shape: Every point of the shape must move: the same distance in the same direction. Reflections A reflection is a flip over a line. In a Reflection every point is the same distance from a central line. The reflection has the same size as the original image. The central line is called the Mirror Line ... Mirror Lines can be in any direction. Reflection Symmetry Reflection Symmetry (sometimes called Line Symmetry or Mirror Symmetry) is easy to see, because one half is the reflection of the other half. Here my dog "Flame" has her face made perfectly symmetrical with a bit of photo magic. The white line down the center is the Line of Symmetry (also called the "Mirror Line") The reflection in this lake also has symmetry, but in this case: -The Line of Symmetry runs left-to-right (horizontally) -It is not perfect symmetry, because of the lake surface. Line of Symmetry The Line of Symmetry (also called the Mirror Line) can be in any direction. But there are four common directions, and they are named for the line they make on the standard XY graph.
    [Show full text]
  • A CONCISE MINI HISTORY of GEOMETRY 1. Origin And
    Kragujevac Journal of Mathematics Volume 38(1) (2014), Pages 5{21. A CONCISE MINI HISTORY OF GEOMETRY LEOPOLD VERSTRAELEN 1. Origin and development in Old Greece Mathematics was the crowning and lasting achievement of the ancient Greek cul- ture. To more or less extent, arithmetical and geometrical problems had been ex- plored already before, in several previous civilisations at various parts of the world, within a kind of practical mathematical scientific context. The knowledge which in particular as such first had been acquired in Mesopotamia and later on in Egypt, and the philosophical reflections on its meaning and its nature by \the Old Greeks", resulted in the sublime creation of mathematics as a characteristically abstract and deductive science. The name for this science, \mathematics", stems from the Greek language, and basically means \knowledge and understanding", and became of use in most other languages as well; realising however that, as a matter of fact, it is really an art to reach new knowledge and better understanding, the Dutch term for mathematics, \wiskunde", in translation: \the art to achieve wisdom", might be even more appropriate. For specimens of the human kind, \nature" essentially stands for their organised thoughts about sensations and perceptions of \their worlds outside and inside" and \doing mathematics" basically stands for their thoughtful living in \the universe" of their idealisations and abstractions of these sensations and perceptions. Or, as Stewart stated in the revised book \What is Mathematics?" of Courant and Robbins: \Mathematics links the abstract world of mental concepts to the real world of physical things without being located completely in either".
    [Show full text]
  • Logic and Proof Release 3.18.4
    Logic and Proof Release 3.18.4 Jeremy Avigad, Robert Y. Lewis, and Floris van Doorn Sep 10, 2021 CONTENTS 1 Introduction 1 1.1 Mathematical Proof ............................................ 1 1.2 Symbolic Logic .............................................. 2 1.3 Interactive Theorem Proving ....................................... 4 1.4 The Semantic Point of View ....................................... 5 1.5 Goals Summarized ............................................ 6 1.6 About this Textbook ........................................... 6 2 Propositional Logic 7 2.1 A Puzzle ................................................. 7 2.2 A Solution ................................................ 7 2.3 Rules of Inference ............................................ 8 2.4 The Language of Propositional Logic ................................... 15 2.5 Exercises ................................................. 16 3 Natural Deduction for Propositional Logic 17 3.1 Derivations in Natural Deduction ..................................... 17 3.2 Examples ................................................. 19 3.3 Forward and Backward Reasoning .................................... 20 3.4 Reasoning by Cases ............................................ 22 3.5 Some Logical Identities .......................................... 23 3.6 Exercises ................................................. 24 4 Propositional Logic in Lean 25 4.1 Expressions for Propositions and Proofs ................................. 25 4.2 More commands ............................................
    [Show full text]
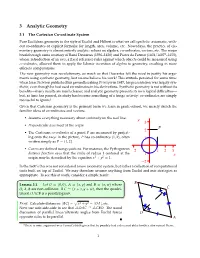
  • 3 Analytic Geometry
    3 Analytic Geometry 3.1 The Cartesian Co-ordinate System Pure Euclidean geometry in the style of Euclid and Hilbert is what we call synthetic: axiomatic, with- out co-ordinates or explicit formulæ for length, area, volume, etc. Nowadays, the practice of ele- mentary geometry is almost entirely analytic: reliant on algebra, co-ordinates, vectors, etc. The major breakthrough came courtesy of Rene´ Descartes (1596–1650) and Pierre de Fermat (1601/16071–1655), whose introduction of an axis, a fixed reference ruler against which objects could be measured using co-ordinates, allowed them to apply the Islamic invention of algebra to geometry, resulting in more efficient computations. The new geometry was revolutionary, so much so that Descartes felt the need to justify his argu- ments using synthetic geometry, lest no-one believe his work! This attitude persisted for some time: when Issac Newton published his groundbreaking Principia in 1687, his presentation was largely syn- thetic, even though he had used co-ordinates in his derivations. Synthetic geometry is not without its benefits—many results are much cleaner, and analytic geometry presents its own logical difficulties— but, as time has passed, its study has become something of a fringe activity: co-ordinates are simply too useful to ignore! Given that Cartesian geometry is the primary form we learn in grade-school, we merely sketch the familiar ideas of co-ordinates and vectors. • Assume everything necessary about on the real line. continuity y 3 • Perpendicular axes meet at the origin. P 2 • The Cartesian co-ordinates of a point P are measured by project- ing onto the axes: in the picture, P has co-ordinates (1, 2), often 1 written simply as P = (1, 2).
    [Show full text]
  • Synthetic and Analytic Geometry
    CHAPTER I SYNTHETIC AND ANALYTIC GEOMETRY The purpose of this chapter is to review some basic facts from classical deductive geometry and coordinate geometry from slightly more advanced viewpoints. The latter reflect the approaches taken in subsequent chapters of these notes. 1. Axioms for Euclidean geometry During the 19th century, mathematicians recognized that the logical foundations of their subject had to be re-examined and strengthened. In particular, it was very apparent that the axiomatic setting for geometry in Euclid's Elements requires nontrivial modifications. Several ways of doing this were worked out by the end of the century, and in 1900 D. Hilbert1 (1862{1943) gave a definitive account of the modern foundations in his highly influential book, Foundations of Geometry. Mathematical theories begin with primitive concepts, which are not formally defined, and as- sumptions or axioms which describe the basic relations among the concepts. In Hilbert's setting there are six primitive concepts: Points, lines, the notion of one point lying between two others (betweenness), congruence of segments (same distances between the endpoints) and congruence of angles (same angular measurement in degrees or radians). The axioms on these undefined concepts are divided into five classes: Incidence, order, congruence, parallelism and continuity. One notable feature of this classification is that only one class (congruence) requires the use of all six primitive concepts. More precisely, the concepts needed for the axiom classes are given as follows: Axiom class Concepts required Incidence Point, line, plane Order Point, line, plane, betweenness Congruence All six Parallelism Point, line, plane Continuity Point, line, plane, betweenness Strictly speaking, Hilbert's treatment of continuity involves congruence of segments, but the continuity axiom may be formulated without this concept (see Forder, Foundations of Euclidean Geometry, p.
    [Show full text]
  • Is Geometry Analytic? Mghanga David Mwakima
    IS GEOMETRY ANALYTIC? MGHANGA DAVID MWAKIMA 1. INTRODUCTION In the fourth chapter of Language, Truth and Logic, Ayer undertakes the task of showing how a priori knowledge of mathematics and logic is possible. In doing so, he argues that only if we understand mathematics and logic as analytic,1 by which he memorably meant “devoid of factual content”2, do we have a justified account of 3 a priori knowledgeδιανοια of these disciplines. In this chapter, it is not clear whether Ayer gives an argument per se for the analyticity of mathematics and logic. For when one reads that chapter, one sees that Ayer is mainly criticizing the views held by Kant and Mill with respect to arithmetic.4 Nevertheless, I believe that the positive argument is present. Ayer’s discussion of geometry5 in this chapter shows that it is this discussion which constitutes his positive argument for the thesis that analytic sentences are true 1 Now, I am aware that ‘analytic’ was understood differently by Kant, Carnap, Ayer, Quine, and Putnam. It is not even clear whether there is even an agreed definition of ‘analytic’ today. For the purposes of my paper, the meaning of ‘analytic’ is Carnap’s sense as described in: Michael, Friedman, Reconsidering Logical Positivism (New York: Cambridge University Press, 1999), in terms of the relativized a priori. 2 Alfred Jules, Ayer, Language, Truth and Logic (New York: Dover Publications, 1952), p. 79, 87. In these sections of the book, I think the reason Ayer chose to characterize analytic statements as “devoid of factual” content is in order to give an account of why analytic statements could not be shown to be false on the basis of observation.
    [Show full text]