Optically Controlling the Emission Chirality of Microlasers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2020Annual Report
2020 Annual Report DEAR FRIENDS With the Coronavirus national emergency declaration, Northern Illinois Hospice’s priorities shifted. Leadership pivoted and narrowed its scope to worldwide pandemic infection control and keeping patients and staff safe. By April 2020, the first individual with both a terminal diagnosis and COVID-19 was admitted. Now, more than 400 days have passed and COVID-19 has become an unwanted, extended guest of the American experience. Northern Illinois Hospice continues to be diligent with its emergency management efforts. Our team has done an amazing job, demonstrating the commitment, expertise, and quality and safety practices for which we are known. Beyond COVID-19, additionally last year: • A Paycheck Protection Program (PPP) Loan was secured, which helped with payroll for several weeks during the peak of the pandemic, and Health and Human Services (HHS) stimulus funds were received to offset COVID-related expenses. • A Capital Improvement Fund was established to From left: Northern Illinois Hospice Chief Executive plan for future needs of our building. The Fund’s first Officer Lisa Novak and Board of Directors President Jon Aldrich priority was to replace the old, worn out roof. • The Board of Directors unanimously voted to expand into DeKalb County, increasing Northern Illinois Hospice’s service area from five counties to six. This mission expansion currently is underway. • Community outreach continued, and we partnered with organizations like the Alzheimer’s Association to present webinars tailored to individuals caring for seriously ill loved ones at home. We also teamed up with local nursing and assisted living facilities to offer events like Puppy Parades to bring joy to socially-isolated residents. -
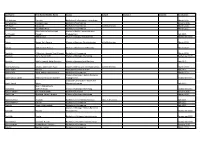
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation
Last Name First Name/Middle Name Course Award Course 2 Award 2 Graduation A/L Krishnan Thiinash Bachelor of Information Technology March 2015 A/L Selvaraju Theeban Raju Bachelor of Commerce January 2015 A/P Balan Durgarani Bachelor of Commerce with Distinction March 2015 A/P Rajaram Koushalya Priya Bachelor of Commerce March 2015 Hiba Mohsin Mohammed Master of Health Leadership and Aal-Yaseen Hussein Management July 2015 Aamer Muhammad Master of Quality Management September 2015 Abbas Hanaa Safy Seyam Master of Business Administration with Distinction March 2015 Abbasi Muhammad Hamza Master of International Business March 2015 Abdallah AlMustafa Hussein Saad Elsayed Bachelor of Commerce March 2015 Abdallah Asma Samir Lutfi Master of Strategic Marketing September 2015 Abdallah Moh'd Jawdat Abdel Rahman Master of International Business July 2015 AbdelAaty Mosa Amany Abdelkader Saad Master of Media and Communications with Distinction March 2015 Abdel-Karim Mervat Graduate Diploma in TESOL July 2015 Abdelmalik Mark Maher Abdelmesseh Bachelor of Commerce March 2015 Master of Strategic Human Resource Abdelrahman Abdo Mohammed Talat Abdelziz Management September 2015 Graduate Certificate in Health and Abdel-Sayed Mario Physical Education July 2015 Sherif Ahmed Fathy AbdRabou Abdelmohsen Master of Strategic Marketing September 2015 Abdul Hakeem Siti Fatimah Binte Bachelor of Science January 2015 Abdul Haq Shaddad Yousef Ibrahim Master of Strategic Marketing March 2015 Abdul Rahman Al Jabier Bachelor of Engineering Honours Class II, Division 1 -
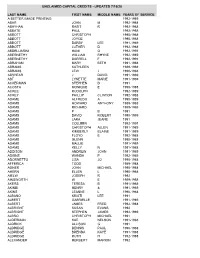
Last Name First Name Middle Name Years of Service A
UNCLAIMED CAPITAL CREDITS - UPDATED 7/16/20 LAST NAME FIRST NAME MIDDLE NAME YEARS OF SERVICE A BETTER IMAGE PRINTING 1992-1989 ABAR JOHN M 1992-1988 ABAYHAN RASIT R 1992-1988 ABBATE PAUL 1992-1988 ABBOTT CHRISTOPH 1990-1988 ABBOTT JOYCE 1990-1988 ABBOTT DARBY LEE 1991-1989 ABBOTT LUTHER D 1992-1988 ABDELUARIM HANI O 1992-1991 ABERNETHY WILLIAM RHYNE 1992-1989 ABERNETHY DARRELL F 1992-1991 ABRAHAM MARY BETH 1991-1988 ABRAMS KATHLEEN 1989-1988 ABRAMS LEW J 1990-1988 ABSHEAR J DAVID 1991-1989 ABT LYNETTE MARIE 1991-1989 ACKERMAN STEPHEN D 1991 ACOSTA MONIQUE E 1990-1988 ACREE RUDOLPH 1992-1989 ACREY PHILLIP CLINTON 1992-1988 ADAME ALFREDO A 1990-1989 ADAMS HOWARD ANTHONY 1989-1988 ADAMS RICHARD 1989-1988 ADAMS P B 1991 ADAMS DAVID ROBERT 1990-1989 ADAMS LARA JEANE 1991 ADAMS COLLEEN 1992-1991 ADAMS CHRISTOPH ALLEN 1991-1989 ADAMS KIMBERLY ELAINE 1991-1989 ADAMS FLOYD E 1992-1988 ADAMS GLENN 1990-1988 ADAMS MALLIE 1991-1989 ADAMS KELLY N 1991-1988 ADDISON ANDREW JOHN 1991-1989 ADKINS WANDA P 1992-1989 ADORNETTO LISA JO 1990-1988 AFFERICA TODD 1989-1988 AGNER JOHN MICHAEL 1990-1988 AHERN ELLEN L 1990-1988 AIELW JOSEPH R 1992 AINSWORTH W E 1989-1988 AKERS TERESA B 1991-1988 AKINBI HENRY & 1991-1989 AKINS LEANNE L 1990-1988 ALBANO KRISTI LEE 1991 ALBERT GABRIELLE 1991-1989 ALBERT JAMES FRED 1992-1988 ALBRIGHT SUSAN EVANS 1992 ALBRIGHT STEPHEN JAMES 1992-1989 ALBRO CHRISTOPH MICHAEL 1991 ALDERMAN KAE NELSON 1991-1988 ALDRICK ALLISON G 1991 ALDRIDGE DENNIS PAUL 1990-1988 ALDRIDGE BRENDA KAYE 1991-1988 ALDRIDGE RUTH H 1992-1988 ALEXANDER HERBERT -

Open Amber Lambert Dissertation
The Pennsylvania State University The Graduate School College of Education WOMEN IN ENGINEERING: THE GENDERED EFFECTS OF PROGRAM CHANGES, FACULTY ACTIVITIES, AND STUDENT EXPERIENCES ON LEARNING A Dissertation in Higher Education Administration by Amber D. Lambert © 2008 Amber D. Lambert Submitted in Partial Fulfillment of the Requirements for the Degree of Doctor of Philosophy May 2008 ii The thesis of Amber D. Lambert was reviewed and approved* by the following: Patrick T. Terenzini Distinguished Professor of Higher Education Dissertation Adviser Chair of Committee Lisa R. Lattuca Associate Professor of Higher Education Duane F. Alwin McCourtney Professor of Sociology Gül Kremer Affiliate Faculty of Industrial Engineering Assistant Professor of Engineering Design Dorothy Evensen Professor of Education In Charge of the Graduate Program in Higher Education *Signatures are on file in the Graduate School. iii Abstract Creating gender equity in engineering education is important for more reasons than simply being a matter of social justice or diversifying the engineering field. It is also a significant educational and public policy issue that will affect the future economic competitiveness of the United States in the global marketplace. Engineering is arguably the leading national example of a profession in which women are under-represented. Undergraduate engineering programs not only need to attract and retain female students, but they must also provide full access to the educational experiences women must have to develop the engineering skills to succeed in the engineering profession. This study explored whether the shift to the “soft” or less technical skills in engineering encouraged by new accreditation standards could potentially have had differential effects for women in engineering from their male counterparts. -

H Peschianna
H □ PESCHIANNA Foreword Once again as the door closes on another school year at Hopedale High, we look bock to a year full of both sod and happy memories. For the Freshmen it opened the door to a bright new world. For the Sophomores and Juniors the year was full of work and gay times. For the Seniors it is the final "good bye". But for all it is the end of another year. So these memories will not be lost or forgotten, the Hopeschianno has attempted to capture and record these memories. It can serve as the key in later years as we look through it, to open the door of our memories of that delightful year at Hopedale High in 1958-59. HOPEDALE HIGH SCHOOL Hopedale, Ohio HOPESCHIANNA Hopeschianna Pub Iished By SEN IOR CLASS HOPEDALE HIGH SCHOOL FACULTY ADVISOR: Lester A. Hickman Staff EDITOR: .•..••..••..••.••. Kay Stringer PHOTOGRAPHERS ••. .Chuck Marinacci Assistant Editor • • •. • ••••. Shirley Carman . .•• •• Bernard Kuryn SECRET ARY •. ....••.•• Joanne Murdock TYPISTS .•• . .•••••••••• Carol Pizzino PR OP HETS .• . •.•...•• . .•••Peggy Kenton ••.•.• •••• •. Joyce Davenport ••.••.••• •••. Jeannie Penoyer •• . •. ••.••. • ••.•• ••• Lois Ash SALES MANAGERS ..••••••• Gary Voich ROOM ED ITOR .••• • .•••• David Cox .••..• Ronnie Carlon SPORTS EDITOR ..••.•••• . • Rich Rensi ADVERTIZING: •.•..••.•• Larry Wohnhas ACTIV ITI ES ED ITOR •••• Eddie Pizzino MANAGERS •••• • •••• Gordon Ligget HISTORIAN .•••.••••• .•• Robert Black 4 this annual, . We, the da" af 1959o~ ieldedicate Ca,de,, _who h""as soaf pat1enth;gh - Hopesch,anna, h our junior an ly gu1'ded . us througto M r • . d senior ye school . 6 Hopedale Local School District LESTER A . HICKMAN, Superintendent Hopedale, Ohio Board of Education To the Members of the Graduating C lass of 1959: Th is letter comes to you with my warmest congratulations for a job we 11 done. -

1900 to 1956 Compiled by Janet Guida Denver, Colorado 2000
William P. Horan Burial Records - Index 1900 to 1956 Compiled by Janet Guida Denver, Colorado 2000 TABLE OF CONTENTS PREFERENCE ................................................................. iii A ....................................................................................................................... 1 B ..................................................................................................................... 13 C ..................................................................................................................... 55 D ..................................................................................................................... 98 E ................................................................................................................... 128 F ................................................................................................................... 136 G .................................................................................................................. 156 H .................................................................................................................. 182 I .................................................................................................................... 214 J ................................................................................................................... 216 K .................................................................................................................. 224 L .................................................................................................................. -

Is Your Name on This List?
Is your name on this list? The following individuals have not renewed their certification and may lose their designation if they do not renew in 2009: Alaska Daniela Takacs, CLT Alabama Alex Langford, CTP Blaine J. Guidry, CTP Brian K. Moseley, COLP, CTP Chris Agnew, CTP Chris Hildreth, CTP Chris Hogue, CTP David Billie, CTP Don Cotton, CTP Donald Rolin, CTP Frederick J. Emehiser, CTP Jeff Andrews, CTP John W. Richardson, CTP Larry Tranum, CTP Michael P. Smith, CTP Monica M. Rose, CTP Noel T. Cowart, CTP Phillip Naylor, CTP Roger Higgins, CTP Ronnie Browning, CTP Samuel Blevins, CTP Scott Key, CTP Terry Cook, CTP Tim Nix, CTP Tim Sullivan, CTP Tony Ivey, CTP Troy Trimm, CTP William Nowell, CTP Arkansas Adrienne DeBlock, CLT Bradley Lawson, CLT Carla Allen, CLT Charlotte Canfield, CLT David Maxwell, CTP Debbie Porter, CLP Derek Lipe, CLT Derrell Cox, CLT Don West, COLP Donghoon Lee, CTP Edna Mashburn, CLT Gayle A. Carrington, CLT Greg Jones, CLT Jack Bowen, CLP Jessica Otts, CLT Julia Fields, CLT Kathleen Pyeatt, CLT Kathy Gunter, CLT Kenneth Sawyer, CTP Kyle Wagner, CTP Matt Howard, CLT Michael Cunningham, CLT Phillip Hughes, CTP Rayla Ackerman, CLT Richard Bernard, CTP Richard Whitbeck, CTP Rusty Rippee, CTP Ruth Hill, CLT Sarah Smith, CLT Sean Conway, CLT Sean Williams, CTP Stephen Lars Jensen, CTP William Montes, CTP Arizona Alan Siebert, CTP David W. Pratt, CTP Dennis L. Kemp, CTP Gilbert Sanchez, CTP Jeanette Kline, CTP Jeffrey A. Fritsch, CTP Judy A. George, CLT Ken Vonderscher, CTP Lawrence Polk, CTP Leslie Shipley, CLP Luis Huizar, CLT Mark Janz, CTP Michael McIntyre, CLT Paul Ford, CLT Ray Keenan, COLP Raymond L. -

Bibno First Name Last Name City State Gender Age Chip Time Chip
BibNo First Name Last Name City State Gender Age Chip Time Chip Pace 2 Christian Hesch Hollywood CA M 33 1:06:37 5:06 6 Aissa Oghoughi Vancouver WA M 0 1:07:05 5:08 1 Mario Mendoza Bend OR M 26 1:08:53 5:16 7 Jason Griffiths Portland OR M 31 1:08:55 5:16 1116 Jacob Goertz Oregon CityOR M 22 1:11:08 5:26 3 Eric Griffiths Portland OR M 30 1:11:10 5:26 4 Charles Sunderlage Bellingham WA M 31 1:11:13 5:27 141 Kyle Baltrusch Portland OR M 25 1:15:16 5:45 1161 Eric Frome Portland OR M 31 1:16:27 5:51 158 Andy Bednarek Eugene OR M 29 1:18:06 5:58 16 Natalie Bak Bend OR F 27 1:19:23 6:04 19 Lauren Johnson Portland OR F 33 1:19:31 6:05 979 Roger Stevens Beaverton OR M 42 1:19:41 6:05 21 Korina Pongracz-BarthaPortland OR F 27 1:21:53 6:15 18 Lauren Breihof Redmond WA F 23 1:22:23 6:18 2106 Josh Platt Tigard OR M 21 1:24:32 6:28 15 Carre Heineck Portland OR F 30 1:24:46 6:29 823 Cesare Pozzi Mariano Comense M 40 1:24:48 6:29 262 John Clifford Sherwood OR M 50 1:24:49 6:29 1065 Brendan Wentz Sierra VistaAR M 29 1:26:01 6:34 1148 Michelle Hurn Portland OR F 29 1:26:15 6:36 1037 Charles Vazac San FranciscoCA M 34 1:26:21 6:36 190 David Boys Newport OR M 45 1:26:29 6:37 327 Jon Dotson Newberg OR M 48 1:26:31 6:37 2128 Rebecca Swinney Portland OR F 34 1:26:51 6:38 941 Luis Smith Marysville WA M 27 1:27:54 6:43 679 Tyler Martin Newberg OR M 39 1:28:09 6:44 1203 Eduardo Sandoval Seattle WA M 37 1:28:19 6:45 2189 Gilduin Barre Hillsboro OR M 44 1:28:30 6:46 2107 Chris Wolff Tigard OR M 49 1:28:32 6:46 439 Melissa Grelli Portland OR F 26 1:28:46 6:47 731 -

Poorhouse Admissions 1800-1858
Poorhouse Admissions 1800-1858 Last Name First Name Age Race Place of Residence Action taken by Directors Date Notes Bk/Pg Absolom 50 Black Dismissed or discharged 09/30/1802 1/7 Amelia Negro Chester County Poor H 05/11/1818 mother Ruth 1/116 Ann Black New Garden 12/25/1805 1/19 Anthony 3 Black 06/28/1807 1/24 Anthony Black Died in poor house or deceased 11/15/1808 error 1/29 Anthony 3 Black Died in poor house or deceased 1807 1/26 Bess 21 Negro Uwchlan Dismissed or discharged 04/27/1801 1/5 Betsy Black Bound, apprenticed, by a master 1814 M Isaac Pennock 1/76 Betty 3 Negro 08/15/1803 1/7 Betty 4 Negro Bound, apprenticed, by a master 1804 M James Andrews, UOxf 1/12 Bill Black Downingtown Supported in the poor house 11/04/1843 4/23 Bristo 103 Negro West Nantmeal Aided or assisted out of the poor house 12/22/1818 1/119 Bristo 103 Negro Aided or assisted out of the poor house 1820 1/132 Bristoe 103 Negro Aided or assisted out of the poor house 1819 in WNtm 1/120 Bristoe Negro Aided or assisted out of the poor house 1821 1/147 Bristoe Negro Aided or assisted out of the poor house 1822 1/166 Bristoe 100 Negro West Nantmeal Aided or assisted out of the poor house 1823 1/183 Charity 4m Black Kennett 12/10/1818 1/118 Charity 4m Black Died in poor house or deceased 1819 1/123 child Child Colored Pennsbury An order to bring in 11/05/1853 4/234 child Child Colored Dismissed or discharged 12/01/1853 taken out by her father 4/235 Cudjo 75 Negro East Nantmeal 01/14/1820 slave 1/139 Cudjo 100 Negro West Whiteland 12/28/1808 1/33 Cudjo 101 Negro Died -

Author Index (Print)
PHYSICAL REVIEW E VOLUME 57, NUMBER 4 APRIL 1998 Cumulative Author Index All authors of papers published so far in the current volume are listed alphabetically with the issue and page numbers following the dash. A more complete index, with the full title listed with each first author’s name and subsequent authors cross-referenced, is published in the last issue of the volume. A cumulative author and subject index covering Physical Review A through E, Physical Review Letters, and Reviews of Modern Physics is published annually under separate cover. Aafif, Amal—~2! 2471 A˚ stro¨m, Jan—~2! R1259 Bideau, D.—~4! 4743 Abel, M.—~3! 2820 Aswal, V. K.—~1! 776 Bideau, Daniel—~2! 1886; ~3! 3656 Abramson, Guillermo—~4! 4572 Ausloos, M.—~1! 1167 Biferale, L.—~3! R2515 Achrayah, R.—~4! 4361 Avery, P. R.—~1! 1193 Biktashev, V. N.—~3! 2656 Adler, P. M.—~4! 4466 Axna¨s, I.—~4! 4638 Biktasheva, I. V.—~3! 2656 Afanasjev, V. V.—~1! 1088 Billia, B.—~3! 2849 Agayan, V. A.—~1! 582; ~2! 1946 Baake, E.—~1! 1191 Billing, M.—~1! 1193 Agmon, Noam—~4! 3937 Baake, M.—~1! 1191 Binder, K.—~1! 1205~E!; ~2! 2425 Ågren, Hans—~4! 4778 Back, C. A.—~4! 4650 Binder, Kurt—~1! 843 Agudov, N. V.—~3! 2618 Badirkhan, Z.—~1! 460 Bird, C. M.—~3! 2787 Aguirre, M. A.—~4! 4743 Bahr, Ch.—~2! R1235 Birman, Joseph L.—~3! 3574 Ahlers, Guenter—~1! 638 Balkovsky, E.—~2! R1231 Biscarini, F.—~3! R2519 Ahuja, Rajeev—~2! 1673 Balschun, B.—~1! 720 Bisch, Paulo M.—~3! R2535 Akhmediev, N. -

2007-2008, Covering the Period July 1, 2007 Through June 30, 2008
Message from the President Dear Friends, There was much to celebrate during this past year at Marywood University. From a personal perspective, it was a transformative experience to serve my inaugural year as Marywood’s 11th president. However, I do not and could not do this alone. While this special year has provided an exciting backdrop, the meaningful role that each of you plays in shaping the future of this University is the underpinning of what continues to inspire and create our outstanding progress. In keeping with the spirit of progress, we decided this year to produce a “green” President’s Report— a solely online piece—to reduce our use of paper products and take another positive step in our ongoing efforts to cultivate and practice environmental stewardship. According to The Chronicle of Higher Education, “institutions of higher education are poised to play a leading role in developing and executing climate-neutral policies.” (“A Green Curriculum Involves Everyone on the Campus,” by John Peterson, June 20, 2008 issue) Marywood University continues to evaluate its current practices and engage in future initiatives with environmental considerations in mind—for the benefit of our students, our campus, our community, and our world. This report represents the fiscal year 2007-2008, covering the period July 1, 2007 through June 30, 2008. Please accept my deepest appreciation for all you have done to advance the goals, initiatives, and mission of Marywood University. I am enthusiastic about the progress we have made, as well as the momentum we continue to generate, and I look to our future with great optimism and abundant hope. -

Last Name First Name Birth Yrfather's Last Name Father's
Last Name First Name Birth YrFather's Last Name Father's First Name Mother's Last Name Mother's First Name Gender Aaron 1907 Aaron Benjaman Shields Minnie M Aaslund 1893 Aaslund Ole Johnson Augusta M Aaslund (Twins) 1895 Aaslund Oluf Carlson Augusta F Abbeal 1906 Abbeal William A Conlee Nina E M Abbitz Bertha Dora 1896 Abbitz Albert Keller Caroline F Abbot 1905 Abbot Earl R Seldorff Rose F Abbott Zella 1891 Abbott James H Perry Lissie F Abbott 1896 Abbott Marion Forder Charolotta M M Abbott 1904 Abbott Earl R Van Horn Rose M Abbott 1906 Abbott Earl R Silsdorff Rose M Abercrombie 1899 Abercrombie W Rogers A F Abernathy Marjorie May 1907 Abernathy Elmer Scott Margaret F Abernathy 1892 Abernathy Wm A Roberts Laura J F Abernethy 1905 Abernethy Elmer R Scott Margaret M M Abikz Louisa E 1902 Abikz Albert Keller Caroline F Abilz Charles 1903 Abilz Albert Keller Caroline M Abircombie 1901 Abircombie W A Racher Allos F Abitz Arthur Carl 1899 Abitz Albert Keller Caroline M Abrams 1902 Abrams L E Baker May F Absher 1905 Absher Ben Spillman Zoida M Achermann Bernadine W 1904 Ackermann Arthur Krone Karolina F Acker 1903 Acker Louis Carr Lena F Acker 1907 Acker Leyland Ryan Beatrice M Ackerman 1904 Ackerman Cecil Addison Willis Bessie May F Ackermann Berwyn 1905 Ackermann Max Mann Dolly M Acklengton 1892 Achlengton A A Riacting Nattie F Acton Rebecca Elizabeth 1891 Acton T M Cox Josie E F Acton 1900 Acton Chas Payne Minnie M Adair Elles 1906 Adair Adel M Last Name First Name Birth YrFather's Last Name Father's First Name Mother's Last Name Mother's