1 Mean Estimate Distances for Galaxies with Multiple
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Messier Objects
Messier Objects From the Stocker Astroscience Center at Florida International University Miami Florida The Messier Project Main contributors: • Daniel Puentes • Steven Revesz • Bobby Martinez Charles Messier • Gabriel Salazar • Riya Gandhi • Dr. James Webb – Director, Stocker Astroscience center • All images reduced and combined using MIRA image processing software. (Mirametrics) What are Messier Objects? • Messier objects are a list of astronomical sources compiled by Charles Messier, an 18th and early 19th century astronomer. He created a list of distracting objects to avoid while comet hunting. This list now contains over 110 objects, many of which are the most famous astronomical bodies known. The list contains planetary nebula, star clusters, and other galaxies. - Bobby Martinez The Telescope The telescope used to take these images is an Astronomical Consultants and Equipment (ACE) 24- inch (0.61-meter) Ritchey-Chretien reflecting telescope. It has a focal ratio of F6.2 and is supported on a structure independent of the building that houses it. It is equipped with a Finger Lakes 1kx1k CCD camera cooled to -30o C at the Cassegrain focus. It is equipped with dual filter wheels, the first containing UBVRI scientific filters and the second RGBL color filters. Messier 1 Found 6,500 light years away in the constellation of Taurus, the Crab Nebula (known as M1) is a supernova remnant. The original supernova that formed the crab nebula was observed by Chinese, Japanese and Arab astronomers in 1054 AD as an incredibly bright “Guest star” which was visible for over twenty-two months. The supernova that produced the Crab Nebula is thought to have been an evolved star roughly ten times more massive than the Sun. -

Science Discovery with Diverse Multi-Wavelength Data Fused in NED Joseph Mazzarella Caltech, IPAC/NED
Science Discovery with Diverse Multi-wavelength Data Fused in NED Joseph Mazzarella Caltech, IPAC/NED NED Team: Ben Chan, Tracy Chen, Cren Frayer, George Helou, Scott Terek, Rick Ebert, Tak Lo, Barry Madore, Joe Mazzarella, Olga Pevunova, Marion Schmitz, Ian Steer, Cindy Wang, Xiuqin Wu 7 Oct 2019 ADASS XXIX Groningen 1 Intro & outline Astro data are growing at an unprecedented rate. Ongoing expansion in volume, velocity and variety of data is creating great challenges, and exciting opportunities for discoveries from federated data. Advances in joining data across the spectrum from large sky surveys with > 100,000 smaller catalogs and journal articles, combined with new capabilities of the user interface, are helping astronomers make new discoveries directly from NED. This will be demonstrated with a tour of exciting scientific results recently enabled or facilitated by NED. Some challenges and limitations in joining heterogeneous datasets Outlook for the future 2 Overview: NED is maintaining a panchromatic census of the extragalactic Universe NED is: Published: • Linked to literature • Names • A synthesis of multi- and mission archives • (α,δ) wavelength data • Accessible via VO • Redshifts • D • Published data protocols Mpc • Easy-to-use • Fluxes augmented with • Sizes • Comprehensive derived physical • Attributes attributes • Growing rapidly • References • Notes Contributed: NED simplifies and accelerates • Images NED contains: • Spectra • 773 million multiwavelength cross-IDs scientific research on extragalactic • 667 million distinct objects Derived: • 4.9 billion photometric data points objects by distilling and synthesizing • Distances • 47 million object links to references data across the spectrum, and • Metric sizes SEDs • 7.9 million objects with redshifts providing value-added derived • Luminosities Aλ • 2.5 million images • Velocity corrections • And more .. -

Astronomy 2008 Index
Astronomy Magazine Article Title Index 10 rising stars of astronomy, 8:60–8:63 1.5 million galaxies revealed, 3:41–3:43 185 million years before the dinosaurs’ demise, did an asteroid nearly end life on Earth?, 4:34–4:39 A Aligned aurorae, 8:27 All about the Veil Nebula, 6:56–6:61 Amateur astronomy’s greatest generation, 8:68–8:71 Amateurs see fireballs from U.S. satellite kill, 7:24 Another Earth, 6:13 Another super-Earth discovered, 9:21 Antares gang, The, 7:18 Antimatter traced, 5:23 Are big-planet systems uncommon?, 10:23 Are super-sized Earths the new frontier?, 11:26–11:31 Are these space rocks from Mercury?, 11:32–11:37 Are we done yet?, 4:14 Are we looking for life in the right places?, 7:28–7:33 Ask the aliens, 3:12 Asteroid sleuths find the dino killer, 1:20 Astro-humiliation, 10:14 Astroimaging over ancient Greece, 12:64–12:69 Astronaut rescue rocket revs up, 11:22 Astronomers spy a giant particle accelerator in the sky, 5:21 Astronomers unearth a star’s death secrets, 10:18 Astronomers witness alien star flip-out, 6:27 Astronomy magazine’s first 35 years, 8:supplement Astronomy’s guide to Go-to telescopes, 10:supplement Auroral storm trigger confirmed, 11:18 B Backstage at Astronomy, 8:76–8:82 Basking in the Sun, 5:16 Biggest planet’s 5 deepest mysteries, The, 1:38–1:43 Binary pulsar test affirms relativity, 10:21 Binocular Telescope snaps first image, 6:21 Black hole sets a record, 2:20 Black holes wind up galaxy arms, 9:19 Brightest starburst galaxy discovered, 12:23 C Calling all space probes, 10:64–10:65 Calling on Cassiopeia, 11:76 Canada to launch new asteroid hunter, 11:19 Canada’s handy robot, 1:24 Cannibal next door, The, 3:38 Capture images of our local star, 4:66–4:67 Cassini confirms Titan lakes, 12:27 Cassini scopes Saturn’s two-toned moon, 1:25 Cassini “tastes” Enceladus’ plumes, 7:26 Cepheus’ fall delights, 10:85 Choose the dome that’s right for you, 5:70–5:71 Clearing the air about seeing vs. -

And Ecclesiastical Cosmology
GSJ: VOLUME 6, ISSUE 3, MARCH 2018 101 GSJ: Volume 6, Issue 3, March 2018, Online: ISSN 2320-9186 www.globalscientificjournal.com DEMOLITION HUBBLE'S LAW, BIG BANG THE BASIS OF "MODERN" AND ECCLESIASTICAL COSMOLOGY Author: Weitter Duckss (Slavko Sedic) Zadar Croatia Pусскй Croatian „If two objects are represented by ball bearings and space-time by the stretching of a rubber sheet, the Doppler effect is caused by the rolling of ball bearings over the rubber sheet in order to achieve a particular motion. A cosmological red shift occurs when ball bearings get stuck on the sheet, which is stretched.“ Wikipedia OK, let's check that on our local group of galaxies (the table from my article „Where did the blue spectral shift inside the universe come from?“) galaxies, local groups Redshift km/s Blueshift km/s Sextans B (4.44 ± 0.23 Mly) 300 ± 0 Sextans A 324 ± 2 NGC 3109 403 ± 1 Tucana Dwarf 130 ± ? Leo I 285 ± 2 NGC 6822 -57 ± 2 Andromeda Galaxy -301 ± 1 Leo II (about 690,000 ly) 79 ± 1 Phoenix Dwarf 60 ± 30 SagDIG -79 ± 1 Aquarius Dwarf -141 ± 2 Wolf–Lundmark–Melotte -122 ± 2 Pisces Dwarf -287 ± 0 Antlia Dwarf 362 ± 0 Leo A 0.000067 (z) Pegasus Dwarf Spheroidal -354 ± 3 IC 10 -348 ± 1 NGC 185 -202 ± 3 Canes Venatici I ~ 31 GSJ© 2018 www.globalscientificjournal.com GSJ: VOLUME 6, ISSUE 3, MARCH 2018 102 Andromeda III -351 ± 9 Andromeda II -188 ± 3 Triangulum Galaxy -179 ± 3 Messier 110 -241 ± 3 NGC 147 (2.53 ± 0.11 Mly) -193 ± 3 Small Magellanic Cloud 0.000527 Large Magellanic Cloud - - M32 -200 ± 6 NGC 205 -241 ± 3 IC 1613 -234 ± 1 Carina Dwarf 230 ± 60 Sextans Dwarf 224 ± 2 Ursa Minor Dwarf (200 ± 30 kly) -247 ± 1 Draco Dwarf -292 ± 21 Cassiopeia Dwarf -307 ± 2 Ursa Major II Dwarf - 116 Leo IV 130 Leo V ( 585 kly) 173 Leo T -60 Bootes II -120 Pegasus Dwarf -183 ± 0 Sculptor Dwarf 110 ± 1 Etc. -
Space Scoop Is Based on a Press Release from Noirlab
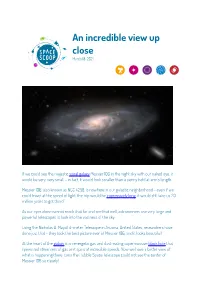
An incredible view up close March 18, 2021 If we could see the majestic spiral galaxy Messier 106 in the night sky with our naked eye, it would be very, very small - in fact, it would look smaller than a penny held at arm’s length. Messier 106, also known as NGC 4258, is nowhere in our galactic neighborhood - even if we could travel at the speed of light, the trip would be impressively long: it would still take us 20 million years to get there! As our eyes alone cannot reach that far and see that well, astronomers use very large and powerful telescopes to look into the vastness of the sky. Using the Nicholas U. Mayall 4-meter Telescope in Arizona, United States, researchers have done just that - they took the best picture ever of Messier 106, and it looks beautiful! At the heart of the galaxy is an energetic gas and dust-eating supermassive black hole that spews red streamers of gas as it spins at incredible speeds. Now we have a better view of what is happening there. Even the Hubble Space Telescope could not see the center of Messier 106 so clearly! Standard candles The spiral galaxy Messier 106 is especially important because it contains Cepheid variables - one of the objects that are used as “cosmic yardsticks” to measure the scale of the Universe. Astronomers call these objects “standard candles,” since their luminosity is well known. Scientists then compare the real brightness of these standard candles with how bright these objects appear to be for us here on Earth. -

Multi-Messenger Observations of a Binary Neutron Star Merger
DRAFT VERSION OCTOBER 6, 2017 Typeset using LATEX twocolumn style in AASTeX61 MULTI-MESSENGER OBSERVATIONS OF A BINARY NEUTRON STAR MERGER LIGO SCIENTIFIC COLLABORATION,VIRGO COLLABORATION AND PARTNER ASTRONOMY GROUPS (Dated: October 6, 2017) ABSTRACT On August 17, 2017 a binary neutron star coalescence candidate (later designated GW170817) with merger time 12:41:04 UTC was observed through gravitational waves by the Advanced LIGO and Advanced Virgo detectors. The Fermi Gamma-ray Burst Monitor independently detected a gamma-ray burst (GRB170817A) with a time-delay of 1.7swith respect to the merger ⇠ time. From the gravitational-wave signal, the source was initially localized to a sky region of 31 deg2 at a luminosity distance +8 of 40 8 Mpc and with component masses consistent with neutron stars. The component masses were later measured to be in the range− 0.86 to 2.26 M . An extensive observing campaign was launched across the electromagnetic spectrum leading to the discovery of a bright optical transient (SSS17a, now with the IAU identification of AT2017gfo) in NGC 4993 (at 40 Mpc) less ⇠ than 11 hours after the merger by the One-Meter, Two Hemisphere (1M2H) team using the 1-m Swope Telescope. The optical transient was independently detected by multiple teams within an hour. Subsequent observations targeted the object and its environment. Early ultraviolet observations revealed a blue transient that faded within 48 hours. Optical and infrared observations showed a redward evolution over 10 days. Following early non-detections, X-ray and radio emission were discovered at the ⇠ transient’s position 9 and 16 days, respectively, after the merger. -

The Messier Catalog
The Messier Catalog Messier 1 Messier 2 Messier 3 Messier 4 Messier 5 Crab Nebula globular cluster globular cluster globular cluster globular cluster Messier 6 Messier 7 Messier 8 Messier 9 Messier 10 open cluster open cluster Lagoon Nebula globular cluster globular cluster Butterfly Cluster Ptolemy's Cluster Messier 11 Messier 12 Messier 13 Messier 14 Messier 15 Wild Duck Cluster globular cluster Hercules glob luster globular cluster globular cluster Messier 16 Messier 17 Messier 18 Messier 19 Messier 20 Eagle Nebula The Omega, Swan, open cluster globular cluster Trifid Nebula or Horseshoe Nebula Messier 21 Messier 22 Messier 23 Messier 24 Messier 25 open cluster globular cluster open cluster Milky Way Patch open cluster Messier 26 Messier 27 Messier 28 Messier 29 Messier 30 open cluster Dumbbell Nebula globular cluster open cluster globular cluster Messier 31 Messier 32 Messier 33 Messier 34 Messier 35 Andromeda dwarf Andromeda Galaxy Triangulum Galaxy open cluster open cluster elliptical galaxy Messier 36 Messier 37 Messier 38 Messier 39 Messier 40 open cluster open cluster open cluster open cluster double star Winecke 4 Messier 41 Messier 42/43 Messier 44 Messier 45 Messier 46 open cluster Orion Nebula Praesepe Pleiades open cluster Beehive Cluster Suburu Messier 47 Messier 48 Messier 49 Messier 50 Messier 51 open cluster open cluster elliptical galaxy open cluster Whirlpool Galaxy Messier 52 Messier 53 Messier 54 Messier 55 Messier 56 open cluster globular cluster globular cluster globular cluster globular cluster Messier 57 Messier -

SALT ANNUAL REPORT 2017 BEGINNING of a NEW ERA Multi-Messenger Events: Combining Gravitational Wave and Electromagnetic Astronomy
SALT ANNUAL REPORT 2017 BEGINNING OF A NEW ERA Multi-messenger events: combining gravitational wave and electromagnetic astronomy A NEW KIND OF SUPERSTAR: KILONOVAE − VIOLENT MERGERS OF NEUTRON STAR BINARIES On 17 August 2017 the LIGO and Virgo gravitational wave observatories discovered their first candidate for the merger of a neutron star binary. The ensuing explosion, a kilonova, which was observed in the lenticular galaxy NGC 4993, is the first detected electromagnetic counterpart of a gravitational wave event. One of the earliest optical spectra of the kilonova, AT However, a simple blackbody is not sufficient to explain the 2017gfo, was taken using RSS on SALT. This spectrum was data: another source of luminosity or opacity is necessary. featured in the multi-messenger summary paper by the Predictions from simulations of kilonovae qualitatively full team of 3677 collaborators. Combining this spectrum match the observed spectroscopic evolution after two with another SALT spectrum, as well as spectra from the days past the merger, but underpredict the blue flux in Las Cumbres Observatory network and Gemini–South, the earliest spectrum from SALT. From the best-fit models, Curtis McCully from the Las Cumbres Observatory and the team infers that AT 2017gfo had an ejecta mass of his colleagues were able to follow the full evolution of 0.03 solar masses, high ejecta velocities of 0.3c, and a the kilonova. The spectra evolved very rapidly, from low mass fraction ~0.0001 of high-opacity lanthanides blue (~6400K) to red (~3500K) over the three days they and actinides. One possible explanation for the early observed. -

X-Ray Luminosities for a Magnitude-Limited Sample of Early-Type Galaxies from the ROSAT All-Sky Survey
Mon. Not. R. Astron. Soc. 302, 209±221 (1999) X-ray luminosities for a magnitude-limited sample of early-type galaxies from the ROSAT All-Sky Survey J. Beuing,1* S. DoÈbereiner,2 H. BoÈhringer2 and R. Bender1 1UniversitaÈts-Sternwarte MuÈnchen, Scheinerstrasse 1, D-81679 MuÈnchen, Germany 2Max-Planck-Institut fuÈr Extraterrestrische Physik, D-85740 Garching bei MuÈnchen, Germany Accepted 1998 August 3. Received 1998 June 1; in original form 1997 December 30 Downloaded from https://academic.oup.com/mnras/article/302/2/209/968033 by guest on 30 September 2021 ABSTRACT For a magnitude-limited optical sample (BT # 13:5 mag) of early-type galaxies, we have derived X-ray luminosities from the ROSATAll-Sky Survey. The results are 101 detections and 192 useful upper limits in the range from 1036 to 1044 erg s1. For most of the galaxies no X-ray data have been available until now. On the basis of this sample with its full sky coverage, we ®nd no galaxy with an unusually low ¯ux from discrete emitters. Below log LB < 9:2L( the X-ray emission is compatible with being entirely due to discrete sources. Above log LB < 11:2L( no galaxy with only discrete emission is found. We further con®rm earlier ®ndings that Lx is strongly correlated with LB. Over the entire data range the slope is found to be 2:23 60:12. We also ®nd a luminosity dependence of this correlation. Below 1 log Lx 40:5 erg s it is consistent with a slope of 1, as expected from discrete emission. -

7.5 X 11.5.Threelines.P65
Cambridge University Press 978-0-521-19267-5 - Observing and Cataloguing Nebulae and Star Clusters: From Herschel to Dreyer’s New General Catalogue Wolfgang Steinicke Index More information Name index The dates of birth and death, if available, for all 545 people (astronomers, telescope makers etc.) listed here are given. The data are mainly taken from the standard work Biographischer Index der Astronomie (Dick, Brüggenthies 2005). Some information has been added by the author (this especially concerns living twentieth-century astronomers). Members of the families of Dreyer, Lord Rosse and other astronomers (as mentioned in the text) are not listed. For obituaries see the references; compare also the compilations presented by Newcomb–Engelmann (Kempf 1911), Mädler (1873), Bode (1813) and Rudolf Wolf (1890). Markings: bold = portrait; underline = short biography. Abbe, Cleveland (1838–1916), 222–23, As-Sufi, Abd-al-Rahman (903–986), 164, 183, 229, 256, 271, 295, 338–42, 466 15–16, 167, 441–42, 446, 449–50, 455, 344, 346, 348, 360, 364, 367, 369, 393, Abell, George Ogden (1927–1983), 47, 475, 516 395, 395, 396–404, 406, 410, 415, 248 Austin, Edward P. (1843–1906), 6, 82, 423–24, 436, 441, 446, 448, 450, 455, Abbott, Francis Preserved (1799–1883), 335, 337, 446, 450 458–59, 461–63, 470, 477, 481, 483, 517–19 Auwers, Georg Friedrich Julius Arthur v. 505–11, 513–14, 517, 520, 526, 533, Abney, William (1843–1920), 360 (1838–1915), 7, 10, 12, 14–15, 26–27, 540–42, 548–61 Adams, John Couch (1819–1892), 122, 47, 50–51, 61, 65, 68–69, 88, 92–93, -

The 2Mass Redshift Survey—Description and Data Release
The Astrophysical Journal Supplement Series, 199:26 (22pp), 2012 April doi:10.1088/0067-0049/199/2/26 C 2012. The American Astronomical Society. All rights reserved. Printed in the U.S.A. THE 2MASS REDSHIFT SURVEY—DESCRIPTION AND DATA RELEASE John P. Huchra1,15, Lucas M. Macri2, Karen L. Masters3,4, Thomas H. Jarrett5, Perry Berlind1, Michael Calkins1, Aidan C. Crook6, Roc Cutri4, Pirin Erdogduˇ 7, Emilio Falco1, Teddy George8, Conrad M. Hutcheson9, Ofer Lahav7, Jeff Mader10, Jessica D. Mink1, Nathalie Martimbeau11, Stephen Schneider12, Michael Skrutskie13, Susan Tokarz1, and Michael Westover14 1 Harvard-Smithsonian Center for Astrophysics, 60 Garden Street, Cambridge, MA 02138, USA 2 George P. and Cynthia Woods Mitchell Institute for Fundamental Physics and Astronomy, Department of Physics and Astronomy, Texas A&M University, 4242 TAMU, College Station, TX 77843, USA; [email protected] 3 Institute for Cosmology and Gravitation, University of Portsmouth, Dennis Sciama Building, Burnaby Road, Portsmouth, PO1 3FX, UK; [email protected] 4 SEPNet (South East Physics Network), UK 5 Infrared Processing and Analysis Center, California Institute of Technology, 770 S Wilson Ave., Pasadena, CA 91125, USA 6 Microsoft Corp., 1 Microsoft Way, Redmond, WA 98052, USA 7 Department of Physics and Astronomy, University College London, London WC1E 6BT, UK 8 Canada–France–Hawaii Telescope, 65-1238 Mamalahoa Hwy, Kamuela, HI 96743, USA 9 Kavli Institute for Particle Astrophysics and Cosmology, Stanford University, Stanford, CA 94309, USA 10 Keck Observatory, -

Astronomy and Astrophysics Books in Print, and to Choose Among Them Is a Difficult Task
APPENDIX ONE Degeneracy Degeneracy is a very complex topic but a very important one, especially when discussing the end stages of a star’s life. It is, however, a topic that sends quivers of apprehension down the back of most people. It has to do with quantum mechanics, and that in itself is usually enough for most people to move on, and not learn about it. That said, it is actually quite easy to understand, providing that the information given is basic and not peppered throughout with mathematics. This is the approach I shall take. In most stars, the gas of which they are made up will behave like an ideal gas, that is, one that has a simple relationship among its temperature, pressure, and density. To be specific, the pressure exerted by a gas is directly proportional to its temperature and density. We are all familiar with this. If a gas is compressed, it heats up; likewise, if it expands, it cools down. This also happens inside a star. As the temperature rises, the core regions expand and cool, and so it can be thought of as a safety valve. However, in order for certain reactions to take place inside a star, the core is compressed to very high limits, which allows very high temperatures to be achieved. These high temperatures are necessary in order for, say, helium nuclear reactions to take place. At such high temperatures, the atoms are ionized so that it becomes a soup of atomic nuclei and electrons. Inside stars, especially those whose density is approaching very high values, say, a white dwarf star or the core of a red giant, the electrons that make up the central regions of the star will resist any further compression and themselves set up a powerful pressure.1 This is termed degeneracy, so that in a low-mass red 191 192 Astrophysics is Easy giant star, for instance, the electrons are degenerate, and the core is supported by an electron-degenerate pressure.