Habitability of Exoplanetary Systems
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
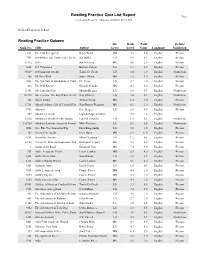
Reading Practice Quiz List Report Page 1 Accelerated Reader®: Thursday, 05/20/10, 09:41 AM
Reading Practice Quiz List Report Page 1 Accelerated Reader®: Thursday, 05/20/10, 09:41 AM Holden Elementary School Reading Practice Quizzes Int. Book Point Fiction/ Quiz No. Title Author Level Level Value Language Nonfiction 661 The 18th Emergency Betsy Byars MG 4.1 3.0 English Fiction 7351 20,000 Baseball Cards Under the Sea Jon Buller LG 2.6 0.5 English Fiction 11592 2095 Jon Scieszka MG 4.8 2.0 English Fiction 6201 213 Valentines Barbara Cohen LG 3.1 2.0 English Fiction 30629 26 Fairmount Avenue Tomie De Paola LG 4.4 1.0 English Nonfiction 166 4B Goes Wild Jamie Gilson MG 5.2 5.0 English Fiction 9001 The 500 Hats of Bartholomew CubbinsDr. Seuss LG 3.9 1.0 English Fiction 413 The 89th Kitten Eleanor Nilsson MG 4.3 2.0 English Fiction 11151 Abe Lincoln's Hat Martha Brenner LG 2.6 0.5 English Nonfiction 61248 Abe Lincoln: The Boy Who Loved BooksKay Winters LG 3.6 0.5 English Nonfiction 101 Abel's Island William Steig MG 6.2 3.0 English Fiction 13701 Abigail Adams: Girl of Colonial Days Jean Brown Wagoner MG 4.2 3.0 English Nonfiction 9751 Abiyoyo Pete Seeger LG 2.8 0.5 English Fiction 907 Abraham Lincoln Ingri & Edgar d'Aulaire 4.0 1.0 English 31812 Abraham Lincoln (Pebble Books) Lola M. Schaefer LG 1.5 0.5 English Nonfiction 102785 Abraham Lincoln: Sixteenth President Mike Venezia LG 5.9 0.5 English Nonfiction 6001 Ace: The Very Important Pig Dick King-Smith LG 5.0 3.0 English Fiction 102 Across Five Aprils Irene Hunt MG 8.9 11.0 English Fiction 7201 Across the Stream Mirra Ginsburg LG 1.2 0.5 English Fiction 17602 Across the Wide and Lonesome Prairie:Kristiana The Oregon Gregory Trail Diary.. -

Download This Issue
WINTER 2018-19 COLUMBIA MAGAZINE COLUMBIA COLUMBIA MAGAZINE WINTER 2018-19 4.18_Cover_F.indd 1 11/14/18 12:17 PM Check in with Columbia everyevery dayday Visit the brand-new magazine.columbia.edu to fi nd the latest research, compelling stories, alumni news, and more @ColumbiaMag @columbiamag @columbiamagazine 4.18_AD_Columbia-Magazine_F.indd 1 11/14/18 4:28 PM WINTER 2018-19 PAGE 30 CONTENTS FEATURES 12 UPPER WEST SIDE STORIES The little-known tale of two Columbia teachers and the classes that inspired J.D. Salinger, Truman Capote, Carson McCullers, and a generation of American writers By Paul Hond 18 BULLET POINTS Anger. Fear. Frustration. Hope? A year in the life of a reporter on the front lines of America’s gun-violence epidemic. By Jennifer Mascia ’07JRN 24 CORE CURRICULUM What deep-sea sediment can tell us about climate change By David J. Craig and Jackie Roche 30 LEAP OF FAITH Dancer Michael Novak ’09GS has been cast in the role of a lifetime — Paul Taylor’s successor By Rebecca Shapiro 36 THE SCIENCE OF HEALTHY AGING A Q&A with Linda P. Fried on the secrets to living a longer, healthier, and happier life By David J. Craig COVER ILLUSTRATION BY JASU HU CREATIVE / LASPATA DECARO / LASPATA CREATIVE COLUMBIA WINTER 2018-19 1 4.18_Contents.indd 1 11/15/18 1:06 PM COLUMBIA CONTENTS MAGAZINE DEPARTMENTS Executive Vice President, 3 University Development & Alumni Relations FEEDBACK Amelia Alverson Deputy Vice President for Strategic Communications 6 Jerry Kisslinger ’79CC, ’82GSAS COLLEGE WALK They Shall Be Rereleased \ The Short List \ The Forum Sets Sail \ Through the Future, Editor in Chief Sally Lee Darkly \ In Memoriam LBB Art Director 40 Len Small EXPLORATIONS Managing Editor New smart helmet could spot concussions in Rebecca Shapiro PAGE real time \ What fi sh can teach us about our 36 Senior Editors powers of perception \ New fl ight routes save David J. -

Street Name Street Suffix Direction AARON AL ABBEY HILL ABBIE PL
Street Name Street Suffix Direction AARON AL ABBEY HILL ABBIE PL ABBINGTON RIDGE ABBOTT LN ABBOTT ST ABBOTTSFORD AVE ABBOTTSFORD ST ABBY CT ABELIA CT ABILENE TL ABINGTON AVE ACADEMY AVE ACCESS PL ACKLEY RD ACOMB AVE ACORN DR ACRE DR ACREVIEW DR ACREWOOD DR ACTON CT ADA ST ADAIR CT ADAMS AVE ADAMS RD ADAMS ST ADAMS CREEK DR ADAMS CROSSING ADAMS RIDGE DR ADDICE WY ADDINGHAM PL ADDISON ST ADDYSTON ST ADELAIDE ST ADELLE WALK ADELPHI ST ADENA TL ADMIRAL CT ADNORED CT ADONY AVE ADVANCE AVE ADVENTURE LN ADWOOD DR AFFINITY DR AFFINITY PL AFFIRMED DR AFTON AVE AGNES ST AHRENS ST AHWENASA LN AIKENSIDE AVE AINSWORTH CT AIRPORT RD AIRY CT AIRYCREST LN AIRYMEADOWS DR AIRYMONT CT AKOCHIA AVE AKRON AVE ALABAMA AVE ALAMO AVE ALAMOSA DR ALASKA AVE ALASKA CT ALBA CT ALBANO ST ALBANY TE ALBERLY LN ALBERT PL ALBERT ST ALBERT SABIN WY ALBERTS CT ALBION AVE ALBION LN ALBION PL ALBRIGHT DR ALCLIFF LN ALCOR TE ALCOTT LN ALDBOUGH CT ALDEN AL ALDER LN ALDERMONT CT ALDINE DR ALDON LN ALDRICH AVE ALEX AVE ALEXANDER ST ALEXANDRAS OAK CT ALEXANDRAS RIDGE DR ALEXIS RD ALFRED ST ALGIERS DR ALGONA PL ALGONQUIN DR ALGUS LN ALHAMBRA CT ALICE ST ALICEMONT AVE ALJOY CT ALLAIRE AVE ALLEGHENY DR ALLEGRO CT ALLEN AVE ALLENCREST CT ALLENDALE DR ALLENDORF DR ALLENFORD CT ALLENHAM ST ALLENHURST BV E ALLENHURST BV W ALLENHURST CLOSE CT ALLENWOOD CT ALLET AVE ALLIANCE RD ALLISON AVE ALLISON ST ALLSTON ST ALLVIEW CR ALLVIEW CT ALMA ST ALMAHURST CT ALMESTER DR ALMS PL ALNETTA DR ALOMAR DR ALPHA ST ALPHONSE LN ALPINE AVE ALPINE PL ALPINE TE ALTA AVE ALTA VISTA AVE ALTADENA AVE ALTAVIEW -

Faculty Creative Works 2016
Faculty Creative Works 2016 Jody Bailey, Editor Michelle Reed, Editor Mavs Open Press 2017 Faculty Creative Works 2016 This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License. To view a copy of this license, visit: http://creativecommons.org/licenses/by-nc/4.0/ or send a letter to: Creative Commons PO Box 1866 Mountain View, CA 94042 USA Book design by Kyle Pinkos Published by: Mavs Open Press University of Texas at Arlington Libraries 702 Planetarium Place Arlington, TX 76019 Faculty Creative Works 2016 Introduction he Libraries of the University of Texas at Arlington are pleased to host the ninth annual UTA Celebration of Faculty Creative Works. This event showcases the art, books, juried exhibits, music, Tmedia, patents, and journal contributions of UTA faculty in 2016. The Libraries initiated this event to shine a spotlight on the impressive depth and breadth of scholarship and creativity produced by UTA faculty. These scholars are achieving unprecedented excellence in research, teaching, and community engagement. 1 Each year the number of scholars we honor grows. This year we have a 25% increase in faculty scholarly citations and have grown to represent over 400 faculty. We congratulate the colleagues represented in these pages and on the Faculty Creative Works website at library.uta.edu/fcw. Their work epitomizes the high standards of excellence and the growth of research activity at UTA. Rebecca Bichel UTA Libraries Dean Faculty Creative Works 2016 Contents Introduction 1 College of Architecture, Planning and Public Affairs 3 College of Business 6 College of Education 14 2 College of Engineering 19 College of Liberal Arts 52 College of Nursing and Health Innovation 77 College of Science 83 School of Social Work 115 Libraries 123 Acknowledgments 128 Index 129 Faculty Creative Works 2016 College of Architecture, Planning and Public Affairs Nan Ellin, Dean Holliday, Kate, et al. -

Uranus' Moon Titania 6 July 2015, by Matt Williams
Uranus' moon Titania 6 July 2015, by Matt Williams than Herschel would observe them. In addition, Titania would be referred to as "the first satellite of Uranus" for many years – or by the designation Uranus I, which was given to it by William Lassell in 1848. By 1851, Lassell began to number all four known satellites in order of their distance from the planet by Roman numerals, at which point Titania's designation became Uranus III. By 1852, Herschel's son John, and at the behest of Lassell himself, suggested the moon's name be changed to Titania, the Queen of the Fairies in A Midsummer Night's Dream. This was consistent with all of Uranus' satellites, which were given names from the works of William Shakespeare and Alexander Pope. Voyager 2 image of Titania, Uranus’ largest moon. Credit: NASA Size, Mass and Orbit: With a diameter of 1,578 kilometers, a surface area of 7,820,000 km² and a mass of 3.527±0.09 × Like all of the Solar Systems' gas giants, Uranus 1021 kg, Titania is the largest of Uranus' moons has an extensive system of moons. In fact, and the eighth largest moon in the Solar System. At astronomers can now account for 27 moons in a distance of about 436,000 km (271,000 mi), orbit around Uranus. Of these, none are greater in Titania is also the second farthest from the planet size, mass, or surface area than Titania. One of of the five major moons. the first moon's to be discovered around Uranus, this heavily cratered and scarred moon was Titania's moon also has a small eccentricity and is appropriately named after the fictional Queen of inclined very little relative to the equator of Uranus. -

Uranus System: 27 Satellites, Rings
Uranus System: 27 Satellites, Rings 1 27 Uranian Satellites Distance Radius Mass Satellite (000 km) (km) (kg) Discoverer Date --------- -------- ------ ------- ---------- ----- Cordelia 50 13 ? Voyager 2 1986 Ophelia 54 16 ? Voyager 2 1986 Bianca 59 22 ? Voyager 2 1986 Cressida 62 33 ? Voyager 2 1986 Desdemona 63 29 ? Voyager 2 1986 Juliet 64 42 ? Voyager 2 1986 Portia 66 55 ? Voyager 2 1986 Rosalind 70 27 ? Voyager 2 1986 Cupid (2003U2) 75 6 ? Showalter 2003 Belinda 75 34 ? Voyager 2 1986 Perdita 76 40 ? Voyager 2 1986 Puck 86 77 ? Voyager 2 1985 Mab (2003U1) 98 8 ? Showalter 2003 Miranda 130 236 6.30e19 Kuiper 1948 Ariel 191 579 1.27e21 Lassell 1851 Umbriel 266 585 1.27e21 Lassell 1851 Titania 436 789 3.49e21 Herschel 1787 Oberon 583 761 3.03e21 Herschel 1787 Francisco 4281 6 ? Holman 2003 Caliban 7169 40 ? Gladman 1997 Stephano 7948 15 ? Gladman 1999 Trinculo 8578 5 ? Holman 2001 Sycorax 12213 80 ? Nicholson 1997 Margaret 14689 6 ? Sheppard 2003 Prospero 16568 20 ? Holman 1999 Setebos 17681 20 ? Kavelaars 1999 Ferdinand 21000 6 ? Sheppard 2003 2 Uranian Satellites Oberon Titania Umbriel Miranda Ariel Puck 3 Uranian and Saturnian Satellites Distance Radius Mass Satellite (000 km) (km) (kg) Discoverer Date Epimetheus 151 57 5.60e17 Walker 1980 Puck 86 77 ? Voyager 2 1985 Janus 151 89 2.01e18 Dollfus 1966 Phoebe 12952 110 4.00e18 Pickering 1898 Hyperion 1481 143 1.77e19 Bond 1848 Mimas 186 196 3.80e19 Herschel 1789 Miranda 130 236 6.30e19 Kuiper 1948 Enceladus 238 260 8.40e19 Herschel 1789 Tethys 295 530 7.55e20 Cassini 1684 Dione 377 560 1.05e21 Cassini 1684 Ariel 191 579 1.27e21 Lassell 1851 Umbriel 266 585 1.27e21 Lassell 1851 Iapetus 3561 730 1.88e21 Cassini 1671 Oberon 583 761 3.03e21 Herschel 1787 Rhea 527 765 2.49e21 Cassini 1672 Titania 436 789 3.49e21 Herschel 1787 Titan 1222 2575 1.35e23 Huygens 1655 4 Uranian Satellites Distance Radius Mass Density Inc. -
SHAKESPEARE's FEMALE Icons
The start ow SHAKESPEARE's FEMALE IcoNs Volume XXXI 2012 Vol. XXXI Digital Facsimile The Upstart Crow: A Shakespeare journal, Volume XXXI, 2012 is published by Clemson Universicy Digital Press. © 2013 Clemson Univcrsicy ISSN: 0886-2168 ~ EDITOR ·~ \ Elizabeth Rivlin CLEMSON UNIVERSITY DIGITAL PRESS ASSOCIATE EDITORS Ray Barfield, Wayne Chapman, Jonathan Field, Martin Jacobi, Michael LeMahieu, Chantelle MacPhee, Brian McGrath, Lee Morrissey, and Will Stockton BOOK REVIEW EDITOR Will Stockton, Clemson University ADVISORY BOARD James Berg, Pam Brown, Patricia Cahill, Ann C. Christensen, Katherine Conway, Herbert Coursen, Mary Agnes Edsall, John R. Ford, Walter Haden, Chris Hassel, Maurice Hunt, Natasha Korda, Paul Kottman, Richard Levin, Jeremy Lopez, Bindu Malieckal, John McDaniel, Ian Frederick Moulton, Peter Pauls, Kaara Peterson, Jeanne Roberts, and Jyotsna Singh BUSINESS MANAGER Kristin Sindorf ACCOUNTING FISCAL ANALYST Beverly Pressley EDITORIAL ASSISTANTS Charis Chapman and Jared Jamison EDITORIAL CORRESPONDENCE Editor, 1he Upstart Crow, Department of English, Clemson University, Strode Tower, Box 340523, Clemson, SC 29634-0523. Tel. (864) 656-3151. Fax (864) 656-1345. SUBSCRIPTION RATES Please note: after Volume XXXI, "'ubscription will no longer be available although copies of most volumes may be purchased from the online store to which visitors to our website will be directed. PDF facsimiles of all volumes, in the ncar future, wiU be available free for viewing on an open-access basis. Queries on existing subscriptions should be directed to The Business Manager at the same address as given above. Meanwhile, rates for the present (and last) volume of 1he Upstart Crow are as follows: 1-year subscription for individuals (Vol. XXXI): $17 1-year subscription for institutions (Vol. -

Appendix a Luna and Telescopes
Appendix A Luna and Telescopes Exploring Luna’s surface is one of the easiest things to do in this book. You have a few options when you do this. It has the advan- tage of being the only moon visible to the naked eyes. (You might be able to just see the Galilean moons, but you would hardly be able to do anything beyond just see them.) So the next step is to consider an instrument. Be aware, this is not a general purpose guide. If you want one, look at the local library or bookseller for a copy of “NightWatch” as the book is excellent, has a sturdy plastic spiral for easy hands- free use and will serve you in more ways than just binoculars for many years to come. That being said all my recommendations in this chapter are for viewing ONLY OUR MOON. Most other moons will be pinpricks, so if you can see them at all you did the best you could. If you also wish to view nebula, galaxies, birds, be rude to your neighbors, and so forth, do your homework. Binoculars The first option is to go with binoculars. These come in a variety of sizes, which is listed as two numbers. The first is magnification and the second is aperture size (in mm). Common sizes include 7 × 35, 7 × 42, 8 × 40, 9 × 50 or even 10 × 50. For dim object you will want the bigger sizes, but the moon is not a dim object. Even a 7 × 35 will produce some pretty spectacular views. -

2019 Publication Year 2021-02-19T14:37:09Z Acceptance
Publication Year 2019 Acceptance in OA@INAF 2021-02-19T14:37:09Z Title Uranus and Neptune Authors FILACCHIONE, GIANRICO; CIARNIELLO, Mauro DOI 10.1016/B978-0-12-409548-9.11942-6 Handle http://hdl.handle.net/20.500.12386/30481 Uranus and Neptune Gianrico Filacchione and Mauro Ciarniello, Institute for Space Astrophysics and Planetology, Rome, Italy © 2019 Elsevier Inc. All rights reserved. Introduction 1 Uranus 1 Neptune 2 Satellites 3 Rings 6 Further Reading 8 Glossary Diapir Is an upwelling of material, or intrusion, moving into overlying surface. They follow Rayleigh-Taylor instability patterns (mushroom or dikes shapes) depending on the tectonic environment and density contrast between the intrusion material and the surface. Geometric Albedo Brightness of a planet or satellite measured at null solar phase angle ratioed to that of a lambertian (ideal fully reflective) surface with the same dimension. For surfaces made up of small water ice grains the geometric albedo can be >1, meaning that the surface is more efficient than an ideal lambertian surface in scattering back the received light. Hydrostatic equilibrium A body reaches hydrostatic equilibrium when it assumes spherical (or ellipsoid) shape under its own gravity. This condition happens when gravity is balanced by pressure. About 30 objects in the Solar System are known to be in hydrostatic equilibrium and this criterion is currently used to distinguish dwarf planets from small bodies. Leading hemisphere The hemisphere of a satellite that faces into the direction of motion. This applies to satellites in synchronous orbits, thus always keeping the same face towards the planet. Optical depth This is a measure of the transparency of a ring system. -

6-24 PAC Plaza Pavers Database
Brick Area A Assigned # Column Row Full Name Key Word 10,071 1 1 LEROY AND BONNIE LARSON & FAMILY 1993 LARSON 10,072 1 2 JIM & JANE JOHNSON JUNE 10, 1961 JOHNSON 10,073 1 3 CHARLES & LEONA STROM STROM 10,074 1 4 THE ELLINGWOODS SCOTT‐TIM‐TYLER ELLINGWOOD 10,075 1 5 JEFF & TERRI MATTHIS MATTHIS 10,076 1 6 ART & ROSALIE RORAFF RORAFF 10,077 1 7 LOREN DODDS MILLE KIEVEN DODDS 10,078 1 8 JUANITA & GORDON BORT BORT 10,079 1 9 JOAN MARIANNA LAVAGETTO ANDERSON ANDERSON 10,080 1 10 CLARK MIS MELODY & NOVA SMITH FAMILY FAMILY 10,081 1 11 WE LOVE MYRA E HALLS SHE'S OUR GRAMS BEAR HALLS 10,082 1 12 KENNETH SUSAN BRANDON AMANDA HATCH HATCH 10,083 1 13 LEGALIZED GAMBOLING CHILKOOT CHARLIES CHILKOOT 10,084 1 14 THE HUNSUCKS 93 BILL PAM MEG TIA BABY HUNSUCKS 10,085 1 15 THE KEIFER FAMILY XMAS 92 LOVE KRISTEN KEIFER 10,086 1 16 SHANNON KATHY SEAN JENNI JIM STEPH EGAN EGAN 10,087 1 17 SCOTT ALAN IRWIN IRWIN 10,088 1 18 MEASURE PEOPLE BY DEPTH OF THEIR SOUL PEOPLE 10,089 1 19 SING GLORY TO GOD PS66 BROTHERS INDEED BROTHERS 10,090 1 20 VALERIE JANARD 1992 JANARD 10,091 1 21 EUNICE ASSELIN ASSELIN 10,092 1 22 WE 3 PIONEERS B L E... PIONEERS 10,093 1 23 CLAY & JANE DIAI DIAI 10,094 1 24 RIDE ON STEVE KEINER APRIL 8 1992 KEINER 10,095 1 25 MICHAEL R CENTER CENTER 10,096 1 26 BARBARA RHYNEER RHYNEER 10,097 1 27 JOSEPH WINSTON PREMO 03‐29‐91 PREMO 10,098 1 28 DAVID & ALEEN FISON 50TH ANNIV 7‐31‐93 FISON 10,099 1 29 TIFFANY AND GABBY CURTIS LOVE FROM MOM CURTIS 10,100 1 30 MILO BERNICE KIMBALL KIMBALL 10,101 2 1 SIENA EARLE & DAVID AUSMAN (SINCE 1950) AUSMAN -

Gertrude and Claudius: Reverse-Engineering Shakespeare Patrick Christopher Kavanagh BA, MA
Gertrude and Claudius: Reverse-engineering Shakespeare Patrick Christopher Kavanagh BA, MA English & Creative Writing Department Aberystwyth University Funded by Fergus Johnson Award Acknowledgements This thesis is dedicated to memory of my grandmother Margaret Fogarty — my favourite storyteller and a continued source of inspiration. ~ Firstly, I must thank my excellent supervisors, Prof. Tiffany Atkinson for her support and friendship throughout my academic career (and especially for her excellent poetry seminars during my Master’s); to Dr Gavin Goodwin for his dedication, diligence, sound advice and kindness; and to Prof. Matthew Francis for his encouragement throughout, which has meant more to me than I can ever express. And to all the staff (past and present) of my wonderful department, English and Creative Writing Aberystwyth Uni., where I have spent almost a fifth of my life (through B.A., M.A. and PhD); it has been a truly life-changing experience. Extra special thanks must go to the administrative staff, Julie, Sharon and Anka, who have been a friendly point of contact and source of knowledge throughout. And to Dr. Katherine Stansfield who seemed to see something of worth in my writing (her encouragement was so important!). I was lucky enough to teach three lots of 1st-year students over the course of my doctoral training and to them I owe a huge debt of gratitude: one learns so much from having to teach one’s subject to others. Also, heartfelt thanks to my superbly talented 2nd-year poetry cohort, thank you. To my other creative writing pupils at Plascrug School — I can only hope to one day write with the easy brilliance of a 5th-class kid. -
Appendix: Planetary Facts, Data and Tools
Appendix: Planetary Facts, Data and Tools Planetary Constants See Tables A1 and A2. © Springer International Publishing AG 2018 395 A.P. Rossi, S. van Gasselt (eds.), Planetary Geology, Springer Praxis Books, DOI 10.1007/978-3-319-65179-8 396 Appendix: Planetary Facts, Data and Tools Table A1 Bulk parameters for planets, dwarf planets and selected satellites Polar Equatorial Inverse Magnetic Atmospheric Mass radius radius flattening Density Gravity field pressure 24 3 2 Discovery Moons m [10 kg] rp [km] re [km] 1/f [–] [kg/m ] g [m/s ] B [T] p [bar] Planets Mercury prehistoric 0 0:330 2439:7 2439:7 – 5427 3:710 3.0107 1014 Venus prehistoric 0 4:868 6051:8 6051:8 – 5243 8:870 – 92 Earth prehistoric 1 5:972 6356:8 6378:1 298:253 5514 9:810 2.4105 1.014 Mars prehistoric 2 0:642 3376:2 3396:2 169:894 3933 3:710 – 0.006 Jupiter prehistoric 67 1898:190 66854:0 71492:0 15:41 1326 24:790 4.3104 > 1000 Saturn prehistoric 62 568:340 54364:0 60268:0 10:21 687 10:440 2.2105 > 1000 Uranus 1781 27 86:813 24973:0 25559:0 43:62 1271 8:870 2.3105 > 1000 Neptune 1846 14 102:413 24341:0 24764:0 58:54 1638 11:150 1.4105 > 1000 Dwarf m [1021 kg] planets (134340) 1930 5 13:030 1187:0 1187:0 – 1860 0:620 – 1109 Pluto (1) Ceres 1801 0 0:939 473:0 473:0 – 2161 0:280 – – (136199) 2005 1 16:600 1163:0 1163:0 – 2520 0:820 – – Eris (136472) 2005 1 < 4:400 715:0 715:0 20:00 1400 0:500 – 4–12109 Makemake 739:0 739:0 3200 (136108) 2004 2 4:010 620:0 620:0 – (min) 0:630 – – Haumea 2600 Appendix: Planetary Facts, Data and Tools 397 Satellites m [1021 kg] Earth’s moon