922 Structures and Magnetic Properties Of
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Coal Mine Methane Country Profiles, June 2015
Disclaimer The U.S. Environmental Protection Agency does not: a) Make any warranty or representation, expressed or implied, with respect to the accuracy, completeness, or usefulness of the information contained in this report, or that the use of any apparatus, method, or process disclosed in this report may not infringe upon privately owned rights; or b) Assume any liability with respect to the use of, or damages resulting from the use of, any information, apparatus, method, or process disclosed in this report. CMM Country Profiles CONTENTS Units of Conversions .............................................................................................................................................. i Executive Summary .............................................................................................................................................. ii Global Overview at a Glance ................................................................................................................................. ii Introduction ............................................................................................................................................................ 1 Purpose of the Report ............................................................................................................................................. 2 Organization of the Report ................................................................................................................................... 2 1 Argentina ...................................................................................................................................................... -

Fushun Four Page
FUSHUN MINING GROUP CO., LTD. L IAONING PROVINCE Opportunities for Investment in Coal Mine Methane Projects A major coal producer, the Fushun Mining Group Company, Ltd. has one producing underground mine and one open-pit mine. Total coal production in the mining area is about 6 million tonnes of coal annually. The underground mine, Laohutai, drains about 100 million cubic meters (more than 3.5 billion cubic feet) of methane annually, and methane production from surface boreholes has also begun. Significant opportunity exists for expanding recovery and utilization of methane from surface and underground boreholes. The Fushun Mining Group Company, Ltd. seeks investment for expanding the production of methane from surface boreholes and combining it with a portion of the methane recovered from the Laohutai mine to meet the energy needs of the nearby city of Shenyang. Fushun Mining Group seeks investment from China and abroad to for the proposed coal mine methane development project described in this brochure. OVERVIEW OF THE FUSHUN MINING GROUP COMPANY LTD. CHINA Fushun Mining Area LIAONING The Fushun Mining Group Company Ltd. (informally known as the Fushun Mining Group) is a large state-owned coal enterprise with 26 subsidiaries. Located in the city of Fushun in northeastern China’s Liaoning Province, it is about 45 km from Shenyang, the capital of the province, and 126 km from Anshan, a major iron and steel manufacturing center. Although the Fushun area has produced coal for more than 100 years, an estimated 800 million tonnes of recoverable reserves remain. The Fushun Mining Group has total assets of 4.7 billion yuan ($US 566 million). -

Coal Mine Methane Country Profiles, Chapter 7, June 2015
7 China 7.1 Summary of Coal Industry 7.1.1 ROLE OF COAL IN CHINA Coal accounts for 69 percent of total national energy consumption in China (EIA, 2014a). Ranking first in the world in production of coal, China exported 16.5 million tonnes (Mmt) of coal in 2011; a sharp decline from a peak of 108.8 Mmt in 2003 (EIA, 2014b). Historically, a net coal exporter, China became a net coal importer in 2009 for the first time in more than two decades (EIA, 2014a). Table 7-1 provides recoverable reserve and recent coal production data for China. Table 7-1. China’s Coal Reserves and Production Sub- Anthracite & Total bituminous & Global Rank Indicator Bituminous (million Lignite (# and %) (million tonnes) tonnes) (million tonnes) Estimated Proved Coal Reserves 62,200 52,300 114,500 3 (12.9%) (2011) Annual Coal Production (2012) 3,510.2 141.5 3,651.8 1 (46.3%) Note: Numbers may not add due to rounding Source: EIA (2014b) As shown in Figure 7-1, the following major coal basins are located in four regions of China (USEPA, 1996): . Sanjuang-Mulinghe, Songliao, Donhua-Fushun, and Hongyang-Hunjiang basins in the Northeast; . Taixing-Shandou, Qinshui, Daning, Ordos, Hedong, Yuxi, Xuhuai, and Huainan basins in the North; . Chuannon-Qianbei, Huayingshan-Yongrong, and Liapanshui basins in the South; and . Tarim, Qaidam, and Junggar basins in the Northwest. CMM Country Profiles 63 CHINA Figure 7-1. China’s Coal Fields Source: Liu (2006) 7.1.2 STAKEHOLDERS Table 7-2 identifies some of the key stakeholders for coal mine methane (CMM) project development in China. -

EMD Oil Shale Committee
EMD Oil Shale Committee EMD Oil Shale Committee Annual Report – 2015 Alan Burnham, Chair April 29, 2015 Vice-Chairs: Dr. Lauren Birgenheier (Vice-Chair – University) University of Utah Mr. Ronald C. Johnson (Vice-Chair – Government) U.S. Geological Survey Dr. Mariela Araujo (Vice-Chair – Industry) Shell International Exploration and Production Highlights Progress on oil shale continued in both the United States and around the world, but with a greater sense of urgency in countries with lesser quantities of conventional energy sources. New production capacity was brought on line in Estonia and China, and plans for production moved forward in Jordan. However, reductions and delays in development are starting to appear, particularly in the United States, due to the low price of crude oil. The current status is in flux, but it is too early to know whether we are seeing a repeat of the 1980s. In the U.S., the Utah Division of Water Quality issued a groundwater permit to Red Leaf Resources, which now has the go-ahead to establish a small-scale commercial production system based on the EcoShale process as a joint venture with Total. A challenge by environmental groups was settled by allowing access to groundwater monitoring data. However, that project is now delayed by a year or more, and the time will be used to accelerate design optimization. TomCo received temporary approval to establish a commercial operation using the EcoShale process 15 miles from the Red Leaf operation. Enefit is making progress getting permits for development of its private lands in Utah and successfully resolved a potential environmental roadblock by working with local officials, who created a conservation plan for a potentially rare plant. -

It Has Been Widely Acknowledged and Supported by a Range of Empirical Studies That Though Political Democracy Has Positive Effec
VYTAUTAS MAGNUS UNIVERSITY THE FACULTY OF POLITICAL SCIENCE AND DIPLOMACY THE DEPARTMENT OF REGIONAL STUDIES Ana Novikaite INDUSTRIAL LOCATION AND CONCENTRATION: POLITICAL LOGIC BEHIND AUTHORITARIAN LEADER’S REDISTRIBUTIVE POLICIES. THE CASE OF THE PRC Final Master‟s Thesis East Asia Region Studies programme, Code 62602S106 Field of Studies: Political Sciences Supervisor Dr.Vincentas Vobolevicius ____________ _______ (degree, name, surname) (signature) (date) Defended Prof. Sarunas Liekis_______ ___________ _______ (Dean of the Faculty) (signature) (date) Kaunas, 2011 VYTAUTO DIDŽIOJO UNIVERSITETAS POLITIKOS MOKSLŲ IR DIPLOMATIJOS FAKULTETAS REGIONISTIKOS KATEDRA Ana Novikaitė PRAMONĖS GEOGRAFINĖ PADĖTIS IR KONCENTRACIJA: AUTORITARINIO LYDERIO VYKDOMOS PERSKIRSTYMO POLITIKOS LOGIKA. KINIJOS LIAUDIES RESPUBLIKOS ATVEJIS Magistro baigiamasis darbas Rytų Azijos regiono studijų programa, valstybinis kodas 62602S106 Politikos mokslų studijų kryptis Vadovas Dr.Vincentas Vobolevičius __________ ______ (Moks. laipsnis, vardas, pavardė) (parašas) (data) Apginta Prof. Šarūnas Liekis_______ ___________ _______ (PMDF dekanas) (parašas) (data) Kaunas, 2011 CONTENTS Summary (English) .................................................................................................................................. 2 Summary (Lithuanian) ............................................................................................................................. 3 Abbreviations .......................................................................................................................................... -

Research on the Height of Water Flowing Fractured Zone of Fully Mechanized Caving Mining in Extra-Thick Coal Seam
View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Available online at www.sciencedirect.com Procedia Engineering ProcediaProcedia Engineering Engineering 00 (2011 26) (2011)000–000 466 – 471 www.elsevier.com/locate/procedia First International Symposium on Mine Safety Science and Engineering Research on the Height of Water Flowing Fractured Zone of Fully Mechanized Caving Mining in Extra-thick Coal Seam FENG Shaojie a,b,* SUN Shiguo a,b, LV Yuguoc, LV Ji b a School of Soil and Water Conservation,Beijing Forestry University, Beijing 100083,China. b College of Architecture and Civil Engineering, North China University of Technology,Beijing,100144,China. cLaohutai Mine, Fushun Mining Group,Fushun,Liaoning,113008,China Abstract Failure height of overlying rock mass in extra-thick coal seam conditions by fully mechanized caving mining affects the groundwater occurrence condition, which in turn, affects mine safety. Aiming at extra-thick coal seam conditions, this paper numerically stimulates the dynamic process of actual excavation. Results show that failure height increases with excavation volume, thereby increasing the location of abscission layer dropping along with increasing failure height. An abscission layer is formed along the depth, changing the condition of groundwater occurrence and exposing a hidden safety hazard in the field of continuous mining. The simulation results are in line with the fact by verification with drilling survey data. © 2011 Published by Elsevier Ltd. Open access under CC BY-NC-ND license. Selection and/or peer-review under responsibility of China Academy of Safety Science and Technology, China University of Mining and Technology(Beijing), McGill University and University of Wollongong. -

Integration Techniques of Ecological Restoration and Mining in Open Pit Coal Mine
Advances in Engineering Research, volume 63 5th International Conference on Sustainable Energy and Environment Engineering (ICSEEE 2016) Integration Techniques of Ecological Restoration and Mining in Open Pit Coal Mine 1,a 1, b 1,c 1,d 2,e Ziling Song , Dongyang Zhao ,Yuxiang Zhou ,Junfu Fan , Yushi Ji 1Liaoning Technical University, Fuxin City, Liaoning Province, People's Republic of China,123000 2Shenyang Branch of China Coal Research Institute, Fushun City, Liaoning Province, People's Republic of China, 113122 [email protected], [email protected], [email protected],[email protected],[email protected] Keywords: surface coal mine; green mining; Integrated technique; green degree Abstract. The ecological environment problems in open pit mining and the present situation of coal mining are analyzed. The traditional open pit mining aims at pursuing economic interests, which leads to serious ecological environment problems. Open pit mining will cause the comprehensive destruction of the solid environment, water body environment, gas environment and ecological environment. Ecological restoration of opencast mine and mining Integration techniques is an effective way to solve the environmental problems of open-pit mine; Ecological restoration become as an important unit of surface mining technology, and the green mining technology system is formed; It is defined that the open-pit mining technology green system and the composition of technology units; We put forward and defined "green degree" concept and the connotation; Through evaluating the green degree index of open-pit mining, the open pit are promoted using a series of integration technologies for ecological restoration and mining, and the green mining goal is realized; The Integration techniques of open-pit mine ecological restoration and mining include two aspect of open-pit lifecycle integration, and ecological restoration progress and stripping progress. -

World Bank Document
ESM326 Public Disclosure Authorized A Strategy for Coal Bed Methane (CBM) and Mine (CMM) Development Utilization in China 326/07 Report Formal Formal Report 326/07 A Strategy for Coal Bed Public Disclosure Authorized Methane (CBM) and Coal Mine Methane (CMM) Development and Utilization in China Public Disclosure Authorized Energy Sector Management Assistance Program 1818 H Street, NW Washington, DC 20433 USA Tel: 1.202.458.2321 Fax: 1.202.522.3018 Internet: www.esmap.org Email: [email protected] Public Disclosure Authorized Energy Sector Management Assistance Program Energy Sector Management Assistance Program Purpose The Energy Sector Management Assistance Program (ESMAP) is a global technical assistance partnership administered by the World Bank since 1983 and sponsored by bilateral donors. ESMAP's mission is to promote the role of energy in poverty reduction and economic growth in an environmentally responsible manner. Its work applies to low-income, emerging, and transition economies and contributes to the achievement of internationally agreed development goals through knowledge products such as free technical assistance; specific studies; advisory services; pilot projects; knowledge generation and dissemination; training, workshops, and seminars; conferences and round-tables; and publications. The Program focuses on four key thematic areas: energy security, renewable energy, energy poverty, and market efficiency and governance. Governance and Operations ESMAP is governed by a Consultative Group (CG) composed of representatives of the World Bank, other donors, and development experts from regions that benefit from ESMAP assistance. The ESMAP CG is chaired by a World Bank Vice-President and advised by a Technical Advisory Group of independent energy experts that reviews the Program's strategic agenda, work plan, and achievements. -

Power Transmission and Control
POWER TRANSMISSION AND CONTROL International Trade Show for Hydraulics, Pneumatics, Seals, Gears,Motors, Coupling&Brakes, Chains, Belts, Springs, Bearings and Industrial Supply 3-6 November 2020 Shanghai New International Expo Centre 驱动未来 After Show Report Driven to be SMART www.ptc-asia.com Previous review 101,057 professional visitors 233 matchmaking meetings About sqm 70,000 show scale 17 concurrent events buyer Near 130 1,000 delegations exhibitors 2 Previous review The most important annual industry trade fair in Asia Pacific region - PTC ASIA 2020 was concluded successfully on November 6th, 2020 at Shanghai New International Expo Center. The COVID-19 pandemic has brought a sudden challenge to 2020, after the unwillingly “pause button” was pushed for six months, the recovery process of the industry started. PTC ASIA 2020 attracted nearly 1,000 well-known exhibitors, covered 70,000sqm show area, and showcased new intelligent manufacturing achievements post the pandemic impact. The four-day show accommodated 101,057 trade visitors in total, the number was comparably higher than the 2018 edition which had similar show scale. Most of the exhibitors thought the visitors this year were more professional and accurate than last year. Over 130 buyers delegations from China Shendong Group under China Energy Group, Shanghai Electronic Group, Beiqi New Energy Vehicle Group, China Space Sanjiang Group, Bao Steel, BYD, Shanghai Machine Tool Co., Ltd., Suzhou Hamco, Cotek Robotics, Pan Asia, LS Heavy Machinery, KUKA, WEIFU, Eurocrane, CSSC Heavy -
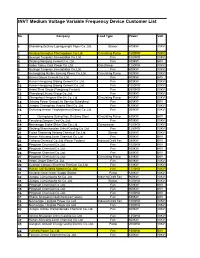
INVT Medium Voltage Variable Frequency Device Customer List
INVT Medium Voltage Variable Frequency Device Customer List No. Company Load Type Power Volt. 1 Shandong Dezhou Lupingyongfa Paper Co.,Ltd. Blower 400KW 10KV 2 Xinjiang Guanghui Thermopower Co.,Ltd. Circulating Pump 1600KW 10KV 3 Guangxi Tengxian Jinmaotaibai Co.,Ltd. Fan 1000KW 10KV 4 Xinjiang Nangang Cement Co.,Ltd. Fan 800KW 6KV 5 Hebei Tianyu Coal Power Co.,Ltd. Gas Blower 1250KW 10KV 6 Guangxi Tengxian Jinmaotaibai Co.,Ltd. Fan 400KW 10KV 7 Heilongjiang Harbin Jieneng Power Co.,Ltd. Circulating Pump 500KW 10KV 8 Gansu Gaoya Cement Co.,Ltd. Fan 800KW 6KV 9 Hunan Hengyang Qidong Cement Co.,Ltd. Fan 800KW 10KV 10 Hunan Hengyang Qidong Cement Co.,Ltd. Fan 1000KW 10KV 11 Hebei Steel Group (Yongyang Factory) Fan 2500KW 10KV 12 Shandong Lihuayi Group Co.,Ltd. Fan 500KW 10KV 13 Zhengzhou Hengxun Electric Co.,Ltd. Circulating Pump 400KW 10KV 14 Jizhong Power Group(Life Service Subsidiary) Fan 800KW 6KV 15 Jiangsu Changzhou Huaxia Steel Co.,Ltd. Fan 630KW 10KV 16 Sichuang Anxian Yinghejianhua(Group) Co.,Ltd. Fan 500KW 10KV 17 Guangdong Guangzhou Zhujiang Steel Circulating Pump 630KW 6KV 18 Fengfeng Zongxin CoalCo.,Ltd. Co.,Ltd. Fan 500KW 10KV 19 Neimenggu Etoke Shitai Gas Co.,Ltd. Compressor 1600KW 10KV 20 Xinjiang Shanshanxian Jinhui Casting Co.,Ltd. Fan 1250KW 10KV 21 Fujian Shanming Xinlong Chemical Co.,Ltd. Blower 630KW 10KV 22 Henan Xichuang Jiuxin Chemical Co.,Ltd. Fan 500KW 6KV 23 Yizheng Chemical Co.,Ltd.(Power Factory) Induced Draft Fan 280KW 6KV 24 Pingyuan Chemical Co.,Ltd. Fan 1000KW 6KV 25 Pingyuan Chemical Co.,Ltd. Fan 500KW 6KV 26 Pingyuan Chemical Co.,Ltd. -

EMD Oil Shale Committee
EMD Oil Shale Committee 2016 EMD Oil Shale Committee Final Report Alan K. Burnham (Chair), Stanford University May 18, 2016 Vice-Chairs: Dr. Mariela Araujo (Vice-Chair: Industry), Shell International Exploration and Production Dr. Lauren Birgenheier (Vice-Chair: University), University of Utah Dr. Justin E. Birdwell (Vice-Chair: Government), U.S. Geological Survey Advisory Group: Dr. Jeremy Boak, Oklahoma Geological Survey, University of Oklahoma Mr. Ronald C. Johnson, U.S. Geological Survey Special Consultants to the Committee: Robert Kleinberg, Schlumberger-Doll Research Steven Kerr, Millcreek Mining Group Jaanus Purga, Viru Keemia Grupp (VKG) Rikki Hrenko-Browning, Enefit American Oil Indrek Aarna, Eesti Energia Steven Odut, Thyssenkrupp Gary Aho, Sage Geotech Pierre Allix, Total S.A. John Parsons, QER Pty Ltd Gerald Daub, Daub & Associates, Inc. EXECUTIVE SUMMARY Progress on oil shale continued around the world, although many projects have been cancelled recently due to low oil prices. New production capacity was in full force in Estonia and China, and plans for production moved forward in Jordan and Utah, although at a slower pace than expected a few years ago. Some companies are re-optimizing their processes and projects to adapt to the current economic situation. The current status is still in flux, and it is too early to know whether we are seeing a repeat of the 1980s or a shorter-term correction. Oil shale continues to be mined and retorted or burned in power plants in Estonia, China and Brazil. Production rose significantly in 2015, but future expansion is uncertain. In Estonia, Viru Keemia Grupp brought a second Petroter plant on line in Q3 of 2014 and a third unit in the Q3 of 2015, 1 bringing their total installed capacity to ~14,000 BOPD (barrels of oil per day). -

EMD Oil Shale Committee
EMD Oil Shale Committee EMD Oil Shale Committee Annual Report – 2014 Alan Burnham, Chair November 17, 2014 Vice-Chairs: Dr. Lauren Birgenheier (Vice-Chair – University) University of Utah Mr. Ronald C. Johnson (Vice-Chair – Government) U.S. Geological Survey Dr. Mariela Araujo (Vice-Chair – Industry) Shell International Exploration and Production Highlights Progress on oil shale continued in both the United States and around the world, but with a greater sense of urgency in countries with lesser quantities of conventional energy sources. New production capacity was brought on line in Estonia and China, and plans for production this decade moved forward in Jordan. In the U.S., the Utah Division of Water Quality issued a groundwater permit to Red Leaf Resources, which now has the go-ahead to establish a small-scale commercial production system based on the EcoShale process as a joint venture with Total. A challenge by environmental groups was settled by allowing access to groundwater monitoring data. TomCo also applied for permits to establish a commercial operation using the EcoShale process 15 miles from the Red Leaf operation. Enefit made progress getting permits development of its private lands in Utah and successfully resolved a potential environmental roadblock by working with local officials to create a conservation plan for a potentially rare plant. For the U.S. Bureau of Land Management (BLM) Research, Development, and Demonstration (RD&D) leases, Enefit USA and American Shale Oil LLC continued efforts to demonstrate their oil shale processes, with the goal of conversion to a commercial lease. Natural Soda Holdings Inc. and ExxonMobil received approval of their Plans of Development for the second round of RD&D Leases.