DOCSLIB.ORG

The Integral Role of Phytoplankton Stoichiometry in Ocean Biogeochemical Dynamics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
The Integral Role of Phytoplankton Stoichiometry in Ocean Biogeochemical Dynamics The integral role of phytoplankton stoichiometry in ocean biogeochemical dynamics A Dissertation SUBMITTED TO THE FACULTY OF THE UNIVERSITY OF MINNESOTA BY Tatsuro Tanioka IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY Katsumi Matsumoto November, 2019 © Tatsuro Tanioka 2019 ALL RIGHTS RESERVED Acknowledgements I would like to thank my advisor Katsumi Matsumoto who has given me the best ad- vice and encouragement whenever I needed. I am also grateful to the members of my committee- Jake Bailey, Jim Cotner, and Bill Seyfried for their time and energy. I would also like to thank Kathy Tokos for helping me with MESMO. This work was supported by student fellowships from the Earth Sciences Department, Doctoral Dissertation Fel- lowship from the University of Minnesota Graduate School, and by NSF grant awarded to Dr. Katsumi Matsumoto. Thank you to all my friends and colleagues from the de- partment and outside the department; and to my teammates from the Australian Rules Football Team, Minnesota Freeze. Finally, thank you to my family for their support over the years. Tatsuro Tanioka November, 2019 i Dedication To my life-coach, my late grandfather Mitsugu. ii Abstract Photosynthesis by ocean algae (phytoplankton) contributes roughly half of the earth's net carbon production. Organic matter produced using carbon dioxide in the atmosphere not only supports marine food webs, but also acts as a climate stabilizer, because carbon is subsequently transported to the deep ocean and stored there for thousands of years. Attempts to model global marine biological production and its impacts on global biogeochemical cycles often assume a constant elemental stoichiometry of carbon, nitro- gen, and phosphorus in phytoplankton biomass. This ratio, known as the Redfield ratio, was determined on the basis of an analysis of many samples of marine plankton collected over 70 years ago. This notion is well established in the oceanographic community but there is no clear physiological justification for why the C:N:P ratios in phytoplankton should strictly follow the Redfield ratio. Many recent studies revealed that C:N:P ra- tio of particulate organic matter can deviate significantly from the Redfield Ratio with some noticeable spatial and temporal variability. Studies suggest that factors such as nutrient availability, light, and temperature play a crucial role in modifying C:N:P ratio of phytoplankton. In this dissertation, I investigate the roles of marine phytoplankton stoichiometry in the global marine biogeochemical dynamics by combining meta-analysis, numerical modeling, and remote sensing. I propose a mechanistic framework for predicting C:N:P in phytoplankton under different environmental conditions and I incorporate this frame- work into an Earth System Model to show their effects on global carbon cycle. I also present results on how the change in elemental composition of phytoplankton could af- fect the feeding behavior of zooplankton as well the ecosystem stoichiometry. Finally, I show that C:N:P is closely tied to the rate at which oxygen is consumed during organic matter remineralization and I propose that the change in phytoplankton stoichiometry could ameliorate the rate of marine deoxygenation. In summary, C:N:P of phytoplankton is flexible and will play key roles in future global ocean biogeochemical dynamics. iii Contents Acknowledgements i Dedication ii Abstract iii List of Tables viii List of Figures ix 1 Introduction 1 1.1 Overview of Chapters . 2 2 Phytoplankton stoichiometry and global export production 4 2.1 Synopsis . 4 2.2 Introduction . 5 2.3 New Stoichiometry Sensitivity Factor . 7 2.3.1 Derivation . 7 2.3.2 Estimation of Parameters . 10 2.3.2.1 Nonlinear Least Squares Regression . 11 2.3.2.2 Estimation of Parameters from First Principles . 12 2.4 First-Order Estimation of Global Stoichiometric Buffer Effect . 13 2.5 Flexible Stoichiometry in a Global Ocean Model . 16 2.5.1 Model Description . 17 2.5.2 Model Results . 22 iv 2.6 Conclusions . 25 2.7 Acknowledgments . 26 3 Environmental drivers of phytoplankton stoichiometry: a meta-analysis 27 3.1 Synopsis . 27 3.2 Introduction . 28 3.3 Materials and Methods . 30 3.3.1 Bibliographic search and screening . 30 3.3.2 Stoichiometry sensitivity factor as effect size . 32 3.3.3 Meta-analysis . 33 3.4 Results . 34 3.4.1 Effects of Phosphate . 34 3.4.2 Effects of Nitrate . 35 3.4.3 Effects of Nitrate:Phosphate supply ratio . 35 3.4.4 Effects of Irradiance . 35 3.4.5 Effects of Temperature . 37 3.4.6 Effects of Iron . 37 3.5 Discussion . 37 3.5.1 Basic framework . 37 3.5.2 Macronutrients (Phosphate and Nitrate) . 43 3.5.3 Irradiance . 45 3.5.4 Temperature . 47 3.5.5 Iron . 49 3.6 Implications for global biogeochemical cycles . 50 3.6.1 Conclusions . 53 3.6.2 Acknowledgements . 54 4 Phytoplankton stoichiometry and feeding behavior of zooplankton 55 4.1 Synopsis . 55 4.2 Introduction . 56 4.3 Method . 57 4.3.1 C:N:P as a function of age . 59 4.3.2 Maximum assimilation rate as a function of age . 60 v 4.3.3 Flexible grazing preference as a function of age . 62 4.3.4 Experimental setup . 65 4.4 Results . 66 4.5 Discussion . 70 4.6 Acknowledgments . 71 5 Phytoplankton stoichiometry and organic matter respiration 72 5.1 Synopsis . 72 5.2 Introduction . 73 5.3 Methods . 75 5.3.1 Estimating O2:C from satellite-dericed phytoplankton macromolec- ular composition . 75 5.3.2 Estimating O2:C from the vertical gradient method of dissolved nutrients and oxygen . 76 5.3.3 Estimating O2:C from laboratory and in situ measurements of phytoplankton macromolecules . 77 5.3.4 Monte Carlo simulation . 78 5.4 Results and Discussion . 79 5.5 Implications for the Future Marine Oxygen Cycle . 84 5.6 Acknowledgments . 86 6 Concluding Remarks 88 References 91 Appendix A. Supporting Information For Chapter 2 126 Appendix B. Supporting Information For Chapter 3 128 Appendix C. Supporting Information For Chapter 4 130 Appendix D. Supporting Information For Chapter 5 131 D.1 Uncertainties associated with O2:C remineralization ratio calculated from the satellite-derived estimate of macromolecules . 132 D.2 Derivation of equation(5.4) in the main text . 132 vi D.3 Assumptions and limitations of the vertical gradient method . 134 D.4 Validating the vertical gradient method . 134 vii List of Tables 2.1 Comparison of Flexible P:C Formulations . 9 2.2 Model Parameters for the Preindustrial and Transient Simulation . 18 2.3 Model Results for the Preindustrial and Transient Simulations . 23 3.1 Breakdown of the number of experimental units . 32 3.2 Summary of s-factors for P:C and N:C . 41 3.3 Projected change in C:P and C:N between 1981-2000 and 2081-2100 . 51 B.1 List of 64 studies used in the meta-analysis . 128 C.1 Default food preference of mesozooplankton in the original ERSEM model130 D.1 Assumed elemental composition of main phytoplankton macromolecules obtained from literatures . 145 D.2 Uncertainties in satellite-derived estimate of macromolecules . 145 D.3 Effects of changing percent fraction of nucleic acid in estimating O2 :Crem from the satellite-derived estimate of phytoplankton macromolecules . 146 D.4 Summary of macromolecular data from Roy (2018) . 147 D.5 O2 :Crem from 9 sensitivity analyses accounting for seasonal variability and depth choice . 148 viii List of Figures 2.1 Observed particulate P:C versus surface PO4 concentrations . 11 2.2 Stoichiometry sensitivity factor against PO4 . 14 2.3 Change in export production from 1990s as a function of the fractional change in PO4 from 1990s . 16 2.4 Modeled community stoichiometry sensitivity factor under preindustrial condition . 19 2.5 Modeled nutrient limitation under preindustrial condition in the surface layer...................................... 20 2.6 Modeled C:P and N:P of phytoplankton in the surface layer . 21 2.7 Simulated changes in surface PO4 and total export production in 2090s relative to 1990s . 22 2.8 Results from a global ocean model under IPCC RCP8.5 scenario . 25 3.1 low chart showing the preliminary selection criteria and the refined se- lection criteria used for determining s-factors . 31 3.2 S-factors for P:C and N:C with respect to changes in macronutrients . 36 3.3 S-factors for P:C and N:C with respect to changes in irradiance . 38 3.4 S-factors for P:C and N:C with respect to changes in temperature . 39 3.5 S-factors for P:C and N:C with respect to changes in iron . 40 3.6 Illustration of how the five environmental drivers under a typical future climate scenario affect the cellular allocation . 43 4.1 Biogeochemical model ERSEM used in simulations . 58 4.2 C:N:P ratios and maximum assimilation rate during copepod ontogeny . 61 4.3 Schematic diagram showing the effect of food quality on food preference of copepod (mesozooplankton) . 64 ix 4.4 Equilibrium biomass of plankton functional types as a function of meso- zooplankton N:P ratio . 67 4.5 Equilibrium food preference of mesozooplankton as a function of meso- zooplankton N:P ratio . 68 4.6 N:P ratio of released nutrient and large POM as a function of mesozoo- plankton N:P ratio . 69 5.1 Satellite-derived annually averaged phytoplankton macromolecular con- tent and O2:C remineralization ratio binned into 11 oceanographic regions 80 5.2 Export and remineralization ratios determined from the vertical gradient method . 81 5.3 O2 :Crem estimated from laboratory-based measurements of phytoplank- ton macromolecule content . 83 5.4 O2 :Crem in various marine ecosystems estimated from biochemical com- position of phytoplankton .
Load more

Recommended publications
  • Students Work Overseas Through CIEE Tuition Costs. to Increase For
    of energy, Library materials and other items that have risen faster then inflation, facility renovation, and the need to replace federal funds that are no longer available as reasons for the increase. She started that salaries have failed to keep pace with the Con- sumer Price Index in the past years and salary increases are needed because "we cannot compete with Student Publication • corporate salries" and added that Vol. 19, No. 7 of Concordia Col lege, St. Paul, MN. "dedication is needed for people to work here." Marken pointed out that. Concor- centers and industrial states where dia's tuition continues to be the lowest Students Sought for millions are unregistered. of all the private colleges in Min- Freedom Summer Registration nesota and students receive a larger Voter Registration sites include: California, Connecticut, amount of financial aid here. Students Colorado, Georgia, Florida, Illinois, Students Work contribute only 61% of Concordia's lima, Louisiana, Maryland, total revenue. Tuition and fees make Drive Massachusetts, Michigan, Missouri, Overseas up 43%, room and board accounts for New Jersey, New York, New Mexico, 17%, and 1% comes from student ac- College campuses across the coun- North Carolina, Ohio,. Pennsylvania, tivities. Of the remaining 39%, 19% try are the focus of a massive student Tennessee, Texas and Virginia. For Through CIEE comes from Synod, 9% comes in the recruitment drive for an un- more information on volunteer form of grants and gifts, 1% is federal precedented voter registration cam- registration, contact: USSA-NSEF and state aid, and 10% comes from paign aimed at registering one 202-775-8943/202-785-1856 or Human other sources.
    [Show full text]
  • 2013 Annual Report
    UNITED STATES AUSTRALIAN FOOTBALL LEAGUE 2013 Annual Report usafl.com UNITED STATES AUSTRALIAN FOOTBALL LEAGUE // 2013 Annual Report // A 501(c)3 Not-For-Profit Organization ≈ TABLE OF CONTENTS President’s Address 3 USAFL Structure 4 2013 National Championships 7 USAFL Awards 8 2013 49th Parallel Cup 12 AFL Combine 18 Umpires Report 20 Communications Report 22 Financial Management 23 2014 USAFL Contact List 27 Cover Photo: USAFL Club Captains at 2013 USAFL National Tournament Photographer: Amy Bishop - 2 - UNITED STATES AUSTRALIAN FOOTBALL LEAGUE // 2013 Annual Report // A 501(c)3 Not-For-Profit Organization ≈ 2013 President’s Address uring 2013, the USAFL Executive Board focused • Creation of a board handbook detailing all Don instituting best practices for non-profits and league policies, procedures, and roles creating systems to uphold league rules and reg- • Transition and organization of league docu- ulations/policies. While the league hovers around ments to Google Drive for enterprise man- 1,000 annual members, the USAFL is advancing as agement. an organization. As a better organization we can be While not officially, participation numbers have con- poised for more league growth. We must have one tinued to grow at a local level with metro and co-ed before the other. leagues across the country. Golden Gate, Portland, Baltimore-Washington, and Chicago are examples The past 24 months board activities focused on the of strong metro communities and recently, co-ed non-profit aspect of the league ensuring the organi- leagues have formed in Sacramento, Denver, and zation is well prepared to answer the IRS if an audit Columbus.
    [Show full text]
  • US Footy Ten Year Commemorative Book
    US Footy Ten Year Commemorative Book The First Ten Years of Australian Rules Football in America. “For the good of the game, for the love of the game” USFOOTY United States Australian Football League A REAL USFOOTY THANKS TO President’s Report “If you dream it, you can do it.” Walt Disney Over ten years ago a group of ten Australians and Americans met in a barn in Indiana over a beer or two and dreamed about starting an Australian Rules Football League in the USA. From this gathering and the hard work of many, the USAFL celebrates its tenth year of operation. A dream became a reality and a game born in Australia is quickly establishing itself as a strong minor sport in the land of professional sport. Our tenth National Championships are being played in the city where the first game was played - Louisville, Kentucky. Our Championships have grown over the years from a small gathering of clubs to a significant number that produce economic benefits to the host club and city, but more importantly the gathering of teams is a chance to celebrate football and the league on an annual basis. If you haven’t been to the USAFL Championships you are missing a great celebration of grass roots sport. At these Championships we will celebrate those players, coaches, umpires and officials who have been integral to the success of the USAFL. We will remember past matches and past Championships. The stories will be told of those fantastic road trips and the characters that make being part of a football team one of the great experiences of life.
    [Show full text]
  • 2013 Year in Review
    Table of Contents Chaska Juniors 12-Black 3 Lucia Saathoff 42 Chaska Juniors 12-1 4 Dana Schindler 43 Chaska Juniors 14-1 5 Erin Schindler 44 Chaska Juniors 15-1 6 Keena Seiffert 45 Chaska Juniors 16-1 9 Lindsay Snuggerud 46 Chaska Juniors 17-1 13 Morgan Solie 47 Makenzie Bachmann 15 Danielle Sons 48 Emma Baker 16 Geena VanVooren 49 Amber Carlson 17 Sam Weller 50 Alicia Costa-Terryll 18 Makayla Wenzel 51 Molly Delander 19 Monica Ziebell 52 Molly Frank 20 Nicki Dutoit/Vicki Herman 53 Nicole Hansen 21 Chuck Zemek/Ben Wallerus 54 Bailey Harms 22 Michael Hull/Nolan Mitchell 55 Nicole Harrison 23 Mike Murphy/Anne DeSautel 56 Carly Hendrickson 24 Chelsey Earney/Marnie Pauly 57 Colee Hennen 25 Sue Murphy 58 Elizabeth Hoppe 26 Chaska Juniors vs Opponents • 2013 59 Mikayla Johnson 27 Team Top Finishes 60 Sarah Kelly 28 All-Americans 61 Jordan Knapp 29 Chaska Juniors in the Community 62 Lily Lark 30 Sarah Marshall 31 Jennifer Mueller 32 Lauren Nordvold 33 Siri Olson 34 Caroline Orwoll 35 Anna Panning 36 Lindsey Pollock 37 Megan Purdy 38 Ingrid Rischmiller 39 Denae Rothmeier 40 Molly Rudie 41 2 Roster # Name Year Height Pos. 2 Lainey Borner 3 4-6 S 5 Sydney Huwe 4 4-10 S 9 Ellexis Grochow 6 5-5 S 11 Katie Winslow 4 5-0 S 12 Montana Kack 4 4-10 S 13 Erika Schmidt 5 5-1 S 14 Ella Christ 3 4-8 S 16 Julia Dumcum 4 4-11 S 22 Eleanor Smith 3 4-9 S 35 Raissa Gebauer 4 4-10 S Front Row (L-R): Ella Christ, Eleanor Smith, Head Coach Nicki DuToit, Rais- Head Coach: Nicki DuToit sa Gebauer, Sydney Huwe.
    [Show full text]
  • Athletic Fields Designed Near Nokomis, Urban Ag Proposed Near
    Lake + Minnehaha Unique business makes Community Oven Open Streets cider out of foraging tops Eagle Scout planned for July 23 for fruit accomplishments PAGE 5 PAGE 7 PAGE 12 July 2017 Vol. 33 No. 5 www.LongfellowNokomisMessenger.com 21,000 Circulation • Athletic fields designed near Nokomis, urban ag proposed near Hiawatha Open house held as changes require modifi cation of Nokomis-Hiawatha Regional Park by park board By TESHA M. CHRISTENSEN there as well. With the focus of nearby “It would be great to have the Bossen Park on softball, some resi- men’s and women’s teams practice dents feel that leaves room for other together,” noted Freeze Captain An- sports such as Australian Football drew Werner, a Nokomis resident, and soccer at Nokomis Park. but it is diffi cult to do now because The current project at Bossen of how the fi elds are arranged. “The is placing four premier baseball/ sport is community-based,” he ob- softball fi elds in a pinwheel forma- served. “A lot of families come out tion looking out, with another two and watch, too.” Plus, they’d like to fields on the south side and two see the club grow. large open fi eld areas on the north. The groups need fi elds that are When the Nokomis-Hiawatha larger than soccer fi elds, such as two Regional Park master plan was ap- soccer fields side-by-side, to play proved in March 2015, it didn’t in- a game. The Gaelic team can’t use clude a specifi c layout for the ath- Minneapolis Parks and Recre- the fi elds as they are now due to the Minnesota Freeze men’s team captain Andrew Werner discusses athletic letic fi elds, in part because planners ation Board employee Siciid Ali number of potholes, unlevel surfac- fi eld confi gurations with fellow football and hurling players during an open knew that the Bossen Field project (left) discusses possible changes es, and gopher holes.
    [Show full text]
  • US Footy Ten Year Commemorative Book
    US Footy Ten Year Commemorative Book The First Ten Years of Australian Rules Football in America. “For the good of the game, for the love of the game” USFOOTY United States Australian Football League A real USFooty thanks to: President’s Report “If you dream it, you can do it.” Walt Disney Over ten years ago a group of ten Australians and Americans met in a barn in Indiana over a beer or two and dreamed about starting an Australian Rules Football League in the USA. From this gathering and the hard work of many, the USAFL celebrates its tenth year of operation. A dream became a reality and a game born in Australia is quickly establishing itself as a strong minor sport in the land of professional sport. Our tenth National Championships are being played in the city where the first game was played - Louisville, Kentucky. Our Championships have grown over the years from a small gathering of clubs to a significant number that produce economic benefits to the host club and city, but more importantly the gathering of teams is a chance to celebrate football and the league on an annual basis. If you haven’t been to the USAFL Championships you are missing a great celebration of grass roots sport. At these Championships we will celebrate those players, coaches, umpires and officials who have been integral to the success of the USAFL. We will remember past matches and past Championships. The stories will be told of those fantastic road trips and the characters that make being part of a football team one of the great experiences of life.
    [Show full text]
  • Management Internship History
    Management Internship History Site Location Intern's Title Term Year 3M Center, Bldg 220-2E-05 St. Paul Finance Intern Summer 2009 Acheson Tire Incorporated Grand Rapids Inventory Control Intern Summer 2012 ActionAid International Washington, DC Finance & Marketing/Development Intern Summer 2008 Activity Tree Mendota Heights Sales Representative Fall 2011 Advance Well Systems Big Lake Estimator, Salse Summer 2007 Aerosur Miami Marketing Assistant Fall 2011 Aerosur Miami Marketing Assistant Summer 2011 Aerotek Arden Hills Recruiter Summer 2011 AeroTek Maple Grove Management Intern Summer 2009 Agency 128 St. Cloud Comm Intern Spring 2010 Akros Company New York Investment Management Intern Summer 2009 Albany Chrysler Center Albany Finance Assistant Inventory Summer 2011 Albany Senior High School Albany Athletic Intern Spring 2008 Alexandria Blizzard Hockey Alexandria Sales/Marketing and Game Operations Assistant Summer 2008 All American Foods, Inc. Mankato Sales and Marketing Intern Summer 2009 All Over Media St. Joseph Assistant Manager Summer 2008 All Over Media St. Joseph Marketing and Sales Intern Summer 2007 Allied Building Products Brooklyn Center Sales Intern Summer 2012 ALSAC/St. Jude's Children Research Hospital Edina Event Marketing Intern Summer 2007 American Combat Academy ST. Cloud Assistant Summer 2010 American Family Insurance Maple Grove Maple Grove Insurance Assistant Spring 2008 American Family Insurance Maple Grove Maple Grove Sales Assistant Summer 2007 Page 1 of 28 Site Location Intern's Title Term Year Ameriprise Financial, Inc. Minneapolis Finance Intern Summer 2008 Ameriprise Financial-St. Cloud St. Cloud Financial Intern Spring 2012 Annual Giving Office St. Joseph Annual Fund Student Worker Fall 2007 Annual Giving Office St. Joseph Annual Giving Intern Spring 2012 Aon Global Bloomington Risk Management/Global Accounts Intern Summer 2012 Aramark St.
    [Show full text]
  • Dante Weightlifting 2015
    + TUESDAY, 2015 MARCH 24, Heavy metal Olympic lifting gains momentum IF IT MATTERS TO YOU, IT MATTERS TO US Connect with us at Postbulletin.com Four sections I 75( City approves DMC development plan BY ANDREW SEnERHOLM Inside and other parts of the world, [email protected] none of which have the Next steps The Rochester City Coun­ Plan funding hits a speed background or the history we cil did its part to advance bump.A2 have," he said. DMC development plan process: Destination Medical Center DMC administrative costs bill Smithson asked that the ·Approval by city council (March 23). plan be looked at again, with plans Monday evening with clears Senate committee. AS • DMCC public hearing on development plan (April23). the approval of a long-term, steps more clearly sketched conceptual development plan. out. • DMCC board adoption of the development plan. The council was unani­ of the plan such as the fate of In all, more than 20 pub- ·City council second hearing on funding source for DMC (May). mous in its approval of the the public librar y to over­ lic comments were offered. • DMCC annual budget and capital improvement plan budget plan, a lengthy document laid Campion Adkins arching goals and effects of Council members, in discus­ submitted to city council (Sept. 1) the plan. sion following the comments, out by consultants working ·City council approva l of DMCC budget for 2016 (December). through the DMC Economic pion said. "I looked at the plan ... and reiterated that the plan Development Agen cy. Council The council's decision I was devastated that the would be a framework for • DMCC, DMC EDA and city council discussions regarding members expressed excite­ came during a meeting held library was going to move," development, not a binding potential public infrastructure projects and private projects (April ment to be taking real action at the Mayo Civic Center Carol Fishbune said.
    [Show full text]
  • The Urban Politics of Settler-Colonialism
    THE URBAN POLITICS OF SETTLER-COLONIALISM: ARTICULATIONS OF THE COLONIAL RELATION IN POSTWAR MINNEAPOLIS, MINNESOTA, 1945-1975 (AND BEYOND) DAVID W. HUGILL A DISSERTATION SUBMITTED TO THE FACULTY OF GRADUATE STUDIES IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY GRADUATE PROGRAM IN GEOGRAPHY YORK UNIVERSITY TORONTO, ONTARIO June 2015 © David Warren Hugill, 2015.! ABSTRACT This dissertation documents some of the ways that colonial practices and mentalities have shaped relationships between Indigenous and non-Indigenous people in the historical and material conjuncture of Minneapolis, Minnesota, with a focus on the period 1945 to 1975. Building on political and geographical literature concerned with the enduring effects of settler-colonization in North American urban environments, my inquiry starts from the premise that the “colonial relation” retains a persistent structural trace in Minneapolis, manifesting through a series of practices and dynamics that operate to enforce particular forms of social, economic, and territorial domination. I begin by demonstrating that Indigenous peoples in the area were territorially and economically displaced in the construction of the newcomer settlement that became Minneapolis, which I describe by looking critically at the life of one of the city’s early “city builders,” Thomas Barlow Walker. I then expand this discussion by developing a series of arguments that demonstrate how the “colonial relation” has articulated in the Phillips neighborhood of South Minneapolis,
    [Show full text]
  • Executive Board Annual Report 2017
    United States Australian Football League A 501(C)3 Not-For-Profit Organization UNITED STATES AUSTRALIAN FOOTBALL LEAGUE Executive Board Annual Report 2017 UNITED STATES AUSTRALIAN FOOTBALL LEAGUE A 501(C)3 Not-For-Profit Organization Table of Contents Year in Review ................................................................................................................................. 3 USAFL Clubs ..................................................................................................................................... 5 USAFL Structure .............................................................................................................................. 6 Regional Championships ................................................................................................................. 7 AFL International Cup ................................................................................................................... 10 National Championships ............................................................................................................... 22 Financial Management ................................................................................................................. 34 2018 USAFL Contact List ............................................................................................................... 42 2 UNITED STATES AUSTRALIAN FOOTBALL LEAGUE A 501(C)3 Not-For-Profit Organization Year in Review This is the story of season 2017; its ups, its downs, and the continued passion
    [Show full text]
  • Minnesota Freeze Win 2012 U.S. National Championship
    Minnesota Freeze Win 2012 U.S. National Championship Australian Rules Football is alive and well in Minnesota St. Louis Park, MN (Oct.18, 2012) – The Minnesota Freeze Australian Rules Football Club (The Freeze) celebrates its 3rd National Championship with their Division 2 Men’s team finishing off the Los Angeles Dragons in their final match this past weekend in Mason, Ohio. The final score was 12-3. This year’s United States Australian Football League (USAFL - www.usafl.com) National Championships were held in Mason, Ohio, bringing together over 50 clubs to compete in 4 men’s and a women’s division. The Freeze brought three teams to the tourney: a Division 2 and 4 men’s team and a women’s team. 50 players suited up to represent Minnesota at this tournament. While all three teams played fearlessly in their matches, the men’s Division 2 team went the distance, winning all three qualifying matches (vs. Boston Demons, Austin Crows and San Diego Lions) to earn the right to compete in the Grand Final. Individual tournament honors were also garnered by Freeze players. We congratulate Zach Weaver for winning the coveted Division 2 “Most Consistent” award. Stephen Fashant took home the Division 2 Final’s MVP award. Both men also represented the US at last year’s International tournament, held in Australia. The Freeze provided a significant contingent to both the US Men’s team (Revolution) and Women’s team (Freedom). (http://www.usafl.com/usateams) Australian Rules Football (“footy”) is growing nation-wide and, despite the weather induced limited season, the Minnesota Freeze have established themselves as a hotbed for quality play and sportsmanship.
    [Show full text]
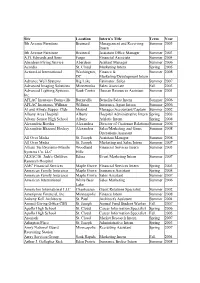
  • Management Table
    Site Location Intern’s Title Term Year 5th Avenue Furniture Brainerd Management and Receiving Summer 2003 Intern 5th Avenue Furniture Brainerd Assistant Office Manager Summer 2003 A.G. Edwards and Sons Fargo Financial Associate Summer 2004 Aberdeen Flying Service Aberdeen Assitant Manager Summer 2006 Acordia St. Cloud Marketing Intern Spring 2005 ActionAid International Washington, Finance & Summer 2008 DC Marketing/Development Intern Advance Well Systems Big Lake Estimator, Sales Summer 2007 Advanced Imaging Solutions Minnetonka Sales Associate Fall 2003 Advanced Lighting Systems, Sauk Centre Human Resources Assistant Summer 2001 Inc. AFLAC Insurance Burnsville Burnsville Benefits Sales Intern Summer 2006 AFLAC Insurance Willmar Willmar Insurance Agent Intern Summer 2006 Al and Alma's Supper Club Mound Manager/Accountant/Captain Summer 2002 Albany Area Hospital Albany Hospital Administrative Intern Spring 2003 Albany Senior High School Albany Athletic Intern Spring 2008 Alexandria Beetles Alexandria Director of Customer Relations Summer 2006 Alexandria Blizzard Hockey Alexandria Sales/Marketing and Game Summer 2008 Operations Assistant All Over Media St. Joseph Assistant Manager Summer 2008 All Over Media St. Joseph Marketing and Sales Intern Summer 2007 Alliant TechSystems-Missile Woodland Financial Services Intern Summer 2003 Systems Co. LLC Hills ALSAC/St. Jude's Children Edina Event Marketing Intern Summer 2007 Research Hospital AMC Financial Services Maple Grove Financial Services Intern Spring 2003 American Family Insurance Maple Grove Insurance Assistant Spring 2008 American Family Insurance Maple Grove Sales Assistant Summer 2007 American International White Bear Sales Marketing Summer 2006 Lake AmericInn International LLC Chanhassen Guest Relations Specialist Summer 2002 Ameriprise Financial, Inc. Minneapolis Finance Intern Summer 2008 Ankeny Kell Architects St.
    [Show full text]