Web Feature 2.2 1
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
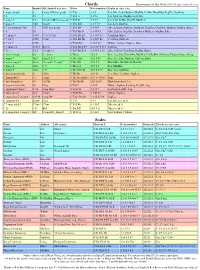
Chords and Scales 30/09/18 3:21 PM
Chords and Scales 30/09/18 3:21 PM Chords Charts written by Mal Webb 2014-18 http://malwebb.com Name Symbol Alt. Symbol (best first) Notes Note numbers Scales (in order of fit). C major (triad) C Cmaj, CM (not good) C E G 1 3 5 Ion, Mix, Lyd, MajPent, MajBlu, DoHar, HarmMaj, RagPD, DomPent C 6 C6 C E G A 1 3 5 6 Ion, MajPent, MajBlu, Lyd, Mix C major 7 C∆ Cmaj7, CM7 (not good) C E G B 1 3 5 7 Ion, Lyd, DoHar, RagPD, MajPent C major 9 C∆9 Cmaj9 C E G B D 1 3 5 7 9 Ion, Lyd, MajPent C 7 (or dominant 7th) C7 CM7 (not good) C E G Bb 1 3 5 b7 Mix, LyDom, PhrDom, DomPent, RagCha, ComDim, MajPent, MajBlu, Blues C 9 C9 C E G Bb D 1 3 5 b7 9 Mix, LyDom, RagCha, DomPent, MajPent, MajBlu, Blues C 7 sharp 9 C7#9 C7+9, C7alt. C E G Bb D# 1 3 5 b7 #9 ComDim, Blues C 7 flat 9 C7b9 C7alt. C E G Bb Db 1 3 5 b7 b9 ComDim, PhrDom C 7 flat 5 C7b5 C E Gb Bb 1 3 b5 b7 Whole, LyDom, SupLoc, Blues C 7 sharp 11 C7#11 Bb+/C C E G Bb D F# 1 3 5 b7 9 #11 LyDom C 13 C 13 C9 add 13 C E G Bb D A 1 3 5 b7 9 13 Mix, LyDom, DomPent, MajBlu, Blues C minor (triad) Cm C-, Cmin C Eb G 1 b3 5 Dor, Aeo, Phr, HarmMin, MelMin, DoHarMin, MinPent, Ukdom, Blues, Pelog C minor 7 Cm7 Cmin7, C-7 C Eb G Bb 1 b3 5 b7 Dor, Aeo, Phr, MinPent, UkDom, Blues C minor major 7 Cm∆ Cm maj7, C- maj7 C Eb G B 1 b3 5 7 HarmMin, MelMin, DoHarMin C minor 6 Cm6 C-6 C Eb G A 1 b3 5 6 Dor, MelMin C minor 9 Cm9 C-9 C Eb G Bb D 1 b3 5 b7 9 Dor, Aeo, MinPent C diminished (triad) Cº Cdim C Eb Gb 1 b3 b5 Loc, Dim, ComDim, SupLoc C diminished 7 Cº7 Cdim7 C Eb Gb A(Bbb) 1 b3 b5 6(bb7) Dim C half diminished Cø -

Development of Musical Scales in Europe
RABINDRA BHARATI UNIVERSITY VOCAL MUSIC DEPARTMENT COURSE - B.A. ( Compulsory Course ) (CBCS) 2020 Semester - II , Paper - I Teacher - Sri Partha Pratim Bhowmik History of Western Music Development of musical scales in Europe In the 8th century B.C., The musical atmosphere of ancient Greece introduced its development by the influence of then popular aristocratic music. That music was melody- based and the root of that music was rural folk-songs. In each and every country, the development of music was rooted in the folk-songs. The European Aristocratic Music of the Christian Era had been inspired by the developed Greek music. In the 5th century B.C. the renowned Greek Mathematician Pythagoras had first established a relation between science and music. Before him, the scale of Greek music was pentatonic. Pythagoras changed the scale into hexatonic pattern and later into heptatonic pattern. Greek musicians applied the alphabets to indicate the notes of their music. For the natural notes they used the alphabets in normal position and for the deformed notes, the alphabets turned upside down [deformed notes= Vikrita svaras]. The musical instruments, they had invented are – Aulos, Salpinx, pan-pipes, harp, lyre, syrinx etc. In the western music, the term ‘scale’ is derived from Latin word ‘scala’, ie, the ladder; scale means an ascent or descent formation of the musical notes. Each and every scale has a starting note, called ‘tonic note’ [‘tone - tonic’ not the Health-Tonic]. In the Ancient Greece, the musical scale had been formed with the help of lyre , a string instrument, having normally 5 or 6 or 7 strings. -

3 Manual Microtonal Organ Ruben Sverre Gjertsen 2013
3 Manual Microtonal Organ http://www.bek.no/~ruben/Research/Downloads/software.html Ruben Sverre Gjertsen 2013 An interface to existing software A motivation for creating this instrument has been an interest for gaining experience with a large range of intonation systems. This software instrument is built with Max 61, as an interface to the Fluidsynth object2. Fluidsynth offers possibilities for retuning soundfont banks (Sf2 format) to 12-tone or full-register tunings. Max 6 introduced the dictionary format, which has been useful for creating a tuning database in text format, as well as storing presets. This tuning database can naturally be expanded by users, if tunings are written in the syntax read by this instrument. The freely available Jeux organ soundfont3 has been used as a default soundfont, while any instrument in the sf2 format can be loaded. The organ interface The organ window 3 MIDI Keyboards This instrument contains 3 separate fluidsynth modules, named Manual 1-3. 3 keysliders can be played staccato by the mouse for testing, while the most musically sufficient option is performing from connected MIDI keyboards. Available inputs will be automatically recognized and can be selected from the menus. To keep some of the manuals silent, select the bottom alternative "to 2ManualMicroORGANircamSpat 1", which will not receive MIDI signal, unless another program (for instance Sibelius) is sending them. A separate menu can be used to select a foot trigger. The red toggle must be pressed for this to be active. This has been tested with Behringer FCB1010 triggers. Other devices could possibly require adjustments to the patch. -

The Hungarian Rhapsodies and the 15 Hungarian Peasant Songs: Historical and Ideological Parallels Between Liszt and Bartók David Hill
James Madison University JMU Scholarly Commons Dissertations The Graduate School Spring 2015 The unH garian Rhapsodies and the 15 Hungarian Peasant Songs: Historical and ideological parallels between Liszt and Bartók David B. Hill James Madison University Follow this and additional works at: https://commons.lib.jmu.edu/diss201019 Part of the Musicology Commons Recommended Citation Hill, David B., "The unH garian Rhapsodies and the 15 Hungarian Peasant Songs: Historical and ideological parallels between Liszt and Bartók" (2015). Dissertations. 38. https://commons.lib.jmu.edu/diss201019/38 This Dissertation is brought to you for free and open access by the The Graduate School at JMU Scholarly Commons. It has been accepted for inclusion in Dissertations by an authorized administrator of JMU Scholarly Commons. For more information, please contact [email protected]. The Hungarian Rhapsodies and the 15 Hungarian Peasant Songs: Historical and Ideological Parallels Between Liszt and Bartók David Hill A document submitted to the graduate faculty of JAMES MADISON UNIVERSITY In Partial Fulfillment of the Requirements for the degree of Doctor of Musical Arts School of Music May 2015 ! TABLE!OF!CONTENTS! ! Figures…………………………………………………………………………………………………………….…iii! ! Abstract……………………………………………………………………………………………………………...iv! ! Introduction………………………………………………………………………………………………………...1! ! PART!I:!SIMILARITIES!SHARED!BY!THE!TWO!NATIONLISTIC!COMPOSERS! ! A.!Origins…………………………………………………………………………………………………………….4! ! B.!Ties!to!Hungary…………………………………………………………………………………………...…..9! -

Nora-Louise Müller the Bohlen-Pierce Clarinet An
Nora-Louise Müller The Bohlen-Pierce Clarinet An Introduction to Acoustics and Playing Technique The Bohlen-Pierce scale was discovered in the 1970s and 1980s by Heinz Bohlen and John R. Pierce respectively. Due to a lack of instruments which were able to play the scale, hardly any compositions in Bohlen-Pierce could be found in the past. Just a few composers who work in electronic music used the scale – until the Canadian woodwind maker Stephen Fox created a Bohlen-Pierce clarinet, instigated by Georg Hajdu, professor of multimedia composition at Hochschule für Musik und Theater Hamburg. Hence the number of Bohlen- Pierce compositions using the new instrument is increasing constantly. This article gives a short introduction to the characteristics of the Bohlen-Pierce scale and an overview about Bohlen-Pierce clarinets and their playing technique. The Bohlen-Pierce scale Unlike the scales of most tone systems, it is not the octave that forms the repeating frame of the Bohlen-Pierce scale, but the perfect twelfth (octave plus fifth), dividing it into 13 steps, according to various mathematical considerations. The result is an alternative harmonic system that opens new possibilities to contemporary and future music. Acoustically speaking, the octave's frequency ratio 1:2 is replaced by the ratio 1:3 in the Bohlen-Pierce scale, making the perfect twelfth an analogy to the octave. This interval is defined as the point of reference to which the scale aligns. The perfect twelfth, or as Pierce named it, the tritave (due to the 1:3 ratio) is achieved with 13 tone steps. -

Day 17 AP Music Handout, Scale Degress.Mus
Scale Degrees, Chord Quality, & Roman Numeral Analysis There are a total of seven scale degrees in both major and minor scales. Each of these degrees has a name which you are required to memorize tonight. 1 2 3 4 5 6 7 1 & w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic A triad can be built upon each scale degree. w w w w & w w w w w w w w 1. tonicw 2.w supertonic 3.w mediant 4. subdominant 5. dominant 6. submediant 7. leading tone 1. tonic The quality and scale degree of the triads is shown by Roman numerals. Captial numerals are used to indicate major triads with lowercase numerals used to show minor triads. Diminished triads are lowercase with a "degree" ( °) symbol following and augmented triads are capital followed by a "plus" ( +) symbol. Roman numerals written for a major key look as follows: w w w w & w w w w w w w w CM: wI (M) iiw (m) wiii (m) IV (M) V (M) vi (m) vii° (dim) I (M) EVERY MAJOR KEY FOLLOWS THE PATTERN ABOVE FOR ITS ROMAN NUMERALS! Because the seventh scale degree in a natural minor scale is a whole step below tonic instead of a half step, the name is changed to subtonic, rather than leading tone. Leading tone ALWAYS indicates a half step below tonic. Notice the change in the qualities and therefore Roman numerals when in the natural minor scale. -

Practical Music Theory – Book 1 by Pete Ford Table of Contents
Practical Music Theory – Book 1 by Pete Ford Table of Contents Preface xi About This Book Series xii To the Instructor xii Acknowledgements xii Part One Chapter 1: Notation 1 Clefs 1 The Grand Staff 2 Notes 2 Rests 3 Note Names 4 Rhythm 5 Simple Time 6 Dotted Notes in Simple Time 7 Compound Time 8 Subdivision in Compound Time 10 The Phrase Marking, Slur and the Tie 12 The Tie in Simple Time 12 The Tie in Compound Time 13 Repeat Signs, da Capo, and More 14 Assignment 1-1: Name the Notes 19 Assignment 1-2: Simple Time 21 Assignment 1-3: Compound Time 23 Chapter 2: Key Signatures 25 Writing Accidental Signs 25 The Cycle of Fourths 26 Key Signatures with Flats 27 Key Signatures with Sharps 28 Enharmonic Keys 30 Assignment 2-1: Name the Key Signature 33 Assignment 2-2: Key Signatures 35 Table of Contents Chapter 3: Building Scales 37 Writing the Major Scale 38 Introduction to Solfege 39 The Relative Minor Scale 40 The Cycle with Minor Keys Added 41 Writing the Natural Minor Scale 41 Solfege in Minor Keys 42 The Harmonic Minor Scale 44 The Melodic Minor Scale 46 Assignment 3-1: Write the Scales #1 49 Assignment 3-2: Write the Scales #2 51 Chapter 4: Intervals 53 Primary Intervals of the Major Scale 53 Writing Ascending Intervals 55 Writing Descending Intervals 57 Playing Intervals on the Piano 59 Hearing and Singing Intervals 59 Secondary Intervals 60 Writing Descending Secondary Intervals 62 Assignment 4-1: Write the Intervals 65 Assignment 4-2: Secondary Intervals 67 Part Two Chapter 5: Building Chords (SATB) 71 Triads of the Major Scale -

Harmonic Resources in 1980S Hard Rock and Heavy Metal Music
HARMONIC RESOURCES IN 1980S HARD ROCK AND HEAVY METAL MUSIC A thesis submitted to the College of the Arts of Kent State University in partial fulfillment of the requirements for the degree of Master of Arts in Music Theory by Erin M. Vaughn December, 2015 Thesis written by Erin M. Vaughn B.M., The University of Akron, 2003 M.A., Kent State University, 2015 Approved by ____________________________________________ Richard O. Devore, Thesis Advisor ____________________________________________ Ralph Lorenz, Director, School of Music _____________________________________________ John R. Crawford-Spinelli, Dean, College of the Arts ii Table of Contents LIST OF FIGURES ............................................................................................................................... v CHAPTER I........................................................................................................................................ 1 INTRODUCTION ........................................................................................................................... 1 GOALS AND METHODS ................................................................................................................ 3 REVIEW OF RELATED LITERATURE............................................................................................... 5 CHAPTER II..................................................................................................................................... 36 ANALYSIS OF “MASTER OF PUPPETS” ...................................................................................... -

Major and Minor Scales Half and Whole Steps
Dr. Barbara Murphy University of Tennessee School of Music MAJOR AND MINOR SCALES HALF AND WHOLE STEPS: half-step - two keys (and therefore notes/pitches) that are adjacent on the piano keyboard whole-step - two keys (and therefore notes/pitches) that have another key in between chromatic half-step -- a half step written as two of the same note with different accidentals (e.g., F-F#) diatonic half-step -- a half step that uses two different note names (e.g., F#-G) chromatic half step diatonic half step SCALES: A scale is a stepwise arrangement of notes/pitches contained within an octave. Major and minor scales contain seven notes or scale degrees. A scale degree is designated by an Arabic numeral with a cap (^) which indicate the position of the note within the scale. Each scale degree has a name and solfege syllable: SCALE DEGREE NAME SOLFEGE 1 tonic do 2 supertonic re 3 mediant mi 4 subdominant fa 5 dominant sol 6 submediant la 7 leading tone ti MAJOR SCALES: A major scale is a scale that has half steps (H) between scale degrees 3-4 and 7-8 and whole steps between all other pairs of notes. 1 2 3 4 5 6 7 8 W W H W W W H TETRACHORDS: A tetrachord is a group of four notes in a scale. There are two tetrachords in the major scale, each with the same order half- and whole-steps (W-W-H). Therefore, a tetrachord consisting of W-W-H can be the top tetrachord or the bottom tetrachord of a major scale. -

Helmholtz's Dissonance Curve
Tuning and Timbre: A Perceptual Synthesis Bill Sethares IDEA: Exploit psychoacoustic studies on the perception of consonance and dissonance. The talk begins by showing how to build a device that can measure the “sensory” consonance and/or dissonance of a sound in its musical context. Such a “dissonance meter” has implications in music theory, in synthesizer design, in the con- struction of musical scales and tunings, and in the design of musical instruments. ...the legacy of Helmholtz continues... 1 Some Observations. Why do we tune our instruments the way we do? Some tunings are easier to play in than others. Some timbres work well in certain scales, but not in others. What makes a sound easy in 19-tet but hard in 10-tet? “The timbre of an instrument strongly affects what tuning and scale sound best on that instrument.” – W. Carlos 2 What are Tuning and Timbre? 196 384 589 amplitude 787 magnitude sample: 0 10000 20000 30000 0 1000 2000 3000 4000 time: 0 0.23 0.45 0.68 frequency in Hz Tuning = pitch of the fundamental (in this case 196 Hz) Timbre involves (a) pattern of overtones (Helmholtz) (b) temporal features 3 Some intervals “harmonious” and others “discordant.” Why? X X X X 1.06:1 2:1 X X X X 1.89:1 3:2 X X X X 1.414:1 4:3 4 Theory #1:(Pythagoras ) Humans naturally like the sound of intervals de- fined by small integer ratios. small ratios imply short period of repetition short = simple = sweet Theory #2:(Helmholtz ) Partials of a sound that are close in frequency cause beats that are perceived as “roughness” or dissonance. -

When the Leading Tone Doesn't Lead: Musical Qualia in Context
When the Leading Tone Doesn't Lead: Musical Qualia in Context Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Claire Arthur, B.Mus., M.A. Graduate Program in Music The Ohio State University 2016 Dissertation Committee: David Huron, Advisor David Clampitt Anna Gawboy c Copyright by Claire Arthur 2016 Abstract An empirical investigation is made of musical qualia in context. Specifically, scale-degree qualia are evaluated in relation to a local harmonic context, and rhythm qualia are evaluated in relation to a metrical context. After reviewing some of the philosophical background on qualia, and briefly reviewing some theories of musical qualia, three studies are presented. The first builds on Huron's (2006) theory of statistical or implicit learning and melodic probability as significant contributors to musical qualia. Prior statistical models of melodic expectation have focused on the distribution of pitches in melodies, or on their first-order likelihoods as predictors of melodic continuation. Since most Western music is non-monophonic, this first study investigates whether melodic probabilities are altered when the underlying harmonic accompaniment is taken into consideration. This project was carried out by building and analyzing a corpus of classical music containing harmonic analyses. Analysis of the data found that harmony was a significant predictor of scale-degree continuation. In addition, two experiments were carried out to test the perceptual effects of context on musical qualia. In the first experiment participants rated the perceived qualia of individual scale-degrees following various common four-chord progressions that each ended with a different harmony. -

HOW to FIND RELATIVE MINOR and MAJOR SCALES Relative
HOW TO FIND RELATIVE MINOR AND MAJOR SCALES Relative minor and major scales share all the same notes–each one just has a different tonic. The best example of this is the relative relationship between C-major and A-minor. These two scales have a relative relationship and therefore share all the same notes. C-major: C D E F G A B C A-minor: A B C D E F G A Finding the relative minor from a known major scale (using the 6th scale degree) scale degrees: 1 2 3 4 5 6 7 1 C-major: C D E F G A B C A-(natural) minor: A B C D E F G A A-minor starts on the 6th scale degree of C-major. This relationship holds true for ALL major and minor scale relative relationships. To find the relative minor scale from a given major scale, count up six scale degrees in the major scale–that is where the relative minor scale begins. This minor scale will be the natural minor mode. 1 2 3 4 5 6 C-D-E-F-G-A The relative minor scale can also be found by counting backwards (down) by three scale degrees in the major scale. C-major: C D E F G A B C ←←← count DOWN three scale degrees and arrive at A 1 2 3 C-B-A Finding the relative major from a known minor scale (using the 3rd scale degree) scale degrees: 1 2 3 4 5 6 7 1 A-(natural) minor: A B C D E F G A C-major: C D E F G A B C C-major starts on the 3rd scale of A-minor.