Prediction of Final Football League Standings by Dynamic Frontier Estimation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Live Live Live
LIVE LIVE LIVE 27.08. 12:00 Canada North Korea 27.08. 16:00 Macclesfield Barrow ... 27.08. 16:00 FC Pakhtakor PFC Shurtan 27.08. 16:00 Billericay Town AFC Hornchurch 27.08. 16:00 Gateshead FC Lincoln City 27.08. 16:00 Rotor Volgograd Ural Ekaterinburg ... 27.08. 16:00 Tamworth FC Wrexham FC 27.08. 16:00 Ebbsfleet Utd Luton Town 27.08. 16:00 Bromley FC Tonbridge 27.08. 17:00 Hapoel Ashkelon Maccabi Petach 27.08. 17:00 Martic, Petra Stosur, Samantha Eurosport 27.08. 17:00 Lacko, Lukas Blake, James Eurosport 27.08. 17:00 Cirstea, Sorana Lisicki, Sabine Eurosport 27.08. 17:00 Bartoli, Marion Hampton, Jamie 27.08. 17:00 FC Salyut FK Yenisey 27.08. 17:00 Hapoel Nazrat Beitar Tel Aviv 27.08. 17:30 FC Honka Vaasa PS 27.08. 17:30 FC Kuban Volga Nizhny 27.08. 18:00 Ceahlaul Piatra FC Viitorul 27.08. 18:00 FC Baltika FC Ufa 27.08. 18:00 Jablonec Sparta Praha CT 4 27.08. 18:00 FC Universitatea FC Brasov 27.08. 18:15 Sock, Jack Mayer, Florian 27.08. 18:15 Mathieu, Paul- Andreev, Igor 1 of 6 27.08. 18:20 Oudin, Melanie Safarova, Lucie 27.08. 18:30 PFC Oleksandria Gelios Kharkiv 27.08. 18:30 MKS Pogon KS Lechia Gdansk 27.08. 18:35 Latvia Romania Digi Sport 2 27.08. 19:00 IFK Varnamo Trelleborgs FF 27.08. 19:00 AC Horsens AGF Aarhus 27.08. 19:00 Mjallby AIF Syrianska FC 27.08. 19:00 Karsiyaka Manisaspor 27.08. -

Profesyonel Futbolcu Sözleşmelerinin İnsan Kaynakları Muhasebesi Açısından Değerlemesi” Olup, Dört Ana Bölümden Oluşmaktadır
T.C İstanbul Üniversitesi Sosyal Bilimler Enstitüsü İşletme Anabilim Dalı Muhasebe Bilim Dalı Yüksek Lisans Tezi PROFESYONEL FUTBOLCU SÖZLEŞMELERİNİN İNSAN KAYNAKLARI MUHASEBESİ AÇISINDAN DEĞERLEMESİ Mustafa Günaydın 2501900039 Tez Danışmanı Prof. Dr. Fatih YILMAZ İstanbul-2019 ÖZ PROFESYONEL FUTBOLCU SÖZLEŞMELERİNİN İNSAN KAYNAKLARI MUHASEBESİ AÇISINDAN DEĞERLEMESİ Mustafa GÜNAYDIN Profesyonel Futbolcu Sözleşmelerinin, İnsan Kaynakları Muhasebesi açısından değerlemesi oldukça karmaşık bir süreçtir. Bugüne kadar İnsan Kaynakları Muhasebesi konusunda geliştirilen hiçbir etkili yasal düzenleme (Muhasebe Standardı/Vergi Yasaları) bulunmamaktadır. İnsan Kaynakları Muhasebesi, insan sermayesine yapılan yatırım maliyetlerini kârı azaltan giderler olarak değerlendiren geleneksel muhasebesinin aksine, insan kaynakları ile ilgili harcamaların varlık olarak hesaplanmasını içerir. Türkiye’de “Gençlik ve Spor Genel Müdürlüğü ile özerk spor federasyonlarına tescil edilmiş spor kulüplerinin idman ve spor faaliyetlerinde bulunan iktisadî işletmeleri ile sadece idman ve spor faaliyetlerinde bulunan anonim şirketler” kurumlar vergisinden muaf oldukları için uygulanan muhasebe sistemleri özensizdir. Günümüzde, dernek statüsünde kurulan futbol kulüplerinin kullandığı yöntemler ile borsada işlem gören futbol şirketleri arasında maddi olmayan duran varlıkların kullanım alanları arasında net bir ayrım olduğunu görüyoruz. Bu bilgiden elde edilebilecek tek şey, futbol kulüpleri arasında futbolcu sözleşmelerinin muhasebeleştirilmesi konusunda uyum olmadığı ve -

Bir Arada Işine Başladı
12-1:Layout 1 11.06.2018 21:21 Page 2 Grandmedical Manisaspor’da MANiSASPOR’DA dün saat 14.00’da BÜYÜKŞEHİR’İN DEVLERİ Esnaf Sanatkarlar Kredi Kefalet Ko- YENi BAŞKAN operatifi Sosyal POTADA YENİDEN ZİRVEDE Tesislerinde yapılan kongre sonrası yeni BÜLENT başkan belli oldu. 816 üyesi olan -80 Manisaspor’da, 95 BAYGELDİ kongreye 386 üye katılarak oy kul- landı. 386 oyun 4’ü geçersiz olurken, 382 oy geçerli sayıldı. C Manisaspor’un yeni başkanı oldu. Gökay Budak ise 190 oy aldı.SAYFA 11 İMSAK 03:49 İFTAR 20:40 Türkiye Erkekler Basketbol 2. Ligi’nde final grubunda Gemlik Basketbol takımıyla Atatürk Spor Salonu’nda karşı karşıya gelen Manisa Büyükşehir Belediyespor’un dev adamları salondan 95-80 galip ayrılarak hedefe büyük ölçüde ulaştı ve yeniden liderlik koltuğunu kaptı. Son periyoddaki performansı ile rakibini mağlup etmeyi başaran Manisa Büyükşehir’in dev adamları Türkiye Bas- ketbol Ligi’ne çıkmayı büyük ölçüde garantiledi.SAYFA 12 11 HAZİRAN 2018 PAZARTESİ YIL:8 SAYI:2435 FİYATI:50 KURUŞ KAVSAGA TAM NOT Manisa Büyükşehir Belediyesi tarafından Turgutlu’da eski kavşağının yerine yapılan Turgutlu Katlı Kavşak Projesi’nin 1. etabı Manisa Büyükşehir Belediye Başkanı Cengiz Ergün tarafından açılmıştı. Kavşağı kullanan vatandaşların büyük beğenisini kazanan kavşaktan geçiş yapan MHP Genel Başkanı Devlet Bahçeli, modern kavşağa tam not verdi. “TURGUTLU’YA CAN VERİYORUZ” Akçay’dan seçim çıkartması Kavşağı kullananlar arasında İzmir’de Bölge İstişare Toplantısı’na 24 Haziran seçim çalışmaları kapsamında Kırkağaç’a katılan MHP Genel Başkanı Devlet Bahçeli de yer aldı. Manisa giden MHP Grup Başkanvekili Erkan AKÇAY “Biz vatan ve millet sevdalısıyız. Siyasetin rüzgârına göre yelkeni- Büyükşehir Belediyesinin Turgutlu’da önemli bir hizmeti hayata mizi çevirmeyiz. -
![Taraftarium24!!!]***Sivasspor - Beşiktaş Canlı İzle Maçı Yayını 17-08-2019 Süper Lig Bein Sports 1 HD](https://docslib.b-cdn.net/cover/0142/taraftarium24-sivasspor-be%C5%9Fikta%C5%9F-canl%C4%B1-izle-ma%C3%A7%C4%B1-yay%C4%B1n%C4%B1-17-08-2019-s%C3%BCper-lig-bein-sports-1-hd-170142.webp)
Taraftarium24!!!]***Sivasspor - Beşiktaş Canlı İzle Maçı Yayını 17-08-2019 Süper Lig Bein Sports 1 HD
~*[(((Taraftarium24!!!]***Sivasspor - Beşiktaş Canlı İzle Maçı Yayını 17-08-2019 Süper Lig beIN Sports 1 HD Sivasspor - Beşiktaş Maçı Canlı Anlatım Olarak İzle - Spor Haberleri Sivasspor - Beşiktaş maçını canlı olarak Stadyum'dan takip edebilirsiniz. İşte Sivasspor - Beşiktaş maçının canlı anlatımı ve maça dair son istatistikler... Sivasspor Beşiktaş Maçı Canlı Izle Haberleri - Son Dakika Yeni ... Sivasspor Beşiktaş Maçı Canlı Izle haberi sayfasında en son yaşanan sivasspor beşiktaş maçı canlı izle gelişmeleri ile birlikte geçmişten bugüne CNN Türk'e ... En çok okunan haberler Canlı Maç İzle. Tüm spor karşılaşmalarını, şifreli tüm spor kanallarını JestBahis farkıyla ücretsiz olarak hd kalitede canlı maç izlemek için JestYayın.com'u tercih ... Sivasspor - Beşiktaş maçı canlı anlatım - Maç özeti, son dakika ... - Sporx Tarih: 18 Ağustos 2019 Pazar 03:00. Lig: Süper Lig. Sivasspor -. Beşiktaş ... MAÇ İSTATİSTİĞİ. KARŞILAŞTIRMA. Bu maça ait canlı anlatım bulunmamaktadır. Sivasspor Beşiktaş GOLLERİ İZLE, Beşiktaş Sivasspor maçı tüm ... 22 Nis 2019 - Sivasspor Beşiktaş maçı özet ve golleri izle!Beşiktaş, Spor Toto Süper Lig'in 29. haftasında deplasmanda Demir Grup Sivasspor ile karşılaştı. ++BJK++Besiktas.,Sivasspor,.Macini,.izle - Read the Docs Demir Grup Sivasspor-Beşiktaş - Sabah canlı skor. ... 19.08.2018 | Büyükşehir Belediye Erzurumspor - Beşiktaş 19.08.2018 | Akhisarspor - Çaykur Rizespor Sivasspor Beşiktaş Süper Lig maçı ne zaman, saat kaçta? - Son ... 1 gün önce - Beşiktaş Süper Lig ilk hafta mücadelesi kapsamında Sivasspor deplasmanına konuk oluyor. Kadrosuna kattığı yeni isimlerle sezona hızlı bir ... Sivasspor Beşiktaş maçı ne zaman? Sivasspor BJK maçı saat kaçta ... 1 gün önce - Sivasspor Beşiktaş maçı ne zaman saat kaçta sorusu siyah beyazlı ... Beşiktaş da sezonun ilk haftasında Sivaspor deplasmanında 3 puan ... Sivasspor Beşiktaş maçı ne zaman? - Yeni Şafak 2 gün önce - Demir Grup Sivasspor, Süper Lig'in ilk haftasında 17 Ağustos Cumartesi günü sahasında Beşiktaş ile yapacağı karşılaşmanın hazırlıklarını .. -
![JUSTIN-TV!!!] Beşiktaş - Denizlispor Canlı Izle Maçı Yayını 10-11-2019 Süper Lig Bein Sports 1 HD Linkler](https://docslib.b-cdn.net/cover/3771/justin-tv-be%C5%9Fikta%C5%9F-denizlispor-canl%C4%B1-izle-ma%C3%A7%C4%B1-yay%C4%B1n%C4%B1-10-11-2019-s%C3%BCper-lig-bein-sports-1-hd-linkler-183771.webp)
JUSTIN-TV!!!] Beşiktaş - Denizlispor Canlı Izle Maçı Yayını 10-11-2019 Süper Lig Bein Sports 1 HD Linkler
~*[(((JUSTIN-TV!!!] Beşiktaş - Denizlispor canlı izle maçı yayını 10-11-2019 Süper Lig beIN Sports 1 HD Linkler LİG TV: Beşiktaş - Denizlispor maçını canlı izle 10 Kasım 2019 ((bEİN TV!!))@*Beşiktaş - Denizlispor maçını canlı izle 10 Kasım 2019...Beşiktaş Denizlispor canlı skor, video yayını ve H2H sonuçları ... Beşiktaş Denizlispor canlı maçı skor (ve video çevrimiçi canlı izle yayın) 10.11.2019. tarihte 16:00 satte (UTC ile) Vodafone Park stadyumu, Istanbul, Turkey ... Beşiktaş - Denizlispor maçı canlı anlatım - Maç özeti, son ... Hakem: Özgür Yankaya. Beşiktaş -. Denizlispor -. GOLLER & KARTLAR ... MAÇ İSTATİSTİĞİ. KARŞILAŞTIRMA. Bu maça ait canlı anlatım bulunmamaktadır. Beşiktaş - Denizlispor maçı goller ve kartlar - Maç özeti, son ... CANLI ANLATIM · İSTATİSTİK · YORUMLAR. Beşiktaş. Denizlispor. Kayserispor Fenerbahçe maçı özet ve golleri izle (bein sports) · Antalyaspor Beşiktaş maçı ... Beşiktaş - Denizlispor maçı ne zaman, saat kaçta, hangi ... 13 saat önce - Beşiktaş - Denizlispor maçı ne zaman, saat kaçta, hangi kanalda? Süper Lig'de Beşiktaş 11. haftasında maçında Yukatel Denizlispor ile karşı ... ı bilet fiyatları… Beşiktaş ... DRT Denizli & Denizli Gazetesi Beşiktaş - Yukatel Denizlispor maçı canlı izle (10.11.2019) 2 gün önce - Beşiktaş Yukatel Denizlispor maçının hangi kanalda yayınlanacağı karşılaşmayı takip etmek isteyen futbolseverler tarafından araştırılmaya ... 10.11.2019 Beşiktaş vs Denizlispor maçı Hangi Kanalda Saat ... 1 gün önce - 10.11.2019 Beşiktaş vs Denizlispor maçı hangi kanalda saat kaçta yayınlanacak? Beşiktaş - Denizlispor maçı ne zaman, saat kaçta, hangi kanalda? Süper Lig'de Beşiktaş 11. haftasında maçında Yukatel Denizlispor ile karşı ... ı bilet fiyatları… Beşiktaş ... DRT Denizli & Denizli Gazetesi Beşiktaş - Yukatel Denizlispor maçı canlı izle (10.11.2019) 2 gün önce - Beşiktaş Yukatel Denizlispor maçının hangi kanalda yayınlanacağı karşılaşmayı takip etmek isteyen futbolseverler tarafından araştırılmaya .. -

Profesyonel Müsabakalar Amatör Müsabakalar
TÜRKİYE FUTBOL FEDERASYONU İSTANBUL İL TEMSİLCİLİĞİ SAYI : 2019-20-27 04.03.2020 KONU : HAFTALIK MÜSABAKA PROGRAMI HK. SAYIN; SPOR KULÜBÜ BAŞKANLIĞI, FUTBOL HAKEMİ, SAHA KOMİSERİ VE SAĞLIK GÖREVLİSİ; İLİMİZDE 02.03.2020 – 12.03.2020 TARİHLERİNDE OYNANACAK OLAN MÜSABAKA PROGRAMLARI AŞAĞIYA ÇIKARILMIŞTIR. BİLGİLERİNİZİ RİCA EDERİM. ALİ M.TANRIYAŞÜKÜR TFF İSTANBUL İL TEMSİLCİSİ PROFESYONEL MÜSABAKALAR 02 Mart 2020 Pazartesi BAŞAKŞEHİR FATİH TERİM STADI 20:00 MEDİPOL BAŞAKŞEHİR FK - GAZİANTEP FUTBOL KLB.AŞ. Süper Lig HASAN DURAN 06 Mart 2020 Cuma VODAFONE PARK 20:00 BEŞİKTAŞ A.Ş. - MKE ANKARAGÜCÜ Süper Lig ERDEM RİZELİ 07 Mart 2020 Cumartesi BAYRAMPAŞA ÇETİN EMEÇ STADI 14:30 BAYRAMPAŞA - DARICA G.BİRLİĞİ TFF 3.LİG FAHRİ AŞICI VEFA STADI 16:30 FATİH KARAGÜMRÜK - ADANADEMİRSPOR TFF 1.Lig ZAFER ÇATALKAYA ALEMDAĞ STADYUMU 14:30 1877 ALEMDAĞ - ESENLER EROKSPOR TFF 3.LİG AYHAN KENARCI SANCAKTEPE 15 TEMMUZ STADI SANCAKTEPE FUTBOL KULÜBÜ A.Ş. - YILPORT 14:30 TFF 2.Lig CEMAL SİVRİKAYA SAMSUNSPOR ŞİLE STADI 14:30 ŞİLESPOR - ÇATALCASPOR TFF 3.LİG MURAT DOĞAN ÜLKER STADYUMU FENERBAHÇE ŞÜKRÜ SARAÇOĞLU SPOR KOMPLEKSİ 20:00 FENERBAHÇE A.Ş. - DENİZLİSPOR Süper Lig 08 Mart 2020 Pazar SİLİVRİ STADI 14:30 SİLİVRİSPOR - TOKATSPOR TFF 3.LİG ORHAN UĞUN TEPECİK ŞENOL GÜNEŞ STADI 14:30 BÜYÜKÇEKMECE TEPECİKSPOR - PAYASSPOR TFF 3.LİG ÖZGÜR KORKMAZ BAKIRKÖY BELEDİYE 1 NOLU SAHA 14:00 YEŞİLKÖY - BEYOĞLU YENİÇARŞI Spor Toto BAL ÖNDER DENLİ EYÜP STADI 13:30 EYÜPSPOR - SİVAS BLD. TFF 2.Lig ALİ ÖZTÜRK EV SAH. SEYIRCISIZ İBB BAYRAMPAŞA STADI 14:00 BEŞYÜZEVLER - ÇİĞLİ BLD. Spor Toto BAL BURHAN KAHVECİ İBB CEBECİ SPOR KOMPLEKSİ 14:00 SULTANGAZİ - BAĞCILAR SPOR Spor Toto BAL KEMAL SAKAOĞLU RECEP TAYYİP ERDOĞAN STADI 13:30 KASIMPAŞA A.Ş. -
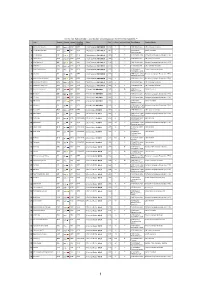
The-KA-Club-Rating-2Q-2021 / June 30, 2021 the KA the Kick Algorithms ™
the-KA-Club-Rating-2Q-2021 / June 30, 2021 www.kickalgor.com the KA the Kick Algorithms ™ Club Country Country League Conf/Fed Class Coef +/- Place up/down Class Zone/Region Country Cluster Continent ⦿ 1 Manchester City FC ENG ENG � ENG UEFA 1 High Supreme ★★★★★★ 1,928 +1 UEFA British Isles UK / overseas territories ⦿ 2 FC Bayern München GER GER � GER UEFA 1 High Supreme ★★★★★★ 1,907 -1 UEFA Central DACH Countries Western Europe ≡ ⦿ 3 FC Barcelona ESP ESP � ESP UEFA 1 High Supreme ★★★★★★ 1,854 UEFA Iberian Zone Romance Languages Europe (excl. FRA) ⦿ 4 Liverpool FC ENG ENG � ENG UEFA 1 High Supreme ★★★★★★ 1,845 +1 UEFA British Isles UK / overseas territories ⦿ 5 Real Madrid CF ESP ESP � ESP UEFA 1 High Supreme ★★★★★★ 1,786 -1 UEFA Iberian Zone Romance Languages Europe (excl. FRA) ⦿ 6 Chelsea FC ENG ENG � ENG UEFA 1 High Supreme ★★★★★★ 1,752 +4 UEFA British Isles UK / overseas territories ≡ ⦿ 7 Paris Saint-Germain FRA FRA � FRA UEFA 1 High Supreme ★★★★★★ 1,750 UEFA Western France / overseas territories Continental Europe ⦿ 8 Juventus ITA ITA � ITA UEFA 1 High Supreme ★★★★★★ 1,749 -2 UEFA Central / East Romance Languages Europe (excl. FRA) Mediterranean Zone ⦿ 9 Club Atlético de Madrid ESP ESP � ESP UEFA 1 High Supreme ★★★★★★ 1,676 -1 UEFA Iberian Zone Romance Languages Europe (excl. FRA) ⦿ 10 Manchester United FC ENG ENG � ENG UEFA 1 High Supreme ★★★★★★ 1,643 +1 UEFA British Isles UK / overseas territories ⦿ 11 Tottenham Hotspur FC ENG ENG � ENG UEFA 1 High Supreme ★★★★★★ 1,628 -2 UEFA British Isles UK / overseas territories ≡ ⬇ 12 Borussia Dortmund GER GER � GER UEFA 2 Primary High ★★★★★ 1,541 UEFA Central DACH Countries Western Europe ≡ ⦿ 13 Sevilla FC ESP ESP � ESP UEFA 2 Primary High ★★★★★ 1,531 UEFA Iberian Zone Romance Languages Europe (excl. -

Uefa Europa League
UEFA EUROPA LEAGUE - 2017/18 SEASON MATCH PRESS KITS Konya Büyükşehir Belediyesi Stadyumu - Konya Thursday 28 September 2017 Konyaspor 19.00CET (20.00 local time) Vitória SC Group I - Matchday 2 Last updated 26/09/2017 12:06CET Fixtures and results 2 Legend 5 1 Konyaspor - Vitória SC Thursday 28 September 2017 - 19.00CET (20.00 local time) Match press kit Konya Büyükşehir Belediyesi Stadyumu, Konya Fixtures and results Konyaspor Date Competition Opponent Result Goalscorers 13/08/2017 League Trabzonspor AŞ (A) L 1-2 Fofana 2 21/08/2017 League Gençlerbirliği SK (H) W 3-0 Araz 24, 53, Skubic 43 27/08/2017 League İstanbul Başakşehir (A) L 1-2 Skubic 88 09/09/2017 League Alanyaspor (H) L 0-2 14/09/2017 UEL Olympique de Marseille (A) L 0-1 18/09/2017 League Beşiktaş JK (A) L 0-2 23/09/2017 League Akhisar Belediyespor (H) W 2-0 Ömer Ali Şahiner 17, Friday 73 28/09/2017 UEL Vitória SC (H) 01/10/2017 League Yeni Malatyaspor (A) 14/10/2017 League Galatasaray AŞ (H) 19/10/2017 UEL FC Salzburg (H) 22/10/2017 League Kayserispor (A) 28/10/2017 League Osmanlıspor (H) 02/11/2017 UEL FC Salzburg (A) 05/11/2017 League Sivasspor (A) 18/11/2017 League Antalyaspor (H) 23/11/2017 UEL Olympique de Marseille (H) 26/11/2017 League Kasımpaşa SK (A) 03/12/2017 League Bursaspor (H) 07/12/2017 UEL Vitória SC (A) 11/12/2017 League Kardemir Karabükspor (H) 18/12/2017 League Göztepe Izmir (A) 23/12/2017 League Fenerbahçe SK (H) 21/01/2018 League Trabzonspor AŞ (H) 28/01/2018 League Gençlerbirliği SK (A) 04/02/2018 League İstanbul Başakşehir (H) 11/02/2018 League Alanyaspor -

Bereket Dergisi 2009
Çoğu Gitti Azı Kaldı WBazıal- Manalistlerart, Wa iyimserliğinlt Dis ney, Bbuo iaşamadang ve S henüzony 'n in de erkenara olduğunu la rýn da b söyleyipu lun du ð dahau 18 kötünün viz yo n egeleceğinir þir ke tin 'ÖZ'ü söyleseko ru yde,up ,olumlu ge liþ m sinyallerie yi sü rek de li t egörmezdenþ vik ede re kge re- ka bet - lemeyiz.çi ol d Temeluk la rý nekonomiký vur gu lu ygöstergeleror. henüz kriz öncesineDe dönmese ði þim, y ede ni lenen mazındane gi b i durağanlaşmışza man iþi dir ve bu ve küçük de olsa yönünü yukarı çevirmiş durum- sü re cin usu lü ne uy gun ola rak yö ne til me si ge re - da. Tüketici güven endeksinin de tüm dünyada yenidenkir. E yükselişðer de ð itrendine þim, ye ngirdiğii len m edikkat sü re cçekiyor.i iyi yö ne til - Bu mkrizinez i sdee ibirþ le güven rin da eksikliğinden ha kö tü ye gi tderinleştiğinime ris ki de b u lun - gözm önüneak ta d ýralırsak. Di ðe ryada bir ialdığımızfad ey le Dtaktirde,im yat'a artanpi rin ce gi - tüketicider k egüveninen ev de ki bakarak,bul gur d a‘Çoğun ol m agitti;k da azıvar .kal- dı’ diyebiliriz. Öte yandan uzmanlar, insanların yaşadığıK enu r uderinm s aacılarınl de ð bilei þi m 9 iay-birn gö syıl te içinr ge- si de küllendiğini belirtiyorlar. Daha önce yaşanan Fahrettin Yahþi 'ÖZ'ü kay bet me den de ði þim açý sýn dan bak tý - Fahrettin Yahşi krizlerin de 9 ay-bir yıl ömürlü olduğunu dikkate aldığımızda,ðý mýz za m‘Çoğuan he gitti;m s eazık tö kaldı’ rel he demeninm de ku rerkenum sa l ola- iyimserlikrak ba þolmayacağınıa rý lý bir sü re cdüşünüyoruz.i ge ri de bý ra kBu tý ð duyguý mý zý söy le - ve ydüşüncelerlee bi li riz. -

The Open Sore of Football: Aggressive Violent Behavior and Hooliganism
PHYSICAL CULTURE AND SPORT. STUDIES AND RESEARCH DOI: 10.1515/pcssr-2016-0015 The Open Sore of Football: Aggressive Violent Behavior and Hooliganism Authors’ contribution: Osman GumusgulA,C,D, Mehmet AcetB,E A) conception and design of the study B) acquisition of data Dumlupinar University, Turkey C) analysis and interpretation of data D) manuscript preparation E) obtaining funding ABSTRACT Aggression and violence have been a customary part of life that mankind has had to live with from the beginning of time; it has been accepted by society even though it expresses endless negativity. Aggression and violence can find a place in sports events and football games because of the social problems of the audience watching the competitions or games, which sometimes fall into the category of hooliganism. Turkey is one of the countries that should consider this problem to be a serious social problem. Even during 2014 and 2015, a relatively short period of time, there were significant hazardous acts committed by hooligans. In February 2014, one supporter was killed after a game between Liverpool and Arsenal in England; in March 2014, a game between Trabzonspor and Fenerbahce was left half-finished because of violent acts in the stadium that caused players in the pitch to believe that they could not leave stadium alive, although they finally left after a few hours; in another incident in March 2014, one supporter was killed after a game between Helsingborg and Djugarden in Sweden; in November 2014, one supporter was killed and 14 supporters were injured before the game between Atletico Madrid and Deportivo in Spain. -

Footballers with Migration Background in the German National Football Team
“It is about the flag on your chest!” Footballers with Migration Background in the German National Football Team. A matter of inclusion? An Explorative Case Study on Nationalism, Integration and National Identity. Oscar Brito Capon Master Thesis in Sociology Department of Sociology and Human Geography Faculty of Social Sciences University of Oslo June 2012 Oscar Brito Capon - Master Thesis in Sociology 2 Oscar Brito Capon - Master Thesis in Sociology Foreword Dear reader, the present research work represents, on one hand, my dearest wish to contribute to the understanding of some of the effects that the exclusionary, ethnocentric notions of nationhood and national belonging – which have characterized much of western European thinking throughout history – have had on individuals who do not fit within the preconceived frames of national unity and belonging with which most Europeans have been operating since the foundation of the nation-state approximately 140 years ago. On the other hand, this research also represents my personal journey to understand better my role as a citizen, a man, a father and a husband, while covered by a given aura of otherness, always reminding me of my permanent foreignness in the country I decided to make my home. In this sense, this has been a personal journey to learn how to cope with my new ascribed identity as an alien (my ‘labelled forehead’) without losing my essence in the process, and without forgetting who I also am and have been. This journey has been long and tough in many forms, for which I would like to thank the help I have received from those who have been accompanying my steps all along. -

A M Y O R U Z A
KURTULUŞ SAVAŞIMIZIN KA RANLIK KALMIŞ BtR YANINA OKUL SÖZLÜKLERİ IŞIK TUTAN KİTAP Tl,. İNGİLİZ KAYNAKLARINDAN ALMANCATtİRKÇE Okul Soıltiitl 10,— ALMANCA-TÜRKÇI Cep Soritijflı 7.50 ALMANCA-TÜRKÇK Deyimler Siizliiilı 7.50 TÜRK KURMUŞ İNGlUZCE-TtİRKÇE Okul SnrUlftiı 12 50 tNGtLtZCE-TÜRKÇL Cep Sözlüiii 7.50 FRANSIZCA-TÜRKÇE Okul Lügati 12.50 FRANSIZCA-TÜRKÇF Cep SHelüJU 7.50 SAVASI NOT: Söktükler Türkçe telâffuzudur. Yazan: TANER BAYTOK OKUL SİPARİŞLERİ İFA EDİLİR. Fiyatı: 26 TL. KtTAFÇILARDA BULUNUR. ÖDEMELİ Dağıtım: GE-DA Genel Dağıttın GÖNDERİLİR. Cağaloğlu/tSTANBÜL Sipariş Merkezi î Cumhuriyet — 11140 47. yıl, sayı: 16629 Telgraf ve mektup adresi: Cumhuriyet İstanbul - Posta Kutusu: İstanbul No- 24« ÖÖRETİM YAYINEVİ: Ankara Cad. «2-2 Telefonlar: 22 42 90 — 22 42 Si, — 22 42 97 — 22 42 98 — 22 42 99 10 Kasım Salı 1970 İSTANBUL ACI A T n 10 Yİ AMYORUZ ANKARA - K U Ş L A R — (ÇmnJums et fîuı »mi ; Bir özgür ülke arıyorlardı, bir özgür çiçek, Göçü güzeldi kuşların. Dağ mı, orman mı, ova mı ha Aziz Atatürk, ölümünün 32. Günü aydınlıkla gün edecek. yıldönümünde bugün bütün yurtta törenlerle anılacaktır. Kanatlan var da Anma törenleri sabahleyin Atatürk’ün ebediyete intikal Yoktu yurtları, ettiği saat olan 09.05 te Anıt Kirlenmemiş buğdayı ararlarken kabirde başlıyacak, diğer il Hicaz arkalarda kaldı, Irak, Ürdün arkalarda ve ilçelerde de ayni saatte yapılacaktır. Amt-kabirde ya pılacak anma törenine Cum Güneşle kar hurbaşkanı ile askeri, mül Birbirine kanşsm isterlerdi, ki erkân, meslek kuruluşları, Gagalarında yaşamak dernekler katılacaklar, bun Bir ısıya değil bir varoluşa acıkmıştılar. lar saat 8.40 ta Arslanlı yo lun başlangıcında hazır bu lunacaklardır.