DOCSLIB.ORG

Lecture Slides

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture Slides Outline Meta-Classes Guy Wiener Introduction AOP Classes Generation 1 Introduction Meta-Classes in Python Logging 2 Meta-Classes in Python Delegation Meta-Classes vs. Traditional OOP 3 Meta-Classes vs. Traditional OOP Outline Meta-Classes Guy Wiener Introduction AOP Classes Generation 1 Introduction Meta-Classes in Python Logging 2 Meta-Classes in Python Delegation Meta-Classes vs. Traditional OOP 3 Meta-Classes vs. Traditional OOP What is Meta-Programming? Meta-Classes Definition Guy Wiener Meta-Program A program that: Introduction AOP Classes One of its inputs is a program Generation (possibly itself) Meta-Classes in Python Its output is a program Logging Delegation Meta-Classes vs. Traditional OOP Meta-Programs Nowadays Meta-Classes Guy Wiener Introduction AOP Classes Generation Compilers Meta-Classes in Python Code Generators Logging Delegation Model-Driven Development Meta-Classes vs. Traditional Templates OOP Syntactic macros (Lisp-like) Meta-Classes The Problem With Static Programming Meta-Classes Guy Wiener Introduction AOP Classes Generation Meta-Classes How to share features between classes and class hierarchies? in Python Logging Share static attributes Delegation Meta-Classes Force classes to adhere to the same protocol vs. Traditional OOP Share code between similar methods Meta-Classes Meta-Classes Guy Wiener Introduction AOP Classes Definition Generation Meta-Classes in Python Meta-Class A class that creates classes Logging Delegation Objects that are instances of the same class Meta-Classes share the same behavior vs. Traditional OOP Classes that are instances of the same meta-class share the same behavior Meta-Classes Meta-Classes Guy Wiener Introduction AOP Classes Definition Generation Meta-Classes in Python Meta-Class A class that creates classes Logging Delegation Objects that are instances of the same class Meta-Classes share the same behavior vs. Traditional OOP Classes that are instances of the same meta-class share the same behavior Classes create objects ⇒ Meta-classes create classes Aspect-Oriented Programming (AOP) Meta-Classes Guy Wiener A meta-programming methodology based on OOP Introduction Goal: Make all methods that match a pattern adhere to AOP Classes the same behavior (called “ advice ”) Generation Meta-Classes in Python Logging Examples Delegation Meta-Classes vs. Traditional Print logging OOP Perform a security check Ask for permission . Aspect-Oriented Programming (AOP) Meta-Classes Guy Wiener A meta-programming methodology based on OOP Introduction Goal: Make all methods that match a pattern adhere to AOP Classes the same behavior (called “ advice ”) Generation Meta-Classes in Python Logging Examples Delegation Meta-Classes vs. Traditional Print logging OOP Perform a security check Ask for permission . Function decorators are not enough We want to enforce a policy. AOP Example Meta-Classes Guy Wiener Advice Code Introduction AOP if (!connected) class Client { Classes Generation connect(); void send(server) { Meta-Classes in Python // send message Logging Delegation } Meta-Classes void receive(server) { vs. Traditional OOP // receive message } } AOP Example Meta-Classes Guy Wiener Advice Code Introduction AOP if (!connected) class Client { Classes Generation connect(); void send(server) { Meta-Classes in Python if (!connected) Logging Delegation connect(); Meta-Classes // send message vs. Traditional OOP } void receive(server) { if (!connected) connect(); // receive message } } AOP Programs Meta-Classes Guy Wiener Introduction AOP Components of an AOP meta-program Classes Generation Meta-Classes in Python Advices Shared code Logging Delegation Patterns Which advice applies to which points in the code Meta-Classes (entry or exit of a method) vs. Traditional OOP AOP Programs Meta-Classes Guy Wiener Introduction AOP Components of an AOP meta-program Classes Generation Meta-Classes in Python Advices Shared code Logging Delegation Patterns Which advice applies to which points in the code Meta-Classes (entry or exit of a method) vs. Traditional OOP Input A program and specifications Output A new program Applying an AOP program on a Program Meta-Classes A generic meta-class for AOP Guy Wiener Introduction Input: class C, advice a, pattern p AOP Output: class C, modified Classes Generation for method m ∈ methods( C) do Meta-Classes in Python if m matches p then Logging Delegation m’ = apply a on m Meta-Classes replace m with m’ in C vs. Traditional OOP end if end for Applying an AOP program on a Program Meta-Classes A generic meta-class for AOP Guy Wiener Introduction Input: class C, advice a, pattern p AOP Output: class C, modified Classes Generation for method m ∈ methods( C) do Meta-Classes in Python if m matches p then Logging Delegation m’ = apply a on m Meta-Classes replace m with m’ in C vs. Traditional OOP end if end for Requires: Reflection Modification AOP Example Meta-Classes Guy Wiener Introduction AOP An aspect for connecting to a server Classes Generation for method m ∈ Client do Meta-Classes in Python if m has an argument server then Logging Delegation insert Meta-Classes if (!connected) vs. Traditional “ OOP connect();” before m end if end for The RMI Problem Meta-Classes Remove Method Invocation (RMI) Guy Wiener Introduction A server object is located on one computer AOP Classes Clients invokes methods of the server object from other Generation Meta-Classes computers in Python Logging Delegation Meta-Classes vs. Traditional start() OOP stop() Server Object pause(5) Figure: Remote Method Invocation RMI Class Diagram Meta-Classes Guy Wiener ServerInf Introduction AOP start()* Classes Generation stop()* pause(int)* Meta-Classes in Python Server Logging Delegation start() Meta-Classes stop() vs. Traditional pause(int) OOP Server+ Figure: The original Server start()+ class stop()+ pause(int)+ Figure: Server class and interface RMI Class Diagram (cont’d) Meta-Classes Guy Wiener ServerInf Introduction AOP start()* Classes Generation stop()* pause(int)* Meta-Classes in Python Logging Delegation Meta-Classes vs. Traditional Stub+ Skeleton+ ServerImpl+ OOP over start()+ start()+ start()+ stop()+ network stop()+ stop()+ pause(int)+ pause(int)+ pause(int)+ Figure: Server with stub and skeleton RMI Classes Generation Meta-Classes Guy Wiener ServerInf Introduction start()* AOP stop()* Classes pause(int)* Generation Meta-Classes Generated Classes: in Python Logging Delegation Input: Meta-Classes Code Generator vs. Traditional Server interface OOP Output: Skeleton Stub Stub+ Skeleton+ start()+ start()+ stop()+ stop()+ pause(int)+ pause(int)+ Figure: Classes generation for RMI Object-Oriented Code Generation Meta-Classes Guy Wiener Input Class definitions Introduction AOP Classes Interfaces, IDL Generation UML Meta-Classes in Python Other specifications Logging Delegation Output Generated classes Meta-Classes vs. Traditional Stubs and skeletons OOP Persistent objects Database tables . Object-Oriented Code Generation Meta-Classes Guy Wiener Input Class definitions Introduction AOP Classes Interfaces, IDL Generation UML Meta-Classes in Python Other specifications Logging Delegation Output Generated classes Meta-Classes vs. Traditional Stubs and skeletons OOP Persistent objects Database tables . The structure of the program becomes the source for automatically generated code Outline Meta-Classes Guy Wiener Introduction AOP Classes Generation 1 Introduction Meta-Classes in Python Logging 2 Meta-Classes in Python Delegation Meta-Classes vs. Traditional OOP 3 Meta-Classes vs. Traditional OOP Motivation Meta-Classes Guy Wiener Problem Introduction AOP Classes Generation Python’s flexibility makes the code impossible to Meta-Classes understand in Python Logging A more organized mechanism is required Delegation Meta-Classes vs. Traditional OOP Motivation Meta-Classes Guy Wiener Problem Introduction AOP Classes Generation Python’s flexibility makes the code impossible to Meta-Classes understand in Python Logging A more organized mechanism is required Delegation Meta-Classes vs. Traditional OOP The OOP Solution Class in Python are objects Objects are instances of classes Motivation Meta-Classes Guy Wiener Problem Introduction AOP Classes Generation Python’s flexibility makes the code impossible to Meta-Classes understand in Python Logging A more organized mechanism is required Delegation Meta-Classes vs. Traditional OOP The OOP Solution Class in Python are objects Objects are instances of classes Classes are instances of Meta-Classes Meta-Classes in Python Meta-Classes Guy Wiener Introduction AOP Classes Generation Meta-Classes Meta-Classes in Python Logging Extend the type “ type” Delegation Meta-Classes Responsible for creating new classes vs. Traditional OOP The dynamic members of the meta-class become static members of the instance class Creating Classes from Meta-Classes Meta-Classes Example Guy Wiener Introduction AOP # Meta-Class Classes Generation class Printable(type): Meta-Classes def whoami(self): print "I am ", self.__name__ in Python Logging Delegation Meta-Classes >>> Foo = Printable(’Foo’,(),{}) # Empty new class vs. Traditional OOP >>> Foo.whoami() I am Foo >>> Foo.__class__ <class ’Printable’> >>> f = Foo() # Object >>> f.__class__ <class ’Foo’> The metaclass field Meta-Classes Guy Wiener Introduction AOP Classes Generation Class C is an instance of a meta-class M if: Meta-Classes in Python 1 Logging C has a static field metaclass Delegation 2 One of the ancestors classes of C is an instance of M Meta-Classes vs. Traditional OOP 3 There is a global variable metaclass 4 Otherwise, the default meta-class
Load more

Recommended publications
  • 1=Haskell =1=Making Our Own Types and Typeclasses
    Haskell Making Our Own Types and Typeclasses http://igm.univ-mlv.fr/~vialette/?section=teaching St´ephaneVialette LIGM, Universit´eParis-Est Marne-la-Vall´ee November 13, 2016 Making Our Own Types and Typeclasses Algebraic data types intro So far, we've run into a lot of data types: Bool, Int, Char, Maybe, etc. But how do we make our own? One way is to use the data keyword to define a type. Let's see how the Bool type is defined in the standard library. data Bool= False| True data means that we're defining a new data type. Making Our Own Types and Typeclasses Algebraic data types intro data Bool= False| True The part before the = denotes the type, which is Bool. The parts after the = are value constructors. They specify the different values that this type can have. The | is read as or. So we can read this as: the Bool type can have a value of True or False. Both the type name and the value constructors have to be capital cased. Making Our Own Types and Typeclasses Algebraic data types intro We can think of the Int type as being defined like this: data Int=-2147483648|-2147483647| ...|-1|0|1|2| ...| 2147483647 The first and last value constructors are the minimum and maximum possible values of Int. It's not actually defined like this, the ellipses are here because we omitted a heapload of numbers, so this is just for illustrative purposes. Shape let's think about how we would represent a shape in Haskell.
    [Show full text]
  • A Polymorphic Type System for Extensible Records and Variants
    A Polymorphic Typ e System for Extensible Records and Variants Benedict R. Gaster and Mark P. Jones Technical rep ort NOTTCS-TR-96-3, November 1996 Department of Computer Science, University of Nottingham, University Park, Nottingham NG7 2RD, England. fbrg,[email protected] Abstract b oard, and another indicating a mouse click at a par- ticular p oint on the screen: Records and variants provide exible ways to construct Event = Char + Point : datatyp es, but the restrictions imp osed by practical typ e systems can prevent them from b eing used in ex- These de nitions are adequate, but they are not par- ible ways. These limitations are often the result of con- ticularly easy to work with in practice. For example, it cerns ab out eciency or typ e inference, or of the di- is easy to confuse datatyp e comp onents when they are culty in providing accurate typ es for key op erations. accessed by their p osition within a pro duct or sum, and This pap er describ es a new typ e system that reme- programs written in this way can b e hard to maintain. dies these problems: it supp orts extensible records and To avoid these problems, many programming lan- variants, with a full complement of p olymorphic op era- guages allow the comp onents of pro ducts, and the al- tions on each; and it o ers an e ective type inference al- ternatives of sums, to b e identi ed using names drawn gorithm and a simple compilation metho d.
    [Show full text]
  • Typescript Language Specification
    TypeScript Language Specification Version 1.8 January, 2016 Microsoft is making this Specification available under the Open Web Foundation Final Specification Agreement Version 1.0 ("OWF 1.0") as of October 1, 2012. The OWF 1.0 is available at http://www.openwebfoundation.org/legal/the-owf-1-0-agreements/owfa-1-0. TypeScript is a trademark of Microsoft Corporation. Table of Contents 1 Introduction ................................................................................................................................................................................... 1 1.1 Ambient Declarations ..................................................................................................................................................... 3 1.2 Function Types .................................................................................................................................................................. 3 1.3 Object Types ...................................................................................................................................................................... 4 1.4 Structural Subtyping ....................................................................................................................................................... 6 1.5 Contextual Typing ............................................................................................................................................................ 7 1.6 Classes .................................................................................................................................................................................
    [Show full text]
  • A System of Constructor Classes: Overloading and Implicit Higher-Order Polymorphism
    A system of constructor classes: overloading and implicit higher-order polymorphism Mark P. Jones Yale University, Department of Computer Science, P.O. Box 2158 Yale Station, New Haven, CT 06520-2158. [email protected] Abstract range of other data types, as illustrated by the following examples: This paper describes a flexible type system which combines overloading and higher-order polymorphism in an implicitly data Tree a = Leaf a | Tree a :ˆ: Tree a typed language using a system of constructor classes – a mapTree :: (a → b) → (Tree a → Tree b) natural generalization of type classes in Haskell. mapTree f (Leaf x) = Leaf (f x) We present a wide range of examples which demonstrate mapTree f (l :ˆ: r) = mapTree f l :ˆ: mapTree f r the usefulness of such a system. In particular, we show how data Opt a = Just a | Nothing constructor classes can be used to support the use of monads mapOpt :: (a → b) → (Opt a → Opt b) in a functional language. mapOpt f (Just x) = Just (f x) The underlying type system permits higher-order polymor- mapOpt f Nothing = Nothing phism but retains many of many of the attractive features that have made the use of Hindley/Milner type systems so Each of these functions has a similar type to that of the popular. In particular, there is an effective algorithm which original map and also satisfies the functor laws given above. can be used to calculate principal types without the need for With this in mind, it seems a shame that we have to use explicit type or kind annotations.
    [Show full text]
  • Python Programming
    Python Programming Wikibooks.org June 22, 2012 On the 28th of April 2012 the contents of the English as well as German Wikibooks and Wikipedia projects were licensed under Creative Commons Attribution-ShareAlike 3.0 Unported license. An URI to this license is given in the list of figures on page 149. If this document is a derived work from the contents of one of these projects and the content was still licensed by the project under this license at the time of derivation this document has to be licensed under the same, a similar or a compatible license, as stated in section 4b of the license. The list of contributors is included in chapter Contributors on page 143. The licenses GPL, LGPL and GFDL are included in chapter Licenses on page 153, since this book and/or parts of it may or may not be licensed under one or more of these licenses, and thus require inclusion of these licenses. The licenses of the figures are given in the list of figures on page 149. This PDF was generated by the LATEX typesetting software. The LATEX source code is included as an attachment (source.7z.txt) in this PDF file. To extract the source from the PDF file, we recommend the use of http://www.pdflabs.com/tools/pdftk-the-pdf-toolkit/ utility or clicking the paper clip attachment symbol on the lower left of your PDF Viewer, selecting Save Attachment. After extracting it from the PDF file you have to rename it to source.7z. To uncompress the resulting archive we recommend the use of http://www.7-zip.org/.
    [Show full text]
  • Refinement Types for ML
    Refinement Types for ML Tim Freeman Frank Pfenning [email protected] [email protected] School of Computer Science School of Computer Science Carnegie Mellon University Carnegie Mellon University Pittsburgh, Pennsylvania 15213-3890 Pittsburgh, Pennsylvania 15213-3890 Abstract tended to the full Standard ML language. To see the opportunity to improve ML’s type system, We describe a refinement of ML’s type system allow- consider the following function which returns the last ing the specification of recursively defined subtypes of cons cell in a list: user-defined datatypes. The resulting system of refine- ment types preserves desirable properties of ML such as datatype α list = nil | cons of α * α list decidability of type inference, while at the same time fun lastcons (last as cons(hd,nil)) = last allowing more errors to be detected at compile-time. | lastcons (cons(hd,tl)) = lastcons tl The type system combines abstract interpretation with We know that this function will be undefined when ideas from the intersection type discipline, but remains called on an empty list, so we would like to obtain a closely tied to ML in that refinement types are given type error at compile-time when lastcons is called with only to programs which are already well-typed in ML. an argument of nil. Using refinement types this can be achieved, thus preventing runtime errors which could be 1 Introduction caught at compile-time. Similarly, we would like to be able to write code such as Standard ML [MTH90] is a practical programming lan- case lastcons y of guage with higher-order functions, polymorphic types, cons(x,nil) => print x and a well-developed module system.
    [Show full text]
  • Java Secrets.Pdf
    Java Secrets by Elliotte Rusty Harold IDG Books, IDG Books Worldwide, Inc. ISBN: 0764580078 Pub Date: 05/01/97 Buy It Preface About the Author Part I—How Java Works Chapter 1—Introducing Java SECRETS A Little Knowledge Can Be a Dangerous Thing What’s in This Book? Part I: How Java Works Part II: The sun Classes Part III: Platform-Dependent Java Why Java Secrets? Broader applicability More power Inspiration Where Did the Secrets Come From? Where is the documentation? The source code The API documentation What Versions of Java Are Covered? Some Objections Java is supposed to be platform independent Why aren’t these things documented? FUD (fear, uncertainty, and doubt) How secret is this, anyway? Summary Chapter 2—Primitive Data Types Bytes in Memory Variables, Values, and Identifiers Place-Value Number Systems Binary notation Hexadecimal notation Octal notation Integers ints Long, short, and byte Floating-Point Numbers Representing floating-point numbers in binary code Special values Denormalized floating-point numbers CHAR ASCII ISO Latin-1 Unicode UTF8 Boolean Cross-Platform Issues Byte order Unsigned integers Integer widths Conversions and Casting Using a cast The mechanics of conversion Bit-Level Operators Some terminology Bitwise operators Bit shift operators Summary Chapter 2—Primitive Data Types Bytes in Memory Variables, Values, and Identifiers Place-Value Number Systems Binary notation Hexadecimal notation Octal notation Integers ints Long, short, and byte Floating-Point Numbers Representing floating-point numbers in binary code
    [Show full text]
  • Haskell-Style Type Classes with Isabelle/Isar
    Isar ∀ Isabelle= α λ β → Haskell-style type classes with Isabelle/Isar Florian Haftmann 20 February 2021 Abstract This tutorial introduces Isar type classes, which are a convenient mech- anism for organizing specifications. Essentially, they combine an op- erational aspect (in the manner of Haskell) with a logical aspect, both managed uniformly. 1 INTRODUCTION 1 1 Introduction Type classes were introduced by Wadler and Blott [8] into the Haskell lan- guage to allow for a reasonable implementation of overloading1. As a canon- ical example, a polymorphic equality function eq :: α ) α ) bool which is overloaded on different types for α, which is achieved by splitting introduc- tion of the eq function from its overloaded definitions by means of class and instance declarations: 2 class eq where eq :: α ) α ) bool instance nat :: eq where eq 0 0 = True eq 0 - = False eq - 0 = False eq (Suc n)(Suc m) = eq n m instance (α::eq; β::eq) pair :: eq where eq (x1; y1) (x2; y2) = eq x1 x2 ^ eq y1 y2 class ord extends eq where less-eq :: α ) α ) bool less :: α ) α ) bool Type variables are annotated with (finitely many) classes; these annotations are assertions that a particular polymorphic type provides definitions for overloaded functions. Indeed, type classes not only allow for simple overloading but form a generic calculus, an instance of order-sorted algebra [5, 6, 10]. From a software engineering point of view, type classes roughly correspond to interfaces in object-oriented languages like Java; so, it is naturally desirable that type classes do not only provide functions (class parameters) but also state specifications implementations must obey.
    [Show full text]
  • OMG Meta Object Facility (MOF) Core Specification
    Date : October 2019 OMG Meta Object Facility (MOF) Core Specification Version 2.5.1 OMG Document Number: formal/2019-10-01 Standard document URL: https://www.omg.org/spec/MOF/2.5.1 Normative Machine-Readable Files: https://www.omg.org/spec/MOF/20131001/MOF.xmi Informative Machine-Readable Files: https://www.omg.org/spec/MOF/20131001/CMOFConstraints.ocl https://www.omg.org/spec/MOF/20131001/EMOFConstraints.ocl Copyright © 2003, Adaptive Copyright © 2003, Ceira Technologies, Inc. Copyright © 2003, Compuware Corporation Copyright © 2003, Data Access Technologies, Inc. Copyright © 2003, DSTC Copyright © 2003, Gentleware Copyright © 2003, Hewlett-Packard Copyright © 2003, International Business Machines Copyright © 2003, IONA Copyright © 2003, MetaMatrix Copyright © 2015, Object Management Group Copyright © 2003, Softeam Copyright © 2003, SUN Copyright © 2003, Telelogic AB Copyright © 2003, Unisys USE OF SPECIFICATION - TERMS, CONDITIONS & NOTICES The material in this document details an Object Management Group specification in accordance with the terms, conditions and notices set forth below. This document does not represent a commitment to implement any portion of this specification in any company's products. The information contained in this document is subject to change without notice. LICENSES The companies listed above have granted to the Object Management Group, Inc. (OMG) a nonexclusive, royalty-free, paid up, worldwide license to copy and distribute this document and to modify this document and distribute copies of the modified version. Each of the copyright holders listed above has agreed that no person shall be deemed to have infringed the copyright in the included material of any such copyright holder by reason of having used the specification set forth herein or having conformed any computer software to the specification.
    [Show full text]
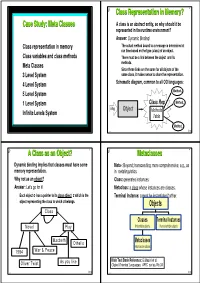
  • Metaclasses 4 ◆ Dynamic Binding Implies That Classes Must Have Some ◆ Meta-: Beyond; Transcending; More Comprehensive; E.G., As Memory Representation
    ® 1 ® Class Representation in Memory? 2 Case Study: Meta Classes ◆ A class is an abstract entity, so why should it be represented in the runtime environment? ◆ Answer: Dynamic Binding! ◆ Class representation in memory ● The actual method bound to a message is determined at run time based on the type (class) of an object. ◆ Class variables and class methods ● There must be a link between the object and its ◆ Meta Classes methods. ● Since these links are the same for all objects of the ◆ 3 Level System same class, it makes sense to share the representation. ◆ ◆ 4 Level System Schematic diagram, common to all OO languages: Method ◆ 5 Level System 1 Method ◆ 1 Level System Class Rep 2 ◆ Msg Object Methods Infinite Levels System Table Methodn oop Õ Ö oop Õ Ö ® A Class as an Object? 3 ® Metaclasses 4 ◆ Dynamic binding implies that classes must have some ◆ Meta-: Beyond; transcending; more comprehensive; e.g., as memory representation. in metalinguistics. ◆ Why not as an object? ◆ Class: generates instances. ◆ Answer: Let's go for it! ◆ Metaclass: a class whose instances are classes. ● Each object o has a pointer to its class object c which is the ◆ Terminal Instance: cannot be instantiated further. object representing the class to which o belongs. Objects Class Classes Terminal Instances Novel Play Instantiable objects Non instantiable objects Macbeth Othello Metaclasses Instances are classes 1984 War & Peace As you like Main Text Book Reference: G.Masini et al. Oliver Twist Object-Oriented Languages, APIC series, No.34 oop Õ Ö oop Õ Ö ® 5 ® 6 Taxonomy of Metaclass Systems The 3 Level System ◆ 1-Level System: Objects only Object ● Each object describes itself INSTANCE _OF ● No need for classes: objects are ìinstantiatedî or ìinheritedî from SUBCLASS _OF other objects Class Example: Self VARIABLES instance_of ,167$1&(B2) ◆ 2-Level System: Objects, Classes METHODS ..
    [Show full text]
  • Marshmallow-Annotations Documentation Release 2.4.1
    marshmallow-annotations Documentation Release 2.4.1 Alec Nikolas Reiter Jan 28, 2021 Contents 1 Installation 3 2 Content 5 Index 21 i ii marshmallow-annotations Documentation, Release 2.4.1 Version 2.4.1 (Change Log) marshmallow-annotations allows you to create marshmallow schema from classes with annotations on them: # music.py from typing import List class Album: id: int name: str def __init__(self, id: int, name: str): self.id= id self.name= name class Artist: id: int name: str albums: List[Album] def __init__(self, id: int, name: str, albums: List[Album]): self.id= id self.name= name self.albums= albums # schema.py from marshmallow_annotations import AnnotationSchema from.music import Album, Artist class AlbumScheme(AnnotationSchema): class Meta: target= Album register_as_scheme= True class ArtistScheme(AnnotationSchema): class Meta: target= Artist register_as_scheme= True scheme= ArtistScheme() scheme.dump( Artist( id=1, name="Abominable Putridity", albums=[ Album( id=1, name="The Anomalies of Artificial Origin" ) ] ) ) #{ # "albums": [ #{ # "id": 1, (continues on next page) Contents 1 marshmallow-annotations Documentation, Release 2.4.1 (continued from previous page) # "name": "The Anomalies of Artificial Origin" #} # ], # "id": 1, # "name": "Abominable Putridity" #} 2 Contents CHAPTER 1 Installation marshmallow-annotations is available on pypi and installable with: pip install marshmallow-annotations marshmallow-annotations supports Python 3.6+ and marshmallow 2.x.x Note: If you are install marshmallow-annotations outside of a virtual environment, consider installing with pip install --user marshmallow-annotations rather than using sudo or adminstrator privileges to avoid installing it into your system Python. 3 marshmallow-annotations Documentation, Release 2.4.1 4 Chapter 1. Installation CHAPTER 2 Content 2.1 Quickstart This guide will walk you through the basics of using marshmallow-annotations.
    [Show full text]
  • Java Class Types 12 September
    CSCI 136: Fall 2018 Handout 3 Java Class Types 12 September Class Types We noted earlier that the String type in Java was not a primitive (or array) type. It is what Java calls a class- based (or class) type—this is the third category of types in Java. Class types, are based on class declarations. Class declarations allow us to create objects that can hold more complex collections of data, along with operations for accessing/modifying that data. For example public class Student { private int age; private String name; private char grade; public Student(int theAge, String theName, char theGrade) { age = theAge; name = theName; grade = theGrade; } public int getAge() { return age;} public String getName() { return name;} public char getGrade() { return grade;} public void setAge(int newAge) { age = newAge;} public void setGrade(char grade) { this.grade = grade;} } The above, grotesquely oversimplified, class declaration specifies the data components (instance variables) of a Stu- dent object, along with a method (called a constructor∗) describing how to create such objects, and several short methods for accessing/modifying the data components (fields/instance variables) of a Student object. Given such a class declaration, one can write programs that declare (and create) variables of type Student: Student a; Student b; a = new Student(18, "Patti Smith", ’A’); b = new Student(20, "Joan Jett", ’B’); Or, combining the declaration of the variables and creation (instantiation) of the corresponding values (objects): Student a = new Student(18, "Patti Smith", ’A’); Student b = new Student(20, "Joan Jett", ’B’); The words public and private are called access level modifiers; they control the extent to which other classes can create, access, or modify objects, their fields, and their methods.
    [Show full text]