DOCSLIB.ORG

A Polymorphic Type System for Extensible Records and Variants

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Polymorphic Type System for Extensible Records and Variants A Polymorphic Typ e System for Extensible Records and Variants Benedict R. Gaster and Mark P. Jones Technical rep ort NOTTCS-TR-96-3, November 1996 Department of Computer Science, University of Nottingham, University Park, Nottingham NG7 2RD, England. fbrg,[email protected] Abstract b oard, and another indicating a mouse click at a par- ticular p oint on the screen: Records and variants provide exible ways to construct Event = Char + Point : datatyp es, but the restrictions imp osed by practical typ e systems can prevent them from b eing used in ex- These de nitions are adequate, but they are not par- ible ways. These limitations are often the result of con- ticularly easy to work with in practice. For example, it cerns ab out eciency or typ e inference, or of the di- is easy to confuse datatyp e comp onents when they are culty in providing accurate typ es for key op erations. accessed by their p osition within a pro duct or sum, and This pap er describ es a new typ e system that reme- programs written in this way can b e hard to maintain. dies these problems: it supp orts extensible records and To avoid these problems, many programming lan- variants, with a full complement of p olymorphic op era- guages allow the comp onents of pro ducts, and the al- tions on each; and it o ers an e ective type inference al- ternatives of sums, to b e identi ed using names drawn gorithm and a simple compilation metho d. It is a prac- from some given set of labels. Lab elled pro ducts are tical system that can b e understo o d and implemented more commonly known as records or structs, while la- as a natural extension of languages like Standard ML b elled sums are p erhaps b etter known as variants or and Haskell. In an area that has already received a unions. For example, the Date and Event datatyp es great deal of attention from the research community, describ ed ab ove might b e de ned more attractively as: the typ e system describ ed here is the rst to combine all of these features in a practical framework. Date = Rec fjday :Int ; month : Int ; year :Int jg One imp ortant asp ect of this work is the emphasis Event = Var fjkey :Char ; mouse : Point jg: that it places on the use of rows in the construction of This notation captures a common feature in the con- record and variant typ es. As a result, with only small struction of record and variant types, using rows of the extensions of the core typ e system, we are able to intro- form fjl : ;:::; l : jg to describ e mappings that as- duce new, p owerful op erations on records using features 1 1 n n so ciate a type with each of the (distinct) lab els l . such as row p olymorphism and rst-class lab els. i i Record types are obtained by preceding rows with the symb ol Rec . Variant types are constructed using Var . 1 Intro duction For example, if r = fjl : ;:::; l : jg and e ,::: ,e have 1 1 n n 1 n types ,::: , , resp ectively, then we can form a record 1 n Pro ducts and sums play fundamental roles in the con- (l = e ;:::; l = e ) of type Rec r , or distinct vari- 1 1 n n struction of datatyp es: pro ducts describ e grouping of ants, hl = e i;:::; hl = e i, each of type Var r . Thus, 1 1 n n data items, while sums express choices b etween alter- 0 0 (day = 25; month = 12; year = 1996) and hkey = a i natives. For example, we might represent a date as a represent values of type Date and Event , resp ectively. pro duct, with three integer comp onents sp ecifying the day, month, and year: 1.1 Polymorphism and extensibility Date = Int Int Int : Unfortunately, practical languages are often less exi- ble in the op erations that they provide to manipulate For a simple example of a sum, consider the type of records and variants. For example, many languages| input events to a window system, with one alternative from C to Standard ML (SML)|will only allow the pro- indicating that a character has b een entered on the key- grammer to select the l comp onent, r :l , from a record r 1 selection op erator ( if the typ e of r is uniquely determined at compile-time . :l ) has type: These languages do not supp ort polymorphic op erations 8 :8r :Rec fjl : j r jg ! : on records|such as a general selector function ( :l ) that will extract a value from any record that has an l eld. However, the op erations and types in Wand's system A further weakness in many of these languages is that are unchecked; for example, extending a row with an l they provide no real supp ort for extensibility; there are eld may either add a completely new eld, or replace no general op erators for adding a eld, removing a eld, an existing eld lab elled with l . As a result, some pro- renaming a eld, or replacing a eld (p ossibly with a grams do not have principal types [27]. value of a di erent typ e) in a record value. There have b een many previous attempts to design Flags: Remy has developed a exible treatment for typ e systems for records and variants that supp ort p oly- extensible records and variants in a natural extension of morphism and extensibility. Such work is imp ortant, ML [23]. A key feature of his system is the use of ags not just in its own right, but also in its application to to enco de b oth p ositive and negative information|that the study of ob ject-oriented or database programming is, to indicate which elds must b e present, and which languages where these facilities seem particularly use- must b e absent. Again, a concept of row variables is ful. We will summarize the key features of some of these used to deal with other elds whose presence or absence earlier systems here b efore describing our own prop osal. is not signi cant in a particular situation. For example, the selection op erator has type: Subtyping: Subtyping is one of the most widely used techniques for building typ e systems for records and 8 :8r :Rec fjl : pre ( ) j r jg ! ; variants [3, 5, 4, 21]. We can de ne a subtyping relation by sp ecifying that a row r is a subrow of r , written 1 2 where pre ( ) is a ag indicating the presence of a eld r r , if r contains all the elds of r , and p ossibly 1 2 1 2 of type , and r is a row variable representing the rest more. The intuition here is that, for example, a record of the record. Intuitively, records in Remy's system of typ e Rec r could b e used in any context where a 1 are represented by tuples with a slot for each p ossible value of typ e Rec r is exp ected, and conversely, that a 2 lab el. The type system prevents access to unde ned variant of typ e Var r can b e substituted in any context 2 comp onents, but do es not lead directly to a simple and where a value of typ e Var r is required. In particular, 1 ecient implementation. :l ) can b e treated as a function the selection op erator ( of typ e: Predicates: Harp er and Pierce [8, 7] studied type 8 :8r fjl : jg:Rec r ! : systems for extensible records using predicates on types This op eration is implemented, at least conceptually, to capture information ab out presence or absence of by co ercing from Rec r to a known type|the singleton elds, and to restrict attention to checked op erations. Rec fjl : jg|and then extracting the required eld. One For example, writing r #r for the assertion that the 1 2 weakness of this approach is that information ab out the rows r and r have disjoint sets of lab els, the selection 1 2 other elds in the record is lost, so it is harder to de- op erator op erator ( :l ) has type: scrib e op erations like record extension. For example, 8 :8r :(r #fjl : jg) ) Rec (r k fjl : jg) ! ; observing that b ounded quanti cation is not by itself sucient, Cardelli and Mitchell [5] used an overriding where r k r is the row obtained by merging r and r , 1 2 1 2 op erator on typ es to overcome this problem. and is only de ned if r #r . Harp er and Pierce's work 1 2 do es not deal with variants, type inference, or compila- Row extension: Motivated by studies of ob ject- tion, and do es not provide an op erational interpretation oriented programming, Wand [26] intro duced the con- of predicates. However, their approach to record typing cept of row variables to allow incremental construction was one of the motivating examples in Jones' work on of record and variant typ es. For example, a record of quali ed types [11] where a general framework for type typ e Rec fjl : j r jg has all of the elds of a record of inference and compilation was developed, including a typ e Rec r , together with a eld l of type .
Load more

Recommended publications
  • 1=Haskell =1=Making Our Own Types and Typeclasses
    Haskell Making Our Own Types and Typeclasses http://igm.univ-mlv.fr/~vialette/?section=teaching St´ephaneVialette LIGM, Universit´eParis-Est Marne-la-Vall´ee November 13, 2016 Making Our Own Types and Typeclasses Algebraic data types intro So far, we've run into a lot of data types: Bool, Int, Char, Maybe, etc. But how do we make our own? One way is to use the data keyword to define a type. Let's see how the Bool type is defined in the standard library. data Bool= False| True data means that we're defining a new data type. Making Our Own Types and Typeclasses Algebraic data types intro data Bool= False| True The part before the = denotes the type, which is Bool. The parts after the = are value constructors. They specify the different values that this type can have. The | is read as or. So we can read this as: the Bool type can have a value of True or False. Both the type name and the value constructors have to be capital cased. Making Our Own Types and Typeclasses Algebraic data types intro We can think of the Int type as being defined like this: data Int=-2147483648|-2147483647| ...|-1|0|1|2| ...| 2147483647 The first and last value constructors are the minimum and maximum possible values of Int. It's not actually defined like this, the ellipses are here because we omitted a heapload of numbers, so this is just for illustrative purposes. Shape let's think about how we would represent a shape in Haskell.
    [Show full text]
  • Generic Programming
    Generic Programming July 21, 1998 A Dagstuhl Seminar on the topic of Generic Programming was held April 27– May 1, 1998, with forty seven participants from ten countries. During the meeting there were thirty seven lectures, a panel session, and several problem sessions. The outcomes of the meeting include • A collection of abstracts of the lectures, made publicly available via this booklet and a web site at http://www-ca.informatik.uni-tuebingen.de/dagstuhl/gpdag.html. • Plans for a proceedings volume of papers submitted after the seminar that present (possibly extended) discussions of the topics covered in the lectures, problem sessions, and the panel session. • A list of generic programming projects and open problems, which will be maintained publicly on the World Wide Web at http://www-ca.informatik.uni-tuebingen.de/people/musser/gp/pop/index.html http://www.cs.rpi.edu/˜musser/gp/pop/index.html. 1 Contents 1 Motivation 3 2 Standards Panel 4 3 Lectures 4 3.1 Foundations and Methodology Comparisons ........ 4 Fundamentals of Generic Programming.................. 4 Jim Dehnert and Alex Stepanov Automatic Program Specialization by Partial Evaluation........ 4 Robert Gl¨uck Evaluating Generic Programming in Practice............... 6 Mehdi Jazayeri Polytypic Programming........................... 6 Johan Jeuring Recasting Algorithms As Objects: AnAlternativetoIterators . 7 Murali Sitaraman Using Genericity to Improve OO Designs................. 8 Karsten Weihe Inheritance, Genericity, and Class Hierarchies.............. 8 Wolf Zimmermann 3.2 Programming Methodology ................... 9 Hierarchical Iterators and Algorithms................... 9 Matt Austern Generic Programming in C++: Matrix Case Study........... 9 Krzysztof Czarnecki Generative Programming: Beyond Generic Programming........ 10 Ulrich Eisenecker Generic Programming Using Adaptive and Aspect-Oriented Programming .
    [Show full text]
  • Java Secrets.Pdf
    Java Secrets by Elliotte Rusty Harold IDG Books, IDG Books Worldwide, Inc. ISBN: 0764580078 Pub Date: 05/01/97 Buy It Preface About the Author Part I—How Java Works Chapter 1—Introducing Java SECRETS A Little Knowledge Can Be a Dangerous Thing What’s in This Book? Part I: How Java Works Part II: The sun Classes Part III: Platform-Dependent Java Why Java Secrets? Broader applicability More power Inspiration Where Did the Secrets Come From? Where is the documentation? The source code The API documentation What Versions of Java Are Covered? Some Objections Java is supposed to be platform independent Why aren’t these things documented? FUD (fear, uncertainty, and doubt) How secret is this, anyway? Summary Chapter 2—Primitive Data Types Bytes in Memory Variables, Values, and Identifiers Place-Value Number Systems Binary notation Hexadecimal notation Octal notation Integers ints Long, short, and byte Floating-Point Numbers Representing floating-point numbers in binary code Special values Denormalized floating-point numbers CHAR ASCII ISO Latin-1 Unicode UTF8 Boolean Cross-Platform Issues Byte order Unsigned integers Integer widths Conversions and Casting Using a cast The mechanics of conversion Bit-Level Operators Some terminology Bitwise operators Bit shift operators Summary Chapter 2—Primitive Data Types Bytes in Memory Variables, Values, and Identifiers Place-Value Number Systems Binary notation Hexadecimal notation Octal notation Integers ints Long, short, and byte Floating-Point Numbers Representing floating-point numbers in binary code
    [Show full text]
  • Lecture Slides
    Outline Meta-Classes Guy Wiener Introduction AOP Classes Generation 1 Introduction Meta-Classes in Python Logging 2 Meta-Classes in Python Delegation Meta-Classes vs. Traditional OOP 3 Meta-Classes vs. Traditional OOP Outline Meta-Classes Guy Wiener Introduction AOP Classes Generation 1 Introduction Meta-Classes in Python Logging 2 Meta-Classes in Python Delegation Meta-Classes vs. Traditional OOP 3 Meta-Classes vs. Traditional OOP What is Meta-Programming? Meta-Classes Definition Guy Wiener Meta-Program A program that: Introduction AOP Classes One of its inputs is a program Generation (possibly itself) Meta-Classes in Python Its output is a program Logging Delegation Meta-Classes vs. Traditional OOP Meta-Programs Nowadays Meta-Classes Guy Wiener Introduction AOP Classes Generation Compilers Meta-Classes in Python Code Generators Logging Delegation Model-Driven Development Meta-Classes vs. Traditional Templates OOP Syntactic macros (Lisp-like) Meta-Classes The Problem With Static Programming Meta-Classes Guy Wiener Introduction AOP Classes Generation Meta-Classes How to share features between classes and class hierarchies? in Python Logging Share static attributes Delegation Meta-Classes Force classes to adhere to the same protocol vs. Traditional OOP Share code between similar methods Meta-Classes Meta-Classes Guy Wiener Introduction AOP Classes Definition Generation Meta-Classes in Python Meta-Class A class that creates classes Logging Delegation Objects that are instances of the same class Meta-Classes share the same behavior vs. Traditional OOP Classes that are instances of the same meta-class share the same behavior Meta-Classes Meta-Classes Guy Wiener Introduction AOP Classes Definition Generation Meta-Classes in Python Meta-Class A class that creates classes Logging Delegation Objects that are instances of the same class Meta-Classes share the same behavior vs.
    [Show full text]
  • Data Types and Variables
    Color profile: Generic CMYK printer profile Composite Default screen Complete Reference / Visual Basic 2005: The Complete Reference / Petrusha / 226033-5 / Chapter 2 2 Data Types and Variables his chapter will begin by examining the intrinsic data types supported by Visual Basic and relating them to their corresponding types available in the .NET Framework’s Common TType System. It will then examine the ways in which variables are declared in Visual Basic and discuss variable scope, visibility, and lifetime. The chapter will conclude with a discussion of boxing and unboxing (that is, of converting between value types and reference types). Visual Basic Data Types At the center of any development or runtime environment, including Visual Basic and the .NET Common Language Runtime (CLR), is a type system. An individual type consists of the following two items: • A set of values. • A set of rules to convert every value not in the type into a value in the type. (For these rules, see Appendix F.) Of course, every value of another type cannot always be converted to a value of the type; one of the more common rules in this case is to throw an InvalidCastException, indicating that conversion is not possible. Scalar or primitive types are types that contain a single value. Visual Basic 2005 supports two basic kinds of scalar or primitive data types: structured data types and reference data types. All data types are inherited from either of two basic types in the .NET Framework Class Library. Reference types are derived from System.Object. Structured data types are derived from the System.ValueType class, which in turn is derived from the System.Object class.
    [Show full text]
  • Haskell-Style Type Classes with Isabelle/Isar
    Isar ∀ Isabelle= α λ β → Haskell-style type classes with Isabelle/Isar Florian Haftmann 20 February 2021 Abstract This tutorial introduces Isar type classes, which are a convenient mech- anism for organizing specifications. Essentially, they combine an op- erational aspect (in the manner of Haskell) with a logical aspect, both managed uniformly. 1 INTRODUCTION 1 1 Introduction Type classes were introduced by Wadler and Blott [8] into the Haskell lan- guage to allow for a reasonable implementation of overloading1. As a canon- ical example, a polymorphic equality function eq :: α ) α ) bool which is overloaded on different types for α, which is achieved by splitting introduc- tion of the eq function from its overloaded definitions by means of class and instance declarations: 2 class eq where eq :: α ) α ) bool instance nat :: eq where eq 0 0 = True eq 0 - = False eq - 0 = False eq (Suc n)(Suc m) = eq n m instance (α::eq; β::eq) pair :: eq where eq (x1; y1) (x2; y2) = eq x1 x2 ^ eq y1 y2 class ord extends eq where less-eq :: α ) α ) bool less :: α ) α ) bool Type variables are annotated with (finitely many) classes; these annotations are assertions that a particular polymorphic type provides definitions for overloaded functions. Indeed, type classes not only allow for simple overloading but form a generic calculus, an instance of order-sorted algebra [5, 6, 10]. From a software engineering point of view, type classes roughly correspond to interfaces in object-oriented languages like Java; so, it is naturally desirable that type classes do not only provide functions (class parameters) but also state specifications implementations must obey.
    [Show full text]
  • Static Typing Where Possible, Dynamic Typing When Needed: the End of the Cold War Between Programming Languages
    Intended for submission to the Revival of Dynamic Languages Static Typing Where Possible, Dynamic Typing When Needed: The End of the Cold War Between Programming Languages Erik Meijer and Peter Drayton Microsoft Corporation Abstract Advocates of dynamically typed languages argue that static typing is too rigid, and that the softness of dynamically lan- This paper argues that we should seek the golden middle way guages makes them ideally suited for prototyping systems with between dynamically and statically typed languages. changing or unknown requirements, or that interact with other systems that change unpredictably (data and application in- tegration). Of course, dynamically typed languages are indis- 1 Introduction pensable for dealing with truly dynamic program behavior such as method interception, dynamic loading, mobile code, runtime <NOTE to="reader"> Please note that this paper is still very reflection, etc. much work in progress and as such the presentation is unpol- In the mother of all papers on scripting [16], John Ousterhout ished and possibly incoherent. Obviously many citations to argues that statically typed systems programming languages related and relevant work are missing. We did however do our make code less reusable, more verbose, not more safe, and less best to make it provocative. </NOTE> expressive than dynamically typed scripting languages. This Advocates of static typing argue that the advantages of static argument is parroted literally by many proponents of dynami- typing include earlier detection of programming mistakes (e.g. cally typed scripting languages. We argue that this is a fallacy preventing adding an integer to a boolean), better documenta- and falls into the same category as arguing that the essence of tion in the form of type signatures (e.g.
    [Show full text]
  • OMG Meta Object Facility (MOF) Core Specification
    Date : October 2019 OMG Meta Object Facility (MOF) Core Specification Version 2.5.1 OMG Document Number: formal/2019-10-01 Standard document URL: https://www.omg.org/spec/MOF/2.5.1 Normative Machine-Readable Files: https://www.omg.org/spec/MOF/20131001/MOF.xmi Informative Machine-Readable Files: https://www.omg.org/spec/MOF/20131001/CMOFConstraints.ocl https://www.omg.org/spec/MOF/20131001/EMOFConstraints.ocl Copyright © 2003, Adaptive Copyright © 2003, Ceira Technologies, Inc. Copyright © 2003, Compuware Corporation Copyright © 2003, Data Access Technologies, Inc. Copyright © 2003, DSTC Copyright © 2003, Gentleware Copyright © 2003, Hewlett-Packard Copyright © 2003, International Business Machines Copyright © 2003, IONA Copyright © 2003, MetaMatrix Copyright © 2015, Object Management Group Copyright © 2003, Softeam Copyright © 2003, SUN Copyright © 2003, Telelogic AB Copyright © 2003, Unisys USE OF SPECIFICATION - TERMS, CONDITIONS & NOTICES The material in this document details an Object Management Group specification in accordance with the terms, conditions and notices set forth below. This document does not represent a commitment to implement any portion of this specification in any company's products. The information contained in this document is subject to change without notice. LICENSES The companies listed above have granted to the Object Management Group, Inc. (OMG) a nonexclusive, royalty-free, paid up, worldwide license to copy and distribute this document and to modify this document and distribute copies of the modified version. Each of the copyright holders listed above has agreed that no person shall be deemed to have infringed the copyright in the included material of any such copyright holder by reason of having used the specification set forth herein or having conformed any computer software to the specification.
    [Show full text]
  • Software II: Principles of Programming Languages
    Software II: Principles of Programming Languages Lecture 6 – Data Types Some Basic Definitions • A data type defines a collection of data objects and a set of predefined operations on those objects • A descriptor is the collection of the attributes of a variable • An object represents an instance of a user- defined (abstract data) type • One design issue for all data types: What operations are defined and how are they specified? Primitive Data Types • Almost all programming languages provide a set of primitive data types • Primitive data types: Those not defined in terms of other data types • Some primitive data types are merely reflections of the hardware • Others require only a little non-hardware support for their implementation The Integer Data Type • Almost always an exact reflection of the hardware so the mapping is trivial • There may be as many as eight different integer types in a language • Java’s signed integer sizes: byte , short , int , long The Floating Point Data Type • Model real numbers, but only as approximations • Languages for scientific use support at least two floating-point types (e.g., float and double ; sometimes more • Usually exactly like the hardware, but not always • IEEE Floating-Point Standard 754 Complex Data Type • Some languages support a complex type, e.g., C99, Fortran, and Python • Each value consists of two floats, the real part and the imaginary part • Literal form real component – (in Fortran: (7, 3) imaginary – (in Python): (7 + 3j) component The Decimal Data Type • For business applications (money)
    [Show full text]
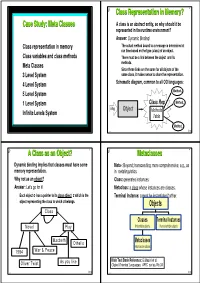
  • Metaclasses 4 ◆ Dynamic Binding Implies That Classes Must Have Some ◆ Meta-: Beyond; Transcending; More Comprehensive; E.G., As Memory Representation
    ® 1 ® Class Representation in Memory? 2 Case Study: Meta Classes ◆ A class is an abstract entity, so why should it be represented in the runtime environment? ◆ Answer: Dynamic Binding! ◆ Class representation in memory ● The actual method bound to a message is determined at run time based on the type (class) of an object. ◆ Class variables and class methods ● There must be a link between the object and its ◆ Meta Classes methods. ● Since these links are the same for all objects of the ◆ 3 Level System same class, it makes sense to share the representation. ◆ ◆ 4 Level System Schematic diagram, common to all OO languages: Method ◆ 5 Level System 1 Method ◆ 1 Level System Class Rep 2 ◆ Msg Object Methods Infinite Levels System Table Methodn oop Õ Ö oop Õ Ö ® A Class as an Object? 3 ® Metaclasses 4 ◆ Dynamic binding implies that classes must have some ◆ Meta-: Beyond; transcending; more comprehensive; e.g., as memory representation. in metalinguistics. ◆ Why not as an object? ◆ Class: generates instances. ◆ Answer: Let's go for it! ◆ Metaclass: a class whose instances are classes. ● Each object o has a pointer to its class object c which is the ◆ Terminal Instance: cannot be instantiated further. object representing the class to which o belongs. Objects Class Classes Terminal Instances Novel Play Instantiable objects Non instantiable objects Macbeth Othello Metaclasses Instances are classes 1984 War & Peace As you like Main Text Book Reference: G.Masini et al. Oliver Twist Object-Oriented Languages, APIC series, No.34 oop Õ Ö oop Õ Ö ® 5 ® 6 Taxonomy of Metaclass Systems The 3 Level System ◆ 1-Level System: Objects only Object ● Each object describes itself INSTANCE _OF ● No need for classes: objects are ìinstantiatedî or ìinheritedî from SUBCLASS _OF other objects Class Example: Self VARIABLES instance_of ,167$1&(B2) ◆ 2-Level System: Objects, Classes METHODS ..
    [Show full text]
  • Should Your Specification Language Be Typed?
    Should Your Specification Language Be Typed? LESLIE LAMPORT Compaq and LAWRENCE C. PAULSON University of Cambridge Most specification languages have a type system. Type systems are hard to get right, and getting them wrong can lead to inconsistencies. Set theory can serve as the basis for a specification lan- guage without types. This possibility, which has been widely overlooked, offers many advantages. Untyped set theory is simple and is more flexible than any simple typed formalism. Polymorphism, overloading, and subtyping can make a type system more powerful, but at the cost of increased complexity, and such refinements can never attain the flexibility of having no types at all. Typed formalisms have advantages too, stemming from the power of mechanical type checking. While types serve little purpose in hand proofs, they do help with mechanized proofs. In the absence of verification, type checking can catch errors in specifications. It may be possible to have the best of both worlds by adding typing annotations to an untyped specification language. We consider only specification languages, not programming languages. Categories and Subject Descriptors: D.2.1 [Software Engineering]: Requirements/Specifica- tions; D.2.4 [Software Engineering]: Software/Program Verification—formal methods; F.3.1 [Logics and Meanings of Programs]: Specifying and Verifying and Reasoning about Pro- grams—specification techniques General Terms: Verification Additional Key Words and Phrases: Set theory, specification, types Editors’ introduction. We have invited the following
    [Show full text]
  • A Core Calculus of Metaclasses
    A Core Calculus of Metaclasses Sam Tobin-Hochstadt Eric Allen Northeastern University Sun Microsystems Laboratories [email protected] [email protected] Abstract see the problem, consider a system with a class Eagle and Metaclasses provide a useful mechanism for abstraction in an instance Harry. The static type system can ensure that object-oriented languages. But most languages that support any messages that Harry responds to are also understood by metaclasses impose severe restrictions on their use. Typi- any other instance of Eagle. cally, a metaclass is allowed to have only a single instance However, even in a language where classes can have static and all metaclasses are required to share a common super- methods, the desired relationships cannot be expressed. For class [6]. In addition, few languages that support metaclasses example, in such a language, we can write the expression include a static type system, and none include a type system Eagle.isEndangered() provided that Eagle has the ap- with nominal subtyping (i.e., subtyping as defined in lan- propriate static method. Such a method is appropriate for guages such as the JavaTM Programming Language or C#). any class that is a species. However, if Salmon is another To elucidate the structure of metaclasses and their rela- class in our system, our type system provides us no way of tionship with static types, we present a core calculus for a requiring that it also have an isEndangered method. This nominally typed object-oriented language with metaclasses is because we cannot classify both Salmon and Eagle, when and prove type soundness over this core.
    [Show full text]