Modelling the Response of Placentia Bay to Hurricanes Igor and Leslie
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
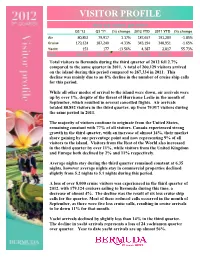
Visitor Profile
` VISITOR PROFILE How did visitors get here? Q3 '12 Q3 '11 (%) change 2012 YTD 2011 YTD (%) change Air 80,852 79,917 1.17% 187,657 191,203 -1.85% Cruise 179,124 187,240 -4.33% 343,194 348,951 -1.65% Yacht 153 177 -13.56% 4,387 2,817 55.73% Total 260,129 267,334 -2.70% 535,238 542,971 -1.42% Total visitors to Bermuda during the third quarter of 2012 fell 2.7% compared to the same quarter in 2011. A total of 260,129 visitors arrived on the island during this period compared to 267,334 in 2011. This decline was mainly due to an 8% decline in the number of cruise ship calls for this period. While all other modes of arrival to the island were down, air arrivals were up by over 1%, despite of the threat of Hurricane Leslie in the month of September, which resulted in several cancelled flights. Air arrivals totaled 80,852 visitors in the third quarter, up from 79,917 visitors during the same period in 2011. The majority of visitors continue to originate from the United States, remaining constant with 77% of all visitors. Canada experienced strong growth in the third quarter, with an increase of almost 14%, their market share gaining by one percentage point and now representing 9% of all visitors to the island. Visitors from the Rest of the World also increased in the third quarter by over 11%, while visitors from the United Kingdom and Europe both declined by 2% and 11% respectively. -

Capital Adequacy (E) Task Force RBC Proposal Form
Capital Adequacy (E) Task Force RBC Proposal Form [ ] Capital Adequacy (E) Task Force [ x ] Health RBC (E) Working Group [ ] Life RBC (E) Working Group [ ] Catastrophe Risk (E) Subgroup [ ] Investment RBC (E) Working Group [ ] SMI RBC (E) Subgroup [ ] C3 Phase II/ AG43 (E/A) Subgroup [ ] P/C RBC (E) Working Group [ ] Stress Testing (E) Subgroup DATE: 08/31/2020 FOR NAIC USE ONLY CONTACT PERSON: Crystal Brown Agenda Item # 2020-07-H TELEPHONE: 816-783-8146 Year 2021 EMAIL ADDRESS: [email protected] DISPOSITION [ x ] ADOPTED WG 10/29/20 & TF 11/19/20 ON BEHALF OF: Health RBC (E) Working Group [ ] REJECTED NAME: Steve Drutz [ ] DEFERRED TO TITLE: Chief Financial Analyst/Chair [ ] REFERRED TO OTHER NAIC GROUP AFFILIATION: WA Office of Insurance Commissioner [ ] EXPOSED ________________ ADDRESS: 5000 Capitol Blvd SE [ ] OTHER (SPECIFY) Tumwater, WA 98501 IDENTIFICATION OF SOURCE AND FORM(S)/INSTRUCTIONS TO BE CHANGED [ x ] Health RBC Blanks [ x ] Health RBC Instructions [ ] Other ___________________ [ ] Life and Fraternal RBC Blanks [ ] Life and Fraternal RBC Instructions [ ] Property/Casualty RBC Blanks [ ] Property/Casualty RBC Instructions DESCRIPTION OF CHANGE(S) Split the Bonds and Misc. Fixed Income Assets into separate pages (Page XR007 and XR008). REASON OR JUSTIFICATION FOR CHANGE ** Currently the Bonds and Misc. Fixed Income Assets are included on page XR007 of the Health RBC formula. With the implementation of the 20 bond designations and the electronic only tables, the Bonds and Misc. Fixed Income Assets were split between two tabs in the excel file for use of the electronic only tables and ease of printing. However, for increased transparency and system requirements, it is suggested that these pages be split into separate page numbers beginning with year-2021. -

2018 Climate Summary
& ~ Hurricane Season Review ~ Meteorological Department St. Maarten Modesta Drive # 12, Simpson Bay (721) 545-4226 www.meteosxm.com MDS Climatological Summary 2018 The information contained in this Climatological Summary must not be copied in part or any form, or communicated for the use of any other party without the expressed written permission of the Meteorological Department St. Maarten. All data and observations were recorded at the Princess Juliana International Airport. This document is published by the Meteorological Department St. Maarten, and a digital copy is available on our website. Prepared by: Sheryl Etienne-Leblanc Published by: Meteorological Department St. Maarten Modesta Drive # 12, Simpson Bay St. Maarten, Dutch Caribbean Telephone: (721) 545-4226 Website: www.meteosxm.com E-mail: [email protected] www.facebook.com/sxmweather www.twitter.com/@sxmweather MDS © May 2019 Page 2 of 29 MDS Climatological Summary 2018 Table of Contents Introduction.............................................................................................................. 4 Island Climatology……............................................................................................. 5 About Us……………………………………………………………………………..……….……………… 6 2018 Hurricane Season Summary…………………………………………………………………………………………….. 8 Local Effects...................................................................................................... 9 Summary Table ............................................................................................... -

CMOS Bulletin SCMO Volume 41 No. 1 February 2013
ISSN 1929-7726 (Online / En ligne) ISSN 1195-8898 (Print / Imprimé) . CMOS Canadian Meteorological BULLETIN and Oceanographic Society SCMO La Société canadienne de météorologie et February / février 2013 Vol.41 No.1 d'océanographie NOAA satellite image of Hurricane Sandy Image satellitaire de l’ouragan Sandy pris par NOAA Canadian Meteorological and Oceanographic Society Société canadienne de météorologie et d’océanographie ....from the President’s Desk / Allocution du président CMOS Bulletin SCMO Volume 41 No.1 Friends and colleagues: February 2013 — février 2013 This is the issue of the Inside / En Bref Bulletin where I should urge all you from the President’s desk procrastinators to renew Allocution du président your membership! In by/par Perter Bartello page 001 addition, it is time for us all to start making Cover page description arrangements to attend Description de la page couverture page 002 the upcoming Saskatoon congress. It will be a Articles joint meeting with the 2012: Record Arctic Sea Ice Melt, Multiple Canadian Geophysical Extremes and High Temperatures page 005 Union and the Canadian Water Resources Determining Cloud Base using an IR Association and will host Thermometer page 007 special sessions dedicated to 2013s WMO highlights pivotal role of carbon sinks page 008 Peter Bartello identification as the year CMOS President Rôle crucial joué par les puits de carbone Président de la SCMO of Mathematics of Planet Earth. It therefore seems selon l’OMM page 009 clear it will be another in a recent string of excellent CMOS Canada’s Top Ten Weather Stories for 2012 congresses and I look forward to the stimulating discussion. -

Forecast of Atlantic Hurricane Activity For
SUMMARY OF 2012 ATLANTIC TROPICAL CYCLONE ACTIVITY AND VERIFICATION OF AUTHORS' SEASONAL AND TWO-WEEK FORECASTS The 2012 hurricane season had more activity than predicted in our seasonal forecasts. It was notable for having a very large number of weak, high latitude tropical cyclones but only one major hurricane. The activity that occurred in 2012 was anomalously concentrated in the northeast subtropical Atlantic. While Superstorm Sandy caused massive devastation along parts of the mid-Atlantic and Northeast coast, its destruction was viewed to be within the realm of natural variability. By Philip J. Klotzbach1 and William M. Gray2 This forecast as well as past forecasts and verifications are available via the World Wide Web at http://hurricane.atmos.colostate.edu Emily Wilmsen, Colorado State University Media Representative, (970-491-6432) is available to answer various questions about this verification. Department of Atmospheric Science Colorado State University Fort Collins, CO 80523 Email: [email protected] As of 29 November 2012 1 Research Scientist 2 Professor Emeritus of Atmospheric Science 1 ATLANTIC BASIN SEASONAL HURRICANE FORECASTS FOR 2012 Forecast Parameter and 1981-2010 Median 4 April 2012 Update Update Observed % of 1981- (in parentheses) 1 June 2012 3 Aug 2012 2012 Total 2010 Median Named Storms (NS) (12.0) 10 13 14 19 158% Named Storm Days (NSD) (60.1) 40 50 52 99.50 166% Hurricanes (H) (6.5) 4 5 6 10 154% Hurricane Days (HD) (21.3) 16 18 20 26.00 122% Major Hurricanes (MH) (2.0) 2 2 2 1 50% Major Hurricane Days -

Title Goes Here
DANIEL HERNANDEZ PARTNER Shutts & Bowen LLP 4301 W. Boy Scout Boulevard Suite 300 Tampa, Florida 33607 DIRECT (813) 227-8114 FAX (813) 227-8214 EMAIL [email protected] FILED 11/22/2019 November 22, 2019 DOCUMENT NO. 11075-2019 FPSC - COMMISSION CLERK VIA ELECTRONIC FILING Mr. Adam Teitzman, Commission Clerk Florida Public Service Commission 2540 Shumard Oak Boulevard Tallahassee, FL 32399-0850 In re: Petition by Duke Energy Florida, LLC for Approval of Actual Storm Restoration Costs and Associated Recovery Process Related to Hurricane Michael and Tropical Storm Alberto (th e "Petition"); Docket No. 20190110-EI. Dear Mr. Teitzman: On behalf of Duke Energy Florida, LLC ("DEF"), please find the enclosed for electronic filing in the above-referenced proceeding: • DEF's Petition for approval of actual storm restoration costs and associated recovery process related to Hurricane Michael and Tropical Storm Alberto; • Direct Testimony of Tom Morris with Exhibit No._ (TM-1), Exhibit No._ (TM-2), and Exhibit No._· (TM-3); • Direct Testimony of Jason Cutliffe with Exhibit No._ (JC-1), Exhibit No._ (JC-2), and Exhibit No._ (JC-3); and • Direct Testimony of Jason S. Williams. Thank you for your assistance in this matter. Please feel free to call me at (81 3) 227- 8114 should you have any questions concerning this filing. Respectfully, Shutts & Bowen LLP Daniel Hernandez Enclosures (as noted) cc : All counsel for DEF shutts.com I FO RT LAUD ER DALE I JACKSONVILLE I MIAMI I ORLANDO I SARA SOTA I TALLAHA SSEE I TAM PA I WEST PA LM BEACH BEFORE THE FLORIDA PUBLIC SERVICE COMMISSION Docket No. -

Hurricane Leslie
HURRICANE TRACKING ADVISORY eVENT™ Hurricane Leslie Information from NHC Advisory 28, 5:00 AM EDT Thursday September 6, 2012 Hurricane Leslie is a moving slowly north-northwestward with a gradual strengthening forecast over the next 48 hours. Intensity Measures Position & Heading Landfall Forecast (NHC) Max Sustained Wind 75 mph Position Relative to 440 miles SSE of Bermuda Speed: (cat 1) Land: Est. Time & Region: n/a Min Central Pressure: 985 mb Coordinates: 26.3 N, 62.4 W Hurricane Force Est. Max Sustained Wind 25 miles Bearing/Speed: N or 360 degrees at 1 mph n/a Winds (74+ mph): Speed: Forecast Summary Within 48 hours, there is a 80% chance Leslie will remain at hurricane strength (74+ mph winds), a 20% chance Leslie will weaken to a tropical storm (39-73 mph winds) and a less than 1% chance Leslie will weaken to tropical depression strength or dissipate (winds below 39 mph). The windfield map – based on the AVNO forecast (below right) – shows that this model has forecast the storm’s peak winds at category 3 hurricane strength (111-129 mph winds). The AVNO – one of many models used by NOAA – has been statistically identified as the current “best performing” model for Hurricane Leslie by Kinetic Analysis Corp. Forecast tracks for all current models (All Fcst Tracks) are shown on the map (in pale gray) to illustrate the uncertainty in Leslie’s forecast track. Swells generated by Leslie are continuing to affect Bermuda, the US East coast from Central Florida northward, the northern Leeward Islands, Puerto Rico, and the Virgin Islands. -

The University of Rhode Island Award Period: 08/01/2011
NOAA Award Number: NA11OAR4310196 Recipient Name: The University of Rhode Island Award Period: 08/01/2011 - 07/31/2013 Program Office: OAR Office of Weather and Air Quality (OWAQ) Project Title: Improving the Operational Tropical Cyclone Models at NOAA/NCEP and Navy/FNMOC PIs/PDs: Isaac Ginis and Morris Bender Report Type: Final Report Reporting Period: 08/01/2011 - 07/31/2013 In this final report, we summarize the main results accomplished during this two-year project and the upgrades implemented into the operational GFDL and GFDN models for the 2012 and 2013 seasons. We also describe the upgrades prepared for the operational implementations at NCEP and FNMOC for the upcoming 2014 hurricane/typhoon/tropical cyclone seasons. a) Implemented a unified GFDL/GFDN version control framework. It has been recognized that a unified GFDL/GFDN code system with version control will result in a more efficient transition to operations when improvements are made to one of the versions of the model. To accomplish this unification, we have incorporated the Subversion (svn) software system into GFDL/GFDN on the URI computing cluster, and we are helping to setup the GFDL and GFDN systems under Subversion control at NCEP and FNMOC to track future changes to all of the various components of the forecast systems. It is anticipated that this work will reduce the possibility of coding errors introduced during future implementations. b) Absolved the need for NHC’s active participation in the ocean model initialization. During the 2012 Atlantic hurricane season, it became clear that NHC did not always have the time or resources to regularly update the Loop Current and Loop Current eddy files associated with the feature-based ocean model initialization procedure, especially during potentially high-impact events when up-to-date versions of these files are most needed. -

Climatological Summary 2012
Climatological Summary 2012 ~ Including Hurricane Season Review ~ Meteorological Department St. Maarten Airport Rd. # 69, Simpson Bay (721) 545-2024 or (721) 545-4226 www.meteosxm.com The information contained in this Climatological Summary must not be copied in part or any form, or communicated for the use of any other party without the expressed written permission of the Meteorological Department St. Maarten. All data and observations were recorded at the Princess Juliana International Airport. This document is published by the Meteorological Department St. Maarten, and a digital copy is available on our website. All rights of the enclosed information remain the property of: Meteorological Department St. Maarten Airport Road #69, Simpson Bay St. Maarten, Dutch Caribbean Prepared by: Desiree Connor, MDS Climatology Section Sheryl Etienne-LeBlanc, MDS Forecast Section Telephone: (721) 545-2024 or (721) 545-4226 Fax: (721) 545-2998 Website: www.meteosxm.com E-mail: [email protected] Property of Meteorological Department St. Maarten, © January 2013 Page 2 of 22 Table of Contents Introduction.....................................................................................................................................4 About Us...........................................................................................................................................5 Hurricane Season.............................................................................................................................7 Oddities.................................................................................................................................7 -

PCI 2012 Atlantic Hurrican Season Overview
2012 Atlantic Hurricane Season Overview Superstorm Sandy Slammed the East Coast Resulting in Record-Setting Damage Hurricane season 2012 will go into the history books as another active year for tropical storms. With 19 named storms and 10 hurricanes, forecasters were very accurate predicting 12-17 named storms including 5-8 hurricanes. The United States was fortunate that only three tropical storms and one hurricane made landfall in 2012. 2012 Atlantic Hurricane Season Storms Top 10 Hurricanes 1. Tropical Storm Alberto This background information provides you with 2. Tropical Storm Beryl some historical data regarding catastrophic events 3. Hurricane Chris in the United States. 4. Tropical Storm Debby 5. Hurricane Ernesto Top 10 Hurricanes and Estimated Insured Loss 6. Tropical Storm Florence (adjusted to 2011 dollars): 7. Tropical Storm Helene Year Event Insured Loss 8. Hurricane Gordon 2005 Katrina $46.6 billion 9. Hurricane Isaac 1992 Andrew $22.9 billion 10. Tropical Storm Joyce 2008 Ike $13.1 billion 11. Hurricane Kirk 2005 Wilma $11.7 billion 12. Hurricane Leslie 2004 Charley $ 8.8 billion 13. Hurricane Michael 2004 Ivan $ 8.3 billion 14. Hurricane Nadine 1989 Hugo $ 6.8 billion 15. Tropical Storm Oscar 2005 Rita $ 6.4 billion 16. Tropical Storm Patty 2004 Frances $ 5.4 billion 17. Hurricane Rafael 2011 Irene $ 4.3 billion 18. Hurricane Sandy (Source: Insurance Information Institute and Property 19. Tropical Storm Tony Claim Services) This year’s Storm Activity Actions for Homeowners Tropical Storm Beryl made US landfall May 29, in To prevent the loss of life and minimize property Jacksonville Beach, Florida, as the strongest pre- damage it is vital that coastal residents create a season Atlantic tropical cyclone on record. -

Downloaded 10/06/21 09:29 AM UTC OCTOBER 2015 Z a R Z Y C K I a N D J a B L O N O W S K I 4013 of Physical Parameterizations, Potentially Introducing 2
4012 MONTHLY WEATHER REVIEW VOLUME 143 Experimental Tropical Cyclone Forecasts Using a Variable-Resolution Global Model COLIN M. ZARZYCKI National Center for Atmospheric Research,* Boulder, Colorado CHRISTIANE JABLONOWSKI Department of Atmospheric, Oceanic, and Space Sciences, University of Michigan, Ann Arbor, Michigan (Manuscript received 20 April 2015, in final form 5 July 2015) ABSTRACT Tropical cyclone (TC) forecasts at Dx ; 14-km horizontal resolution (0.1258) are completed using variable- resolution (V-R) grids within the Community Atmosphere Model (CAM). Forecasts are integrated twice daily from 1 August to 31 October for both 2012 and 2013, with a high-resolution nest centered over the North Atlantic and eastern Pacific Ocean basins. Using the CAM version 5 (CAM5) physical parameterization package, regional refinement is shown to significantly increase TC track forecast skill relative to unrefined grids (Dx ; 55 km, 0.58). For typical TC forecast integration periods (approximately 1 week), V-R forecasts are able to nearly identically reproduce the flow field of a globally uniform high-resolution forecast. Simulated intensity is generally too strong for forecasts beyond 72 h. This intensity bias is robust regardless of whether the forecast is forced with observed or climatological sea surface temperatures and is not significantly miti- gated in a suite of sensitivity simulations aimed at investigating the impact of model time step and CAM’s deep convection parameterization. Replacing components of the default physics with Cloud Layers Unified by Binormals (CLUBB) produces a statistically significant improvement in forecast intensity at longer lead times, although significant structural differences in forecasted TCs exist. CAM forecasts the recurvature of Hurricane Sandy into the northeastern United States 60 h earlier than the Global Forecast System (GFS) model using identical initial conditions, demonstrating the sensitivity of TC forecasts to model configuration. -

National Situation Report As of 5:30 A.M
National Situation Report As of 5:30 a.m. (EDT) Thursday, September 6, 2012 This information is published as a public service by the FEMA National Watch Center (NWC). Information presented is considered public information and may be distributed or copied. For questions or comments, contact the NWC at fema-nwc- [email protected]. Media inquiries should be directed to FEMA News Desk (available 24/7): [email protected]. Significant National Weather: See http://weather.gov/ for the latest information. Northeast A cold front extending from the Great Lakes southwestward to the Southern Plains will move slowly eastward to the Northeast Coast, producing showers and thunderstorms from the Great Lakes to western Pennsylvania and much of western and northern New York State today and moving into the Eastern Seaboard by Friday. Along the coast, increasing swells from distant Hurricane Leslie will result in higher surf on the beaches through the end of the week and into the weekend. South Over Texas, Oklahoma, and into the Lower Mississippi River Valley, very hot weather is expected to continue for a few more days before a cold front brings badly needed relief this weekend. Daytime highs of 100-105 degrees are expected for Oklahoma and much of central and northern Texas. Highs in the mid to upper 90s, along with oppressive levels of humidity, are likely for Arkansas, Louisiana, and Mississippi, resulting in heat advisories for portions of these states. Isolated afternoon and evening thunderstorms are possible across the Southern Plains; a few storms could be severe from the Texas and Oklahoma Panhandles into Kansas.