DOCSLIB.ORG

Energy Surfaces and Kinetic Analyses

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Energy Surfaces and Kinetic Analyses Chapter 7 Energy Surfaces and Kinetic Analyses Chapters 7 and 8: learning tools to use deciphering reaction mechanisms -> a mechanism can never really be proven. 7.1 Energy surfaces and related concepts Kinetics of a reaction: determine how quickly product forms as a function of concentrations, temperature, and other variables. -> goal is to relate experimental observations to molecular scale concepts, such as molecular motions, molecular collisions, and molecular vibrations, as well as energy concepts such as free energy, enthalpy, and entropy. Reaction dynamics: the molecular scale analysis of reaction rates. When we are talking about individual (or small groups of) molecules traversing a well-defined surface, we will tend to call such analyses “dynamics studies”. Discussion of macroscopic measurements of real reacting systems will be termed “kinetics”. 7.1.1 Energy surface 7.1.2 Reaction coordinate diagrams Reaction coordinate: the minimum energy pathways, or the pathway we depict as the weighted average of all the pathways Reaction coordinate diagram Intermediates: any chemical structures that last longer than the time for a typical bond vibration (10-13 to 10-14 s) Rate-determining step: the step with the highest barrier. Activation energy 7.1.4 Rates and rate constants Rate constant (k): a proportionality constant between concentration of reactants and reaction rate 7.1.5 Reaction order and rate laws Rate constant (k): a proportionality constant between concentration of reactants and reaction rate a + b + c = reaction order Rate law -> determined by experimental measurements of the rates of reaction: does not give any information about mechanism Molecularity: the number of molecules involved in the transition state of the reaction Elementary reaction: single-step reaction (단일반응) Unimolecular: only single molecule is involved in the transition state, eg) Cope rearrangement Bimolecular: two molecules are involved in the transition state, eg) SN2 Termolecular: three molecules are involved in the transition state Molecularity applies only to elementary reactions and is basically a statement about the mechanism of the reaction. 7.2 Transition state theory and related topics 7.2.1 The mathematics of transition state theory: pre-equilibrium between the reactants and activated complex To understand the nature of the rate constant k -> analyze the energetic and entropic components of reaction process + k+ + A + B ←→ [AB ] → C + AB+ rate = + + [AB + ] Equilibrium constant of the K+ = [A][B] formation of activated complex A + B C + + = kK+ +[A][B] + + + + + + ΔG += ΔH + - TΔS + = -RTnK + K + = e -ΔG /RT κk T + rate = B e -ΔG /RT [A][B] h κ: transmission coefficient ~ 1 = k [A][B] kB: Boltzmann constant h: Planck’s constant κk T + k = B e -ΔG /RT T: absolute temperature h κk T + k = B e -ΔG /RT h + κk T + + = B e -ΔH /RT eΔS/R h + κk + + = B eΔS/R e -ΔH /RT Eyring equation h T + + κk + e -ΔH /RT C = B eΔS/R = C T h 7.2.2 Relationship to the Arrhenius rate law Arrhenius rate law A: frequency factor (pre-exponential factor) Ea: activation energy T: absolute temperature Eyring equation: analyzes a microscopic rate constant for a single-step conversion of a reactant to a product. In a multistep process involving reactive intermediates, there is an Eyring equation and thus a ΔG‡ for each and every step. Arrhenius rate law: arises from empirical observations of the macroscopic rate constants for a particular conversion, such as A going to B by various paths. It is ignorant of any mechanistic considerations, such as whether one or more reactive intermediates are involved in the overall conversion of A to B. Ea describes the overall transformation. 7.2.3 Boltzmann distributions and temperature dependence The higher temperature reaction proceeds faster due to the larger area under the curve past the activation energy Boltzmann distribution 7.2.5 Experimental determinations of activation parameters and Arrhenius parameters Eyring equation Arrhenius equation T -> k ---Æ ΔH‡, ΔS‡, ΔG‡ 7.2.6 Examples of activation parameters and their interpretations + Diels-Alder reaction Gas phase ΔH‡ = 15.5 kcal/mol ΔS‡ = -34 eu Bu NNBu 2 Bu + N2 Gas phase ΔH‡ = 52 kcal/mol ΔS‡ = 19 eu ΔH‡ : the latter > the former why? the former; concerted reaction -> bond making accompanies bond breaking ΔS‡ : the latter > the former why? The former -> two molecules become one molecule -> the loss of translational and rotational degrees of freedom the latter -> one molecule becomes three molecules Claisen rearrangement O O O ΔS‡ = -8 eu 1, 2, 4, 6 -> molecules combine 3,5,7 -> bond breaking 1; -26 eu -> 26 cal/mol K x 298 K = 7.75 kcal/mol in ΔG‡ -> decrease in the rate constant by a factor of 500,000, relative to a reaction with a ΔS‡ = 0 7.3 Postulates and principles related to kinetic analysis 7.3.1 Hammond postulate Transition states are transient in nature and generally cannot be directly characterized by experimental means. This postulate is likely the most widely used principle for estimating the structures of activated complexes that give us insights into chemical reactivity. ; the activated complex most resembles the adjacent reactant, intermediate, or product that it is closest in energy to. exothermic endothermic The Hammond postulate does not predict the height of the barrier compared to the reactant and product. 이런 경우도 있다. 그러나 대부분의 경우 To obey the Hammond postulate 7.9와같은reaction coordinates를 갖는다.
Load more

Recommended publications
  • Eyring Equation
    Search Buy/Sell Used Reactors Glass microreactors Hydrogenation Reactor Buy Or Sell Used Reactors Here. Save Time Microreactors made of glass and lab High performance reactor technology Safe And Money Through IPPE! systems for chemical synthesis scale-up. Worldwide supply www.IPPE.com www.mikroglas.com www.biazzi.com Reactors & Calorimeters Induction Heating Reacting Flow Simulation Steam Calculator For Process R&D Laboratories Check Out Induction Heating Software & Mechanisms for Excel steam table add-in for water Automated & Manual Solutions From A Trusted Source. Chemical, Combustion & Materials and steam properties www.helgroup.com myewoss.biz Processes www.chemgoodies.com www.reactiondesign.com Eyring Equation Peter Keusch, University of Regensburg German version "If the Lord Almighty had consulted me before embarking upon the Creation, I should have recommended something simpler." Alphonso X, the Wise of Spain (1223-1284) "Everything should be made as simple as possible, but not simpler." Albert Einstein Both the Arrhenius and the Eyring equation describe the temperature dependence of reaction rate. Strictly speaking, the Arrhenius equation can be applied only to the kinetics of gas reactions. The Eyring equation is also used in the study of solution reactions and mixed phase reactions - all places where the simple collision model is not very helpful. The Arrhenius equation is founded on the empirical observation that rates of reactions increase with temperature. The Eyring equation is a theoretical construct, based on transition state model. The bimolecular reaction is considered by 'transition state theory'. According to the transition state model, the reactants are getting over into an unsteady intermediate state on the reaction pathway.
    [Show full text]
  • The 'Yard Stick' to Interpret the Entropy of Activation in Chemical Kinetics
    World Journal of Chemical Education, 2018, Vol. 6, No. 1, 78-81 Available online at http://pubs.sciepub.com/wjce/6/1/12 ©Science and Education Publishing DOI:10.12691/wjce-6-1-12 The ‘Yard Stick’ to Interpret the Entropy of Activation in Chemical Kinetics: A Physical-Organic Chemistry Exercise R. Sanjeev1, D. A. Padmavathi2, V. Jagannadham2,* 1Department of Chemistry, Geethanjali College of Engineering and Technology, Cheeryal-501301, Telangana, India 2Department of Chemistry, Osmania University, Hyderabad-500007, India *Corresponding author: [email protected] Abstract No physical or physical-organic chemistry laboratory goes without a single instrument. To measure conductance we use conductometer, pH meter for measuring pH, colorimeter for absorbance, viscometer for viscosity, potentiometer for emf, polarimeter for angle of rotation, and several other instruments for different physical properties. But when it comes to the turn of thermodynamic or activation parameters, we don’t have any meters. The only way to evaluate all the thermodynamic or activation parameters is the use of some empirical equations available in many physical chemistry text books. Most often it is very easy to interpret the enthalpy change and free energy change in thermodynamics and the corresponding activation parameters in chemical kinetics. When it comes to interpretation of change of entropy or change of entropy of activation, more often it frightens than enlightens a new teacher while teaching and the students while learning. The classical thermodynamic entropy change is well explained by Atkins [1] in terms of a sneeze in a busy street generates less additional disorder than the same sneeze in a quiet library (Figure 1) [2].
    [Show full text]
  • Estimation of Viscosity Arrhenius Pre-Exponential Factor and Activation Energy of Some Organic Liquids E
    ISSN 2350-1030 International Journal of Recent Research in Physics and Chemical Sciences (IJRRPCS) Vol. 5, Issue 1, pp: (18-26), Month: April 2018 – September 2018, Available at: www.paperpublications.org ESTIMATION OF VISCOSITY ARRHENIUS PRE-EXPONENTIAL FACTOR AND ACTIVATION ENERGY OF SOME ORGANIC LIQUIDS E. IKE1 and S. C. EZIKE2 1,2Department of Physics, Modibbo Adama University of Technology, P. M. B. 2076, Yola, Adamawa State, Nigeria. Corresponding Author‟s E-mail: [email protected] Abstract: Information concerning fluid’s physico-chemical behaviors is of utmost importance in the design, running and optimization of industrial processes, in this regard, the idea of fluid viscosity quickly comes to mind. Models have been proposed in literatures to describe the viscosity of liquids and fluids in general. The Arrhenius type equations have been proposed for pure solvents; correlating the pre-exponential factor A and activation energy Ea. In this paper, we aim at extending these Arrhenius parameters to simple organic liquids such as water, ethanol and Diethyl ether. Hence, statistical method and analysis are applied using viscosity data set from the literature of some organic liquids. The Arrhenius type equation simplifies the estimation of viscous properties and the calculations thereafter. Keywords: Viscosity, organic liquids, Arrhenius parameters, correlation, statistics. 1. INTRODUCTION All fluids are compressible and when flowing are capable of sustaining shearing stress on account of friction between the adjacent layers. Viscosity (η) is the inherent property of all fluids and may be referred to as the internal friction offered by a fluid to the flow. For water in a beaker, when stirred and left to itself, the motion subsides after sometime, which can happen only in the presence of resisting force acting on the fluid.
    [Show full text]
  • Glossary of Terms Used in Photochemistry, 3Rd Edition (IUPAC
    Pure Appl. Chem., Vol. 79, No. 3, pp. 293–465, 2007. doi:10.1351/pac200779030293 © 2007 IUPAC INTERNATIONAL UNION OF PURE AND APPLIED CHEMISTRY ORGANIC AND BIOMOLECULAR CHEMISTRY DIVISION* SUBCOMMITTEE ON PHOTOCHEMISTRY GLOSSARY OF TERMS USED IN PHOTOCHEMISTRY 3rd EDITION (IUPAC Recommendations 2006) Prepared for publication by S. E. BRASLAVSKY‡ Max-Planck-Institut für Bioanorganische Chemie, Postfach 10 13 65, 45413 Mülheim an der Ruhr, Germany *Membership of the Organic and Biomolecular Chemistry Division Committee during the preparation of this re- port (2003–2006) was as follows: President: T. T. Tidwell (1998–2003), M. Isobe (2002–2005); Vice President: D. StC. Black (1996–2003), V. T. Ivanov (1996–2005); Secretary: G. M. Blackburn (2002–2005); Past President: T. Norin (1996–2003), T. T. Tidwell (1998–2005) (initial date indicates first time elected as Division member). The list of the other Division members can be found in <http://www.iupac.org/divisions/III/members.html>. Membership of the Subcommittee on Photochemistry (2003–2005) was as follows: S. E. Braslavsky (Germany, Chairperson), A. U. Acuña (Spain), T. D. Z. Atvars (Brazil), C. Bohne (Canada), R. Bonneau (France), A. M. Braun (Germany), A. Chibisov (Russia), K. Ghiggino (Australia), A. Kutateladze (USA), H. Lemmetyinen (Finland), M. Litter (Argentina), H. Miyasaka (Japan), M. Olivucci (Italy), D. Phillips (UK), R. O. Rahn (USA), E. San Román (Argentina), N. Serpone (Canada), M. Terazima (Japan). Contributors to the 3rd edition were: A. U. Acuña, W. Adam, F. Amat, D. Armesto, T. D. Z. Atvars, A. Bard, E. Bill, L. O. Björn, C. Bohne, J. Bolton, R. Bonneau, H.
    [Show full text]
  • Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems Nathan Mitchell East Tennessee State University
    East Tennessee State University Digital Commons @ East Tennessee State University Electronic Theses and Dissertations Student Works 5-2018 Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems Nathan Mitchell East Tennessee State University Follow this and additional works at: https://dc.etsu.edu/etd Part of the Analytical Chemistry Commons Recommended Citation Mitchell, Nathan, "Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems" (2018). Electronic Theses and Dissertations. Paper 3430. https://dc.etsu.edu/etd/3430 This Thesis - Open Access is brought to you for free and open access by the Student Works at Digital Commons @ East Tennessee State University. It has been accepted for inclusion in Electronic Theses and Dissertations by an authorized administrator of Digital Commons @ East Tennessee State University. For more information, please contact [email protected]. Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems ________________________ A thesis presented to the faculty of the Department of Chemistry East Tennessee State University In partial fulfillment of the requirements for the degree Master of Science in Chemistry ______________________ by Nathan Mitchell May 2018 _____________________ Dr. Dane Scott, Chair Dr. Greg Bishop Dr. Marina Roginskaya Keywords: Thermodynamic Analysis, Hydrolysis, Linear Solvent Energy Relationships, Cosolvent Systems, Acetonitrile ABSTRACT Eyring Activation Energy Analysis of Acetic Anhydride Hydrolysis in Acetonitrile Cosolvent Systems by Nathan Mitchell Acetic anhydride hydrolysis in water is considered a standard reaction for investigating activation energy parameters using cosolvents. Hydrolysis in water/acetonitrile cosolvent is monitored by measuring pH vs. time at temperatures from 15.0 to 40.0 °C and mole fraction of water from 1 to 0.750.
    [Show full text]
  • Reaction Rates: Chemical Kinetics
    Chemical Kinetics Reaction Rates: Reaction Rate: The change in the concentration of a reactant or a product with time (M/s). Reactant → Products A → B change in number of moles of B Average rate = change in time ∆()moles of B ∆[B] = = ∆t ∆t ∆[A] Since reactants go away with time: Rate=− ∆t 1 Consider the decomposition of N2O5 to give NO2 and O2: 2N2O5(g)→ 4NO2(g) + O2(g) reactants products decrease with increase with time time 2 From the graph looking at t = 300 to 400 s 0.0009M −61− Rate O2 ==× 9 10 Ms Why do they differ? 100s 0.0037M Rate NO ==× 3.7 10−51 Ms− Recall: 2 100s 0.0019M −51− 2N O (g)→ 4NO (g) + O (g) Rate N O ==× 1.9 10 Ms 2 5 2 2 25 100s To compare the rates one must account for the stoichiometry. 1 Rate O =×× 9 10−−61 Ms =× 9 10 −− 61 Ms 2 1 1 −51−−− 61 Rate NO2 =×× 3.7 10 Ms =× 9.2 10 Ms Now they 4 1 agree! Rate N O =×× 1.9 10−51 Ms−−− = 9.5 × 10 61Ms 25 2 Reaction Rate and Stoichiometry In general for the reaction: aA + bB → cC + dD 11∆∆∆∆[AB] [ ] 11[CD] [ ] Rate ====− − ab∆∆∆ttcdtt∆ 3 Rate Law & Reaction Order The reaction rate law expression relates the rate of a reaction to the concentrations of the reactants. Each concentration is expressed with an order (exponent). The rate constant converts the concentration expression into the correct units of rate (Ms−1). (It also has deeper significance, which will be discussed later) For the general reaction: aA+ bB → cC+ dD x and y are the reactant orders determined from experiment.
    [Show full text]
  • Eyring Equation and the Second Order Rate Law: Overcoming a Paradox
    Eyring equation and the second order rate law: Overcoming a paradox L. Bonnet∗ CNRS, Institut des Sciences Mol´eculaires, UMR 5255, 33405, Talence, France Univ. Bordeaux, Institut des Sciences Mol´eculaires, UMR 5255, 33405, Talence, France (Dated: March 8, 2016) The standard transition state theory (TST) of bimolecular reactions was recently shown to lead to a rate law in disagreement with the expected second order rate law [Bonnet L., Rayez J.-C. Int. J. Quantum Chem. 2010, 110, 2355]. An alternative derivation was proposed which allows to overcome this paradox. This derivation allows to get at the same time the good rate law and Eyring equation for the rate constant. The purpose of this paper is to provide rigorous and convincing theoretical arguments in order to strengthen these developments and improve their visibility. I. INTRODUCTION A classic result of first year chemistry courses is that for elementary bimolecular gas-phase reactions [1] of the type A + B −→ P roducts, (1) the time-evolution of the concentrations [A] and [B] is given by the second order rate law d[A] − = K[A][B], (2) dt where K is the rate constant. For reactions proceeding through a barrier along the reaction path, Eyring famous equation [2] allows the estimation of K with a considerable success for more than 80 years [3]. This formula is the central result of activated complex theory [2], nowadays called transition state theory (TST) [3–18]. Note that other researchers than Eyring made seminal contributions to the theory at about the same time [3], like Evans and Polanyi [4], Wigner [5, 6], Horiuti [7], etc..
    [Show full text]
  • Time-Temperature Superposition WHICH VARIABLES ARE TEMPERATURE DEPENDENT in the ROUSE and REPTATION MODELS?
    Time-Temperature Superposition WHICH VARIABLES ARE TEMPERATURE DEPENDENT IN THE ROUSE AND REPTATION MODELS? Rouse Relaxation Modulus: N ρ(T )RT X 2 G(t) = e−tp /λR M p=1 Rouse Relaxation Time: a2N 2ζ(T ) λ = R 6π2kT Reptation Relaxation Modulus: N 8 ρ(T )RT 1 2 X −p t/λd G(t) = 2 2 e π Me p p odd Reptation Relaxation Time: a2N 2ζ(T ) M λd = 2 π kT Me Both models have the same temperature dependence. This is hardly surprising, since reptation is just Rouse motion confined in a tube. Modulus Scale G ∼ ρ(T )T ζ(T ) Time Scale λ ∼ ∼ λ T N Since the friction factor is related to the shortest Rouse mode λN . a2ζ(T ) λ = N 6π2kT 1 Time-Temperature Superposition METHOD OF REDUCED VARIABLES All relaxation modes scale in the same way with temperature. λi(T ) = aT λi(T0) (2-116) aT is a time scale shift factor T0 is a reference temperature (aT ≡ 1 at T = T0). Gi(T0)T ρ Gi(T ) = (2-117) T0ρ0 Recall the Generalized Maxwell Model N X G(t) = Gi exp(−t/λi) (2-25) i=1 with full temperature dependences of the Rouse (and Reptation) Model N T ρ X G(t, T ) = G (T ) exp{−t/[λ (T )a ]} (2-118) T ρ i 0 i 0 T 0 0 i=1 We simplify this by defining reduced variables that are independent of temperature. T ρ G (t) ≡ G(t, T ) 0 0 (2-119) r T ρ t tr ≡ (2-120) aT N X Gr(tr) = Gi(T0) exp[−tr/λi(T0)] (2-118) i=1 Plot of Gr as a function of tr is a universal curve independent of tem- perature.
    [Show full text]
  • A First Course on Kinetics and Reaction Engineering Example 4.6
    A First Course on Kinetics and Reaction Engineering Example 4.6 Problem Purpose This example illustrates the use of an Arrhenius plot to determine the best values of a pre- exponential factor and an activation energy. Problem Statement Kinetic studies were performed at a number of different temperatures to find the value of a second order rate coefficient at each of the temperatures. The results are given in the table below. Determine whether the temperature dependence of this rate coefficient is consistent with the Arrhenius equation, and find the best values for the pre-exponential factor and the activation energy. Temperature Rate Coefficient (°C) (L mol-1 min-1) 10 2.63 x 10-4 22 4.78 x 10-4 40 1.52 x 10-3 54 4.18 x 10-3 65 9.07 x 10-3 78 2.14 x 10-2 89 4.2 x 10-2 103 9.42 x 10-2 Problem Analysis This problem clearly involves the use of the Arrhenius expression for the temperature dependence of a rate coefficient. The Arrhenius expression contains two unknown constants, the pre-exponential factor and the activation energy. Here we are given the value of the rate coefficient at eight different temperatures. If we substituted each of those eight data points into the Arrhenius expression, we would have eight equations in two unknowns. Unless the data were “made up” using the Arrhenius expression, there won’t be a single value of the pre-exponential factor and a single value of the activation energy that together satisfy the eight equations.
    [Show full text]
  • Enthalpy and Free Energy of Reaction
    KINETICS AND THERMODYNAMICS OF REACTIONS Key words: Enthalpy, entropy, Gibbs free energy, heat of reaction, energy of activation, rate of reaction, rate law, energy profiles, order and molecularity, catalysts INTRODUCTION This module offers a very preliminary detail of basic thermodynamics. Emphasis is given on the commonly used terms such as free energy of a reaction, rate of a reaction, multi-step reactions, intermediates, transition states etc., FIRST LAW OF THERMODYNAMICS. o Law of conservation of energy. States that, • Energy can be neither created nor destroyed. • Total energy of the universe remains constant. • Energy can be converted from one form to another form. eg. Combustion of octane (petrol). 2 C8H18(l) + 25 O2(g) CO2(g) + 18 H2O(g) Conversion of potential energy into thermal energy. → 16 + 10.86 KJ/mol . ESSENTIAL FACTORS FOR REACTION. For a reaction to progress. • The equilibrium must favor the products- • Thermodynamics(energy difference between reactant and product) should be favorable • Reaction rate must be fast enough to notice product formation in a reasonable period. • Kinetics( rate of reaction) ESSENTIAL TERMS OF THERMODYNAMICS. Thermodynamics. Predicts whether the reaction is thermally favorable. The energy difference between the final products and reactants are taken as the guiding principle. The equilibrium will be in favor of products when the product energy is lower. Molecule with lowered energy posses enhanced stability. Essential terms o Free energy change (∆G) – Overall free energy difference between the reactant and the product o Enthalpy (∆H) – Heat content of a system under a given pressure. o Entropy (∆S) – The energy of disorderness, not available for work in a thermodynamic process of a system.
    [Show full text]
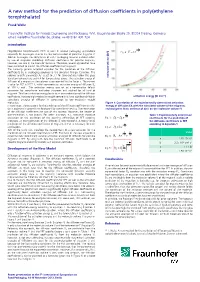
  • A New Method for the Prediction of Diffusion Coefficients in Poly(Ethylene Terephthalate)
    A new method for the prediction of diffusion coefficients in poly(ethylene terephthalate) Frank Welle Fraunhofer Institute for Process Engineering and Packaging (IVV), Giggenhauser Straße 35, 85354 Freising, Germany, email: [email protected], phone: ++49 8161 491 724 Introduction E d A R Poly(ethylene terephthalate) (PET) is used in several packaging applications ] 3 Eq. 4: V c e especially for beverages. Due to the low concentration of potential migrants in food or beverages, the compliance of a PET packaging material is shown often by use of migration modelling. Diffusion coefficients for possible migrants, however, are rare in the scientific literature. Therefore, several approaches have been published to predict the diffusion coefficients of migrants. The currently general accepted equation for the prediction of the diffusion coefficients DP in packaging polymers is the so-called Piringer Equation. The polymer specific parameter AP' is set to 3.1 for temperatures below the glass transition temperature and 6.4 for temperatures above. The activation energy of [Å molecular volume diffusion of a migrant in the polymer is represented by the factor . The current value for PET is 1577 K, which represents an activation energy of diffusion EA of 100 kJ mol-1. This activation energy was set as a conservative default parameter for compliance evaluation purposes and applied for all kind of migrants. This fixed activation energy leads to an over-estimation of the diffusion coefficients, because high molecular weight compounds have significantly higher activation energy [kJ mol-1] activations energies of diffusion in comparison to low molecular weight molecules. Figure 1: Correlation of the experimentally determined activation In conclusion, the equations for the prediction of the diffusion coefficients in PET energy of diffusion EA with the calculated volume of the migrants, (or in polymers in general) are developed for compliance testing.
    [Show full text]
  • Reaction Rates and Temperature; Arrhenius Theory Arrhenius Theory
    Reaction Rates and Temperature; Arrhenius Theory CHEM 102 T. Hughbanks Arrhenius Theory −Ea Ae RT k = k is the rate constant! T is the temperature in K! E is the activation energy! R is the ideal-gas constant a (8.314 J/Kmol)! In addition to carrying the units of the rate constant, “A” relates to the frequency of collisions and the orientation of a favorable collision probability! Both A and Ea are specific to a given reaction. ! In order for the reaction to proceed, the reactants ! must posses enough energy to surmount a Eact! reaction barrier. ! "HRXN! PotentialEnergy Reaction Progress! Energy profile for a reaction “activated complex” Rate-determining Ea Quantity reactants Energy ∆E rxn products Thermodynamic Quantity “Reaction Coordinate” The reverse direction... “activated complex” Rate-determining for reverse reaction E (reverse) “products” a Energy ∆E rxn “reactants” Thermodynamic Quantity “Reaction Coordinate” Ea, The Activation Energy Energy of activation for forward reaction:" Ea = Etransition state - Ereactants A reaction can’t proceed unless reactants possess enough energy to give Ea. ∆E, the thermodynamic quantity, tells us about the net reaction. The activation energy, Ea , must be available in the surroundings for the reaction to proceed at a measurable rate. The temperature for a system of particles is described by a distribution of energies. At higher temps, more particles have enough energy to go over the barrier. E > Ea! Since the probability of a E < Ea! molecule reacting increases, the rate increases. The orientation of a molecule during collision can have a profound effect on whether or not a reaction occurs.
    [Show full text]