DOCSLIB.ORG

Nuclear Astrophysics and Exotics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Nuclear Astrophysics and Exotics Nuclear Astrophysics and Exotics Artemis Spyrou Michigan State University Artemis Spyrou, Belfast 2017, 1 Overview Lecture 1: Intro to Nuclear Astrophysics - reactions Lecture 2: How to measure cross sections + activity Lecture 3: Nuclear structure for astrophysics Lecture 4: Exotic phenomena close to the drip lines Artemis Spyrou, Belfast 2017, 2 Abundances From M. Wiescher, JINA web Artemis Spyrou, Belfast 2017, 3 Nucleosynthesis paths Z 56Fe Stellar burning pp chain N Artemis Spyrou, Belfast 2017, 4 Paths beyond Iron Artemis Spyrou, Belfast 2017, 5 Nuclear Astrophysics Connections Numerical approximaons Astrophysical Nuclear Input condions Stellar modeling • Solar system abundances • Stellar observaons – Abundances Compare to • Meteori:c samples Observaons • Light output / Energy produc:on • Time scales Artemis Spyrou, Belfast 2017, 6 Nuclear input: What do we need? o Basic nuclear properties • Mass • Binding energy • Half life • Level structure • Angular • Nuclear radius/shape Momentum Artemis Spyrou, Belfast 2017, 7 Nuclear Input νp-process • Close to proton drip line • Masses, T1/2 mostly known • Most important (p,n) reactions rp-process r-process • Close to proton drip line 56Fe • Masses, T1/2 mostly known • Far from stability • Proton capture reactions • Most properties not known • Masses • T1/2 • Pn Burning • Neutron captures p-process • Nuclear reactions • Resonance properties • Close to stability i-process • Masses, T1/2 known s-process • Between s and r • γ-induced reaction rates • Along stability • Mass, T1/2 known • Most properties known • Missing neutron captures • Missing neutron captures Artemis Spyrou, Belfast 2017, 8 Nuclear Reactions in Stars Main focus on capture reactions Artemis Spyrou, Belfast 2017, 9 Y X υ r = NX NYυσ(υ) ∞ r N N f(υ)σ(υ)υdυ f (υ) = X Y ∫ 0 r: reaction rate Nx, Ny: number of particles υ:velocity r ∞ σ(υ): reaction cross section at υ συ = = f(υ)σ (υ)υdυ N N ∫ f(υ): velocity distribution X Y 0 <συ>: reaction rate per particle pair Rolfs and Rodney, “Cauldrons in the cosmos” Artemis Spyrou, Belfast 2017, 10 Maxwell – Boltzmann distribution 2 ⎛ mυ ⎞ 0.5 3/ 2 ⎜ ⎟ ⎜ − ⎟ 2 ⎛ m ⎞ ⎝ 2kT ⎠ f(υ) = 4πυ ⎜ ⎟ e 0.4 (E) 2πkT φ ⎝ ⎠ 0.3 0.2 Distribution Distribution 0.1 3/ 2 ⎛ E ⎞ ⎜ − ⎟ 2 ⎛ 1 ⎞ 1/ 2 kT φ(E) = ⎜ ⎟ E e⎝ ⎠ 0.0 π ⎝ kT ⎠ 0kT 2kT 4kT 6kT 8kT 10kT 12kT 14kT Energy E 1/2 ! E $ ! 8 $ 1 ∞ #− & (E)Ee" kT %dE συ = # & 3/2 ∫ σ "πµ % (kT) 0 Rolfs and Rodney, “Cauldrons in the cosmos” Artemis Spyrou, Belfast 2017, 11 Tunnel Effect – S-factor 2 Coulomb barrier ψ (Rn ) P = 2 ψ (Rc ) projecle Tunneling probability -> R n Rc Distance r increasing with energy Poten:al V(r) Nuclear radius Artemis Spyrou, Belfast 2017, 12 Cross section has two components: 1. Interaction between particles (pure nuclear) 2. The Coulomb force Astrophysical S-factor 1 (−2πη) σ (E) = e S(E) Contains all the pure nuclear E properties Z Z e2 η: Sommerfeld parameter η = 1 2 !υ Rolfs and Rodney, “Cauldrons in the cosmos” Artemis Spyrou, Belfast 2017, 12 Astrophysical region S-factor σ(Ε) Coulomb Barrier Log Scale Cross Section Extrapolation The dangers of extrapolation S(E) factor Linear Scale Energy E Artemis Spyrou, Belfast 2017, 13 Gamow Window Maxwell – Boltzmann distribu:on Tunneling probability ⎛ E ⎞ # & ∝ exp⎜− ⎟ EC ⎝ kT ⎠ ∝ exp%− ( $ E ' Gamow peak ΔE0 Relative probability E0 Energy Artemis Spyrou, Belfast 2017, 14 Gamow Window • Charged particles Burning: T= 0.01 – 0.1 GK o (p,γ): Ep= 0.02 – 0.2MeV Standard approximation o (α,γ): Eα= 0.05 -0.5 MeV p process: T= 1.8 – 3.3 GK 2 2 2 1/3 E0 = 0.12204(Z1 Z2 µT9 ) o (p,γ): Ep= 1 – 5 MeV [in MeV] o (α,γ): Eα= 4 -12 MeV E 0.237(Z 2Z 2 T 5 )1/6 Δ 0 = 1 2 µ 9 rp process: T= 1.1 – 1.3 GK o (p,γ): E = 0.8 – 2 MeV ΔE p Window: E + 0 νp process: T= 1.5 – 3.0 GK 0 2 o (p,γ): Ep= 1 – 4 MeV • Neutrons No Coulomb barrier, angular momentum 1 s process: T~ 0.3GK Eeff = 0.172T9 (ℓ + ) 2 o (n,γ): En= 25 - 75 keV [in MeV] i process: T= 0.1-0.3GK 1 o (n,γ): Ep= 10 – 75 MeV ΔEeff = 0.194T9 ℓ + 2 r process: T= 0.1 – 2.0 GK ΔEeff Window: E + o (n,γ): Ep= 10 – 500 keV eff 2 Rauscher, PRC 81 (2010) 045807 Kadonis.org : Gamow Calculator Artemis Spyrou, Belfast 2017, 15 Nuclear input: What do we need? o Nuclear reactions/Astrophysical reaction rates * a A B B Radiative capture reactions Incoming channel + → → +γ Resonant Statistical Direct A A A Q Q Q B B B Artemis Spyrou, Belfast 2017, 16 o Example: 24Mg(p,γ)25Al Marialuisa Aliotta, University of Edinburgh 11th Euro Summer School on Exotic Beams Artemis Spyrou, Belfast 2017, 17 Nuclear input: What do we need? o Nuclear reactions/Astrophysical reaction rates a + A → B* → B +γ Prompt Outgoing channel or other particle channels (Competing channels) n γ B-1n Delayed A Q β B n Τ1/2 γ C-1n C Artemis Spyrou, Belfast 2017, 18 Experiment Accelerator Facilities Artemis Spyrou, Belfast 2017, 19 Facilities Stable beam facilities (Intro Physics) • Van de Graaff (single-ended or tandem) • Cyclotrons • LINACS Artemis Spyrou, Belfast 2017, 20 Basic Components Analyzing magnet Accelerator Ion sources Beam Lines 5MV tandem accelerator @ Institute of Nuclear Physics, “Demokritos”, Athens, Greece Artemis Spyrou, Belfast 2017, 21 Radioactive Beams • Fragmenta0on: NSCL/FRIB, GSI/FAIR, RIKEN, … Target Fast RIB Stable beam Fragmentaon Separaon • Isotope Separaon On-Line (ISOL): TRIUMF, SPIRAL, ISOLDE, … Target Extrac:on Stable beam RIB Separaon Reacceleraon • Fission source: CARIBU/ANL Fission source Separaon Acceleraon RIB Extrac:on • Low energy reac0ons: ANL, FSU, Texas A&M, Notre Dame, … Target Low energy RIB Stable beam Reac:on Separaon? Artemis Spyrou, Belfast 2017, 22 NSCL@MSU • Naonal Superconduc0ng Cyclotron Laboratory “Stopped beam area” Gas Stopper ReAccelerator Facility K500 Cyclotron S800 Spectrograph A1900 Fragment Separator K1200 Cyclotron Artemis Spyrou, Belfast 2017, 23 Coupled Cyclotron Facility Example: 86Kr → 78Ni K500 ion sources coupling 86Kr14+, line 12 MeV/u K1200 A1900 focal plane Δp/p = 5% producon transmission stripping 86Kr34+, target foil of 65% of the 140 MeV/u produced 78Ni wedge fragment yield aer target fragment yield aer wedge fragment yield at focal plane Artemis Spyrou, Belfast 2017, 24 Neutron Facilities Time-of-Flight: e.g. nTOF@CERN, LANSCE@ Los Alamos, IRMM@Geel, Belgium, etc • High energy protons on heavy target, broad energy distribu:on, pulsed beam. Reac0on-based, quasi-monoenergec: Any low energy facility 2 2 3 • Reac:ons: H( H,n) He – Q= 3.3 MeV - En= 2.5 MeV 3 2 4 H( H,n) He – Q= 17.6 MeV - En = 14.1 MeV 7 7 Li(p,n) Be – Q= - 1.64 MeV – En=? – How can you get 25 keV? … Artemis Spyrou, Belfast 2017, 25 In the Laboratory Number of reactions • Yield of reaction: Y = Number of beam particles Yield of reaction N • Cross section: σ = = R Number of target particles Nb ⋅ NT To measure a cross section you need three things: 1. Number of target particles (NT) !!! 2. Number of beam particles (Nb) !!! 3. Number of reactions (NR) !!! Artemis Spyrou, Belfast 2017, 26 Number of target particles 1 • Rutherford backscattering 92 ΔΕ0 Mo target 0 Mo Ed = 1.35 MeV ΔΕ - experiment 0 0 Ε Ε Beam simulation ο 170 Ε1 Ε1-ΔΕ Al backing 1 Si detector # events ΔΕ # events 1 Energy (keV) Ε -ΔΕ Ε Ε 1 1 1 o Simulation with SIMNRA o Known detector geometry N : Avogadro number N Aξ A o Known cross section NT = A: Atomic mass A ξ: target thickness in g/cm2 o Free parameter: target thickness/composition Artemis Spyrou, Belfast 2017, 27 Tools 1 Si surface barrier detector – Semi-conductor hp://nsspi.tamu.edu/nssep/courses/basic-radiaon-detec:on/ semiconductor-detectors/introduc:on/introduc:on Artemis Spyrou, Belfast 2017, 28 Number of target particles 1 • X-ray Fluorescence (XRF) M L K M L K X-ray detector # events Energy (keV) Artemis Spyrou, Belfast 2017, 29 Tools 1 SiLi detector – Semi-conductor X-ray tube • Cooling • Addition of Li helps remove impurities hmp://nau.edu/cefns/labs/electron-microprobe/glg-510-class-notes/ detec:on-of-signals/ hmp://www.schoolphysics.co.uk/age16-19/Medical%20physics/text/ X_rays/index.html Artemis Spyrou, Belfast 2017, 30 Number of target particles 1 • Particle energy loss ΔΕ0 0 ΔΕ - 0 0 Ε α α Ε source source Si detector Si detector # events Ε Ε0-ΔΕ0 Ε0 o Many other techniques like resonance measurement, use of spectrometer or recoil separator, use a reaction, etc o If radioactive sample: activity from decay Artemis Spyrou, Belfast 2017, 31 In the Laboratory Number of reactions • Yield of reaction: Y = Number of beam particles Yield of reaction N • Cross section: σ = = R Number of target particles Nb ⋅ NT To measure a cross section you need three things: 1. Number of target particles (NT) !!! 2. Number of beam particles (Nb) !!! 3. Number of reactions (NR) !!! Artemis Spyrou, Belfast 2017, 32 Number of beam particles 2 • High beam intensities: measure deposited charge Collimator 1 Collimator 2 Target beam detector A Ammeter/ Current integrator e.g. 1H+ beam: each beam particle deposits 1.6 x 10-19 Cb (e- charge) 84Kr27+ beam: each beam particle deposits 27 x 1.6 x 10-19 Cb Artemis Spyrou, Belfast 2017, 33 Number of beam particles 2 • High beam intensities: measure deposited charge Collimator 1 Collimator 2 - Target e e- beam detector - - e - e e- e A Ammeter/ Current integrator Artemis Spyrou, Belfast 2017, 34 Number of beam particles 2 • High beam intensities: measure deposited charge Collimator 1 Collimator 2 - Target e- - e e- beam e detector - - e- e- e - e e- e- e e- A Ammeter/ Current integrator +- Beam: positive charge +1e + +-+- Measurement 1: +1e +- Measurement 2: +2e = false +- +- +- How do we fix it? Artemis Spyrou, Belfast 2017, 35 Number of beam particles 2 • Low beam intensities: measure each particle in detector 1.
Load more

Recommended publications
  • Nuclear Physics
    Nuclear Physics Overview One of the enduring mysteries of the universe is the nature of matter—what are its basic constituents and how do they interact to form the properties we observe? The largest contribution by far to the mass of the visible matter we are familiar with comes from protons and heavier nuclei. The mission of the Nuclear Physics (NP) program is to discover, explore, and understand all forms of nuclear matter. Although the fundamental particles that compose nuclear matter—quarks and gluons—are themselves relatively well understood, exactly how they interact and combine to form the different types of matter observed in the universe today and during its evolution remains largely unknown. Nuclear physicists seek to understand not just the familiar forms of matter we see around us, but also exotic forms such as those that existed in the first moments after the Big Bang and that exist today inside neutron stars, and to understand why matter takes on the specific forms now observed in nature. Nuclear physics addresses three broad, yet tightly interrelated, scientific thrusts: Quantum Chromodynamics (QCD); Nuclei and Nuclear Astrophysics; and Fundamental Symmetries: . QCD seeks to develop a complete understanding of how the fundamental particles that compose nuclear matter, the quarks and gluons, assemble themselves into composite nuclear particles such as protons and neutrons, how nuclear forces arise between these composite particles that lead to nuclei, and how novel forms of bulk, strongly interacting matter behave, such as the quark-gluon plasma that formed in the early universe. Nuclei and Nuclear Astrophysics seeks to understand how protons and neutrons combine to form atomic nuclei, including some now being observed for the first time, and how these nuclei have arisen during the 13.8 billion years since the birth of the cosmos.
    [Show full text]
  • The R-Process Nucleosynthesis and Related Challenges
    EPJ Web of Conferences 165, 01025 (2017) DOI: 10.1051/epjconf/201716501025 NPA8 2017 The r-process nucleosynthesis and related challenges Stephane Goriely1,, Andreas Bauswein2, Hans-Thomas Janka3, Oliver Just4, and Else Pllumbi3 1Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles, CP 226, 1050 Brussels, Belgium 2Heidelberger Institut fr¨ Theoretische Studien, Schloss-Wolfsbrunnenweg 35, 69118 Heidelberg, Germany 3Max-Planck-Institut für Astrophysik, Postfach 1317, 85741 Garching, Germany 4Astrophysical Big Bang Laboratory, RIKEN, 2-1 Hirosawa, Wako, Saitama, 351-0198, Japan Abstract. The rapid neutron-capture process, or r-process, is known to be of fundamental importance for explaining the origin of approximately half of the A > 60 stable nuclei observed in nature. Recently, special attention has been paid to neutron star (NS) mergers following the confirmation by hydrodynamic simulations that a non-negligible amount of matter can be ejected and by nucleosynthesis calculations combined with the predicted astrophysical event rate that such a site can account for the majority of r-material in our Galaxy. We show here that the combined contribution of both the dynamical (prompt) ejecta expelled during binary NS or NS-black hole (BH) mergers and the neutrino and viscously driven outflows generated during the post-merger remnant evolution of relic BH-torus systems can lead to the production of r-process elements from mass number A > 90 up to actinides. The corresponding abundance distribution is found to reproduce the∼ solar distribution extremely well. It can also account for the elemental distributions observed in low-metallicity stars. However, major uncertainties still affect our under- standing of the composition of the ejected matter.
    [Show full text]
  • Status and Perspectives of the Neutron Time-Of-Flight Facility N TOF at CERN
    Status and perspectives of the neutron time-of-flight facility n_TOF at CERN E. Chiaveri on behalf of the n_TOF Collaboration ([email protected]) Since the start of its operation in 2001, based on an idea of Prof. Carlo Rubbia[1], the neutron time-of-flight facility of CERN, n_TOF, has become one of the most forefront neutron facilities in the world for wide-energy spectrum neutron cross section measurements. Thanks to the combination of excellent neutron energy resolution and high instantaneous neutron flux available in the two experimental areas, the second of which has been constructed in 2014, n_TOF is providing a wealth of new data on neutron-induced reactions of interest for nuclear astrophysics, advanced nuclear technologies and medical applications. The unique features of the facility will continue to be exploited in the future, to perform challenging new measurements addressing the still open issues and long-standing quests in the field of neutron physics. In this document the main characteristics of the n_TOF facility and their relevance for neutron studies in the different areas of research will be outlined, addressing the possible future contribution of n_TOF in the fields of nuclear astrophysics, nuclear technologies and medical applications. In addition, the future perspectives of the facility will be described including the upgrade of the spallation target. 1 Introduction Neutron-induced reactions play a fundamental role for a number of research fields, from the origin of chemical elements in stars, to basic nuclear physics, to applications in advanced nuclear technology for energy, dosimetry, medicine and space science [1]. Thanks to the time-of-flight technique coupled with the characteristics of the CERN n_TOF beam-lines and neutron source, reaction cross-sections can be measured with a very high energy-resolution and in a broad neutron energy range from thermal up to GeV.
    [Show full text]
  • Simulating Nuclear and Astrophysical Processes in the Lab. Artemis Spyrou
    The nuclear Physics of exploding stars: simulating nuclear and astrophysical processes in the lab. Artemis Spyrou [email protected] @ArtemisSpyrou • Nuclear Astrophysics • Nucleosynthesis • Nuclear Physics Input • Sample project description Figure Credit: Erin O’Donnel, NSCL Artemis Spyrou, September 2018,2017, Slide 1 Elements in nature 1 2 H He 3 4 5 6 7 8 9 10 Li Be B C N O F Ne 11 12 13 14 15 16 17 18 Na Mg Al Si P S Cl Ar 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe 55 56 57 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 Cs Ba La Hf Ta W Re Os Ir Pt Au Hg Tl Pd Bi Po At Rn 87 88 89 104 105 106 107 108 109 110 Fr Ra Ac Rf Ha Sg Bh Hs Mt Ds … 58 59 60 61 62 63 64 65 66 67 68 69 70 71 Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu 90 91 92 93 94 95 96 97 98 99 100 101 102 103 Th Pa U Np Pu Am Cm Bk Cf Es Fm Md No Lr Artemis Spyrou, September 2018,2017, Slide 2 Elements in nature 1 2 H He 3 Li BANG Artemis Spyrou, September 2018,2017, Slide 3 Elements in nature 1 The rest… made in stars!!! 2 H He 3 4 5 6 7 8 9 10 Li Be B C N O F Ne 11 12 13 14 15 16 17 18 Na Mg Al Si P S Cl Ar 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 Ag Cd I Rb Sr BANGY Zr Nb Mo Tc Ru Rh Pd In Sn Sb Te Xe 55 56 57 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 Cs Ba La Hf Ta W Re Os Ir Pt Au Hg
    [Show full text]
  • White Paper on Nuclear Astrophysics and Low Energy Nuclear Physics
    WHITE PAPER ON NUCLEAR ASTROPHYSICS AND LOW ENERGY NUCLEAR PHYSICS PART 1: NUCLEAR ASTROPHYSICS FEBRUARY 2016 NUCLEAR ASTROPHYSICS & LOW ENERGY NUCLEAR PHYSICS 1 Edited by: Hendrik Schatz and Michael Wiescher Layout and design: Erin O’Donnell, NSCL, Michigan State University Individual sections have been edited by the section conveners: Almudena Arcones, Dan Bardayan, Lee Bernstein, Jeffrey Blackmon, Edward Brown, Carl Brune, Art Champagne, Alessandro Chieffi, Aaron Couture, Roland Diehl, Jutta Escher, Brian Fields, Carla Froehlich, Falk Herwig, Raphael Hix, Christian Iliadis, Bill Lynch, Gail McLaughlin, Bronson Messer, Bradley Meyer, Filomena Nunes, Brian O'Shea, Madappa Prakash, Boris Pritychenko, Sanjay Reddy, Ernst Rehm, Grisha Rogachev, Bob Ruthledge, Michael Smith, Andrew Steiner, Tod Strohmayer, Frank Timmes, Remco Zegers, Mike Zingale NUCLEAR ASTROPHYSICS & LOW ENERGY NUCLEAR PHYSICS 2 ABSTRACT This white paper informs the nuclear astrophysics community and funding agencies about the scientific directions and priorities of the field and provides input from this community for the 2015 Nuclear Science Long Range Plan. It summarizes the outcome of the nuclear astrophysics town meeting that was held on August 21-23, 2014 in College Station at the campus of Texas A&M University in preparation of the NSAC Nuclear Science Long Range Plan. It also reflects the outcome of an earlier town meeting of the nuclear astrophysics community organized by the Joint Institute for Nuclear Astrophysics (JINA) on October 9- 10, 2012 Detroit, Michigan, with the purpose of developing a vision for nuclear astrophysics in light of the recent NRC decadal surveys in nuclear physics (NP2010) and astronomy (ASTRO2010). The white paper is furthermore informed by the town meeting of the Association of Research at University Nuclear Accelerators (ARUNA) that took place at the University of Notre Dame on June 12-13, 2014.
    [Show full text]
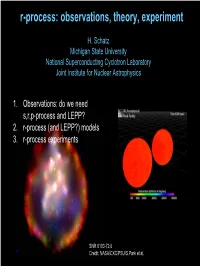
  • R-Process: Observations, Theory, Experiment
    r-process: observations, theory, experiment H. Schatz Michigan State University National Superconducting Cyclotron Laboratory Joint Institute for Nuclear Astrophysics 1. Observations: do we need s,r,p-process and LEPP? 2. r-process (and LEPP?) models 3. r-process experiments SNR 0103-72.6 Credit: NASA/CXC/PSU/S.Park et al. Origin of the heavy elements in the solar system s-process: secondary • nuclei can be studied Æ reliable calculations • site identified • understood? Not quite … r-process: primary • most nuclei out of reach • site unknown p-process: secondary (except for νp-process) Æ Look for metal poor`stars (Pagel, Fig 6.8) To learn about the r-process Heavy elements in Metal Poor Halo Stars CS22892-052 (Sneden et al. 2003, Cowan) 2 1 + solar r CS 22892-052 ) H / X CS22892-052 ( g o red (K) giant oldl stars - formed before e located in halo Galaxyc was mixed n distance: 4.7 kpc theya preserve local d mass ~0.8 M_sol n pollutionu from individual b [Fe/H]= −3.0 nucleosynthesisa events [Dy/Fe]= +1.7 recall: element number[X/Y]=log(X/Y)-log(X/Y)solar What does it mean: for heavy r-process? For light r-process? • stellar abundances show r-process • process is not universal • process is universal • or second process exists (not visible in this star) Conclusions depend on s-process Look at residuals: Star – solar r Solar – s-process – p-process s-processSimmerer from Simmerer (Cowan et etal.) al. /Lodders (Cowan et al.) s-processTravaglio/Lodders from Travaglio et al. -0.50 -0.50 -1.00 -1.00 -1.50 -1.50 log e log e -2.00 -2.00 -2.50 -2.50 30 40 50 60 70 80 90 30 40 50 60 70 80 90 Element number Element number ÆÆNeedNeed reliable reliable s-process s-process (models (models and and nu nuclearclear data, data, incl.
    [Show full text]
  • Arxiv:1901.01410V3 [Astro-Ph.HE] 1 Feb 2021 Mental Information Is Available, and One Has to Rely Strongly on Theoretical Predictions for Nuclear Properties
    Origin of the heaviest elements: The rapid neutron-capture process John J. Cowan∗ HLD Department of Physics and Astronomy, University of Oklahoma, 440 W. Brooks St., Norman, OK 73019, USA Christopher Snedeny Department of Astronomy, University of Texas, 2515 Speedway, Austin, TX 78712-1205, USA James E. Lawlerz Physics Department, University of Wisconsin-Madison, 1150 University Avenue, Madison, WI 53706-1390, USA Ani Aprahamianx and Michael Wiescher{ Department of Physics and Joint Institute for Nuclear Astrophysics, University of Notre Dame, 225 Nieuwland Science Hall, Notre Dame, IN 46556, USA Karlheinz Langanke∗∗ GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany and Institut f¨urKernphysik (Theoriezentrum), Fachbereich Physik, Technische Universit¨atDarmstadt, Schlossgartenstraße 2, 64298 Darmstadt, Germany Gabriel Mart´ınez-Pinedoyy GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany; Institut f¨urKernphysik (Theoriezentrum), Fachbereich Physik, Technische Universit¨atDarmstadt, Schlossgartenstraße 2, 64298 Darmstadt, Germany; and Helmholtz Forschungsakademie Hessen f¨urFAIR, GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany Friedrich-Karl Thielemannzz Department of Physics, University of Basel, Klingelbergstrasse 82, 4056 Basel, Switzerland and GSI Helmholtzzentrum f¨urSchwerionenforschung, Planckstraße 1, 64291 Darmstadt, Germany (Dated: February 2, 2021) The production of about half of the heavy elements found in nature is assigned to a spe- cific astrophysical nucleosynthesis process: the rapid neutron capture process (r-process). Although this idea has been postulated more than six decades ago, the full understand- ing faces two types of uncertainties/open questions: (a) The nucleosynthesis path in the nuclear chart runs close to the neutron-drip line, where presently only limited experi- arXiv:1901.01410v3 [astro-ph.HE] 1 Feb 2021 mental information is available, and one has to rely strongly on theoretical predictions for nuclear properties.
    [Show full text]
  • Investigations of Nuclear Decay Half-Lives Relevant to Nuclear Astrophysics
    DE TTK 1949 Investigations of nuclear decay half-lives relevant to nuclear astrophysics PhD Thesis Egyetemi doktori (PhD) ´ertekez´es J´anos Farkas Supervisor / T´emavezet˝o Dr. Zsolt F¨ul¨op University of Debrecen PhD School in Physics Debreceni Egyetem Term´eszettudom´anyi Doktori Tan´acs Fizikai Tudom´anyok Doktori Iskol´aja Debrecen 2011 Prepared at the University of Debrecen PhD School in Physics and the Institute of Nuclear Research of the Hungarian Academy of Sciences (ATOMKI) K´esz¨ult a Debreceni Egyetem Fizikai Tudom´anyok Doktori Iskol´aj´anak magfizikai programja keret´eben a Magyar Tudom´anyos Akad´emia Atommagkutat´o Int´ezet´eben (ATOMKI) Ezen ´ertekez´est a Debreceni Egyetem Term´eszettudom´anyi Doktori Tan´acs Fizikai Tudom´anyok Doktori Iskol´aja magfizika programja keret´eben k´esz´ıtettem a Debreceni Egyetem term´eszettudom´anyi doktori (PhD) fokozat´anak elnyer´ese c´elj´ab´ol. Debrecen, 2011. Farkas J´anos Tan´us´ıtom, hogy Farkas J´anos doktorjel¨olt a 2010/11-es tan´evben a fent megnevezett doktori iskola magfizika programj´anak keret´eben ir´any´ıt´asommal v´egezte munk´aj´at. Az ´ertekez´esben foglalt eredm´e- nyekhez a jel¨olt ¨on´all´oalkot´otev´ekenys´eg´evel meghat´aroz´oan hozz´a- j´arult. Az ´ertekez´es elfogad´as´at javaslom. Debrecen, 2011. Dr. F¨ul¨op Zsolt t´emavezet˝o Investigations of nuclear decay half-lives relevant to nuclear astrophysics Ertekez´es´ a doktori (PhD) fokozat megszerz´ese ´erdek´eben a fizika tudom´any´agban ´Irta: Farkas J´anos, okleveles fizikus ´es programtervez˝omatematikus K´esz¨ult a Debreceni Egyetem Fizikai Tudom´anyok Doktori Iskol´aja magfizika programja keret´eben T´emavezet˝o: Dr.
    [Show full text]
  • Low-Energy Nuclear Physics Part 2: Low-Energy Nuclear Physics
    BNL-113453-2017-JA White paper on nuclear astrophysics and low-energy nuclear physics Part 2: Low-energy nuclear physics Mark A. Riley, Charlotte Elster, Joe Carlson, Michael P. Carpenter, Richard Casten, Paul Fallon, Alexandra Gade, Carl Gross, Gaute Hagen, Anna C. Hayes, Douglas W. Higinbotham, Calvin R. Howell, Charles J. Horowitz, Kate L. Jones, Filip G. Kondev, Suzanne Lapi, Augusto Macchiavelli, Elizabeth A. McCutchen, Joe Natowitz, Witold Nazarewicz, Thomas Papenbrock, Sanjay Reddy, Martin J. Savage, Guy Savard, Bradley M. Sherrill, Lee G. Sobotka, Mark A. Stoyer, M. Betty Tsang, Kai Vetter, Ingo Wiedenhoever, Alan H. Wuosmaa, Sherry Yennello Submitted to Progress in Particle and Nuclear Physics January 13, 2017 National Nuclear Data Center Brookhaven National Laboratory U.S. Department of Energy USDOE Office of Science (SC), Nuclear Physics (NP) (SC-26) Notice: This manuscript has been authored by employees of Brookhaven Science Associates, LLC under Contract No.DE-SC0012704 with the U.S. Department of Energy. The publisher by accepting the manuscript for publication acknowledges that the United States Government retains a non-exclusive, paid-up, irrevocable, world-wide license to publish or reproduce the published form of this manuscript, or allow others to do so, for United States Government purposes. DISCLAIMER This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, nor any of their contractors, subcontractors, or their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or any third party’s use or the results of such use of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights.
    [Show full text]
  • The U.S. Nuclear Reaction Data Network
    BNL-NCS-63006 INFORMAL REPORT LIMITED DISTRIBUTION THE U.S. NUCLEAR REACTION DATA NETWORK Summary of the First Meeting held at the Colorado School of Mines Golden, Colorado March 13 & 14,1996 Assembled by M.R. Bhat National Nuclear Data Center Secretariat Department of Advanced Technology Brookhaven National Laboratory Associated Universities, Inc. Upton, Long Island, New York 11973 Under Contract No. DE-AC02-76CH00016 with the M A QTED United States Department of Energy *»! fl U I L P DISTRIBUTION OF THIS DOCUMENT IS UNLIMITED DISCLAIMER This report was prepared as an account of work sponsored by an agency of the United States Government. Neither the United States Government nor any agency thereof, nor any of their employees, not any of their contractors, subcontractors, or their employees, makes any warranty, express or implied, or assumes any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency, contractor, or subcontractor thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency, contractor or subcontractor thereof. ii TABLE OF CONTENTS Page 1. Agenda 1 2. Summary of the U.S. Nuclear Reaction Data Network Meeting M.R. Bhat, BNL 3 3. Attachment 1 Description of the U.S.
    [Show full text]
  • Isotope Science Facility at Michigan State University: Nuclear Astrophysics
    3. Nuclear astrophysics Nuclear reactions in stars and stellar explosions generate energy and are respon- 3 sible for the ongoing synthesis of the elements. They are, therefore, at the heart of many astrophysical phenomena, such as stars, novae, supernovae, and X-ray bursts. Nuclear physics determines the signatures of isotopic and elemental abun- dances found in the spectra of these objects, in characteristic γ radiation from nu- clear decay, or in the composition of meteorites and presolar grains. The field of nuclear astrophysics ties together nuclear and particle physics on the microscopic scale with the physics of stars, galaxies, and the cosmos in a broad interdisciplin- ary approach. While some of the major open questions of the field have been asked for decades, many others are new, mostly posed by advances in astronomical ob- servations. An example is the discovery of r-process abundance patterns in stars through high-resolution spectroscopic observations with ground-based observa- tories (for example Keck and VLT) as well as the Hubble Space Telescope. More of these stars are being discovered through extensive surveys, such as the Ham- burg/ESO R-process Enhanced Star Survey (HERES) or the ongoing Sloan Exten- sion for Galactic Understanding and Exploration (SEGUE). Superbursts, absorp- tion lines, and ms-oscillations are new phenomena discovered in X-ray bursts by the Chandra X-ray observatory, XMM-Newton, the Rossi X-ray Timing Explorer (RXTE), and Beppo-SAX. Many, if not most of the current open questions of the field require understanding of the physics of unstable nuclei. Though pioneering advances have been made, progress has been hampered by limited beam intensi- ties at current rare isotope beam facilities.
    [Show full text]
  • Uncertainties in Radiative Neutron-Capture Rates Relevant to the a ∼ 80 R-Process Peak
    Uncertainties in radiative neutron-capture rates relevant to the A ∼ 80 r-process peak I. K. B. Kullmann,1, ∗ E. W. Hafli,1 A. C. Larsen,1,† and E. Lima1 1Department of Physics, University of Oslo, N-0316 Oslo, Norway (Dated: January 24, 2018) The rapid neutron-capture process (r-process) has for the first time been confirmed to take place in a neutron- star merger event. A detailed understanding of the rapid neutron-capture process is one of the holy grails in nuclear astrophysics. In this work we investigate one aspect of the r-process modelling: uncertainties in radiative neutron-capture cross sections and astrophysical reaction rates for isotopes of the elements Fe, Co, Ni, Cu, Zn, Ga, Ge, As, and Se. In particular, we study deviations from standard libraries used for astrophysics, and the influence of a very-low g-energy enhancement in the average, reduced g-decay probability on the (n;g) rates. We find that the intrinsic uncertainties are in some cases extremely large, and that the low-energy enhancement, if present in neutron-rich nuclei, may increase the neutron-capture reaction rate significantly. I. INTRODUCTION as the r-process was observed live for the first time. the Ad- vanced LIGO and Advanced Virgo gravitational-wave detec- One of the ”Eleven Science Questions for the New Cen- tors made the first discovery of a neutron-star binary merger tury” [1] concerns the formation of elements from iron to named GW170817 [12]. The gravitational-wave observation uranium in stellar environments. Although the main pro- was immediately followed up by measuring the electromag- cesses responsible for the heavy-element creation were out- netic radiation of GW170817 over a broad range of frequen- lined already in 1957 by Burbidge et al.
    [Show full text]