DOCSLIB.ORG

Geometry of Families of Curves Described by Conchoids

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Geometry of Families of Curves Described by Conchoids The Geometry of Some Families of Curves Described by Conchoids A conchoid is a way of deriving a new curve based on a given curve, a fixed point, and a positive constant k. Curves generated in this way are sometimes called general conchoids because this method is a generalization of the conchoid of Nicomedes. Step-by-step construction: 1. Specify a curve C, a point O not on C , and a constant k. 2. Draw a line l passing thru O and any point P on C. 3. Mark points Q1 and Q2 on l such that distance[Q1,P] = distance[Q2,P] = k. 4. The locus of Q1 and Q2 for all variable points P on C is the conchoid of C with respect to O and offset k. The point O is called the pole. In general, if the equation of the given curve is r = f ( θ ) in polar coordinates, then the equation of its conchoid has the form: r = f ( θ ) ± k. Examples 1. The conchoid of a sinusoid with pole at ( 3, – 3 ) and offset k = 2 is displayed in the figure below. This conchoid is the pair of continuous curves formed as the union of all the bold dots in the plane. O = ( 3, – 3 ) 2. The Conchoid of Nicomedes, as shown in the figure, refers to an entire family of curves of one parameter. Each branch curve in the family is the conchoid of a common horizontal line (which is asymptotic to the curve). 1 If the asymptote to the Conchoid of Nicomedes is the line with the polar equation: r = a csc ( θ ) then the polar equation for each member curve is: r = a csc ( θ ) ± k for some number k. Step-by-step construction: m 1. Specify a line , a point O not on l, and an l offset distance k. Q1 2. Draw a line m passing through O and any point P on l. 3. Mark points Q1 and Q2 on m such that l distance[Q1,P] = distance[Q2,P] = k. 4. The locus of Q1 and Q2 for variable points P on l is a member of the Q2 Conchoid of Nicomedes. 3. The Limacon of Pascal refers to another family of curves of one parameter. Each member of this family is describable as the conchoid of a common circle. Limacon of Pascal and an artistic reflection Step-by-step construction: 1. Specify a fixed point O on a circle. 2. Draw a line l passing through O and P, where P is any point on the circle. 3. On line l, mark points Q1 and Q2 such that distance [P, Q1] = distance[P, Q2] = k, O O where k is the offset constant. 4. Repeat steps 2, 3 for all possible choices of P. 5. The locus of Q1 and Q2 is the Limacon of Pascal. 2 The graph of a curve included in the Limacon of Pascal may have one of four distinct shapes based upon the relative magnitudes of the radii of the fixed circle and that of the offset constant k which are described in the step-by-step construction procedure. Case 1. Consider the graph of the conchoid of the circle: r = 2 sin θ with offset value k = 1. It is called an inner loop limacon. This curve has the polar equation: r = 1 + 2 sin θ and is displayed below. In general, the polar graph of the equation r = a + b sin θ is an inner loop limacon a whenever < 1. b 3 Case 2. The graph of the conchoid of the circle: r = 2 sin θ with offset value, k = 2, is called a cardioid. It has the polar equation: r = 2 + 2 sin θ and is displayed below. In general, the polar graph of the equation r = a + a sin θ is called a cardioid. 4 Case 3. The graph of the conchoid of the circle: r = 2 sin θ with offset value, k = 11 , is called a 4 dimpled limacon. It has polar equation: r = 11 + 2 sin θ and is shown below. 4 In general, the polar graph of the equation r = a + b sin θ is a dimpled limacon a whenever 1 < < 2. b 5 Case 4. The graph of the conchoid of the circle: r = 2 sin θ with offset value, k = 4, is called a convex limacon. It has the polar equation: r = 4 + 2 sin θ and the graph shown below. In general, the polar graph of the equation r = a + b sin θ is a convex limacon a whenever > 2. b 6 Details on Nicomedes Conchoid A plane algebraic curve of order 4 whose equation in Cartesian rectangular coordinates has the form (x 2 + y 2 )(y − a) 2 − k 2 y 2 = 0 and in polar coordinates r = a cscθ ± k. The outer (upper) branch has asymptote: y = a and two points of inflection. The inner (lower) branch has asymptote y = a . The character of the coordinate origin depends on the values of k and a. For a < k it is a node, i.e. a double point of self-intersection; For a = k it is a cusp; the curve has the y-axis as a common semi-tangent line from both sides at the origin. For a > k it is an isolated point and, in addition, the curve has two symmetric points of inflection with respect to the y axis. The curve is a conchoid of the straight line y = a. It is named after Nicomedes (3rd century B.C.), who used it to solve the problem of trisecting an angle. 7 Angle Trisection________________________________________________________ The conchoid can be used to solve the Greek Angle Trisection problem. 1 rd Given an acute angle ;AOB, we want to construct an angle that is the measure of 3 ;AOB, with the help of a conchoid of Nicomedes. Steps: 1. Draw a line m intersecting segment AO and perpendicular to it. 2. Mark the points: D = m ∩ AO and L = m ∩ BO . 3. Construct a conchoid of Nicomedes of the line m with pole at O and offset k = 2 × distance[O,L]. 4. Draw line l intersecting L and perpendicular to m. 5. Let C be an intersection of the curve and l, the one on the opposite side of the pole. Then measure(;AOB )= 3× measure(;AOC ). Nichomedes constructed his conchoid for angle trisection by means of a mechanical device, thus: AB is a ruler with a slot in it parallel to its length, FE a second ruler fixed at right angles to the first with a peg (C) fixed in it. A third ruler, PC, pointed at P, has a slot in it, parallel to its length, which fits the peg C. D is a fixed peg on PC in a straight line with the slot but on the under-side, and this peg D moves freely along the slot in AB. If then the ruler PC moves so that the peg D describes the length of the slot in AB on each side of F, the extremity P of the ruler describes the curve which is called a conchoid. Nichomedes called the straight line AB the ruler, the fixed point C the pole, and the constant length PD the distance. 8.
Load more

Recommended publications
  • Some Curves and the Lengths of Their Arcs Amelia Carolina Sparavigna
    Some Curves and the Lengths of their Arcs Amelia Carolina Sparavigna To cite this version: Amelia Carolina Sparavigna. Some Curves and the Lengths of their Arcs. 2021. hal-03236909 HAL Id: hal-03236909 https://hal.archives-ouvertes.fr/hal-03236909 Preprint submitted on 26 May 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Some Curves and the Lengths of their Arcs Amelia Carolina Sparavigna Department of Applied Science and Technology Politecnico di Torino Here we consider some problems from the Finkel's solution book, concerning the length of curves. The curves are Cissoid of Diocles, Conchoid of Nicomedes, Lemniscate of Bernoulli, Versiera of Agnesi, Limaçon, Quadratrix, Spiral of Archimedes, Reciprocal or Hyperbolic spiral, the Lituus, Logarithmic spiral, Curve of Pursuit, a curve on the cone and the Loxodrome. The Versiera will be discussed in detail and the link of its name to the Versine function. Torino, 2 May 2021, DOI: 10.5281/zenodo.4732881 Here we consider some of the problems propose in the Finkel's solution book, having the full title: A mathematical solution book containing systematic solutions of many of the most difficult problems, Taken from the Leading Authors on Arithmetic and Algebra, Many Problems and Solutions from Geometry, Trigonometry and Calculus, Many Problems and Solutions from the Leading Mathematical Journals of the United States, and Many Original Problems and Solutions.
    [Show full text]
  • The Math in “Laser Light Math”
    The Math in “Laser Light Math” When graphed, many mathematical curves are beautiful to view. These curves are usually brought into graphic form by incorporating such devices as a plotter, printer, video screen, or mechanical spirograph tool. While these techniques work, and can produce interesting images, the images are normally small and not animated. To create large-scale animated images, such as those encountered in the entertainment industry, light shows, or art installations, one must call upon some unusual graphing strategies. It was this desire to create large and animated images of certain mathematical curves that led to our design and implementation of the Laser Light Math projection system. In our interdisciplinary efforts to create a new way to graph certain mathematical curves with laser light, Professor Lessley designed the hardware and software and Professor Beale constructed a simplified set of harmonic equations. Of special interest was the issue of graphing a family of mathematical curves in the roulette or spirograph domain with laser light. Consistent with the techniques of making roulette patterns, images created by the Laser Light Math system are constructed by mixing sine and cosine functions together at various frequencies, shapes, and amplitudes. Images created in this fashion find birth in the mathematical process of making “roulette” or “spirograph” curves. From your childhood, you might recall working with a spirograph toy to which you placed one geared wheel within the circumference of another larger geared wheel. After inserting your pen, then rotating the smaller gear around or within the circumference of the larger gear, a graphed representation emerged of a certain mathematical curve in the roulette family (such as the epitrochoid, hypotrochoid, epicycloid, hypocycloid, or perhaps the beautiful rose family).
    [Show full text]
  • Polar Graphs
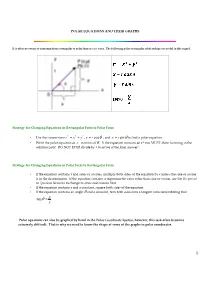
    POLAR EQUATIONS AND THEIR GRAPHS It is often necessary to transform from rectangular to polar form or vice versa. The following polar-rectangular relationships are useful in this regard. Strategy for Changing Equations in Rectangular Form to Polar Form 2 2 2 • Use the conversions r= x + y , x= r cos θ , and x= r sin θ to find a polar equation. • Write the polar equation as r in terms of θ . If the equation contains an r 2 you MUST show factoring in the solution path! DO NOT EVER divide by r to arrive at the final answer! Strategy for Changing Equations in Polar Form to Rectangular Form • If the equation contains r and sines or cosines, multiply both sides of the equation by r unless the sine or cosine is in the denominator. If the equation contains a trigonometric ratio other than sine or cosine, use the Reciprocal or Quotient Identities to change to sines and cosines first. • If the equation contains r and a constant, square both sides of the equation. • If the equation contains an angle θ and a constant, turn both sides into a tangent ratio remembering that y tan θ = . x Polar equations can also be graphed by hand in the Polar Coordinate System , however, this task often becomes extremely difficult. That is why we need to know the shape of some of the graphs in polar coordinates. 1 For the following "special" polar equations you need to be able to associate their name with their characteristics and graphs! Equations of Circles Circles with center along one of the coordinate axes and radius a Circle with center at the origin and radius a.
    [Show full text]
  • An Algebraic Analysis of Conchoids to Algebraic Curves
    An algebraic analysis of conchoids to algebraic curves J. R. Sendra • J. Sendra Abstract We study the conchoid to an algebraic affine plane curve C from the perspective of algebraic geometry, analyzing their main algebraic properties. Beside C, the notion of conchoid involves a point A in the affine plane (the focus) and a non­ zero field element d (the distance). We introduce the formal definition of conchoid by means of incidence diagrams. We prove that the conchoid is a 1-dimensional algebraic set having at most two irreducible components. Moreover, with the exception of circles centered at the focus A and taking d as its radius, all components of the corresponding conchoid have dimension 1. In addition, we introduce the notions of special and sim­ ple components of a conchoid. Furthermore we state that, with the exception of lines passing through A, the conchoid always has at least one simple component and that, for almost every distance, all the components of the conchoid are simple. We state that, in the reducible case, simple conchoid components are birationally equivalent to C, and we show how special components can be used to decide whether a given algebraic curve is the conchoid of another curve. 1 Introduction The notion of conchoid is classical and is derived from a fixed point, a plane curve, and a length in the following way. Let C be a plane curve (the base curve), A a fixed point Focus A Fig. 1 Left conchoid geometric construction. Right conchoid of a circle with focus on it in the plane (the focus), and d a non-zero fixed field element (the distance).
    [Show full text]
  • Slant Helices Generated by Plane Curves in Euclidean 3-Space Mesut Altınok and Levent Kula
    Palestine Journal of Mathematics Vol. 5(2) (2016) , 164–174 © Palestine Polytechnic University-PPU 2016 Slant Helices Generated by Plane Curves in Euclidean 3-space Mesut Altınok and Levent Kula Communicated by Ayman Badawi MSC 2010 Classifications: Primary 53A04 ; Secondary 14H50. Keywords and phrases: Slant helix, plane curve and principal normal indicatrix. Abstract In this paper, we investigate the relationship between the plane curves and slant helices in R3. Moreover, we show how could be obtained to a slant helix from a plane curve. Finally, we give some slant helix examples generated by plane curves in Euclidean 3-space. 1 Introduction In [3], A slant helix in Euclidean space R3 was defined by the property that the principal normal makes a constant angle with a fixed direction. Moreover, Izumiya and Takeuchi showed that γ is a slant helix in R3 if and only if the geodesic curvature of the principal normal of a space curve γ is a constant function. In [5], Kula and Yayli have studied spherical images of tangent indicatrix and binormal indi- catrix of a slant helix and they showed that the spherical images are spherical helix. In [4], Kula, Ekmekci, Yayli and Ilarslan have studied the relationship between the plane curves and slant helices in R3. They obtained that the differential equations which are character- izations of a slant helix. In this paper we consider the relationship between the plane curves and slant helices in R3. Moreover, we get slant helix from plane curve. Also, we give some slant helix examples in Euclidean 3-space. 2 Preliminaries We now recall some basic concept on classical geometry of space curves and the definition of slant helix in R3.
    [Show full text]
  • Collected Atos
    Mathematical Documentation of the objects realized in the visualization program 3D-XplorMath Select the Table Of Contents (TOC) of the desired kind of objects: Table Of Contents of Planar Curves Table Of Contents of Space Curves Surface Organisation Go To Platonics Table of Contents of Conformal Maps Table Of Contents of Fractals ODEs Table Of Contents of Lattice Models Table Of Contents of Soliton Traveling Waves Shepard Tones Homepage of 3D-XPlorMath (3DXM): http://3d-xplormath.org/ Tutorial movies for using 3DXM: http://3d-xplormath.org/Movies/index.html Version November 29, 2020 The Surfaces Are Organized According To their Construction Surfaces may appear under several headings: The Catenoid is an explicitly parametrized, minimal sur- face of revolution. Go To Page 1 Curvature Properties of Surfaces Surfaces of Revolution The Unduloid, a Surface of Constant Mean Curvature Sphere, with Stereographic and Archimedes' Projections TOC of Explicitly Parametrized and Implicit Surfaces Menu of Nonorientable Surfaces in previous collection Menu of Implicit Surfaces in previous collection TOC of Spherical Surfaces (K = 1) TOC of Pseudospherical Surfaces (K = −1) TOC of Minimal Surfaces (H = 0) Ward Solitons Anand-Ward Solitons Voxel Clouds of Electron Densities of Hydrogen Go To Page 1 Planar Curves Go To Page 1 (Click the Names) Circle Ellipse Parabola Hyperbola Conic Sections Kepler Orbits, explaining 1=r-Potential Nephroid of Freeth Sine Curve Pendulum ODE Function Lissajous Plane Curve Catenary Convex Curves from Support Function Tractrix
    [Show full text]
  • Projecting Mathematical Curves with Laser Light
    Bridges 2011: Mathematics, Music, Art, Architecture, Culture Projecting Mathematical Curves with Laser Light Merrill Lessley* Department of Theatre and Dance • University of Colorado Boulder [email protected] Paul Beale Department of Physics • University of Colorado Boulder Abstract This paper describes the math and technology required to project a variety of mathematical curves with an innovative laser light control system. The focus is upon creating large-scale animated laser projections of spirograph shapes, such as those found among the epitrochoid, hypotrochoid, epicycloid, and hypocycloid curves. The process described utilizes an unusual math approach that was first presented by the Greek or Egyptian mathematician/astronomer Ptolemy. Instead of using the traditional spirograph techniques of rotating one wheel outside or inside of another wheel, the Laser Light Math system is structured around Ptolemy’s idea of epicycles where one circle's center moves on the circumference of another circle. Traditional equations are modified to consider fully the elements of frequency, rotational direction, diameter, and offset. Introduction When graphed, many mathematical curves are beautiful to view. These curves are often brought into graphic form by incorporating such devices as a plotter, printer, video screen, or mechanical spirograph tool. While these techniques work, and can produce interesting results, the images are normally small and not animated. To create large-scale animated images, such as those encountered in the entertainment industry, light shows, or art installations, one must use some unusual graphing strategies. This desire to create large and animated images of certain mathematical curves led to our design and implementation of the Laser Light Math projection system.
    [Show full text]
  • The Mathematical Gazette Index for 1894 to 1908
    The Mathematical Gazette Index for 1894 to 1908 AUTHOR TITLE PAGE Issue Category C.W.Adams Stability of cube floating in liquid p. 388 Dec 1908 MNote 285 V.Ramaswami Aiyar Extension of Euclid I.47 to n-sided regular polygons p. 109 June 1897 MNote 41 V.Ramaswami Aiyar On a fundamental theorem in inversion p. 88 Oct 1904 MNote 153 V.Ramaswami Aiyar On a fundamental theorem in inversion p. 275 Jan 1906 MNote 183 V.Ramaswami Aiyar Note on a point in the demonstration of the binomial theorem p. 276 Jan 1906 MNote 185 V.Ramaswami Aiyar Note on the power inequality p. 321 May 1906 MNote 192 V.Ramaswami Aiyar On the exponential inequalities and the exponential function p. 8 Jan 1907 Article V.Ramaswami Aiyar The A, B, C of the higher analysis p. 79 May 1907 Article V.Ramaswami Aiyar On Stolz and Gmeiner’s proof of the sine and cosine series p. 282 June 1908 MNote 259 V.Ramaswami Aiyar A geometrical proof of Feuerbach’s theorem p. 310 July 1908 MNote 264 A.O.Allen On the adjustment of Kater’s pendulum p. 307 May 1906 Article A.O.Allen Notes on the theory of the reversible pendulum p. 394 Dec 1906 Article Anonymous Proof of a well-known theorem in geometry p. 64 Oct 1896 MNote 30 Anonymous Notes connected with the analytical geometry of the straight line p. 158 Feb 1898 MNote 49 Anonymous Method of reducing central conics p. 225 Dec 1902 MNote 110B (note) Anonymous On a fundamental theorem in inversion p.
    [Show full text]
  • Seashell Interpretation in Architectural Forms
    Seashell Interpretation in Architectural Forms From the study of seashell geometry, the mathematical process on shell modeling is extremely useful. With a few parameters, families of coiled shells were created with endless variations. This unique process originally created to aid the study of possible shell forms in zoology. The similar process can be developed to utilize the benefit of creating variation of the possible forms in architectural design process. The mathematical model for generating architectural forms developed from the mathematical model of gastropods shell, however, exists in different environment. Normally human architectures are built on ground some are partly underground subjected different load conditions such as gravity load, wind load and snow load. In human architectures, logarithmic spiral is not necessary become significant to their shapes as it is in seashells. Since architecture not grows as appear in shells, any mathematical curve can be used to replace this, so call, growth spiral that occur in the shells during the process of growth. The generating curve in the shell mathematical model can be replaced with different mathematical closed curve. The rate of increase in the generating curve needs not only to be increase. It can be increase, decrease, combination between the two, and constant by ignore this parameter. The freedom, when dealing with architectural models, has opened up much architectural solution. In opposite, the translation along the axis in shell model is greatly limited in architecture, since it involves the problem of gravity load and support condition. Mathematical Curves To investigate the possible architectural forms base on the idea of shell mathematical models, the mathematical curves are reviewed.
    [Show full text]
  • Design and Implementation of Conchoid and Offset Processing Maple Packages
    The final journal version of this paper appears in Juana Sendra, David Gómez, Valerio Morán, "Design and Implementation of Maple Packages for Processing Offsets and Conchoids" Annals of Mathematics and Artificial Intelligence (2016). DOI: 10.1007/s10472-016-9504-z and it is available at link.springer.com Design and Implementation of Conchoid and O®set Processing Maple Packages Juana Sendra1, David G¶omez2 and Valerio Mor¶an2 1 Dpto. de Matem¶aticaAplicada a la I.T. de Telecomunicaci¶on. Research Center on Software Technologies and Multimedia Systems for Sustainability (CITSEM) Universidad Polit¶ecnicade Madrid (UPM) 2 E.U.I.T.Telecomunicaci¶on, Universidad Polit¶ecnicade Madrid E-28031 Madrid, Spain Abstract. This paper is framed within the problem of analyzing the rationality of the components of two classical geometric constructions, namely the o®set and the conchoid to an algebraic plane curve and, in the a±rmative case, the actual computation of parametrizations. We recall some of the basic de¯nitions and main properties on o®sets (see [18]), and conchoids (see [20]) as well as the algorithms for parametrizing their rational components (see [1] and [21], respectively). Moreover, we implement the basic ideas creating two package in the computer algebra system Maple to analyze the rationality of conchoids and o®set curves, as well as the corresponding help pages. In addition, we present a brief atlas where the o®set and conchoids of several algebraic plane curves are obtained, its rationality analyzed, and parametrizations are provided using the created packages. Key Words: O®set Curves, Conchoids Curves, Rational curves, parametrization, symbolic mathe- matical software, computer-aided geometric design.
    [Show full text]
  • The Trisection Problem. INSTITUTION National Council of Teachers of Mathematics, Inc., Washington, D.C
    DOCUMENT RESUME ED 058 058 SE 013 133 AUTHOR Yates, Robert C. TITLE The Trisection Problem. INSTITUTION National Council of Teachers of Mathematics, Inc., Washington, D.C. PUB DATE 71 NOTE 78p. EDRS PRICE ME-S0.65 BC-$3.29 DESCRIPTORS *Algebra; Geometry; *Mathematical Enrichment; Mathematics; Mathematics Education; *Plane Geometry; Science History; *Secondary School Mathematics; *Trigonometry IDENTIFIERS Mathematics History ABSTRACT This book, photographically reproduced from its original 1942 edition, is an extended essay on one of the three problems of the ancients. The first chanter reduces the problem of trisecting an angle to the solution of a cubic equation, shows that straightedge and compasses constructions can only give lengths of a certain form, and then proves that many angles give an equation which does not have anv roots of this form. The secoad chapter explains how various cu7ves (including the hyperbola and the parabola) can be used to trisecl: any angle, and the third chapter describes several mechanical devices for doing the same thing. Approximate methods are discussed and compared in the fourth chapter, and the final chapter is devoted to some fallacious solutions. The whole book has an interesting historical flavor. The mathematics used rarely goes beyond secondary school algebra and trigonometry. (MM) U.S. DEPARTMENT CIP HEALTH, EDUCATION 8, WELFARE OFFICE OF EDUCATION THIS DOCUMENT HAS PEEN REPRO, DUCED EXACTLY AS RECEIVED FROM THE PERSON OR ORGANIZATION ORM- INATING IT. POINTS OE VIEW OR OPIN- IONS STATED DO NOT NECESSARILY REPRESENI OFFICIAL OFFICE OF EDU- CATION POSITION OR POLICY. Classics in Mathomati4s Education A Series THE TRISECTION PROBLEM CLASSI C S IN MATHEMATICS EDUCATION Volume I:The Pythagorean Proposition Elisha Scott Loomis Volume 2: Number Stories of Long Ago by David Eugene Smith Volume 3:The Trisection Problem by Robert C.
    [Show full text]
  • Classification of Cyclic Surfaces and Geometrical Research of Canal Surfaces
    IJRRAS 12 (3) ● September 2012 www.arpapress.com/Volumes/Vol12Issue3/IJRRAS_12_3_03.pdf CLASSIFICATION OF CYCLIC SURFACES AND GEOMETRICAL RESEARCH OF CANAL SURFACES S.N. Krivoshapko1 & Christian A. Bock Hyeng2 1Peoples’ Friendship University of Russia, 6 Miklukho-Maklaya Str. Moscow, 117198, Russia 2North Carolina Agricultural and Technical State University, 1601 E. Market St. Greensboro, NC 27411 USA, Phone: 336-334-7199 Email: [email protected] ABSTRACT This review article is devoted to an analysis of the literature on the geometric researches of cyclic surfaces with generating circles of constant and various diameters. The shells with cyclic middle surfaces are particularly useful as connecting parts of pipelines, in spiral chambers of turbines in hydroelectric power stations, in public and commercial buildings, for example, as coverings of stadiums, in water attractions, and so on. This review article contains 45 references, and these are practically all original sources dealing with geometry of canal surfaces and with classification of cyclic surfaces. Keywords: Cyclic surfaces, Canal surfaces, Differential geometry, Computer graphics, Classification of surfaces, Geometrical computer aided design. 1. INTRODUCTION The investigation of the class of cyclic surfaces started from the research of tubular surfaces of constant diameter having straight or curvilinear axes. Further, many subclasses and types of cyclic surfaces were discovered and examined. Some cyclic surfaces have been named in honor of the geometricians presented these surfaces for the applications. For example, one may mention Joachimsthal’s surface, Dupin’s cyclides, or the surface of Virich. It should be noted that surfaces of revolution are the cyclic surfaces with straight axis but they are singled out into a special class of Surfaces of Revolution, which is why these surfaces will not be presented in this review.
    [Show full text]