Kepler's Ellipse Generated by the Trigonometrically Organized Gravitons
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Mathematicians
MATHEMATICIANS [MATHEMATICIANS] Authors: Oliver Knill: 2000 Literature: Started from a list of names with birthdates grabbed from mactutor in 2000. Abbe [Abbe] Abbe Ernst (1840-1909) Abel [Abel] Abel Niels Henrik (1802-1829) Norwegian mathematician. Significant contributions to algebra and anal- ysis, in particular the study of groups and series. Famous for proving the insolubility of the quintic equation at the age of 19. AbrahamMax [AbrahamMax] Abraham Max (1875-1922) Ackermann [Ackermann] Ackermann Wilhelm (1896-1962) AdamsFrank [AdamsFrank] Adams J Frank (1930-1989) Adams [Adams] Adams John Couch (1819-1892) Adelard [Adelard] Adelard of Bath (1075-1160) Adler [Adler] Adler August (1863-1923) Adrain [Adrain] Adrain Robert (1775-1843) Aepinus [Aepinus] Aepinus Franz (1724-1802) Agnesi [Agnesi] Agnesi Maria (1718-1799) Ahlfors [Ahlfors] Ahlfors Lars (1907-1996) Finnish mathematician working in complex analysis, was also professor at Harvard from 1946, retiring in 1977. Ahlfors won both the Fields medal in 1936 and the Wolf prize in 1981. Ahmes [Ahmes] Ahmes (1680BC-1620BC) Aida [Aida] Aida Yasuaki (1747-1817) Aiken [Aiken] Aiken Howard (1900-1973) Airy [Airy] Airy George (1801-1892) Aitken [Aitken] Aitken Alec (1895-1967) Ajima [Ajima] Ajima Naonobu (1732-1798) Akhiezer [Akhiezer] Akhiezer Naum Ilich (1901-1980) Albanese [Albanese] Albanese Giacomo (1890-1948) Albert [Albert] Albert of Saxony (1316-1390) AlbertAbraham [AlbertAbraham] Albert A Adrian (1905-1972) Alberti [Alberti] Alberti Leone (1404-1472) Albertus [Albertus] Albertus Magnus -

Plato As "Architectof Science"
Plato as "Architectof Science" LEONID ZHMUD ABSTRACT The figureof the cordialhost of the Academy,who invitedthe mostgifted math- ematiciansand cultivatedpure research, whose keen intellectwas able if not to solve the particularproblem then at least to show the methodfor its solution: this figureis quite familiarto studentsof Greekscience. But was the Academy as such a centerof scientificresearch, and did Plato really set for mathemati- cians and astronomersthe problemsthey shouldstudy and methodsthey should use? Oursources tell aboutPlato's friendship or at leastacquaintance with many brilliantmathematicians of his day (Theodorus,Archytas, Theaetetus), but they were neverhis pupils,rather vice versa- he learnedmuch from them and actively used this knowledgein developinghis philosophy.There is no reliableevidence that Eudoxus,Menaechmus, Dinostratus, Theudius, and others, whom many scholarsunite into the groupof so-called"Academic mathematicians," ever were his pupilsor close associates.Our analysis of therelevant passages (Eratosthenes' Platonicus, Sosigenes ap. Simplicius, Proclus' Catalogue of geometers, and Philodemus'History of the Academy,etc.) shows thatthe very tendencyof por- trayingPlato as the architectof sciencegoes back to the earlyAcademy and is bornout of interpretationsof his dialogues. I Plato's relationship to the exact sciences used to be one of the traditional problems in the history of ancient Greek science and philosophy.' From the nineteenth century on it was examined in various aspects, the most significant of which were the historical, philosophical and methodological. In the last century and at the beginning of this century attention was paid peredominantly, although not exclusively, to the first of these aspects, especially to the questions how great Plato's contribution to specific math- ematical research really was, and how reliable our sources are in ascrib- ing to him particular scientific discoveries. -

The Geodetic Sciences in Byzantium
The geodetic sciences in Byzantium Dimitrios A. Rossikopoulos Department of Geodesy and Surveying, Aristotle University of Thessaloniki [email protected] Abstract: Many historians of science consider that geodeasia, a term used by Aristotle meaning "surveying", was not particularly flourishing in Byzantium. However, like “lo- gistiki” (practical arithmetic), it has never ceased to be taught, not only at public universi- ties and ecclesiastical schools, as well as by private tutors. Besides that these two fields had to do with problems of daily life, Byzantines considered them necessary prerequisite for someone who wished to study philosophy. So, they did not only confine themselves to copying and saving the ancient texts, but they also wrote new ones, where they were ana- lyzing their empirical discoveries and their technological achievements. This is the subject of this paper, a retrospect of the numerous manuscripts of the Byzantine period that refer to the development of geodesy both in teaching and practices of surveying, as well as to mat- ters relating to the views about the shape of the earth, the cartography, the positioning in travels and generally the sciences of mapping. Keywords: Geodesy, geodesy in Byzantium, history of geodesy, history of surveying, history of mathematics. Περίληψη: Πολλοί ιστορικοί των επιστημών θεωρούν ότι η γεωδαισία, όρος που χρησι- μοποίησε ο Αριστοτέλης για να ορίσει την πρακτική γεωμετρία, την τοπογραφία, δεν είχε ιδιαίτερη άνθιση στο Βυζάντιο. Ωστόσο, όπως και η “λογιστική”, δεν έπαψε ποτέ να διδά- σκεται όχι μόνο στα κοσμικά πανεπιστήμια, αλλά και στις εκκλησιαστικές σχολές, καθώς επίσης και από ιδιώτες δασκάλους. Πέρα από το ότι οι δύο αυτοί κλάδοι είχαν να κάνουν με προβλήματα της καθημερινής ζωής των ανθρώπων, οι βυζαντινοί θεωρούσαν την διδα- σκαλία τους απαραίτητη προϋπόθεση ώστε να μπορεί κανείς να παρακολουθήσει μαθήμα- τα φιλοσοφίας. -

Apollonius of Pergaconics. Books One - Seven
APOLLONIUS OF PERGACONICS. BOOKS ONE - SEVEN INTRODUCTION A. Apollonius at Perga Apollonius was born at Perga (Περγα) on the Southern coast of Asia Mi- nor, near the modern Turkish city of Bursa. Little is known about his life before he arrived in Alexandria, where he studied. Certain information about Apollonius’ life in Asia Minor can be obtained from his preface to Book 2 of Conics. The name “Apollonius”(Apollonius) means “devoted to Apollo”, similarly to “Artemius” or “Demetrius” meaning “devoted to Artemis or Demeter”. In the mentioned preface Apollonius writes to Eudemus of Pergamum that he sends him one of the books of Conics via his son also named Apollonius. The coincidence shows that this name was traditional in the family, and in all prob- ability Apollonius’ ancestors were priests of Apollo. Asia Minor during many centuries was for Indo-European tribes a bridge to Europe from their pre-fatherland south of the Caspian Sea. The Indo-European nation living in Asia Minor in 2nd and the beginning of the 1st millennia B.C. was usually called Hittites. Hittites are mentioned in the Bible and in Egyptian papyri. A military leader serving under the Biblical king David was the Hittite Uriah. His wife Bath- sheba, after his death, became the wife of king David and the mother of king Solomon. Hittites had a cuneiform writing analogous to the Babylonian one and hi- eroglyphs analogous to Egyptian ones. The Czech historian Bedrich Hrozny (1879-1952) who has deciphered Hittite cuneiform writing had established that the Hittite language belonged to the Western group of Indo-European languages [Hro]. -
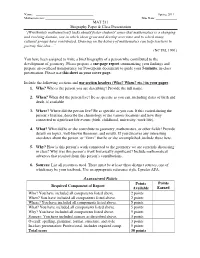
MAT 211 Biography Paper & Class Presentation
Name: Spring 2011 Mathematician: Due Date: MAT 211 Biography Paper & Class Presentation “[Worthwhile mathematical] tasks should foster students' sense that mathematics is a changing and evolving domain, one in which ideas grow and develop over time and to which many cultural groups have contributed. Drawing on the history of mathematics can help teachers to portray this idea…” (NCTM, 1991) You have been assigned to write a brief biography of a person who contributed to the development of geometry. Please prepare a one-page report summarizing your findings and prepare an overhead transparency (or Powerpoint document) to guide your 5-minute, in-class presentation. Please use this sheet as your cover page. Include the following sections and use section headers (Who? When? etc.) in your paper. 1. Who? Who is the person you are describing? Provide the full name. 2. When? When did the person live? Be as specific as you can, including dates of birth and death, if available. 3. Where? Where did the person live? Be as specific as you can. If this varied during the person’s lifetime, describe the chronology of the various locations and how they connected to significant life events (birth, childhood, university, work life). 4. What? What did he or she contribute to geometry, mathematics, or other fields? Provide details on topics, well-known theorems, and results. If you discover any interesting anecdotes about the person, or “firsts” that he or she accomplished, include those here. 5. Why? How is this person’s work connected to the geometry we are currently discussing in class? Why was this person’s work historically significant? Include mathematical advances that resulted from this person’s contributions. -

Bibliography
Bibliography Afshar, Iraj: Bibliographie des Catalogues des Manuscrits Persans. Tehran: 1958. Almagest: see Ptolemy. Apollonius: Apollonii Pergaei quae Graece exstant cum commentariis Eutocii (ed. J. L. Heiberg), 2 vols. Leipzig: 1891, 1893. Arberry, A. J. : The Chester Beatty Library, A Handlist of the Arabic Manuscripts, Vol. VII. Dublin: 1964. Archimedes: Archimedis Opera Omnia cum commentariis Eutocii, (iterum ed. J. L. Heiberg), 3 vols. Leipzig: 1910-1915. Archimedes: see also Heath. Aristarchus of Samos: On the Sizes and Distances of the Sun and Moon (ed. T. Heath). Oxford: 1913. Aristotle, Nicomachean Ethics: Aristotelis Ethica Nicomachea (ed. I. Bywater). Oxford: 1894. Aristotle, Prior Analytics: Aristotelis Analytica Priora et Posteriora (ed. W. D. Ross and L. Minio-Paluello). Oxford: 1964. Autolycus: J. Mogenet, Autolycus de Pitane. Louvain, 1950 (Universite de Louvain, Recueil de Travaux d'Histoire et de Philologie, 3e. Serie Fasc. 37). Awad, Gurgis: "Arabic Manuscripts in American Libraries". Sumer 1, 237-277 (1951). (Arabic). Bachmann, Peter: Galens Abhandlung dariiber, dal3 der vorziigliche Arzt Philosoph sein mul3. Gottingen: 1965 (Ak. Wiss. Gottingen, Nachrichten Phil. -hist. Kl. 1965.1). Belger, C.: "Ein neues Fragmentum Mathematicum Bobiense". Hermes 16, 261-84 (1881). Boilot, D. J.: "L'oeuvre d'al-Beruni, essai bibliographique". Melanges de l'Institut Dominicain d'Etudes Orientales du Caire ~, 161-256 (1955). Bretschneider, C. A.: Die Geometrie und die Geometer vor Eukleides. Leipzig: 1870. 217 Bib Ziography Brockelmann, Carl: Geschichte der Arabischen Litteratur, zweite den Supplementbanden angepasste Aunage, 2 vols. Leiden: 1943, 1949 [GAL] [and] Supplementbande I-III. Leiden: 1937, 1938, 1942 [S]. Bulmer-Thomas, I.: "Conon of Samos". Dictionary of Scientific Biography III, (New York), 391 (1971). -

On Some Borrowed and Misunderstood Problems in Greek Catoptrics
On Some Borrowed and Misunderstood Problems in Greek Catoptrics by ALEXANDERJONES Optics was one of the first sciences to which ancient Greek mathe- maticians attempted to apply the apparatus of geometry. They were most successful in describing geometrically certain phenomena of per- spective (as in Euclid’s Optics and parts of Pappus’s Collection, Book 6),less so in catoljtrics, the study of mirrors.’ The problems typically encountered in the surviving writings on catoptrics fall into two classes: those dealing with the reflection of rays cast from a luminous source such as the sun upon minors of plane or curved surface, and those involving the projection of lines of sight from the eye by way of a minor to an object. The most basic problem of the first class, to make a burning mirror, is solved correctly in Diocles’s On Burning Mirrors (ca. 200 B.C.) with both spherical and parabolic mirrors; other prob- lems were investigated by Diocles, by Anthemius (ca. A.D. 620) in his On Paradoxical Devices, and doubtless by other authors in the cen- turies between.2 In general these problems were amenable to geo- metrical treatment in antiquity because Hellenistic geometers were equipped to study the tangent lines to a wide range of curves (or the tangent planes to analogous surfaces) and the behaviour of straight lines in a given direction or through a given point .and inflected at the curve or surface at equal angles to the tangent at the point of in- cidence. Problems of the other class, in which it was required to make an ar- rangement of mirrors or a mirror with a special curvature, such that a *Institute for the History and Philosophy of Science and Technology, Victoria College, Univer- sity of Toronto, Toronto, Canada MSS 1K7. -

A Short History of Greek Mathematics
Cambridge Library Co ll e C t i o n Books of enduring scholarly value Classics From the Renaissance to the nineteenth century, Latin and Greek were compulsory subjects in almost all European universities, and most early modern scholars published their research and conducted international correspondence in Latin. Latin had continued in use in Western Europe long after the fall of the Roman empire as the lingua franca of the educated classes and of law, diplomacy, religion and university teaching. The flight of Greek scholars to the West after the fall of Constantinople in 1453 gave impetus to the study of ancient Greek literature and the Greek New Testament. Eventually, just as nineteenth-century reforms of university curricula were beginning to erode this ascendancy, developments in textual criticism and linguistic analysis, and new ways of studying ancient societies, especially archaeology, led to renewed enthusiasm for the Classics. This collection offers works of criticism, interpretation and synthesis by the outstanding scholars of the nineteenth century. A Short History of Greek Mathematics James Gow’s Short History of Greek Mathematics (1884) provided the first full account of the subject available in English, and it today remains a clear and thorough guide to early arithmetic and geometry. Beginning with the origins of the numerical system and proceeding through the theorems of Pythagoras, Euclid, Archimedes and many others, the Short History offers in-depth analysis and useful translations of individual texts as well as a broad historical overview of the development of mathematics. Parts I and II concern Greek arithmetic, including the origin of alphabetic numerals and the nomenclature for operations; Part III constitutes a complete history of Greek geometry, from its earliest precursors in Egypt and Babylon through to the innovations of the Ionic, Sophistic, and Academic schools and their followers. -

Bibliography of the Publications of Abraham Wasserstein
Bibliography of the Publications of Abraham Wasserstein 1953 ‘The Manuscript Tradition of Statius’ Silvae’, Classical Quarterly, N.S. 3, pp. 69-78. 1955 ‘Thales’ Determination of the Diameters of the Sun and Moon’, Journal of Hellenic Studies, 75, pp. 114-16. 1956 ‘Thales and the Diameter of the Sun and Moon’, Journal of Hellenic Studies, 76, p. 105. ‘Politian’s Commentary on the Silvae of Statius’, Scriptorium, 10, pp. 83-9. review of ΜΊ. Finley, The World of Odysseus, Library Review, p. 451. contribution to ‘The position of language in philosophy, logic and social anthropology’, in Proceedings of the Seventh International Congress of Linguistics (London, 1952), pp. 243-45. 1957 review of J. Forsdyke, Greece Before Homer, Library Review, p. 7. 1958 ‘The Manuscript Tradition of Statius’ Silvae’, Classical Quarterly, N.S. 8, pp. 111- 12. ‘Theaetetus and the History of the Theory of Numbers’, Classical Quarterly, N.S. 8, pp. 165-79. review of V. Ehrenberg, Sophokles und Perikies, Gnomon, 30, pp. 169-74. review of C. Seltman, Riot in Ephesus, and of R. Graves, Greek Myths, Library Review, p. 353. review of Τ.ΒἜ. Webster, From Mycenae to Homer, Library Review, p. 503. 1959 ‘Some Early Greek Attempts to Square the Circle’, Phronesis, 4, pp. 92-100. review of Μ. Clagett, Greek Science in Antiquity, Journal of Hellenic Studies, 79, pp. 174-75. review of J. Chadwick, The Decipherment of Linear B, Library Review, p. 13. Scripta Classica Israelica vol. XV 1996 pp. 7-15 8 BIBLIOGRAPHY OF ABRAHAM WASSERSTEIN review of C.H. Whitoian, Homer and the Heroic Tradition, Library Review, p. -

What Does Euclid Have to Say About the Foundations Of
WHAT DOES EUCLID HAVE TO SAY ABOUT THE FOUNDATIONS OF COMPUTER SCIENCE? D. E. STEVENSON Abstract. It is fair to say that Euclid's Elements has b een a driving factor in the developmentof mathematics and mathematical logic for twenty-three centuries. The author's own love a air with mathematics and logic start with the Elements. But who was the man? Do we know anything ab out his life? What ab out his times? The contemp orary view of Euclid is much di erent than the man presented in older histories. And what would Euclid say ab out the status of computer science with its rules ab out everything? 1. Motivations Many older mathematicians mayhave started their love a air with mathematics with a high scho ol course in plane geometry. Until recently, plane geometry was taught from translations of the text suchasby Heath [5]. In myown case, it was the neat, clean picture presented with its neat, clean pro ofs. I would guess that over the twenty-three hundred year history of the text, Euclid must be the all-time, b est selling mathematics textb o ok author. At the turn of the last century, David Hilb ert also found a love of Euclid. So much so that Hilb ert was moved to prop ose his Formalist program for mathematics. Grossly over-simpli ed, Hilb ert prop osed that mathematics was a \meaningless game" in that the rules of logic preordained the results indep endent of any interpretation. Hilb ert was rather vehemently opp osed by L. E. -

Lecture 11. Apollonius and Conic Sections
Lecture 11. Apollonius and Conic Sections Figure 11.1 Apollonius of Perga Apollonius of Perga Apollonius (262 B.C.-190 B.C.) was born in the Greek city of Perga, close to the southeast coast of Asia Minor. He was a Greek geometer and astronomer. His major mathematical work on the theory of conic sections had a very great influence on the development of mathematics and his famous book Conics introduced the terms parabola, ellipse and hyperbola. Apollonius' theory of conics was so admired that it was he, rather than Euclid, who in antiquity earned the title the Great Geometer. He also made contribution to the study of the Moon. The Apollonius crater on the Moon was named in his honor. Apollonius came to Alexandria in his youth and learned mathematics from Euclid's successors. As far as we know he remained in Alexandria and became an associate among the great mathematicians who worked there. We do not know much details about his life. His chief work was on the conic sections but he also wrote on other subjects. His mathematical powers were so extraordinary that he became known in his time. His reputation as an astronomer was also great. Apollonius' mathematical works Apollonius is famous for his work, the Conic, which was spread out over eight books and contained 389 propositions. The first four books were 69 in the original Greek language, the next three are preserved in Arabic translations, while the last one is lost. Even though seven of the eight books of the Conics have survived, most of his mathematical work is known today only by titles and summaries in works of later authors. -

The Byzantine Empire (Eastern Roman Empire) Latin
The Byzantine Empire (Eastern Roman Empire) Latin Greek 667 BCE: Greek colonists founded Byzantium 324 CE: Constantine refounded the city as Nova Roma or Constantinople The fall of Rome in 476 ended the western half of Portrait of Constantine, ca. the Roman Empire; the eastern half continued as 315–330 CE. Marble, approx. 8’ the Byzantine Empire, with Constantinople as its 6” high. capital. Early Byzantine Art 6-8th c. The emperor Justinian I ruled the Byzantine Empire from 527 until 565. He is significant for his efforts to regain the lost provinces of the Western Roman Empire, his codification of Roman law, and his architectural achievements. Justinian as world conqueror (Barberini Ivory) Detail: Beardless Christ; Justinian on his horse mid-sixth century. Ivory. The Byzantine Empire , ca 600 Theocracy Government by divine guidance or by officials who are regarded as divinely guided. Justinian as world conqueror (Barberini Ivory), mid-sixth century. Ivory, 1’ 1 1/2” X 10 1/2”. Louvre, Paris. In Orthodox Christianity the central article of faith is the Christ blesses equality of the three aspects the emperor of the Trinity of Father, Son and Holy Spirit. Personificati All other versions of on of Christianity were considered Victory heresies. Personification of Earth Justinian as world conqueror (Barberini Ivory), mid-sixth Barbarians bearing tribute century. Ivory, 1’ 1 1/2” X 10 1/2”. Louvre, Paris. Comparison: Ara Pacis Augustae, Female personification (Tellus; mother earth?), panel from the east facade of the, Rome, Italy, 13–9 BCE. Marble, approx. 5’ 3” high. Comparison: Equestrian statue of Marcus Aurelius, from Rome, Italy, ca.