A Review of Biomass Equations for China's Tree Species
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Abacca Mosaic Virus
Annex Decree of Ministry of Agriculture Number : 51/Permentan/KR.010/9/2015 date : 23 September 2015 Plant Quarantine Pest List A. Plant Quarantine Pest List (KATEGORY A1) I. SERANGGA (INSECTS) NAMA ILMIAH/ SINONIM/ KLASIFIKASI/ NAMA MEDIA DAERAH SEBAR/ UMUM/ GOLONGA INANG/ No PEMBAWA/ GEOGRAPHICAL SCIENTIFIC NAME/ N/ GROUP HOST PATHWAY DISTRIBUTION SYNONIM/ TAXON/ COMMON NAME 1. Acraea acerata Hew.; II Convolvulus arvensis, Ipomoea leaf, stem Africa: Angola, Benin, Lepidoptera: Nymphalidae; aquatica, Ipomoea triloba, Botswana, Burundi, sweet potato butterfly Merremiae bracteata, Cameroon, Congo, DR Congo, Merremia pacifica,Merremia Ethiopia, Ghana, Guinea, peltata, Merremia umbellata, Kenya, Ivory Coast, Liberia, Ipomoea batatas (ubi jalar, Mozambique, Namibia, Nigeria, sweet potato) Rwanda, Sierra Leone, Sudan, Tanzania, Togo. Uganda, Zambia 2. Ac rocinus longimanus II Artocarpus, Artocarpus stem, America: Barbados, Honduras, Linnaeus; Coleoptera: integra, Moraceae, branches, Guyana, Trinidad,Costa Rica, Cerambycidae; Herlequin Broussonetia kazinoki, Ficus litter Mexico, Brazil beetle, jack-tree borer elastica 3. Aetherastis circulata II Hevea brasiliensis (karet, stem, leaf, Asia: India Meyrick; Lepidoptera: rubber tree) seedling Yponomeutidae; bark feeding caterpillar 1 4. Agrilus mali Matsumura; II Malus domestica (apel, apple) buds, stem, Asia: China, Korea DPR (North Coleoptera: Buprestidae; seedling, Korea), Republic of Korea apple borer, apple rhizome (South Korea) buprestid Europe: Russia 5. Agrilus planipennis II Fraxinus americana, -

Common Pines of Massachusetts by GORDON P
Common Pines of Massachusetts by GORDON P. DEWOLF, JR. We tend to take wood for granted; or, if we are very modem, to assume that steel, aluminum, and plastics have made wood obsolete. Such is not the case, and, although wood may not seem very important in a stainless steel and glass office build- ing, it still provides shelter and comfort for most of us. To the English colonists who settled New England, wood was a vital commodity that shaped their future in an alien land. The trees that they encountered were usually in vast tracts, and some were totally different from any they had known in England. - The colonists’ need to clear land for gardens and pastures, combined with the fact that Spain, Portugal and the British West Indies were experiencing a lumber shortage, encouraged the development of a thriving export trade in timber products. White oak barrel staves to make barrels for wine, molasses, and rum were one of the most valuable New England exports. Old England seemed to be interested in only one commodity, how- ever : white pine logs for masts. Until the settlement of the American colonies, Britain had obtained most of her ship building timber either locally or from various ports around the Baltic Sea. With the growth of popu- lation and empire, the numbers and sizes of ships increased. One of the most serious problems for the ship builder was the availability of suitable masts. At the end of the Colonial period a First Rate ship carrying 120 guns required a main mast 40 inches in diameter and 40 yards (120 ft.) long. -

Pines in the Arboretum
UNIVERSITY OF MINNESOTA MtJ ARBORETUM REVIEW No. 32-198 PETER C. MOE Pines in the Arboretum Pines are probably the best known of the conifers native to The genus Pinus is divided into hard and soft pines based on the northern hemisphere. They occur naturally from the up the hardness of wood, fundamental leaf anatomy, and other lands in the tropics to the limits of tree growth near the Arctic characteristics. The soft or white pines usually have needles in Circle and are widely grown throughout the world for timber clusters of five with one vascular bundle visible in cross sec and as ornamentals. In Minnesota we are limited by our cli tions. Most hard pines have needles in clusters of two or three mate to the more cold hardy species. This review will be with two vascular bundles visible in cross sections. For the limited to these hardy species, their cultivars, and a few hy discussion here, however, this natural division will be ignored brids that are being evaluated at the Arboretum. and an alphabetical listing of species will be used. Where neces Pines are readily distinguished from other common conifers sary for clarity, reference will be made to the proper groups by their needle-like leaves borne in clusters of two to five, of particular species. spirally arranged on the stem. Spruce (Picea) and fir (Abies), Of the more than 90 species of pine, the following 31 are or for example, bear single leaves spirally arranged. Larch (Larix) have been grown at the Arboretum. It should be noted that and true cedar (Cedrus) bear their leaves in a dense cluster of many of the following comments and recommendations are indefinite number, whereas juniper (Juniperus) and arborvitae based primarily on observations made at the University of (Thuja) and their related genera usually bear scalelikie or nee Minnesota Landscape Arboretum, and plant performance dlelike leaves that are opposite or borne in groups of three. -

Genetic Diversity and Conservation of Picea Chihuahuana Martínez: a Review
Vol. 13(28), pp. 2786-2795, 9 July, 2014 DOI: 10.5897/AJB2014.13645 Article Number: CADB48845877 ISSN 1684-5315 African Journal of Biotechnology Copyright © 2014 Author(s) retain the copyright of this article http://www.academicjournals.org/AJB Review Genetic diversity and conservation of Picea chihuahuana Martínez: A review Quiñones-Pérez, Carmen Zulema1, Sáenz-Romero, Cuauhtémoc2 and Wehenkel, Christian1* 1Institute of Forestry and Wood Industry, Universidad Juárez del Estado de Durango, Durango, México. 2Institute of Agricultural and Forestry Research, Universidad Michoacana de San Nicolás de Hidalgo, Michoacán, México. Received 20 January, 2014; Accepted 16 June, 2014 The conservation of genetic diversity in tree populations is an essential component of sustainable forest management. Picea chihuahuana Martínez is an endemic conifer species in Mexico and is considered to be endangered. P. chihuahuana covers a total area of no more than 300 ha at the Sierra Madre Occidental, a mountain range that harbor a high diversity of tree species. There are 40 populations of the species that have been identified in the region, and it cannot be found elsewhere. These populations form clusters within gallery forests and are usually associated with eight other tree genera. The P. chihuahuana community is mostly well preserved. Owing to its remarkable characteristics and high conservation value, P. chihuahuana has been the subject of several studies aimed at learning more about the genetic structure, ecology and potential effects of climate change. However, the overall applicability of such studies is to confirm a dataset to develop management tools to help decision makers and to implement preservation and conservation strategies using genetic diversity. -

10. GLOCHIDION J. R. Forster & G. Forster, Char. Gen. Pl. 57. 1775, Nom. Cons
Fl. China 11: 193–202. 2008. 10. GLOCHIDION J. R. Forster & G. Forster, Char. Gen. Pl. 57. 1775, nom. cons. 算盘子属 suan pan zi shu Li Bingtao (李秉滔 Li Ping-tao); Michael G. Gilbert Agyneia Linnaeus; Bradleia Banks ex Gaertner [“Bradleja”]. Trees or shrubs, monoecious, rarely dioecious; indumentum of simple hairs, often absent. Leaves alternate, distichous, or spiral; stipules thick, mostly persistent; petiole short; leaf blade simple, margin entire, venation pinnate. Flowers axillary or supra-axillary, fascicled or in short cymes or umbels, proximal axils with male flowers, distal axils usually with female flowers, usually distinctly pedicellate. Male flowers: pedicels slender or almost absent; sepals 5 or 6, imbricate; petals absent; disk absent; stamens 3–8, connate into an oblong or ellipsoid column, shorter than sepals; anthers 2-locular, extrorse, linear, longitudinally dehiscent, connectives prolonged into an erect acumen; pistillode absent. Female flowers: pedicels stout and short or subsessile; sepals as in male, but slightly thicker; ovary globose, 3–15-locular; ovules 2 per locule; styles connate into a short, thick, cylindric column, apex lobed or toothed, rarely free. Fruit a capsule, globose or depressed globose, ± prominently longitudinally grooved, sunken at apex, dehiscent into 3–15 2-valved cocci when mature, rarely unlobed; exocarp leathery or papery; endocarp crustaceous; styles usually persistent. Seeds not strophiolate, hemispheric or laterally compressed; endosperm fleshy; cotyledon flattened. About 200 species: chiefly in tropical Asia, the Pacific islands, and Malaysia, a few in tropical America and Africa; 28 species (seven endemic, one introduced) in China. Glochidion is noteworthy for its pollination mechanism, which involves a symbiotic relationship with moths of the genus Epicephala closely paralleling that found in Yucca (Kato et al., Proc. -

Effect of Pine Fruits on Some Biological Changes in Hypercholesterolemia
Effect of pine fruits on some biological changes in hypercholesterolemia rats induced Omar Ahmed Emam, Ahmed Mohamed Gaafer , Ghada Mahmoud Elbassiony and Mashael Mobard Ahmed El-Fadly Effect of pine fruits on some biological changes in hypercholesterolemia rats induced Omar Ahmed Emam1, Ahmed Mohamed Gaafer2, Ghada Mahmoud Elbassiony1 and Mashael Mobard Ahmed El-Fadly1 1Department of Home Economics, Faculty of Specific Education, Benha University, Benha, Egypt; 2Research Institute of Food Technology , Agricultural Research Center, Giza, Egypt Abstract his study aimed to determine chemical composition, antioxidant contents, fatty acids of pine nut fruits and also, the effect of pine powder with different ratio T (3, 6 and 9%) on biochemical changes of hypercholesterolemic rats. Biological evaluation of growth performance, Lipid profile, serum protein, blood sugars, liver and kidney functions were also studied. The obtained results indicated that pine nut fruits are considered as a good source of oils, crude fibers, ash, protein, soluble carbohydrates, total energy polyphenols and flavonoids. Besides, it is a rich source of unsaturated fatty acids mainly, linoleic acid (C18:2) which represent more than half amount of total fatty acids. Biological evaluations showed that pine nut was significantly decreased (P ≤ 0.05) of body weight, total lipids, triglycerides, LDL, HDL, VLDL cholesterol of serum hypercholesterolemic rats as compared with positive group of rats Also, it caused significant decrease (P ≤ 0.05) in liver enzyme (AST, ALT and ALP) and kidney parameters (urea, uric acid and creatinine, i.e. improved liver and kidney functions as compared with positive control group. Meanwhile, both total protein and albumin were increased. -
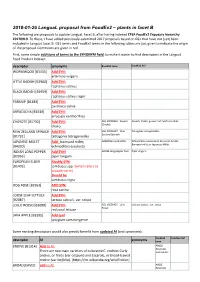
2018-01-26 Langual Proposal from Foodex2 – Plants in Facet B
2018-01-26 LanguaL proposal from FoodEx2 – plants in facet B The following are proposals to update LanguaL Facet B, after having indexed EFSA FoodEx2 Exposure hierarchy 20170919. To these, I have added previously-submitted 2017 proposals based on GS1 that have not (yet) been included in LanguaL facet B. GS1 terms and FoodEx2 terms in the following tables are just given to indicate the origin of the proposal. Comments are given in red. First, some simple additions of terms to the SYNONYM field, to make it easier to find descriptors in the LanguaL Food Product Indexer: descriptor synonyms FoodEx2 term FoodEx2 def WORMWOOD [B3433] Add SYN: artemisia vulgaris LITTLE RADISH [B2960] Add SYN: raphanus sativus BLACK RADISH [B2959] Add SYN: raphanus sativus niger PARSNIP [B1483] Add SYN: pastinaca sativa ARRACACHA [B3439] Add SYN: arracacia xanthorrhiza CHAYOTE [B1730] Add SYN: GS1 10006356 - Squash Squash, Choko, grown from Sechium edule (Choko) choko NEW ZEALAND SPINACH Add SYN: GS1 10006427 - New- Tetragonia tetragonoides Zealand Spinach [B1732] tetragonia tetragonoides JAPANESE MILLET Add : barnyard millet; A000Z Barnyard millet Echinochloa esculenta (A. Braun) H. Scholz, Barnyard millet or Japanese Millet. [B4320] echinochloa esculenta INDIAN LONG PEPPER Add SYN! A019B Long pepper fruit Piper longum [B2956] piper longum EUROPEAN ELDER Modify SYN: [B1403] sambucus spp. (which refers to broader term) Should be sambucus nigra DOG ROSE [B2961] ADD SYN: rosa canina LOOSE LEAF LETTUCE Add SYN: [B2087] lactusa sativa L. var. crispa LOLLO ROSSO [B2088] Add SYN: GS1 10006425 - Lollo Lactuca sativa L. var. crispa Rosso red coral lettuce JAVA APPLE [B3395] Add syn! syzygium samarangense Some existing descriptors would also greatly benefit from updated AI (and synonyms): FoodEx2 FoodEx2 def descriptor AI synonyms term ENDIVE [B1314] Add to AI: A00LD Escaroles There are two main varieties of cultivated C. -

(Orthoptera, Caelifera, Acrididae) on the Subfamily Level Using Molecular Markers
e-ISSN 1734-9168 Folia Biologica (Kraków), vol. 67 (2019), No 3 http://www.isez.pan.krakow.pl/en/folia-biologica.html https://doi.org/10.3409/fb_67-3.12 The Evaluation of Genetic Relationships within Acridid Grasshoppers (Orthoptera, Caelifera, Acrididae) on the Subfamily Level Using Molecular Markers Igor SUKHIKH , Kirill USTYANTSEV , Alexander BUGROV, Michael SERGEEV, Victor FET, and Alexander BLINOV Accepted August 20, 2019 Published online September 11, 2019 Issue online September 30, 2019 Original article SUKHIKH I., USTYANTSEV K., BUGROV A., SERGEEV M., FET V., BLINOV A. 2019. The evaluation of genetic relationships within Acridid grasshoppers (Orthoptera, Caelifera, Acrididae) on the subfamily level using molecular markers. Folia Biologica (Kraków) 67: 119-126. Over the last few decades, molecular markers have been extensively used to study phylogeny, population dynamics, and genome mapping in insects and other taxa. Phylogenetic methods using DNA markers are inexpensive, fast and simple to use, and may help greatly to resolve phylogenetic relationships in groups with problematic taxonomy. However, different markers have various levels of phylogenetic resolution, and it’s important to choose the right set of molecular markers for a studied taxonomy level. Acrididae is the most diverse family of grasshoppers. Many attempts to resolve the phylogenetic relationships within it did not result in a clear picture, partially because of the limited number of molecular markers used. We have tested a phylogenetic resolution of three sets of the most commonly utilized mitochondrial molecular markers available for Acrididae sequences in the database: (i) complete protein-coding mitochondrial sequences, (ii) concatenated mitochondrial genes COI, COII, and Cytb, and (iii) concatenated mitochondrial genes COI and COII. -

Assessment and Conservation of Threatened Bird Species at Laojunshan, Sichuan, China
CLP Report Assessment and conservation of threatened bird species at Laojunshan, Sichuan, China Submitted by Jie Wang Institute of Zoology, Chinese Academy of Sciences, Beijing, P.R.China E-mail:[email protected] To Conservation Leadership Programme, UK Contents 1. Summary 2. Study area 3. Avian fauna and conservation status of threatened bird species 4. Habitat analysis 5. Ecological assessment and community education 6. Outputs 7. Main references 8. Acknowledgements 1. Summary Laojunshan Nature Reserve is located at Yibin city, Sichuan province, south China. It belongs to eastern part of Liangshan mountains and is among the twenty-five hotspots of global biodiversity conservation. The local virgin alpine subtropical deciduous forests are abundant, which are actually rare at the same latitudes and harbor a tremendous diversity of plant and animal species. It is listed as a Global 200 ecoregion (WWF), an Important Bird Area (No. CN205), and an Endemic Bird Area (No. D14) (Stattersfield, et al . 1998). However, as a nature reserve newly built in 1999, it is only county-level and has no financial support from the central government. Especially, it is quite lack of scientific research, for example, the avifauna still remains unexplored except for some observations from bird watchers. Furthermore, the local community is extremely poor and facing modern development pressures, unmanaged human activities might seriously disturb the local ecosystem. We conducted our project from April to June 2007, funded by Conservation Leadership Programme. Two fieldwork strategies were used: “En bloc-Assessment” to produce an avifauna census and ecological assessments; "Special Survey" to assess the conservation status of some threatened endemic bird species. -

Chapter 4 Phytogeography of Northeast Asia
Chapter 4 Phytogeography of Northeast Asia Hong QIAN 1, Pavel KRESTOV 2, Pei-Yun FU 3, Qing-Li WANG 3, Jong-Suk SONG 4 and Christine CHOURMOUZIS 5 1 Research and Collections Center, Illinois State Museum, 1011 East Ash Street, Springfield, IL 62703, USA, e-mail: [email protected]; 2 Institute of Biology and Soil Science, Russian Academy of Sciences, Vladivostok, 690022, Russia, e-mail: [email protected]; 3 Institute of Applied Ecology, Chinese Academy of Sciences, P.O. Box 417, Shenyang 110015, China; 4 Department of Biological Science, College of Natural Sciences, Andong National University, Andong 760-749, Korea, e-mail: [email protected]; 5 Department of Forest Sciences, University of British Columbia, 3041-2424 mail Mall, Vancouver, B.C., V6T 1Z4, Canada, e-mail: [email protected] Abstract: Northeast Asia as defined in this study includes the Russian Far East, Northeast China, the northern part of the Korean Peninsula, and Hokkaido Island (Japan). We determined the species richness of Northeast Asia at various spatial scales, analyzed the floristic relationships among geographic regions within Northeast Asia, and compared the flora of Northeast Asia with surrounding floras. The flora of Northeast Asia consists of 971 genera and 4953 species of native vascular plants. Based on their worldwide distributions, the 971 gen- era were grouped into fourteen phytogeographic elements. Over 900 species of vascular plants are endemic to Northeast Asia. Northeast Asia shares 39% of its species with eastern Siberia-Mongolia, 24% with Europe, 16.2% with western North America, and 12.4% with eastern North America. -

Grasshoppers and Locusts (Orthoptera: Caelifera) from the Palestinian Territories at the Palestine Museum of Natural History
Zoology and Ecology ISSN: 2165-8005 (Print) 2165-8013 (Online) Journal homepage: http://www.tandfonline.com/loi/tzec20 Grasshoppers and locusts (Orthoptera: Caelifera) from the Palestinian territories at the Palestine Museum of Natural History Mohammad Abusarhan, Zuhair S. Amr, Manal Ghattas, Elias N. Handal & Mazin B. Qumsiyeh To cite this article: Mohammad Abusarhan, Zuhair S. Amr, Manal Ghattas, Elias N. Handal & Mazin B. Qumsiyeh (2017): Grasshoppers and locusts (Orthoptera: Caelifera) from the Palestinian territories at the Palestine Museum of Natural History, Zoology and Ecology, DOI: 10.1080/21658005.2017.1313807 To link to this article: http://dx.doi.org/10.1080/21658005.2017.1313807 Published online: 26 Apr 2017. Submit your article to this journal View related articles View Crossmark data Full Terms & Conditions of access and use can be found at http://www.tandfonline.com/action/journalInformation?journalCode=tzec20 Download by: [Bethlehem University] Date: 26 April 2017, At: 04:32 ZOOLOGY AND ECOLOGY, 2017 https://doi.org/10.1080/21658005.2017.1313807 Grasshoppers and locusts (Orthoptera: Caelifera) from the Palestinian territories at the Palestine Museum of Natural History Mohammad Abusarhana, Zuhair S. Amrb, Manal Ghattasa, Elias N. Handala and Mazin B. Qumsiyeha aPalestine Museum of Natural History, Bethlehem University, Bethlehem, Palestine; bDepartment of Biology, Jordan University of Science and Technology, Irbid, Jordan ABSTRACT ARTICLE HISTORY We report on the collection of grasshoppers and locusts from the Occupied Palestinian Received 25 November 2016 Territories (OPT) studied at the nascent Palestine Museum of Natural History. Three hundred Accepted 28 March 2017 and forty specimens were collected during the 2013–2016 period. -

Number 3, Spring 1998 Director’S Letter
Planning and planting for a better world Friends of the JC Raulston Arboretum Newsletter Number 3, Spring 1998 Director’s Letter Spring greetings from the JC Raulston Arboretum! This garden- ing season is in full swing, and the Arboretum is the place to be. Emergence is the word! Flowers and foliage are emerging every- where. We had a magnificent late winter and early spring. The Cornus mas ‘Spring Glow’ located in the paradise garden was exquisite this year. The bright yellow flowers are bright and persistent, and the Students from a Wake Tech Community College Photography Class find exfoliating bark and attractive habit plenty to photograph on a February day in the Arboretum. make it a winner. It’s no wonder that JC was so excited about this done soon. Make sure you check of themselves than is expected to seedling selection from the field out many of the special gardens in keep things moving forward. I, for nursery. We are looking to propa- the Arboretum. Our volunteer one, am thankful for each and every gate numerous plants this spring in curators are busy planting and one of them. hopes of getting it into the trade. preparing those gardens for The magnolias were looking another season. Many thanks to all Lastly, when you visit the garden I fantastic until we had three days in our volunteers who work so very would challenge you to find the a row of temperatures in the low hard in the garden. It shows! Euscaphis japonicus. We had a twenties. There was plenty of Another reminder — from April to beautiful seven-foot specimen tree damage to open flowers, but the October, on Sunday’s at 2:00 p.m.