DOCSLIB.ORG

Paper Folding and Polyhedron

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Paper Folding and Polyhedron Paper Folding and Polyhedron Ashley Shimabuku 8 December 2010 1 Introduction There is a connection between the art of folding paper and mathematics. Paper folding is a beautiful and intricate art form that has existed for thousands of years. Origami is a great example of something people generally consider to be non-mathematical to have hidden math aspects. Origami folding has recently found practical applications in industry. Car companies have been trying to find the best way to fold the airbag up into the dashboard that will provide the fastest and most efficient unfolding upon impact. Geneticist have been looking at folding to help them think about DNA strands and protein chains [2]. There is an assortment of paper folding activities concerning geometry. However, some of my students at the Thurgood Marshall Academic High School Math Circle have not taken a geometry class. This activity is accessible to grade levels 8 − 12. This activity is designed so that all the students can participate and the instructors do not have to worry about the different levels of mathematical ability. The activity is based around a shape called a Sonobe unit from [1]. Figure 1: Sonobe unit A Sonobe unit is a very basic shape and is easy to make quickly. Using several of these Sonobe units we can construct polyhedra. Students of all mathematical abilities will be 1 Ashley Shimabuku Paper Folding and Polyhedron Math 728 able to recognize and understand these basic three-dimensional objects. And from this basic polyhedron we can talk with the students about counting and coloring. I think that the students will have fun figuring out the connection between the number of Sonobe units and faces of polyhedron and how to piece together the Sonobe units to color the polyhedron in a certain way. 2 Learning Objectives We will start the activity with a shape called a Sonobe unit. A Sonobe unit is a simple shape requiring only a dozen folds to construct. Although it is simple we can use several of them to build a three-dimensional polyhedron. Starting with only six Sonobe units we will construct a cube. After constructing a cube we can ask mathematical questions about its construction and coloring. 3 Materials Required 1. Origami paper 2. Diagram on how to make a Sonobe unit 3. Example of a constructed cube 4 Mathematical Background Definitions: • A polyhedron is a three dimensional solid with straight faces and edges. • A vertex is a corner of the polyhedron. • An edge of a polyhedron is a line that connects two vertices. • A face of a polyhedron is the two dimensional polygon created by the edges. • A cube is a three dimensional solid with 6 square faces, 8 vertices and 12 edges. The origami cube is picture in Figure 2a. • An octahedron is a three dimensional solid with 8 faces, where three squares meet at a vertex. The cube has 8 vertices and 12 edges. • An icosahedron is a three dimensional solid with 20 faces, 12 vertices and 30 edges. 2 Ashley Shimabuku Paper Folding and Polyhedron Math 728 • Stellate means to make or form into a star. • A stellated octahedron is an octahedron with a triangular pyramid on each face. The origami stellated octahedron is picture in Figure 2b. • A stellated icosahedron is an icosahedron with a triangular pyramid on each face. The origami stellated iscosahderon is picture in Figure 2c. • A polyhedron is n-colorable if there is a way to construct the polyhedra from n different colored Sonobe units where no Sonobe of the same color are inserted into each other. 5 Examples (a) Cube (b) Stellated Octohedron (c) Stellated Iscosahedron Figure 2: Examples of constructed polyhedron 6 Lesson Plan This lesson plan may need to be done over two class periods. The lesson will begin with a classroom introduction to the Sonobe unit. The folding and construction part of the activity can be done in groups. 1. We will begin with an introduction to the Sonobe unit. Each table should have a copy of the instruction sheet. The instructions are clear but some of the students may have a hard time associating the pictures to the physically folding their own paper. We will take the class step by step through the construction. They will need to make six Sonobe units to make a cube. 2. Have the students work in groups to finish their Sonobe units and build a cube. While the students are making all of their Sonobe units the ones having difficultly will get a chance to watch their peers. The handout has questions about the cube. They can also make and talk about the stellated octahedron and stellated icosahedron. 3 Ashley Shimabuku Paper Folding and Polyhedron Math 728 3. After the students have built a their own cube and have talked through some of the question on the handout we'll bring the class back together to introduce coloring. A cube is 3-colorable. 4. The students can get back in their groups to talk about what it means to be colorable. There are questions about this topic on the handout. 5. If students finish early, they can talk about coloring a stellated octahedron and stellated icosahedron in their groups. 6. The last part of the lesson will be a class discussion about the following topics. (a) What kinds of polyhedron were you able to make? (b) What were your favorite polyhedron? (c) Was a cube 2-colorable? What polyhedron were 3-colorable? (d) Did you expect to find math while doing origami? 7 Teacher's Reflection The activity went very well in Math Circle. All of the students were engaged and asking questions about how to construct the cube. Almost everyone made their own cube and a few of them were able to make the stellated octahedron with minimal guidance. The students enjoyed constructing something they could bring home and show their family. Even the teachers enjoyed making the cubes and one of the TMAHS teachers was interested in using this activity in her own class. My partner teacher and I did the first part of the lesson plan with his Algebra Project class and his freshmen algebra class. We wanted to see how difficult it would be for them to build a cube. Some of the students only needed a short introduction and were able to build their own cubes quite quickly. Others were much slower at understanding how to fold the Sonobe unit. We found that the third and ninth step in the instruction sheet on building the Sonobe unit was hardest for the students. These steps needed special attention. My partner teacher and I decided the best thing for Math Circle would be to have the students pair up and work on one cube between them. This plan would hopefully save some time and enable the students to start answering questions on the worksheet. However, this plan did not work very well in Math Circle. All the students, except for the junior high students, wanted to make their own cubes. The students were so focused on building their own cubes that they completely ignored the worksheet that went along with it. We realized that this project is best done over two days. One day to build the cube and get used to the Sonobe units and another day to ask questions about the cube. 4 Ashley Shimabuku Paper Folding and Polyhedron Math 728 8 References 1. http://riverbendmath.org/modules/Origami/Sonobe_Polyhedra/info 2. http://nuwen.net/poly.html 3. "Between the Folds": PBS documentary, http://www.greenfusefilms.com/ 5 Questions and Challenges: 1. How many Sonobe units does it take to build a cube? 2. What is the least number of Sonobe units you need to make a polyhedron? Can you make a polyhedron from 1 Sonobe unit? 3. What other polyhedron can you make? 4. A stellated octahedron is a three dimensional solid with 8 triangular faces, 8 vertices and 12 edges. How many Sonobe units would you need to build a stellated octahedron? A stellated icosahedron? 5. Can you construct a cube that is 3-colorable? 2-colorable? 6. Can you construct a polyhedron with a 2-coloring? How about something other than a cube with a 3-coloring? 6 Further Questions: 1. A polyhedron is n-colorable if there is a way to construct the polyhedron from n different colored Sonobe units where no Sonobe of the same color are inserted into each other. Can you construct a polyhedron that is 4-colorable? 2. Can you construct a stellated octahedron with a 3-Coloring? How about a stellated icosahedron? 3. Not all polyhedrons are 3-colorable. Can you construct a polyhedron without a 3- Coloring? How about 4-Coloring? 7 e e not mak mak dules do to mo also — folds wn o six lines do w t olyhedra dules p last crease mo triangles requires other the e e the triangles er y cub old F Undo A cross sharp Sonob man Directions/ Figure 3: to to left in up fit lines the ottom b dule http://riverbendmath.org/modules/Origami/Sonobe_Polyhedra/Activity_ corner let t mo crease and not t righ one do another cross righ of of — ottom top b Units ets edge k c o old old F F Corners corners left p triangles Origami to to and e wn crease wn line do sho er, v as ter o Sonob dule cen er corner mo lines to pap left the the dashed edge top edges t 8 urn old old F F T along righ unfold complete lines under middle corner and t the crease corner side righ wn er do left w ertical osite er v lo er opp pap for upp along on unfold k eat uc old rep flap Crease F T and.
Load more

Recommended publications
  • Equivelar Octahedron of Genus 3 in 3-Space
    Equivelar octahedron of genus 3 in 3-space Ruslan Mizhaev ([email protected]) Apr. 2020 ABSTRACT . Building up a toroidal polyhedron of genus 3, consisting of 8 nine-sided faces, is given. From the point of view of topology, a polyhedron can be considered as an embedding of a cubic graph with 24 vertices and 36 edges in a surface of genus 3. This polyhedron is a contender for the maximal genus among octahedrons in 3-space. 1. Introduction This solution can be attributed to the problem of determining the maximal genus of polyhedra with the number of faces - . As is known, at least 7 faces are required for a polyhedron of genus = 1 . For cases ≥ 8 , there are currently few examples. If all faces of the toroidal polyhedron are – gons and all vertices are q-valence ( ≥ 3), such polyhedral are called either locally regular or simply equivelar [1]. The characteristics of polyhedra are abbreviated as , ; [1]. 2. Polyhedron {9, 3; 3} V1. The paper considers building up a polyhedron 9, 3; 3 in 3-space. The faces of a polyhedron are non- convex flat 9-gons without self-intersections. The polyhedron is symmetric when rotated through 1804 around the axis (Fig. 3). One of the features of this polyhedron is that any face has two pairs with which it borders two edges. The polyhedron also has a ratio of angles and faces - = − 1. To describe polyhedra with similar characteristics ( = − 1) we use the Euler formula − + = = 2 − 2, where is the Euler characteristic. Since = 3, the equality 3 = 2 holds true.
    [Show full text]
  • Archimedean Solids
    University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of Nebraska-Lincoln Follow this and additional works at: https://digitalcommons.unl.edu/mathmidexppap Part of the Science and Mathematics Education Commons Anderson, Anna, "Archimedean Solids" (2008). MAT Exam Expository Papers. 4. https://digitalcommons.unl.edu/mathmidexppap/4 This Article is brought to you for free and open access by the Math in the Middle Institute Partnership at DigitalCommons@University of Nebraska - Lincoln. It has been accepted for inclusion in MAT Exam Expository Papers by an authorized administrator of DigitalCommons@University of Nebraska - Lincoln. Archimedean Solids Anna Anderson In partial fulfillment of the requirements for the Master of Arts in Teaching with a Specialization in the Teaching of Middle Level Mathematics in the Department of Mathematics. Jim Lewis, Advisor July 2008 2 Archimedean Solids A polygon is a simple, closed, planar figure with sides formed by joining line segments, where each line segment intersects exactly two others. If all of the sides have the same length and all of the angles are congruent, the polygon is called regular. The sum of the angles of a regular polygon with n sides, where n is 3 or more, is 180° x (n – 2) degrees. If a regular polygon were connected with other regular polygons in three dimensional space, a polyhedron could be created. In geometry, a polyhedron is a three- dimensional solid which consists of a collection of polygons joined at their edges. The word polyhedron is derived from the Greek word poly (many) and the Indo-European term hedron (seat).
    [Show full text]
  • How to Make an Origami Octahedron Ball
    How to make an Origami Octahedron Ball Introduction: These instructions will teach you how to make an origami octahedron. The ball is constructed by assembling 12 folded units together. A unit This is called a Sonobe unit, named after the person who invented them. The process of using identical units and assembling them in a pattern to create large, complex, beautiful structures is considered modular origami. This type of origami requires multiple sheets of paper to make a model. By varying the number of units, you can make several other shapes. A cube requires 6 units and an icosahedron requires 30. Time Frame: 30 minutes Materials: 2- 8.5”x11” sheets of paper (Multi-colored ball: use 3 different colored sheets of paper) Scissors Ruler (measures inches) Pencil Preparation: Make sure you have enough space and a flat surface to fold the origami. Procedure: Step 1. Cut 12 – 3”x3” square pieces of paper Note: The size of the squares depends on your preference of how large you want the ball to be. These instructions create a ball that fits in your hand. To save time, origami squares (4”x4”) can be used and step 1 skipped. 1.1. Draw 6 squares that are 3”x3” on a sheet of paper with the pencil and ruler. Note: For a multi-color effect, as depicted in these instructions, use 3 different colors of paper and cut 4 squares from each. 1.2.Stack the second sheet of paper behind the first. 1.3. Cut out 12 squares of paper with the scissors.
    [Show full text]
  • Shape Skeletons Creating Polyhedra with Straws
    Shape Skeletons Creating Polyhedra with Straws Topics: 3-Dimensional Shapes, Regular Solids, Geometry Materials List Drinking straws or stir straws, cut in Use simple materials to investigate regular or advanced 3-dimensional shapes. half Fun to create, these shapes make wonderful showpieces and learning tools! Paperclips to use with the drinking Assembly straws or chenille 1. Choose which shape to construct. Note: the 4-sided tetrahedron, 8-sided stems to use with octahedron, and 20-sided icosahedron have triangular faces and will form sturdier the stir straws skeletal shapes. The 6-sided cube with square faces and the 12-sided Scissors dodecahedron with pentagonal faces will be less sturdy. See the Taking it Appropriate tool for Further section. cutting the wire in the chenille stems, Platonic Solids if used This activity can be used to teach: Common Core Math Tetrahedron Cube Octahedron Dodecahedron Icosahedron Standards: Angles and volume Polyhedron Faces Shape of Face Edges Vertices and measurement Tetrahedron 4 Triangles 6 4 (Measurement & Cube 6 Squares 12 8 Data, Grade 4, 5, 6, & Octahedron 8 Triangles 12 6 7; Grade 5, 3, 4, & 5) Dodecahedron 12 Pentagons 30 20 2-Dimensional and 3- Dimensional Shapes Icosahedron 20 Triangles 30 12 (Geometry, Grades 2- 12) 2. Use the table and images above to construct the selected shape by creating one or Problem Solving and more face shapes and then add straws or join shapes at each of the vertices: Reasoning a. For drinking straws and paperclips: Bend the (Mathematical paperclips so that the 2 loops form a “V” or “L” Practices Grades 2- shape as needed, widen the narrower loop and insert 12) one loop into the end of one straw half, and the other loop into another straw half.
    [Show full text]
  • VOLUME of POLYHEDRA USING a TETRAHEDRON BREAKUP We
    VOLUME OF POLYHEDRA USING A TETRAHEDRON BREAKUP We have shown in an earlier note that any two dimensional polygon of N sides may be broken up into N-2 triangles T by drawing N-3 lines L connecting every second vertex. Thus the irregular pentagon shown has N=5,T=3, and L=2- With this information, one is at once led to the question-“ How can the volume of any polyhedron in 3D be determined using a set of smaller 3D volume elements”. These smaller 3D eelements are likely to be tetrahedra . This leads one to the conjecture that – A polyhedron with more four faces can have its volume represented by the sum of a certain number of sub-tetrahedra. The volume of any tetrahedron is given by the scalar triple product |V1xV2∙V3|/6, where the three Vs are vector representations of the three edges of the tetrahedron emanating from the same vertex. Here is a picture of one of these tetrahedra- Note that the base area of such a tetrahedron is given by |V1xV2]/2. When this area is multiplied by 1/3 of the height related to the third vector one finds the volume of any tetrahedron given by- x1 y1 z1 (V1xV2 ) V3 Abs Vol = x y z 6 6 2 2 2 x3 y3 z3 , where x,y, and z are the vector components. The next question which arises is how many tetrahedra are required to completely fill a polyhedron? We can arrive at an answer by looking at several different examples. Starting with one of the simplest examples consider the double-tetrahedron shown- It is clear that the entire volume can be generated by two equal volume tetrahedra whose vertexes are placed at [0,0,sqrt(2/3)] and [0,0,-sqrt(2/3)].
    [Show full text]
  • Sonobe Origami Units
    Sonobe Origami Units Crease paper down the middle Fold edges to center line and Fold top right and bottom left Fold triangles down to make and unfold unfold corners | do not let the sharper triangles | do not triangles cross crease lines cross the crease lines Fold along vertical crease lines Fold top left corner down to Fold bottom right corner up to Undo the last two folds right edge left edge Tuck upper left corner under Turn the paper over, crease Corners of one module ¯t into along dashed lines as shown to flap on opposite side and pockets of another A cube requires six modules repeat for lower right corner complete the module Sonobe modules also make many other polyhedra Where's the Math in Origami? Origami may not seem like it involves very much mathematics. Yes, origami involves symmetry. If we build a polyhedron then, sure, we encounter a shape from geometry. Is that as far as it goes? Do any interesting mathematical questions arise from the process of folding paper? Is there any deep mathematics in origami? Is the mathematics behind origami useful for anything other than making pretty decorations? People who spend time folding paper often ask themselves questions that are ultimately mathematical in nature. Is there a simpler procedure for folding a certain ¯gure? Where on the original square paper do the wings of a crane come from? What size paper should I use to make a chair to sit at the origami table I already made? Is it possible to make an origami beetle that has six legs and two antennae from a single square sheet of paper? Is there a precise procedure for folding a paper into ¯ve equal strips? In the last few decades, folders inspired by questions like these have revolutionized origami by bringing mathematical techniques to their art.
    [Show full text]
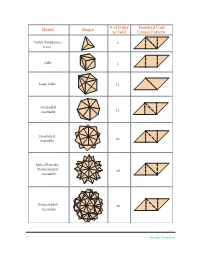
  • Sonobe Assembly Guide for a Few Polyhedra
    Model Shape # of Units Finished Unit to Fold Crease Pattern Toshie Takahama’s 3 Jewel Cube 6 Large Cube 12 Octahedral Assembly 12 Icosahedral Assembly 30 Spiked Pentakis Dodecahedral 60 Assembly Dodecahedral 90 Assembly 2 Sonobe Variations Sonobe Assembly Basics Sonobe assemblies are essentially “pyramidized” constructing a polyhedron, the key thing to re- polyhedra, each pyramid consisting of three So- member is that the diagonal ab of each Sonobe nobe units. The figure below shows a generic So- unit will lie along an edge of the polyhedron. nobe unit and how to form one pyramid. When a Pocket Tab Forming one Tab pyramid Pocket b A generic Sonobe unit representation Sonobe Assembly Guide for a Few Polyhedra 1. Toshie’s Jewel: Crease three finished units as tabs and pockets. This assembly is also sometimes explained in the table on page 2. Form a pyramid known as a Crane Egg. as above. Then turn the assembly upside down 2. Cube Assembly: Crease six finished units as and make another pyramid with the three loose explained in the table on page 2. Each face will be made up of 3 the center square of one unit and the tabs of two other units. 4 Do Steps 1 and 2 to form one face. Do Steps 3 and 4 to form one corner or vertex. Continue 1 2 interlocking in this manner to arrive at the finished cube. Sonobe Variations 3 3. Large Cube Assembly: Crease 12 finished units as explained on page 2. 5 6 3 The 12-unit large cube is the only assembly that does not involve pyramidizing.
    [Show full text]
  • Polyhedral Harmonics
    value is uncertain; 4 Gr a y d o n has suggested values of £estrap + A0 for the first three excited 4,4 + 0,1 v. e. states indicate 11,1 v.e. för D0. The value 6,34 v.e. for Dextrap for SO leads on A rough correlation between Dextrap and bond correction by 0,37 + 0,66 for the'valence states of type is evident for the more stable states of the the two atoms to D0 ^ 5,31 v.e., in approximate agreement with the precisely known value 5,184 v.e. diatomic molecules. Thus the bonds A = A and The valence state for nitrogen, at 27/100 F2 A = A between elements of the first short period (with 2D at 9/25 F2 and 2P at 3/5 F2), is calculated tend to have dissociation energy to the atomic to lie about 1,67 v.e. above the normal state, 4S, valence state equal to about 6,6 v.e. Examples that for the iso-electronic oxygen ion 0+ is 2,34 are 0+ X, 6,51; N2 B, 6,68; N2 a, 6,56; C2 A, v.e., and that for phosphorus is 1,05 v.e. above 7,05; C2 b, 6,55 v.e. An increase, presumably due their normal states. Similarly the bivalent states to the stabilizing effect of the partial ionic cha- of carbon, : C •, the nitrogen ion, : N • and racter of the double bond, is observed when the atoms differ by 0,5 in electronegativity: NO X, Silicon,:Si •, are 0,44 v.e., 0,64 v.e., and 0,28 v.e., 7,69; CN A, 7,62 v.e.
    [Show full text]
  • Arxiv:1705.01294V1
    Branes and Polytopes Luca Romano email address: [email protected] ABSTRACT We investigate the hierarchies of half-supersymmetric branes in maximal supergravity theories. By studying the action of the Weyl group of the U-duality group of maximal supergravities we discover a set of universal algebraic rules describing the number of independent 1/2-BPS p-branes, rank by rank, in any dimension. We show that these relations describe the symmetries of certain families of uniform polytopes. This induces a correspondence between half-supersymmetric branes and vertices of opportune uniform polytopes. We show that half-supersymmetric 0-, 1- and 2-branes are in correspondence with the vertices of the k21, 2k1 and 1k2 families of uniform polytopes, respectively, while 3-branes correspond to the vertices of the rectified version of the 2k1 family. For 4-branes and higher rank solutions we find a general behavior. The interpretation of half- supersymmetric solutions as vertices of uniform polytopes reveals some intriguing aspects. One of the most relevant is a triality relation between 0-, 1- and 2-branes. arXiv:1705.01294v1 [hep-th] 3 May 2017 Contents Introduction 2 1 Coxeter Group and Weyl Group 3 1.1 WeylGroup........................................ 6 2 Branes in E11 7 3 Algebraic Structures Behind Half-Supersymmetric Branes 12 4 Branes ad Polytopes 15 Conclusions 27 A Polytopes 30 B Petrie Polygons 30 1 Introduction Since their discovery branes gained a prominent role in the analysis of M-theories and du- alities [1]. One of the most important class of branes consists in Dirichlet branes, or D-branes. D-branes appear in string theory as boundary terms for open strings with mixed Dirichlet-Neumann boundary conditions and, due to their tension, scaling with a negative power of the string cou- pling constant, they are non-perturbative objects [2].
    [Show full text]
  • The Geometry Junkyard: Origami
    Table of Contents Table of Contents 1 Origami 2 Origami The Japanese art of paper folding is obviously geometrical in nature. Some origami masters have looked at constructing geometric figures such as regular polyhedra from paper. In the other direction, some people have begun using computers to help fold more traditional origami designs. This idea works best for tree-like structures, which can be formed by laying out the tree onto a paper square so that the vertices are well separated from each other, allowing room to fold up the remaining paper away from the tree. Bern and Hayes (SODA 1996) asked, given a pattern of creases on a square piece of paper, whether one can find a way of folding the paper along those creases to form a flat origami shape; they showed this to be NP-complete. Related theoretical questions include how many different ways a given pattern of creases can be folded, whether folding a flat polygon from a square always decreases the perimeter, and whether it is always possible to fold a square piece of paper so that it forms (a small copy of) a given flat polygon. Krystyna Burczyk's Origami Gallery - regular polyhedra. The business card Menger sponge project. Jeannine Mosely wants to build a fractal cube out of 66048 business cards. The MIT Origami Club has already made a smaller version of the same shape. Cardahedra. Business card polyhedral origami. Cranes, planes, and cuckoo clocks. Announcement for a talk on mathematical origami by Robert Lang. Crumpling paper: states of an inextensible sheet. Cut-the-knot logo.
    [Show full text]
  • 15 BASIC PROPERTIES of CONVEX POLYTOPES Martin Henk, J¨Urgenrichter-Gebert, and G¨Unterm
    15 BASIC PROPERTIES OF CONVEX POLYTOPES Martin Henk, J¨urgenRichter-Gebert, and G¨unterM. Ziegler INTRODUCTION Convex polytopes are fundamental geometric objects that have been investigated since antiquity. The beauty of their theory is nowadays complemented by their im- portance for many other mathematical subjects, ranging from integration theory, algebraic topology, and algebraic geometry to linear and combinatorial optimiza- tion. In this chapter we try to give a short introduction, provide a sketch of \what polytopes look like" and \how they behave," with many explicit examples, and briefly state some main results (where further details are given in subsequent chap- ters of this Handbook). We concentrate on two main topics: • Combinatorial properties: faces (vertices, edges, . , facets) of polytopes and their relations, with special treatments of the classes of low-dimensional poly- topes and of polytopes \with few vertices;" • Geometric properties: volume and surface area, mixed volumes, and quer- massintegrals, including explicit formulas for the cases of the regular simplices, cubes, and cross-polytopes. We refer to Gr¨unbaum [Gr¨u67]for a comprehensive view of polytope theory, and to Ziegler [Zie95] respectively to Gruber [Gru07] and Schneider [Sch14] for detailed treatments of the combinatorial and of the convex geometric aspects of polytope theory. 15.1 COMBINATORIAL STRUCTURE GLOSSARY d V-polytope: The convex hull of a finite set X = fx1; : : : ; xng of points in R , n n X i X P = conv(X) := λix λ1; : : : ; λn ≥ 0; λi = 1 : i=1 i=1 H-polytope: The solution set of a finite system of linear inequalities, d T P = P (A; b) := x 2 R j ai x ≤ bi for 1 ≤ i ≤ m ; with the extra condition that the set of solutions is bounded, that is, such that m×d there is a constant N such that jjxjj ≤ N holds for all x 2 P .
    [Show full text]
  • What Is a Polyhedron?
    3. POLYHEDRA, GRAPHS AND SURFACES 3.1. From Polyhedra to Graphs What is a Polyhedron? Now that we’ve covered lots of geometry in two dimensions, let’s make things just a little more difficult. We’re going to consider geometric objects in three dimensions which can be made from two-dimensional pieces. For example, you can take six squares all the same size and glue them together to produce the shape which we call a cube. More generally, if you take a bunch of polygons and glue them together so that no side gets left unglued, then the resulting object is usually called a polyhedron.1 The corners of the polygons are called vertices, the sides of the polygons are called edges and the polygons themselves are called faces. So, for example, the cube has 8 vertices, 12 edges and 6 faces. Different people seem to define polyhedra in very slightly different ways. For our purposes, we will need to add one little extra condition — that the volume bound by a polyhedron “has no holes”. For example, consider the shape obtained by drilling a square hole straight through the centre of a cube. Even though the surface of such a shape can be constructed by gluing together polygons, we don’t consider this shape to be a polyhedron, because of the hole. We say that a polyhedron is convex if, for each plane which lies along a face, the polyhedron lies on one side of that plane. So, for example, the cube is a convex polyhedron while the more complicated spec- imen of a polyhedron pictured on the right is certainly not convex.
    [Show full text]