Multiple Data Sources and Integrated Hydrological Modelling for Groundwater Assessment in the Central Kalahari Basin
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Land Tenure Reforms and Social Transformation in Botswana: Implications for Urbanization
Land Tenure Reforms and Social Transformation in Botswana: Implications for Urbanization. Item Type text; Electronic Dissertation Authors Ijagbemi, Bayo, 1963- Publisher The University of Arizona. Rights Copyright © is held by the author. Digital access to this material is made possible by the University Libraries, University of Arizona. Further transmission, reproduction or presentation (such as public display or performance) of protected items is prohibited except with permission of the author. Download date 06/10/2021 17:13:55 Link to Item http://hdl.handle.net/10150/196133 LAND TENURE REFORMS AND SOCIAL TRANSFORMATION IN BOTSWANA: IMPLICATIONS FOR URBANIZATION by Bayo Ijagbemi ____________________ Copyright © Bayo Ijagbemi 2006 A Dissertation Submitted to the Faculty of the DEPARTMENT OF ANTHROPOLOGY In Partial Fulfillment of the Requirements For the Degree of DOCTOR OF PHILOSOPHY In the Graduate College THE UNIVERSITY OF ARIZONA 2006 2 THE UNIVERSITY OF ARIZONA GRADUATE COLLEGE As members of the Dissertation Committee, we certify that we have read the dissertation prepared by Bayo Ijagbemi entitled “Land Reforms and Social Transformation in Botswana: Implications for Urbanization” and recommend that it be accepted as fulfilling the dissertation requirement for the Degree of Doctor of Philosophy _______________________________________________________________________ Date: 10 November 2006 Dr Thomas Park _______________________________________________________________________ Date: 10 November 2006 Dr Stephen Lansing _______________________________________________________________________ Date: 10 November 2006 Dr David Killick _______________________________________________________________________ Date: 10 November 2006 Dr Mamadou Baro Final approval and acceptance of this dissertation is contingent upon the candidate’s submission of the final copies of the dissertation to the Graduate College. I hereby certify that I have read this dissertation prepared under my direction and recommend that it be accepted as fulfilling the dissertation requirement. -

Botswana Semiology Research Centre Project Seismic Stations In
BOTSWANA SEISMOLOGICAL NETWORK ( BSN) STATIONS 19°0'0"E 20°0'0"E 21°0'0"E 22°0'0"E 23°0'0"E 24°0'0"E 25°0'0"E 26°0'0"E 27°0'0"E 28°0'0"E 29°0'0"E 30°0'0"E 1 S 7 " ° 0 0 ' ' 0 0 ° " 7 S 1 KSANE Kasane ! !Kazungula Kasane Forest ReserveLeshomo 1 S Ngoma Bridge ! 8 " ! ° 0 0 ' # !Mabele * . MasuzweSatau ! ! ' 0 ! ! Litaba 0 ° Liamb!ezi Xamshiko Musukub!ili Ivuvwe " 8 ! ! ! !Seriba Kasane Forest Reserve Extension S 1 !Shishikola Siabisso ! ! Ka!taba Safari Camp ! Kachikau ! ! ! ! ! ! Chobe Forest Reserve ! !! ! Karee ! ! ! ! ! Safari Camp Dibejam!a ! ! !! ! ! ! ! X!!AUD! M Kazuma Forest Reserve ! ShongoshongoDugamchaRwelyeHau!xa Marunga Xhauga Safari Camp ! !SLIND Chobe National Park ! Kudixama Diniva Xumoxu Xanekwa Savute ! Mah!orameno! ! ! ! Safari Camp ! Maikaelelo Foreset Reserve Do!betsha ! ! Dibebe Tjiponga Ncamaser!e Hamandozi ! Quecha ! Duma BTLPN ! #Kwiima XanekobaSepupa Khw!a CHOBE DISTRICT *! !! ! Manga !! Mampi ! ! ! Kangara # ! * Gunitsuga!Njova Wazemi ! ! G!unitsuga ! Wazemi !Seronga! !Kaborothoa ! 1 S Sibuyu Forest Reserve 9 " Njou # ° 0 * ! 0 ' !Nxaunxau Esha 12 ' 0 Zara ! ! 0 ° ! ! ! " 9 ! S 1 ! Mababe Quru!be ! ! Esha 1GMARE Xorotsaa ! Gumare ! ! Thale CheracherahaQNGWA ! ! GcangwaKaruwe Danega ! ! Gqose ! DobeQabi *# ! ! ! ! Bate !Mahito Qubi !Mahopa ! Nokaneng # ! Mochabana Shukumukwa * ! ! Nxabe NGAMILAND DISTRICT Sorob!e ! XurueeHabu Sakapane Nxai National Nark !! ! Sepako Caecae 2 ! ! S 0 " Konde Ncwima ° 0 ! MAUN 0 ' ! ! ' 0 Ntabi Tshokatshaa ! 0 ° ! " 0 PHDHD Maposa Mmanxotai S Kaore ! ! Maitengwe 2 ! Tsau Segoro -

E-Government and Democracy in Botswana: Observational and Experimental Evidence on the Effects of E-Government Usage on Political Attitudes
A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Bante, Jana et al. Working Paper E-government and democracy in Botswana: Observational and experimental evidence on the effects of e-government usage on political attitudes Discussion Paper, No. 16/2021 Provided in Cooperation with: German Development Institute / Deutsches Institut für Entwicklungspolitik (DIE), Bonn Suggested Citation: Bante, Jana et al. (2021) : E-government and democracy in Botswana: Observational and experimental evidence on the effects of e-government usage on political attitudes, Discussion Paper, No. 16/2021, ISBN 978-3-96021-153-2, Deutsches Institut für Entwicklungspolitik (DIE), Bonn, http://dx.doi.org/10.23661/dp16.2021 This Version is available at: http://hdl.handle.net/10419/234177 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur Verfügung gestellt haben sollten, If the documents have been made available under an Open gelten abweichend von diesen Nutzungsbedingungen die in der dort Content Licence (especially Creative Commons Licences), you genannten Lizenz gewährten Nutzungsrechte. -
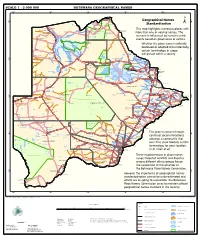
Geographical Names Standardization BOTSWANA GEOGRAPHICAL
SCALE 1 : 2 000 000 BOTSWANA GEOGRAPHICAL NAMES 20°0'0"E 22°0'0"E 24°0'0"E 26°0'0"E 28°0'0"E Kasane e ! ob Ch S Ngoma Bridge S " ! " 0 0 ' ' 0 0 ° Geographical Names ° ! 8 !( 8 1 ! 1 Parakarungu/ Kavimba ti Mbalakalungu ! ± n !( a Kakulwane Pan y K n Ga-Sekao/Kachikaubwe/Kachikabwe Standardization w e a L i/ n d d n o a y ba ! in m Shakawe Ngarange L ! zu ! !(Ghoha/Gcoha Gate we !(! Ng Samochema/Samochima Mpandamatenga/ This map highlights numerous places with Savute/Savuti Chobe National Park !(! Pandamatenga O Gudigwa te ! ! k Savu !( !( a ! v Nxamasere/Ncamasere a n a CHOBE DISTRICT more than one or varying names. The g Zweizwe Pan o an uiq !(! ag ! Sepupa/Sepopa Seronga M ! Savute Marsh Tsodilo !(! Gonutsuga/Gonitsuga scenario is influenced by human-centric Xau dum Nxauxau/Nxaunxau !(! ! Etsha 13 Jao! events based on governance or culture. achira Moan i e a h hw a k K g o n B Cakanaca/Xakanaka Mababe Ta ! u o N r o Moremi Wildlife Reserve Whether the place name is officially X a u ! G Gumare o d o l u OKAVANGO DELTA m m o e ! ti g Sankuyo o bestowed or adopted circumstantially, Qangwa g ! o !(! M Xaxaba/Cacaba B certain terminology in usage Nokaneng ! o r o Nxai National ! e Park n Shorobe a e k n will prevail within a society a Xaxa/Caecae/Xaixai m l e ! C u a n !( a d m a e a a b S c b K h i S " a " e a u T z 0 d ih n D 0 ' u ' m w NGAMILAND DISTRICT y ! Nxai Pan 0 m Tsokotshaa/Tsokatshaa 0 Gcwihabadu C T e Maun ° r ° h e ! 0 0 Ghwihaba/ ! a !( o 2 !( i ata Mmanxotae/Manxotae 2 g Botet N ! Gcwihaba e !( ! Nxharaga/Nxaraga !(! Maitengwe -

Botswana. Supervisor of Elections. . Report to the Minister of State on the General Elections, 1974
Botswana. Supervisor of Elections. Report to the Minister of State on the general elections, 1974. Gaborone, Government Printer [1974?] / 30p. 29cm. 1. Botswana-Pol. & govt. 2. Elections- Botswana. I • INDEX Page. Report to the Minister of State on the General Elections, 1974 Evaluation and Recommendations *"* Conclusion ...... 2 - • • • • 4 Title Appendix lA' A list of Constituencies, Polling Districts and Polling Stations showing the number of registered voters by constituency and polling station Appendix '/?' Authenticating Officers appointed in accordance with the Presidential Elections (Supplementary Provisions) Act >;• 12 Appendix 'C A list of Returning Officers for the Parliamentary Elections • ! l 13 Appendix Z)' A list of Returning Officers for the Local Government Elections .. ^ . 14 Appendix 'ZT Summary of the Parliamentary election results Appendix lF 17 A list of candidates in the Parliamentary Election showing the number of votes cast for each, number of votes in each constituency, and the majority gained by the winning can- didate and the percentage poll 18 Appendix '6" Summary of Local Government Election results by District or Town Council 20 Appendix 'IT A list of candidates in the Local Government election showing the number of votes cast tor each, the number of voters in each Polling District, the majority gained by the win- ning candidate, and the percentage poll / 22 Appendix T A list of political Parries registered under Section 149 of the Electoral Act 1969 30 Appendix ' J" A Report on-expenditure on the 1974 General Election 30 Sir, REPORT TO ™E MINISTER. OF STATE ON THE GENERAL ELECTIONS, 1974 SSSITOSSS: S.»=^^HS£s~rr?' Lo^l Government Election* become generally available to the public - - - > »S5S^S^as: • l^^sstsss^aSSSS^5^^-^-"5 5. -

Establishment of Subordinate Land Boards (Amendment) Order
CHAPTER 32:02 - TRIBAL LAND: SUBSIDIARY LEGISLATION INDEX TO SUBSIDIARY LEGISLATION Establishment of Subordinate Land Boards (Amendment) Order Establishment of Subordinate Land Boards Order Tribal Land (Establishment of Land Tribunals) Order Tribal Land (Subordinate Land Boards) Regulations Tribal Land Regulations ESTABLISHMENT OF SUBORDINATE LAND BOARDS ORDER (under section 19) (15th June, 1973) ARRANGEMENT OF PARAGRAPHS PARAGRAPH 1. Citation 2. Establishment 3. Area of jurisdiction 4. Functions Schedule S.I. 47, 1973, S.I. 3, 1979, S.I. 125, 1979, S.I. 132, 1980, S.I. 78, 1981, S.I. 81, 1981, S.I. 110, 1981, S.I. 68, 1982, S.I. 5, 1984, S.I. 92, 1984, S.I. 36, 1986, S.I. 55,1987, S.I. 97, 1989, S.I. 45, 1992, S.I. 66, 1994, S.I. 53, 2002. 1. Citation Copyright Government of Botswana This Order may be cited as the Establishment of Subordinate Land Boards Order. 2. Establishment The subordinate land boards referred to in the second column of the Schedule hereto are established as the subordinate land boards within the district named in the first column of the said Schedule. 3. Area of jurisdiction The area of jurisdiction in respect of which each subordinate Land Board will perform its functions shall be the area or villages stated in relation to each subordinate land board in the third column of the Schedule. 4. Functions (1) The functions under customary law which vest in the subordinate land authority which are transferred to the subordinate land board shall include the hearing, grant or refusal of applications to use land for— ( a) building residences or extensions thereto; ( b) ploughing to a maximum extent of land determined by the tribal land board; ( c) grazing cattle or other stock; ( d) communal uses in the village. -
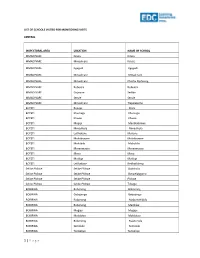
List of Schools Visited for Monitoring Visits
LIST OF SCHOOLS VISITED FOR MONITORING VISITS CENTRAL INSPECTORAL AREA LOCATION NAME OF SCHOOL MMADINARE Diloro Diloro MMADINARE Mmadinare Kelele MMADINARE Kgagodi Kgagodi MMADINARE Mmadinare Mmadinare MMADINARE Mmadinare Phethu Mphoeng MMADINARE Robelela Robelela MMADINARE Gojwane Sedibe MMADINARE Serule Serule MMADINARE Mmadinare Tlapalakoma BOTETI Rakops Etsile BOTETI Khumaga Khumaga BOTETI Khwee Khwee BOTETI Mopipi Manthabakwe BOTETI Mmadikola Mmadikola BOTETI Letlhakane Mokane BOTETI Mokoboxane Mokoboxane BOTETI Mokubilo Mokubilo BOTETI Moreomaoto Moreomaoto BOTETI Mosu Mosu BOTETI Motlopi Motlopi BOTETI Letlhakane Retlhatloleng Selibe Phikwe Selibe Phikwe Boitshoko Selibe Phikwe Selibe Phikwe Boswelakgomo Selibe Phikwe Selibe Phikwe Phikwe Selibe Phikwe Selibe Phikwe Tebogo BOBIRWA Bobonong Bobonong BOBIRWA Gobojango Gobojango BOBIRWA Bobonong Mabumahibidu BOBIRWA Bobonong Madikwe BOBIRWA Mogapi Mogapi BOBIRWA Molalatau Molalatau BOBIRWA Bobonong Rasetimela BOBIRWA Semolale Semolale BOBIRWA Tsetsebye Tsetsebye 1 | P a g e MAHALAPYE WEST Bonwapitse Bonwapitse MAHALAPYE WEST Mahalapye Leetile MAHALAPYE WEST Mokgenene Mokgenene MAHALAPYE WEST Moralane Moralane MAHALAPYE WEST Mosolotshane Mosolotshane MAHALAPYE WEST Otse Setlhamo MAHALAPYE WEST Mahalapye St James MAHALAPYE WEST Mahalapye Tshikinyega MHALAPYE EAST Mahalapye Flowertown MHALAPYE EAST Mahalapye Mahalapye MHALAPYE EAST Matlhako Matlhako MHALAPYE EAST Mmaphashalala Mmaphashalala MHALAPYE EAST Sefhare Mmutle PALAPYE NORTH Goo-Sekgweng Goo-Sekgweng PALAPYE NORTH Goo-Tau Goo-Tau -

National Broadband Strategy
MINISTRY OF TRANSPORT AND COMMUNICATIONS NATIONAL BROADBAND STRATEGY June 2018 Table of Contents LIST OF FIGURES .................................................................................................................... 4 LIST OF TABLES ...................................................................................................................... 5 ABBREVIATIONS .................................................................................................................... 6 EXECUTIVE SUMMARY ........................................................................................................... 7 1 INTRODUCTION .............................................................................................................. 9 2 SITUATIONAL ANALYSIS ............................................................................................... 11 2.1 International Connectivity ................................................................................................................................. 11 2.2 National Backbone ................................................................................................................................................ 11 2.3 Backhauling .............................................................................................................................................................. 11 2.4 Mobile Coverage .................................................................................................................................................... -
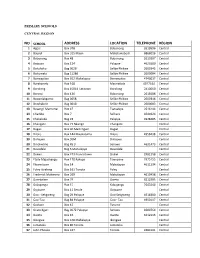
Public Primary Schools
PRIMARY SCHOOLS CENTRAL REGION NO SCHOOL ADDRESS LOCATION TELE PHONE REGION 1 Agosi Box 378 Bobonong 2619596 Central 2 Baipidi Box 315 Maun Makalamabedi 6868016 Central 3 Bobonong Box 48 Bobonong 2619207 Central 4 Boipuso Box 124 Palapye 4620280 Central 5 Boitshoko Bag 002B Selibe Phikwe 2600345 Central 6 Boitumelo Bag 11286 Selibe Phikwe 2600004 Central 7 Bonwapitse Box 912 Mahalapye Bonwapitse 4740037 Central 8 Borakanelo Box 168 Maunatlala 4917344 Central 9 Borolong Box 10014 Tatitown Borolong 2410060 Central 10 Borotsi Box 136 Bobonong 2619208 Central 11 Boswelakgomo Bag 0058 Selibe Phikwe 2600346 Central 12 Botshabelo Bag 001B Selibe Phikwe 2600003 Central 13 Busang I Memorial Box 47 Tsetsebye 2616144 Central 14 Chadibe Box 7 Sefhare 4640224 Central 15 Chakaloba Bag 23 Palapye 4928405 Central 16 Changate Box 77 Nkange Changate Central 17 Dagwi Box 30 Maitengwe Dagwi Central 18 Diloro Box 144 Maokatumo Diloro 4958438 Central 19 Dimajwe Box 30M Dimajwe Central 20 Dinokwane Bag RS 3 Serowe 4631473 Central 21 Dovedale Bag 5 Mahalapye Dovedale Central 22 Dukwi Box 473 Francistown Dukwi 2981258 Central 23 Etsile Majashango Box 170 Rakops Tsienyane 2975155 Central 24 Flowertown Box 14 Mahalapye 4611234 Central 25 Foley Itireleng Box 161 Tonota Foley Central 26 Frederick Maherero Box 269 Mahalapye 4610438 Central 27 Gasebalwe Box 79 Gweta 6212385 Central 28 Gobojango Box 15 Kobojango 2645346 Central 29 Gojwane Box 11 Serule Gojwane Central 30 Goo - Sekgweng Bag 29 Palapye Goo-Sekgweng 4918380 Central 31 Goo-Tau Bag 84 Palapye Goo - Tau 4950117 -

Impact of Maternal Effects on Ranking of Animal Models for Genetic
Scientific Journal of Zoology (2013) 2(4) 36-39 ISSN 2322-293X Contents lists available at Sjournals Journal homepage: www.Sjournals.com Original article Ethnozoological survey of traditional medicinal uses of tortoises in Lentsweletau and Botlhapatlou villages in Kweneng district of Botswana M.R. Setlalekgomo* Botswana College of Agriculture, Department of Basic Sciences, Private Bag 0027, Gaborone, Botswana. * Corresponding author; Botswana College of Agriculture, Department of Basic Sciences, Private Bag 0027, Gaborone, Botswana. A R T I C L E I N F O A B S T R A C T Article history: A study was carried out to document the traditional medicinal uses Received 03 April 2013 of tortoises at Ramankhung, Lekgalung and Dikateng fields near Accepted 14 April 2013 Lentsweletau village and at Mmaphoroka and Moleleme fields near Available online 25 April 2013 Botlhapatlou village in Kweneng district of Botswana. A formal questionnaire was administered to 47 respondents (nearly 10 Keywords: respondents per study site). The respondents were 46.81% farmers, Carapace 36.17% cattle herders, 14.89% farm labourers and 2.13% Ethnozoology unemployed. The study showed that different parts of tortoises are Plastron used in traditional medicine to treat various human ailments in Traditional medicine Lentsweletau and Botlhapatlou villages in Kweneng district of Tortoise Botswana. Uses © 2013 Sjournals. All rights reserved. 1. Introduction Animals are vital to man’s existence in that they provide him with various materials such as food, clothes, transport and others (Jaroli et al., 2010). Some animals are known to have medicinal value and to be used by man in traditional medicine (Kim and Song, 2013). -

Geological Survey Department
REPUBLIC OF BOTSWANA ;". ANNUAL REPORT OFTHE GEOLOGICAL SURVEY DEPARTMENT FOR THE YEAR 199J-; PRICE: P3,OO Printed by the Government Printer, Gaborone Botswana GEOLOGICAL SURVEY DEPARTMENT (Director: T. P. Machacha) ANNUAL REPORT OF THE GEOLOGICAL SURVEY DEPARTMENT FOR THE YEAR 1992 PUblished by The Director Geological Survey Department Private Bag 14, Lobatse, Botswana. With the authority of The Ministry of Mineral Resources and Water Affairs Republic of Botswana 1. GENERAL The Geological Survey remained within the Ministry of Mineral Resources and Water Affairs and continued with its main functions of gathering, assessing and disseminating all data related to the rocks, mineral deposits and grouhdwater resources of Botswana. The departmental organisational structure continued to consist of the Directorate, four operational divisions of Regional Geology, Economic Geology, Hydrogeology and Geophysics together with an Administrative Division. Support to the main divisions was provided by the Drawing Office, Technical Records and Library, Chemistry and Mineral Dressing Laboratories. During the year the staffing position within the Department was consolidated with a full establishment of professional staff. There were no changes in the Directorate although the Deputy Director spent much of the year in Canada completing his PhD studies. The Principal Regional Geologist, Mr D P Piper, returned to the U K in July and was replaced by Dr R M Key who arrived from the U K in October. Within the Economic Division the evaluation of industrial minerals continued to be given priority with extensive investigations in the Dukwe-Matsitama, Selibe-Phikwe and Palapye areas. The writing of the gold monograph continued, as did the exploration for base and precious metals in the Maitengwe Schist Belt. -

Botswana & Namibia
0 200 km Botswana & Namibia 0 120 miles ZAMBIA Skeleton Coast Etosha National Park Victoria Falls ANGOLA Cubango Tsodilo Hills Steeped in myth and Watching wildlife doesn't Katima Mpalila Zambezi The mightiest waterfall Ruacana Ancient San Mulilo NP mist get easier ANGOLA Imusho Island Lakeon eaKaribarth Falls rock art Calueque Katwitwi Kasane Otjinungwa Oshikango River Calai Mudumu Chobe Livingstone ZIMBABWE Skelet Ruacana Nkurenkuru Andara NP River Victoria Falls Okongwati Oshakati CAPRIVI STRIP Linyanti Kasane Ehomba Bwabwata NP Chobe FR Zambezi (1868m) Ondangwa OWAMBO Rundu Mahango GR FR River on Ongandjera REGION Shakawe Mamili NP Kazuma KAOKOVELD Opuwo Lake KAVANGO Tsodilo 18ºS Coast Savuti FR Pandamatenga Chobe National Park Schwarze Kuppen Oponono REGION Hills An astounding array Mangetti Chobe NP Cabo Fria (1869m) Etosha Khaudum Xaa Moremi Wilderness Karakuwisa Etsha 6 Sibuyu of wildlife Pan NP Nxaunxau GR FR Purros Etosha Tsumeb Kudumane Kano Gumare Sesfontein NP Maroelaboom Tsumkwe Okavango Moremi Game Reserve Rocky Point Vlei Delta Nxai Botswana’s wildlife Nokaneng Shorobe Pan River River Kamanjab Otavi Grootfontein Nxai Pan NP central DAMARALAND Aha Hills Konde Hoanib OTJOZONDJUPA Maun Matlapaneng Gweta Palmwag (1250m) Gcwihaba Nata Nata Bulawayo Omatako River (Drotsky's) Cave Toteng Sanctuary Semowane Terrace Bay River Outjo Waterberg Petrified Plateau Park Sehithwa Tutume Otjosondjou Makgadikgadi Ntwetwe Plumtree 20ºS Torra Bay Uniab Forest Khorixas Pans NP Masunga Otjiwarongo Okakarara River Pan Siviya Twyfelfontein Sowa