9 Molecular Orbitals in Chemical Bonding
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The Dependence of the Sio Bond Length on Structural Parameters in Coesite, the Silica Polymorphs, and the Clathrasils
American Mineralogist, Volume 75, pages 748-754, 1990 The dependence of the SiO bond length on structural parameters in coesite, the silica polymorphs, and the clathrasils M. B. BOISEN, JR. Department of Mathematics, Virginia Polytechnic Institute and State University, Blacksburg, Virginia 24061, U.S.A. G. V. GIBBS, R. T. DOWNS Department of Geological Sciences, Virginia Polytechnic Institute and State University, Blacksburg, Virginia 24061, U.S.A. PHILIPPE D' ARCO Laboratoire de Geologie, Ecole Normale Superieure, 75230 Paris Cedex OS, France ABSTRACT Stepwise multiple regression analyses of the apparent R(SiO) bond lengths were com- pleted for coesite and for the silica polymorphs together with the clathrasils as a function of the variables};(O), P (pressure), f,(Si), B(O), and B(Si). The analysis of 94 bond-length data recorded for coesite at a variety of pressures and temperatures indicates that all five of these variables make a significant contribution to the regression sum of squares with an R2 value of 0.84. A similar analysis of 245 R(SiO) data recorded for silica polymorphs and clathrasils indicate that only three of the variables (B(O), };(O), and P) make a signif- icant contribution to the regression with an R2 value of 0.90. The distribution of B(O) shows a wide range of values from 0.25 to 10.0 A2 with nearly 80% of the observations clustered between 0.25 and 3.0 A2 and the remaining values spread uniformly between 4.5 and 10.0 A2. A regression analysis carried out for these two populations separately indicates, for the data set with B(O) values less than three, that };(O) B(O), P, and };(Si) are all significant with an R2 value of 0.62. -

Chemistry 2000 Slide Set 1: Introduction to the Molecular Orbital Theory
Chemistry 2000 Slide Set 1: Introduction to the molecular orbital theory Marc R. Roussel January 2, 2020 Marc R. Roussel Introduction to molecular orbitals January 2, 2020 1 / 24 Review: quantum mechanics of atoms Review: quantum mechanics of atoms Hydrogenic atoms The hydrogenic atom (one nucleus, one electron) is exactly solvable. The solutions of this problem are called atomic orbitals. The square of the orbital wavefunction gives a probability density for the electron, i.e. the probability per unit volume of finding the electron near a particular point in space. Marc R. Roussel Introduction to molecular orbitals January 2, 2020 2 / 24 Review: quantum mechanics of atoms Review: quantum mechanics of atoms Hydrogenic atoms (continued) Orbital shapes: 1s 2p 3dx2−y 2 3dz2 Marc R. Roussel Introduction to molecular orbitals January 2, 2020 3 / 24 Review: quantum mechanics of atoms Review: quantum mechanics of atoms Multielectron atoms Consider He, the simplest multielectron atom: Electron-electron repulsion makes it impossible to solve for the electronic wavefunctions exactly. A fourth quantum number, ms , which is associated with a new type of angular momentum called spin, enters into the theory. 1 1 For electrons, ms = 2 or − 2 . Pauli exclusion principle: No two electrons can have identical sets of quantum numbers. Consequence: Only two electrons can occupy an orbital. Marc R. Roussel Introduction to molecular orbitals January 2, 2020 4 / 24 The hydrogen molecular ion The quantum mechanics of molecules + H2 is the simplest possible molecule: two nuclei one electron Three-body problem: no exact solutions However, the nuclei are more than 1800 time heavier than the electron, so the electron moves much faster than the nuclei. -

Theoretical Methods That Help Understanding the Structure and Reactivity of Gas Phase Ions
International Journal of Mass Spectrometry 240 (2005) 37–99 Review Theoretical methods that help understanding the structure and reactivity of gas phase ions J.M. Merceroa, J.M. Matxaina, X. Lopeza, D.M. Yorkb, A. Largoc, L.A. Erikssond,e, J.M. Ugaldea,∗ a Kimika Fakultatea, Euskal Herriko Unibertsitatea, P.K. 1072, 20080 Donostia, Euskadi, Spain b Department of Chemistry, University of Minnesota, 207 Pleasant St. SE, Minneapolis, MN 55455-0431, USA c Departamento de Qu´ımica-F´ısica, Universidad de Valladolid, Prado de la Magdalena, 47005 Valladolid, Spain d Department of Cell and Molecular Biology, Box 596, Uppsala University, 751 24 Uppsala, Sweden e Department of Natural Sciences, Orebro¨ University, 701 82 Orebro,¨ Sweden Received 27 May 2004; accepted 14 September 2004 Available online 25 November 2004 Abstract The methods of the quantum electronic structure theory are reviewed and their implementation for the gas phase chemistry emphasized. Ab initio molecular orbital theory, density functional theory, quantum Monte Carlo theory and the methods to calculate the rate of complex chemical reactions in the gas phase are considered. Relativistic effects, other than the spin–orbit coupling effects, have not been considered. Rather than write down the main equations without further comments on how they were obtained, we provide the reader with essentials of the background on which the theory has been developed and the equations derived. We committed ourselves to place equations in their own proper perspective, so that the reader can appreciate more profoundly the subtleties of the theory underlying the equations themselves. Finally, a number of examples that illustrate the application of the theory are presented and discussed. -

The Nafure of Silicon-Oxygen Bonds
AmericanMineralogist, Volume 65, pages 321-323, 1980 The nafure of silicon-oxygenbonds LtNus PeurrNc Linus Pauling Institute of Scienceand Medicine 2700 Sand Hill Road, Menlo Park, California 94025 Abstract Donnay and Donnay (1978)have statedthat an electron-densitydetermination carried out on low-quartz by R. F. Stewart(personal communication), which assignscharges -0.5 to the oxygen atoms and +1.0 to the silicon atoms, showsthe silicon-oxygenbond to be only 25 percentionic, and hencethat "the 50/50 descriptionofthe past fifty years,which was based on the electronegativity difference between Si and O, is incorrect." This conclusion, however, ignoresthe evidencethat each silicon-oxygenbond has about 55 percentdouble-bond char- acter,the covalenceof silicon being 6.2,with transferof 2.2 valenc,eelectrons from oxygen to silicon. Stewart'svalue of charge*1.0 on silicon then leads to 52 percentionic characterof the bonds, in excellentagreement with the value 5l percent given by the electronegativity scale. Donnay and Donnay (1978)have recently referred each of the four surrounding oxygen atoms,this ob- to an "absolute" electron-densitydetermination car- servationleads to the conclusionthat the amount of ried out on low-quartz by R. F. Stewart, and have ionic character in the silicon-oxygsa 5ingle bond is statedthat "[t showsthe Si-O bond to be 75 percent 25 percent. It is, however,not justified to make this covalent and only 25 percent ionic; the 50/50 de- assumption. scription of the past fifty years,which was basedon In the first edition of my book (1939)I pointed out the electronegativitydifference between Si and O, is that the observedSi-O bond length in silicates,given incorrect." as 1.604, is about 0.20A less than the sum of the I formulated the electronegativityscale in 1932, single-bond radii of the two atoms (p. -
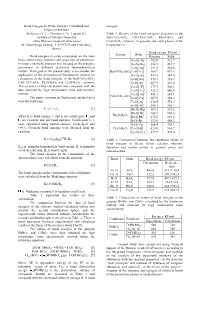
Bond Energies in Oxide Systems: Calculated and Experimental Data
Bond Energies In Oxide Systems: Calculated and energies. Experimental Data Stolyarova V. L., Plotnikov E.N., Lopatin S.I. Table 1. Results of the bond energies calculation in the Institute of Silicate Chemistry BaO-TiO 2-SiO 2, CaO-TiO 2-SiO 2, Rb 2O-B2O3 and of the Russian Academy of Sciences Cs 2O-B2O3 systems. in gaseous and solid phases at the ul. Odoevskogo 24 korp. 2, 199155 Sankt Petersburg, temperature 0 ¥ . Russia Bond energy, KJ/mol System Bond Bond energies in oxide compounds are the main Gaseous Solid factor determining structure and properties of substances. Ba-O[-Ti] 382.0 512.7 In some cases bond energies may be used as the energetic Ba-O[-Ba] 348.5 467.7 parameters in different statistical thermodynamical Ti-O[-Ba] 331.8 450.6 models. Main goal of the present study is to consider the BaO-TiO 2-SiO 2 Ti-O[-Ti] 364.7 497.6 application of the semiempirical Sanderson's method for Ba-O[-Si] 437.6 585.4 calculation of the bond energies in the BaO-TiO 2-SiO 2, Si-O[-Ba] 270.3 334.7 CaO-TiO 2-SiO 2, Rb 2O-B2O3 and Cs 2O-B2O3 systems. Si-O[-Si] 407.9 421.0 The accuracy of this calculation was compared with the Ca-O[-Ti] 377.1 500.1 data obtained by high temperature mass spectrometric Ca-O[-Ca] 322.2 486.8 method. Ca-O[-Si] 441.1 585.1 CaO-TiO -SiO The main equations in Sanderson's method used 2 2 Si-O[-Ca] 287.9 358.2 were the following. -

Molecular Orbital Theory to Predict Bond Order • to Apply Molecular Orbital Theory to the Diatomic Homonuclear Molecule from the Elements in the Second Period
Skills to Develop • To use molecular orbital theory to predict bond order • To apply Molecular Orbital Theory to the diatomic homonuclear molecule from the elements in the second period. None of the approaches we have described so far can adequately explain why some compounds are colored and others are not, why some substances with unpaired electrons are stable, and why others are effective semiconductors. These approaches also cannot describe the nature of resonance. Such limitations led to the development of a new approach to bonding in which electrons are not viewed as being localized between the nuclei of bonded atoms but are instead delocalized throughout the entire molecule. Just as with the valence bond theory, the approach we are about to discuss is based on a quantum mechanical model. Previously, we described the electrons in isolated atoms as having certain spatial distributions, called orbitals, each with a particular orbital energy. Just as the positions and energies of electrons in atoms can be described in terms of atomic orbitals (AOs), the positions and energies of electrons in molecules can be described in terms of molecular orbitals (MOs) A particular spatial distribution of electrons in a molecule that is associated with a particular orbital energy.—a spatial distribution of electrons in a molecule that is associated with a particular orbital energy. As the name suggests, molecular orbitals are not localized on a single atom but extend over the entire molecule. Consequently, the molecular orbital approach, called molecular orbital theory is a delocalized approach to bonding. Although the molecular orbital theory is computationally demanding, the principles on which it is based are similar to those we used to determine electron configurations for atoms. -

Introduction to Molecular Orbital Theory
Chapter 2: Molecular Structure and Bonding Bonding Theories 1. VSEPR Theory 2. Valence Bond theory (with hybridization) 3. Molecular Orbital Theory ( with molecualr orbitals) To date, we have looked at three different theories of molecular boning. They are the VSEPR Theory (with Lewis Dot Structures), the Valence Bond theory (with hybridization) and Molecular Orbital Theory. A good theory should predict physical and chemical properties of the molecule such as shape, bond energy, bond length, and bond angles.Because arguments based on atomic orbitals focus on the bonds formed between valence electrons on an atom, they are often said to involve a valence-bond theory. The valence-bond model can't adequately explain the fact that some molecules contains two equivalent bonds with a bond order between that of a single bond and a double bond. The best it can do is suggest that these molecules are mixtures, or hybrids, of the two Lewis structures that can be written for these molecules. This problem, and many others, can be overcome by using a more sophisticated model of bonding based on molecular orbitals. Molecular orbital theory is more powerful than valence-bond theory because the orbitals reflect the geometry of the molecule to which they are applied. But this power carries a significant cost in terms of the ease with which the model can be visualized. One model does not describe all the properties of molecular bonds. Each model desribes a set of properties better than the others. The final test for any theory is experimental data. Introduction to Molecular Orbital Theory The Molecular Orbital Theory does a good job of predicting elctronic spectra and paramagnetism, when VSEPR and the V-B Theories don't. -

8.3 Bonding Theories >
8.3 Bonding Theories > Chapter 8 Covalent Bonding 8.1 Molecular Compounds 8.2 The Nature of Covalent Bonding 8.3 Bonding Theories 8.4 Polar Bonds and Molecules 1 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals Molecular Orbitals How are atomic and molecular orbitals related? 2 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals • The model you have been using for covalent bonding assumes the orbitals are those of the individual atoms. • There is a quantum mechanical model of bonding, however, that describes the electrons in molecules using orbitals that exist only for groupings of atoms. 3 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals • When two atoms combine, this model assumes that their atomic orbitals overlap to produce molecular orbitals, or orbitals that apply to the entire molecule. 4 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals Just as an atomic orbital belongs to a particular atom, a molecular orbital belongs to a molecule as a whole. • A molecular orbital that can be occupied by two electrons of a covalent bond is called a bonding orbital. 5 Copyright © Pearson Education, Inc., or its affiliates. All Rights Reserved. 8.3 Bonding Theories > Molecular Orbitals Sigma Bonds When two atomic orbitals combine to form a molecular orbital that is symmetrical around the axis connecting two atomic nuclei, a sigma bond is formed. • Its symbol is the Greek letter sigma (σ). -

Atomic Structures of the M Olecular Components in DNA and RNA Based on Bond Lengths As Sums of Atomic Radii
1 Atomic St ructures of the M olecular Components in DNA and RNA based on Bond L engths as Sums of Atomic Radii Raji Heyrovská (Institute of Biophysics, Academy of Sciences of the Czech Republic) E-mail: [email protected] Abstract The author’s interpretation in recent years of bond lengths as sums of the relevant atomic/ionic radii has been extended here to the bonds in the skeletal structures of adenine, guanine, thymine, cytosine, uracil, ribose, deoxyribose and phosphoric acid. On examining the bond length data in the literature, it has been found that the averages of the bond lengths are close to the sums of the corresponding atomic covalent radii of carbon (tetravalent), nitrogen (trivalent), oxygen (divalent), hydrogen (monovalent) and phosphorus (pentavalent). Thus, the conventional molecular structures have been resolved here (for the first time) into probable atomic structures. 1. Introduction The interpretation of the bond lengths in the molecules constituting DNA and RNA have been of interest ever since the discovery [1] of the molecular structure of nucleic acids. This work was motivated by the earlier findings [2a,b] that the inter-atomic distance between any two atoms or ions is, in general, the sum of the radii of the atoms (and or ions) constituting the chemical bond, whether the bond is partially or fully ionic or covalent. It 2 was shown in [3] that the lengths of the hydrogen bonds in the Watson- Crick [1] base pairs (A, T and C, G) of nucleic acids as well as in many other inorganic and biochemical compounds are sums of the ionic or covalent radii of the hydrogen donor and acceptor atoms or ions and of the transient proton involved in the hydrogen bonding. -

Bond Distances and Bond Orders in Binuclear Metal Complexes of the First Row Transition Metals Titanium Through Zinc
Metal-Metal (MM) Bond Distances and Bond Orders in Binuclear Metal Complexes of the First Row Transition Metals Titanium Through Zinc Richard H. Duncan Lyngdoh*,a, Henry F. Schaefer III*,b and R. Bruce King*,b a Department of Chemistry, North-Eastern Hill University, Shillong 793022, India B Centre for Computational Quantum Chemistry, University of Georgia, Athens GA 30602 ABSTRACT: This survey of metal-metal (MM) bond distances in binuclear complexes of the first row 3d-block elements reviews experimental and computational research on a wide range of such systems. The metals surveyed are titanium, vanadium, chromium, manganese, iron, cobalt, nickel, copper, and zinc, representing the only comprehensive presentation of such results to date. Factors impacting MM bond lengths that are discussed here include (a) n+ the formal MM bond order, (b) size of the metal ion present in the bimetallic core (M2) , (c) the metal oxidation state, (d) effects of ligand basicity, coordination mode and number, and (e) steric effects of bulky ligands. Correlations between experimental and computational findings are examined wherever possible, often yielding good agreement for MM bond lengths. The formal bond order provides a key basis for assessing experimental and computationally derived MM bond lengths. The effects of change in the metal upon MM bond length ranges in binuclear complexes suggest trends for single, double, triple, and quadruple MM bonds which are related to the available information on metal atomic radii. It emerges that while specific factors for a limited range of complexes are found to have their expected impact in many cases, the assessment of the net effect of these factors is challenging. -

Covalent Bonding and Molecular Orbitals
Covalent Bonding and Molecular Orbitals Chemistry 35 Fall 2000 From Atoms to Molecules: The Covalent Bond n So, what happens to e- in atomic orbitals when two atoms approach and form a covalent bond? Mathematically: -let’s look at the formation of a hydrogen molecule: -we start with: 1 e-/each in 1s atomic orbitals -we’ll end up with: 2 e- in molecular obital(s) HOW? Make linear combinations of the 1s orbital wavefunctions: ymol = y1s(A) ± y1s(B) Then, solve via the SWE! 2 1 Hydrogen Wavefunctions wavefunctions probability densities 3 Hydrogen Molecular Orbitals anti-bonding bonding 4 2 Hydrogen MO Formation: Internuclear Separation n SWE solved with nuclei at a specific separation distance . How does the energy of the new MO vary with internuclear separation? movie 5 MO Theory: Homonuclear Diatomic Molecules n Let’s look at the s-bonding properties of some homonuclear diatomic molecules: Bond order = ½(bonding e- - anti-bonding e-) For H2: B.O. = 1 - 0 = 1 (single bond) For He2: B.O. = 1 - 1 = 0 (no bond) 6 3 Configurations and Bond Orders: 1st Period Diatomics Species Config. B.O. Energy Length + 1 H2 (s1s) ½ 255 kJ/mol 1.06 Å 2 H2 (s1s) 1 431 kJ/mol 0.74 Å + 2 * 1 He2 (s1s) (s 1s) ½ 251 kJ/mol 1.08 Å 2 * 2 He2 (s1s) (s 1s) 0 ~0 LARGE 7 Combining p-orbitals: s and p MO’s antibonding end-on overlap bonding antibonding side-on overlap bonding antibonding bonding8 4 2nd Period MO Energies s2p has lowest energy due to better overlap (end-on) of 2pz orbitals p2p orbitals are degenerate and at higher energy than the s2p 9 2nd Period MO Energies: Shift! For Z <8: 2s and 2p orbitals can interact enough to change energies of the resulting s2s and s2p MOs. -

3-MO Theory(U).Pptx
Molecular Orbital Theory Valence Bond Theory: Electrons are located in discrete pairs between specific atoms Molecular Orbital Theory: Electrons are located in the molecule, not held in discrete regions between two bonded atoms Thus the main difference between these theories is where the electrons are located, in valence bond theory we predict the electrons are always held between two bonded atoms and in molecular orbital theory the electrons are merely held “somewhere” in molecule Mathematically can represent molecule by a linear combination of atomic orbitals (LCAO) ΨMOL = c1 φ1 + c2 φ2 + c3 φ3 + cn φn Where Ψ2 = spatial distribution of electrons If the ΨMOL can be determined, then where the electrons are located can also be determined 66 Building Molecular Orbitals from Atomic Orbitals Similar to a wave function that can describe the regions of space where electrons reside on time average for an atom, when two (or more) atoms react to form new bonds, the region where the electrons reside in the new molecule are described by a new wave function This new wave function describes molecular orbitals instead of atomic orbitals Mathematically, these new molecular orbitals are simply a combination of the atomic wave functions (e.g LCAO) Hydrogen 1s H-H bonding atomic orbital molecular orbital 67 Building Molecular Orbitals from Atomic Orbitals An important consideration, however, is that the number of wave functions (molecular orbitals) resulting from the mixing process must equal the number of wave functions (atomic orbitals) used in the mixing