DOCSLIB.ORG

A Catalogue of Mathematical Formulas Involving Π, with Analysis

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Catalogue of Mathematical Formulas Involving Π, with Analysis A catalogue of mathematical formulas involving π, with analysis David H. Bailey∗ April 22, 2020 Abstract This paper presents a catalogue of mathematical formulas and iterative algorithms for evaluating the math- ematical constant π, ranging from Archimedes' 2200-year-old iteration to some formulas that were discovered only in the past few decades. Computer implementations and timing results for these formulas and algorithms are also included. In particular, timings are presented for evaluations of various infinite series formulas to approximately 10,000-digit precision, for evaluations of various integral formulas to approximately 4,000-digit precision, and for evaluations of several iterative algorithms to approximately 100,000-digit precision, all based on carefully designed comparative computer runs. 1 Background The mathematical constant known as π = 3:141592653589793 ::: is undeniably the most famous and arguably the most important mathematical constant. Mathematicians since the days of Archimedes, up to and including the present day, have analyzed its properties and computed its numerical value. This paper presents a collection of 72 formulas and algorithms that have been found by mathematicians over the years involving π. While a comprehensive collection is of course not possible, preference is given in this collection for formulas that satisfy the following criteria: • Formulas that give π or a very simple expression involving π explicitly, as opposed to implicit relations such as eiπ + 1 = 0. • Formulas that give π or a very simple expression involving π as an infinite series, definite integral or simple iterative algorithm. • Formulas that involve simple notation, such as summations, integrals, binomial coefficients, exponentials, logarithms, etc., that would be familiar to anyone who has completed a beginning calculus course. • Formulas that are relatively new, discovered within the last 100 years or so. Included in this listing are several formulas for π that have actually have been used in large calculations of π, both before and since the rise of computer technology. These include formulas 2 through 5 prior to the 20th century, and formulas 6, 7, 11, 12, 13, 14, 16, 18, 69 and 71 in the late 20th and early 21st century. Formulas 13 through 18 have the intriguing property that they permit digits (in certain specific bases) of the constant specified on the left-hand side to be calculated beginning at an arbitrary starting position, without needing to calculate any of the digits that came before, by means of relatively simple algorithms. Formulas 13 and 14 have been used in computations of high-order binary digits of π [15, Sec 3.4{3.6], while ∗Lawrence Berkeley National Laboratory, Berkeley, CA 94720 (retired) and University of California, Davis, Department of Com- puter Science, [email protected]. 1 formula 16 has been used in computations of high-order binary digits of π2, and formula 18 has been used in computations of high-order base-3 digits of π2 [11]. Numerous other recently-discovered formulas that possess the arbitrary digit-computation property for various mathematical constants are catalogued in [3]. Many of these formulas are relatively new, in the sense that they were discovered only in the past few decades. The formulas mentioned in the previous paragraph are certainly in this category, having been discovered only since 1996. Many of the formulas from 19 through 50 were not well known until recently. Formulas 64 through 67 are also relatively new, in the sense that they are part of a class of integral formulas that are the subject of current research [8, 9, 10]. Formula 69 was discovered in 1976. Formulas 70, 71 and 72 were first published in 1984. 2 A catalogue of formulas for π 1 π X (−1)n = (1) 4 (2n + 1) n=0 1 1 π X (−1)n X (−1)n = + (2) 4 (2n + 1)22n+1 (2n + 1)32n+1 n=0 n=0 1 1 π X (−1)n X (−1)n = 4 − (3) 4 (2n + 1)52n+1 (2n + 1)2392n+1 n=0 n=0 1 1 1 π X (−1)n X (−1)n X (−1)n = + + (4) 4 (2n + 1)22n+1 (2n + 1)52n+1 (2n + 1)82n+1 n=0 n=0 n=0 1 1 1 π X (−1)n X (−1)n X (−1)n = 3 + + (5) 4 (2n + 1)42n+1 (2n + 1)202n+1 (2n + 1)19852n+1 n=0 n=0 n=0 1 1 1 1 π X (−1)n X (−1)n X (−1)n X (−1)n = 12 + 32 − 5 + 12 4 (2n + 1)492n+1 (2n + 1)572n+1 (2n + 1)2392n+1 (2n + 1)1104432n+1 n=0 n=0 n=0 n=0 (6) 1 1 1 1 π X (−1)n X (−1)n X (−1)n X (−1)n = 44 + 7 − 12 + 24 4 (2n + 1)572n+1 (2n + 1)2392n+1 (2n + 1)6822n+1 (2n + 1)129432n+1 n=0 n=0 n=0 n=0 (7) 1 p X (−1)n π = 12 (8) (2n + 1)3n n=0 p 1 2n 3 3 X π = − 24 n (9) 4 (2n + 3)(2n − 1)42n+1 n=0 1 π Y 4n2 = (10) 2 4n2 − 1 n=1 p 1 1 2 2 X (4n)!(1103 + 26390n) = (11) π 9801 (n!)43964n n=0 1 1 X (−1)n(6n)!(13591409 + 545140134n) = 12 (12) π (3n)!(n!)36403203n+3=2 n=0 2 1 X 1 4 2 1 1 π = − − − (13) 16n 8n + 1 8n + 4 8n + 5 8n + 6 n=0 1 1 X (−1)n 1 X (−1)n 32 8 1 π = 4 − + + (14) 4n(2n + 1) 64 1024n 4n + 1 4n + 2 4n + 3 n=0 n=0 1 X (−1)n 2 2 1 π = + + (15) 4n 4n + 1 4n + 2 4n + 3 n=0 1 2 9 X 1 16 24 8 6 1 π = − − − + (16) 8 64n (6n + 1)2 (6n + 2)2 (6n + 3)2 (6n + 4)2 (6n + 5)2 n=0 1 p 1 X 1 81 54 9 12 3 2 1 π 3 = − − − − − − 9 729n 12n + 1 12n + 2 12n + 4 12n + 6 12n + 7 12n + 8 12n + 10 n=0 (17) 1 2 2 X 1 243 405 81 27 72 π = − − − − 27 729n (12n + 1)2 (12n + 2)2 (12n + 4)2 (12n + 5)2 (12n + 6)2 n=0 9 9 5 1 − − − + (18) (12n + 7)2 (12n + 8)2 (12n + 10)2 (12n + 11)2 1 X 12n22n 3π + 8 = 4n (19) n=0 2n 2 1 2n π 2 X − 2 log 2 = n (20) 6 n24n n=1 1 X (126n2 − 24n + 8)23n 15π + 52 = 6n (21) n=0 3n 1 X (1920n3 − 928n2 + 424n − 16)24n 105π + 304 = 8n (22) n=0 4n 1 p X (49n + 1)8n 16π 3 + 81 = (23) n3n n=0 3 n 1 p X (−245n + 338)8n 162 − 6π 3 − 18 log 3 = (24) n3n n=0 3 n 1 X (50n − 6) π = (25) n3n n=0 2 n 1 X (−4)n(2n)!2(3n)!(201 − 952n) 15π + 42 = (26) (6n)!n! n=1 1 p X 8n(2n)!2(3n)!(350n − 17) 15π 2 + 27 = (27) (6n)!n! n=0 1 p X (−27)n(2n)!2(3n)!(81 − 1080n) 40π 3 + 243 = (28) (6n)!n! n=1 1 p X (−1=3)n(2n)!2(3n)!(4123 − 22100n) 20π 3 + 89 = (29) (6n)!n! n=1 3 1 X (−1=2)n(89012n3 − 77362n2 + 482n + 3028) 15π + 240 log 2 − 528 = 5n (30) n=1 2n 1 p X 9n(2743n2 − 130971n − 12724) 24516 − 360π 3 = 4n (31) n=1 n 1 X 8n(430n2 − 6240n − 520) 45π + 1164 = 4n (32) n=1 n 1 p X 3n(7175n2 − 15215n + 480) 40π 3 + 1872 = 4n (33) n=1 n 1 p X (9=8)n(5692 + 6335n − 5415n2) 288π 3 − 576 log 2 + 324 = 4n (34) n=0 n 1 p X (9=8)n(7517 + 1145n + 18050n2) 1008π 3 − 576 log 2 + 7587 = 4n (35) n=0 n 1 !3 16 X 42n + 5 2n = (36) π 4096n n n=0 1 4 X (−1)n(4n)!(20n + 3) = (37) π 44n(n!)422n+1 n=0 1 4 X (−1)n(4n)!(260n + 23) = (38) π 44n(n!)4182n+1 n=0 1 4 X (−1)n(4n)!(21460n + 1123) = (39) π 44n(n!)48822n+1 n=0 1 2 X (4n)!(8n + 1) p = (40) 44n(n!)432n+1 π 3 n=0 1 1 X (4n)!(10n + 1) p = (41) 44n(n!)492n+1 2π 2 n=0 1 4 X (−1)n(4n)!(28n + 3) p = (42) 44n(n!)43n42n+1 π 3 n=0 1 4 X (−1)n(4n)!(644n + 41) p = (43) 44n(n!)45n722n+1 π 5 n=0 1 1 X (4n)!(40n + 3) p = (44) 44n(n!)4492n+1 3π 3 n=0 1 4n2n4 2 32 X (120n + 34n + 3) = 2n n (45) π2 216n n=0 1 n2n5 2 128 X (−1) (820n + 180n + 13) = n (46) π2 220n n=0 1 !3 2 X n 2n 4n + 1 = (−1) (47) π n 64n n=0 4 1 !3 4 X 2n 6n + 1 = (48) π n 256n n=0 1 X 2n+1 π + 4 = 2n (49) n=0 n 1 6 X (6n)!(532n2 + 126n + 9) = 64 (50) π2 (n!)6106n+3 n=0 π Z 1 dx = 2 (51) 4 0 1 + x π Z 1 p = 1 − x2 dx (52) 4 0 π − 2 Z 1 = x tan−1 x dx (53) 4 0 π(π − 12) log 2 Z 1 + = log x tan−1 x dx (54) 48 2 0 22 Z 1 x4(1 − x)4 dx − π = 2 (55) 7 0 1 + x π Z 1 x2 dx = p (56) 4 4 8 0 (1 + x ) 1 − x π(1 + 2 log 2) Z 1 p = xe−x 1 − e−2x dx (57) 8 0 π3 Z 1 x2 dx 4π log2 2 + = p (58) x 3 0 e − 1 Z π=2 x2 dx π log 2 = 2 (59) 0 sin x π3 π log2 2 Z π=2 + = log2(cos x) dx (60) 24 2 0 8π3 Z 1 log2 x dx p = 2 (61) 81 3 0 x + x + 1 π Z 1 log(1 + x2) dx − log 2 = 2 (62) 2 0 x p Z 1 π = Γ(1=2) = x−1=2e−x dx (63) p0 π 3 log(2 + 3) Z 1 Z 1 Z 1 dx dy dz − + = (64) p 2 2 2 4 2 0 0 0 x + y + z p p π 3 log(2 + 3) Z 1 Z 1 Z 1 p − + + = x2 + y2 + z2 dx dy dz (65) 24 4 2 p p 0 0 0 π 2 3 7 log(2 + 3) Z 1 Z 1 Z 1 − + + = (x2 + y2 + z2)3=2dx dy dz (66) 60 5 20 0 0 0 Z 1 Z 1 x − 1 2 y − 1 2 xy − 1 2 5 − π2 − 4 log 2 + 16 log2 2 = dx dy (67) 0 0 x + 1 y + 1 xy + 1 5 3 Iterative algorithms for π p • (The Archimedes iteration).
Load more

Recommended publications
  • The Enigmatic Number E: a History in Verse and Its Uses in the Mathematics Classroom
    To appear in MAA Loci: Convergence The Enigmatic Number e: A History in Verse and Its Uses in the Mathematics Classroom Sarah Glaz Department of Mathematics University of Connecticut Storrs, CT 06269 [email protected] Introduction In this article we present a history of e in verse—an annotated poem: The Enigmatic Number e . The annotation consists of hyperlinks leading to biographies of the mathematicians appearing in the poem, and to explanations of the mathematical notions and ideas presented in the poem. The intention is to celebrate the history of this venerable number in verse, and to put the mathematical ideas connected with it in historical and artistic context. The poem may also be used by educators in any mathematics course in which the number e appears, and those are as varied as e's multifaceted history. The sections following the poem provide suggestions and resources for the use of the poem as a pedagogical tool in a variety of mathematics courses. They also place these suggestions in the context of other efforts made by educators in this direction by briefly outlining the uses of historical mathematical poems for teaching mathematics at high-school and college level. Historical Background The number e is a newcomer to the mathematical pantheon of numbers denoted by letters: it made several indirect appearances in the 17 th and 18 th centuries, and acquired its letter designation only in 1731. Our history of e starts with John Napier (1550-1617) who defined logarithms through a process called dynamical analogy [1]. Napier aimed to simplify multiplication (and in the same time also simplify division and exponentiation), by finding a model which transforms multiplication into addition.
    [Show full text]
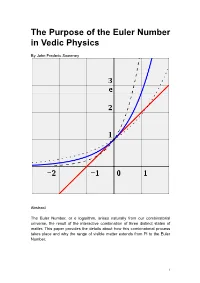
  • Euler Number in Vedic Physics
    The Purpose of the Euler Number in Vedic Physics By John Frederic Sweeney Abstract The Euler Number, or e logarithm, arises naturally from our combinatorial universe, the result of the interactive combination of three distinct states of matter. This paper provides the details about how this combinatorial process takes place and why the range of visible matter extends from Pi to the Euler Number. 1 Table of Contents Introduction 3 Wikipedia on the Euler Number 5 Vedic Physics on the Euler Number 6 Conclusion 8 Bibliography 9 2 Introduction The author posted a few papers on Vixra during 2013 which made statements about Pi and the Euler Number that lacked support. This paper offers the support for those statements. Since the explanation is mired, twisted and difficult to follow, the author wished to make other aspects of Vedic Particle Physics clear. This paper begins with Wikipedia on Euler, then to the Vedic Explanation. This paper, along with Why Pi? Which explains the reason why Pi carries such importance in a combinatorial world, should make it easier for readers to grasp the fundamental concepts of Vedic Particle Physics. Essentially, three states of matter exist in a combinatorial world, the axes of the states run from Pi to the Euler number. The simple formula of n + 1 suggests Pascal’s Triangle or Mount Meru, and the author has published a paper on this theme about Clifford Algebras, suggesting them as a most useful tool in a combinatorial universe. Someone once said that only those with clear understanding can explain things clearly and simply to others.
    [Show full text]
  • The Exponential Constant E
    The exponential constant e mc-bus-expconstant-2009-1 Introduction The letter e is used in many mathematical calculations to stand for a particular number known as the exponential constant. This leaflet provides information about this important constant, and the related exponential function. The exponential constant The exponential constant is an important mathematical constant and is given the symbol e. Its value is approximately 2.718. It has been found that this value occurs so frequently when mathematics is used to model physical and economic phenomena that it is convenient to write simply e. It is often necessary to work out powers of this constant, such as e2, e3 and so on. Your scientific calculator will be programmed to do this already. You should check that you can use your calculator to do this. Look for a button marked ex, and check that e2 =7.389, and e3 = 20.086 In both cases we have quoted the answer to three decimal places although your calculator will give a more accurate answer than this. You should also check that you can evaluate negative and fractional powers of e such as e1/2 =1.649 and e−2 =0.135 The exponential function If we write y = ex we can calculate the value of y as we vary x. Values obtained in this way can be placed in a table. For example: x −3 −2 −1 01 2 3 y = ex 0.050 0.135 0.368 1 2.718 7.389 20.086 This is a table of values of the exponential function ex.
    [Show full text]
  • Crystals of Golden Proportions
    THE NOBEL PRIZE IN CHEMISTRY 2011 INFORMATION FOR THE PUBLIC Crystals of golden proportions When Dan Shechtman entered the discovery awarded with the Nobel Prize in Chemistry 2011 into his notebook, he jotted down three question marks next to it. The atoms in the crystal in front of him yielded a forbidden symmetry. It was just as impossible as a football – a sphere – made of only six- cornered polygons. Since then, mosaics with intriguing patterns and the golden ratio in mathematics and art have helped scientists to explain Shechtman’s bewildering observation. “Eyn chaya kazo”, Dan Shechtman said to himself. “There can be no such creature” in Hebrew. It was the morning of 8 April 1982. The material he was studying, a mix of aluminum and manganese, was strange- looking, and he had turned to the electron microscope in order to observe it at the atomic level. However, the picture that the microscope produced was counter to all logic: he saw concentric circles, each made of ten bright dots at the same distance from each other (fgure 1). Shechtman had rapidly chilled the glowing molten metal, and the sudden change in temperature should have created complete disorder among the atoms. But the pattern he observed told a completely different story: the atoms were arranged in a manner that was contrary to the laws of nature. Shechtman counted and recounted the dots. Four or six dots in the circles would have been possible, but absolutely not ten. He made a notation in his notebook: 10 Fold??? BRIGHT DOTS will DARKNESS results appear where wave where crests and crests intersect and troughs meet and reinforce each other.
    [Show full text]
  • List of Mathematical Symbols by Subject from Wikipedia, the Free Encyclopedia
    List of mathematical symbols by subject From Wikipedia, the free encyclopedia This list of mathematical symbols by subject shows a selection of the most common symbols that are used in modern mathematical notation within formulas, grouped by mathematical topic. As it is virtually impossible to list all the symbols ever used in mathematics, only those symbols which occur often in mathematics or mathematics education are included. Many of the characters are standardized, for example in DIN 1302 General mathematical symbols or DIN EN ISO 80000-2 Quantities and units – Part 2: Mathematical signs for science and technology. The following list is largely limited to non-alphanumeric characters. It is divided by areas of mathematics and grouped within sub-regions. Some symbols have a different meaning depending on the context and appear accordingly several times in the list. Further information on the symbols and their meaning can be found in the respective linked articles. Contents 1 Guide 2 Set theory 2.1 Definition symbols 2.2 Set construction 2.3 Set operations 2.4 Set relations 2.5 Number sets 2.6 Cardinality 3 Arithmetic 3.1 Arithmetic operators 3.2 Equality signs 3.3 Comparison 3.4 Divisibility 3.5 Intervals 3.6 Elementary functions 3.7 Complex numbers 3.8 Mathematical constants 4 Calculus 4.1 Sequences and series 4.2 Functions 4.3 Limits 4.4 Asymptotic behaviour 4.5 Differential calculus 4.6 Integral calculus 4.7 Vector calculus 4.8 Topology 4.9 Functional analysis 5 Linear algebra and geometry 5.1 Elementary geometry 5.2 Vectors and matrices 5.3 Vector calculus 5.4 Matrix calculus 5.5 Vector spaces 6 Algebra 6.1 Relations 6.2 Group theory 6.3 Field theory 6.4 Ring theory 7 Combinatorics 8 Stochastics 8.1 Probability theory 8.2 Statistics 9 Logic 9.1 Operators 9.2 Quantifiers 9.3 Deduction symbols 10 See also 11 References 12 External links Guide The following information is provided for each mathematical symbol: Symbol: The symbol as it is represented by LaTeX.
    [Show full text]
  • Transcendence of Generalized Euler Constants Author(S): M
    Transcendence of Generalized Euler Constants Author(s): M. Ram Murty, Anastasia Zaytseva Source: The American Mathematical Monthly, Vol. 120, No. 1 (January 2013), pp. 48-54 Published by: Mathematical Association of America Stable URL: http://www.jstor.org/stable/10.4169/amer.math.monthly.120.01.048 . Accessed: 27/11/2013 11:47 Your use of the JSTOR archive indicates your acceptance of the Terms & Conditions of Use, available at . http://www.jstor.org/page/info/about/policies/terms.jsp . JSTOR is a not-for-profit service that helps scholars, researchers, and students discover, use, and build upon a wide range of content in a trusted digital archive. We use information technology and tools to increase productivity and facilitate new forms of scholarship. For more information about JSTOR, please contact [email protected]. Mathematical Association of America is collaborating with JSTOR to digitize, preserve and extend access to The American Mathematical Monthly. http://www.jstor.org This content downloaded from 14.139.163.28 on Wed, 27 Nov 2013 11:47:04 AM All use subject to JSTOR Terms and Conditions Transcendence of Generalized Euler Constants M. Ram Murty and Anastasia Zaytseva Abstract. We consider a class of analogues of Euler’s constant γ and use Baker’s theory of linear forms in logarithms to study its arithmetic properties. In particular, we show that with at most one exception, all of these analogues are transcendental. 1. INTRODUCTION. There are two types of numbers: algebraic and transcenden- tal. A complex number is called algebraic if it is a root of some algebraic equation with integer coefficients.
    [Show full text]
  • Π-The Transcendental Number
    MAT-KOL (Banja Luka) ISSN: 0354-6969 (p), ISSN: 1986-5228 (o) http://www.imvibl.org/dmbl/dmbl.htm Vol. XXIII (1)(2017), 61-66 DOI: 10.7251/MK1701061G π-THE TRANSCENDENTAL NUMBER Karthikeya Gounder Abstract. In this paper π is expressed in a new way, rather than, a series converging to get the exact value. This formula relates the mathematical constant π with trigonometric tan. 1. Introduction The number π is a mathematical constant, the ratio of a circle's circumference to its diameter. It is represented by the Greek letter π since the mid-XVIIIth century. It was calculated to seven digits using geometrical techniques in Chinese mathematics and to about five in Indian mathematics in the fifth century AD. π has a history of more than 1800 years. Hundreds of mathematicians had discovered many formulas to calculate the value of π. The historically first exact formula for π is based on infinite series, was not available until a millennium later, when in the 14th century the Madhava - Leibniz series was discovered in Indian mathematics [1]. Few years later, mathematicians and computer scientists discovered new approaches that, when combined with increasing computational power, extended the decimal representation of π to many trillions of digits after the decimal point [2]. It is an irrational number, so π cannot be expressed exactly as a fraction and it is also a transcendental numbers- A number that is not the root of any non- zero polynomial having rational coefficients. Its decimal representation never ends. Fractions such as 22/7 are commonly used to approximate.
    [Show full text]
  • Measurement of Mathematical Constant P and Physical Quantity Pi
    Journal of Applied Mathematics and Physics, 2016, 4, 1899-1905 http://www.scirp.org/journal/jamp ISSN Online: 2327-4379 ISSN Print: 2327-4352 Measurement of Mathematical Constant π and Physical Quantity Pi Milan Perkovac University of Applied Sciences, Zagreb, Croatia How to cite this paper: Perkovac, M. (2016) Abstract Measurement of Mathematical Constant π and Physical Quantity Pi. Journal of App- Instead of calculating the number π in this article special attention is paid to the me- lied Mathematics and Physics, 4, 1899- thod of measuring it. It has been found that there is a direct and indirect measure- 1905. ment of that number. To perform such a measurement, a selection was made of some http://dx.doi.org/10.4236/jamp.2016.410192 mathematical and physical quantities which within themselves contain a number π. π Received: September 13, 2016 One such quantity is a straight angle Pi, which may be expressed as Pi = rad. By Accepted: October 17, 2016 measuring the angle, using the direct method, we determine the number π as π = Published: October 20, 2016 arccos(−1). To implement an indirect measurement of the number π, a system con- sisting of a container with liquid and equating it with the measuring pot has been Copyright © 2016 by author and conceived. The accuracy of measurement by this method depends on the precision Scientific Research Publishing Inc. This work is licensed under the Creative performance of these elements of the system. Commons Attribution International License (CC BY 4.0). Keywords http://creativecommons.org/licenses/by/4.0/ Pi, Greek Letter π, Angle Measurement, Measuring Pot, Radian Open Access 1.
    [Show full text]
  • List of Numbers
    List of numbers This is a list of articles aboutnumbers (not about numerals). Contents Rational numbers Natural numbers Powers of ten (scientific notation) Integers Notable integers Named numbers Prime numbers Highly composite numbers Perfect numbers Cardinal numbers Small numbers English names for powers of 10 SI prefixes for powers of 10 Fractional numbers Irrational and suspected irrational numbers Algebraic numbers Transcendental numbers Suspected transcendentals Numbers not known with high precision Hypercomplex numbers Algebraic complex numbers Other hypercomplex numbers Transfinite numbers Numbers representing measured quantities Numbers representing physical quantities Numbers without specific values See also Notes Further reading External links Rational numbers A rational number is any number that can be expressed as the quotient or fraction p/q of two integers, a numerator p and a non-zero denominator q.[1] Since q may be equal to 1, every integer is a rational number. The set of all rational numbers, often referred to as "the rationals", the field of rationals or the field of rational numbers is usually denoted by a boldface Q (or blackboard bold , Unicode ℚ);[2] it was thus denoted in 1895 byGiuseppe Peano after quoziente, Italian for "quotient". Natural numbers Natural numbers are those used for counting (as in "there are six (6) coins on the table") and ordering (as in "this is the third (3rd) largest city in the country"). In common language, words used for counting are "cardinal numbers" and words used for ordering are
    [Show full text]
  • A Reflection of Euler's Constant and Its Applications
    2012 International Transaction Journal of Engineering, Management, & Applied Sciences & Technologies. International Transaction Journal of Engineering, Management, & Applied Sciences & Technologies http://TuEngr.com, http://go.to/Research A Reflection of Euler’s Constant and Its Applications a* a Spyros Andreou and Jonathan Lambright a Department of Engineering Technology and Mathematics, Savannah State University, Savannah, GA 31404, USA A R T I C L E I N F O A B S T R A C T Article history: One of the most fascinating and remarkable formulas Received 23 May 2012 Received in revised form existing in mathematics is the Euler Formula. It was formulated 06 July 2012 in 1740, constituting the main factor to reason why humankind can Accepted 08 July 2012 advance in science and mathematics. Accordingly, this research Available online 09 July 2012 will continue investigating the potentiality of the Euler Formula or Keywords: "the magical number e." The goal of the present study is to number e, further assess the Euler formula and several of its applications such approximation, as the compound interest problem, complex numbers, limit, trigonometry, signals (electrical engineering), and Ordinary complex exponential, Differential Equations. To accomplish this goal, the Euler compound interest. Formula will be entered into the MATLAB software to obtain several plots representing the above applications. The importance of this study in mathematics and engineering will be discussed, and a case study on a polluted lake will be formulated. 2012 International Transaction Journal of Engineering, Management, & Applied Sciences & Technologies. 1. Introduction –History The purpose of this study is to explore the evolution of number e.
    [Show full text]
  • A Short History of Π Formulas
    A short history of π formulas David H. Bailey∗ November 8, 2016 Abstract This note presents a short history mathematical formulas involving the mathematical constant π, and how they have been used in mathematical research through the ages. 1 Background The mathematical constant we know as π = 3:141592653589793 ::: is undeniably the most famous and ar- guably the most important mathematical constant. Mathematicians since the days of Euclid and Archimedes have computed its numerical value in a search for answers to questions such as: (a) is π a rational number? (i.e., is π the ratio of two whole numbers?) (b) does π satisfy some algebraic equation with integer coefficients? (c) is π simply related to other constants of mathematics? Some of these questions were eventually resolved: In the late 1700s, Lambert and Legendre proved (by means of a continued fraction argument) that π is irrational, which explains why its digits never repeat. Then in 1882 Lindemann proved that π is transcendental, which means that π is not the root of any algebraic equation with integer coefficients. Lindemann's proof also settled, in the negative, the ancient Greek question of whether a circle could be \squared," or, in other words, whether one could construct, using ruler and compass, a square with the same area as a given circle. This cannot be done, because (as it is easy to show using high school algebra) any length constructible by rule and compass procedures is given by a finite combination of add, subtract, multiply, divide and square root operations, which thus is algebraic.
    [Show full text]
  • Math Notation Handout
    Greek Letters Common Usages Αα Alpha α: Constant in regression/statistics: y = α + βx + ε; also type I error Ββ Beta β: Coefficient in regression/statistics, often subscripted to indicate different coefficients: y = α + β1x1 + β2x2 + ε; also type II error; related, 1 – β is called the “power” of a statistical test. Γγ Gamma Γ: A particular statistical distribution; also used to denote a game. ∆δ Delta ∆y y1 − y2 ∆: Means “change” or “difference”, as in the equation of a line’s slope: = . ∆x x1 − x2 δ: Known in game theory as the “discount parameter” and is used for repeated games. Εε Epsilon ε: “Error term” in regression/statistics; more generally used to denote an arbitrarily small, positive number. ∈ (Variant Epsilon) This version of epsilon is used in set theory to mean “belongs to” or “is in the set of”: x ∈ X; similarly used to indicate the range of a parameter: x ∈ [0, 1]. “x ∉ ∅” means “the element x does not belong to the empty set”. Ζζ Zeta Ηη Eta Θθ Theta θ: The fixed probability of success parameter in a Binomial Distribution and related distributions. ϑ (Script Theta) Ιι Iota Κκ Kappa Λλ Lambda λ= nθ: Parameter in the Poisson Distribution. Μµ Mu µ: In statistics, the mean of a distribution. In game theory, often used as the probability of belief. Νν Nu Ξξ Xi Οο Omicron Ππ Pi 5 ∏: Product symbol, as in ∏i = 60 . i=3 π: Mathematical constant (3.14159…); also used in game theory to denote an actor’s belief as a probability. Ρρ Rho ρ: Correlation coefficient in some statistical analyses.
    [Show full text]