DOCSLIB.ORG

Section Is Famous Birth Place of Goddess Sita. It Is

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Section Is Famous Birth Place of Goddess Sita. It Is GENERAL INFORMATION INTRODUCTION Samastipur Division, one of the five divisions of EAST CENTRAL RAILWAY, came into existence in the year 1969, is situated on the bank of Budhi Gandak river. Samastipur town is also a district headquarter, comprising of many sections of old Oudh Tirhut Railway apart from being a centre of rich cultural heritage of Mithila region. Samastipur division serves 15 densely populated Districts of North Bihar with a multi-gauge network comprising of both Broad-gauge and Metre-gauge. On the north side, the Division borders with Nepal. Raxaul, Jaynagar and Laukaha Bazar are important rail-heads for Nepal-bound traffic. PLACES OF TOURIST IMPORTANCE Samastipur division covers a number of tourist places of historical importance. Some of these are: Sitamarhi Madhubani: JANAKPUR DHAM Situated DBG-NKE It was the Capital of the section is famous kingdom of Raja Janak. for being the It is a cultural center of "Sita Swayambar" was birth place of Mithilanchal and is famous for held here. It is situated in its rich cultural heritage and Nepal and is connected Goddess Sita. It is Madhubani paintings. The by rail from Jaynagar and also directly famous "Shastrartha" with by road from Sitamarhi connected with Mandan Mishra and “Adi Guru” and Janakpur Road Muzaffarpur Shankaracharya was held in a stations. It is the place nearby birthplace of Janaki, or Darbhanga It is Commissionary town Sita, daughter of King having two universities viz. Janak.Janakpur, Sanskrit University and historically called Lalit Narayan Mithila Mithilanchal, is the centre University. Several palaces of of the ancient Maithili ancient king and temples are culture, which has its own of tourist interest are available language and script. here. Valmikinagar: There is "Valmiki Ashram" near Valmiki Nagar station in the name of Maharshi Valmiki. It is believed that “Lava” and “Kush” the mighty sons of Lord Rama were born and brought up in the above Ashram. Also famous for Tiger Project. 1 West Champaran तपु . नंदनगढ़ अशोक तम,् लौरया भतहरबा आम With district headquarters at Motihari."Ashoka Stambha" of King Ashok era is worth seeing at Louria and Bodh Stup,Nandangarh near Narkatiaganj. This district is also famous for Bhitiharva Ashram.Bhitiharva is a village at about 17 Km from Narkatiaganj Station where Gandhiji started his freedom movement that came to be known as 'Champaran Satyagraha' in India history. Bhitiharva Ashram was originally known as Kasturba Sewa Kendra, it was inaugurated by Mahatma Gandhi on 20th November 1917 as a basic school to share knowledge with tribal women and girls later it was hub for freedom fighter.Mahatma Gandhi had launched the Non-co-operation movement in India for the first time from here. During this period he stayed at Bhitiharva Ashram which is now served with a Halt station near Narkatiaganj in Narkatiaganj - Bhikhnathoree MG section. East Champaran अशोक तभ अरेराज गाँधी मतृ तभ एवं संहालय,मोतीहार नेपाल वेशमाग With district headquarters at Motihari."Ashoka Stambha" of King Ashok era is worth seeing at Areraj,Gandhi Memorial Statue and Museum at Motihari.Raxaul entry point of Nepal is also situated in this District. It is a famous pilgrimage of lord Mahadeo in the country. It is situated at a distance of 8 km from Madhepura and about 30 Km from Saharsa Station and is renowned for its historical and religious importance.Here Devotes not only from Bihar but also from other parts of the country including the neighboring country Nepal come to singheshwar sthan for the worship of lord Shiva. Mahashivratri mela of singheshwar sthan is famous in संहेवर थान मधेपराु Bihar and Nepal also. It is situated on the bank of river Koshi, between the stations Badlaghat and Dhamaraghat on Mansi-Saharsa rail line. Temples of Ma Katyayani , as well as of Ram, Lakshman and Ma Janaki is situated at this place. Every Monday and Friday , large number of devotees come to this place for offering puja. As per the local folk traditions, Ma Katyayani is worshiped as Lok Devi- Devi of Milk कायान मंदर धमाराघाट Cattles. That is why devotees offer raw milk to the deity. 2 GENERAL INFORMATION ABOUT THE DIVISION GEOGRAPHY & HISTORY Date of Beginning : 1969 Situated : On Bank of Budhi Gandak Region : Mithilanchal Districts Served : 15 Nos. Sequence wise Governing Railway . Tirhut State Railway (TSR) . Bengal Nagpur Western Railway (BNWR) . Oudh Tirhut Railway (OTR) . North Eastern Railway (NER) . East Central Railway (ECR) Major Rivers . Kosi . Bagmati . Budhi Gandak . Kamla Balan . Adhwara Group . Lakhandeyee . Sikrana Nepal Border Heads . Raxaul . Jaynagar . Laukha Bazar . Forbesganj . Bairgania . Raghopur Tourist Place . Sitamarhi : Birth place of Goddess Sita. Jankapur road : Sita Swayambar . Madhubani : Madhubani painting . Darbhanga : Postal Trg.Institute . Valmiki Nagar: Valmiki Ashram and Tiger century. Champaran : Ashoka Stambh at Lauria . Bithiharwa Ashram : Non-Co-operation movement in India launched by father of nation, M.K.Gandhi. 3 BACKGROUND Samastipur division serves 15 densely populated districts of North Bihar comprising East Champaran, West Champaran, Shivhar, Sitamarhi, Madhubani, Darbhanga, Samastipur, Muzaffarpur, Khagaria, Begusarai, Saharsa, Supaul, Madhepura, Araria and Purnea. TRACK/ROUTE KILOMETRES : Blocked for Particulars BG MG Total GC Route Kilometers 788.13 184.24 159.76 1132.13 Track Kilometers 872.75 237.95 192.55 1303.25 NUMBER OF BRIDGES : Type BG MG Total Important Bridges 14 01 15 Major Bridges 169 100 269 Minor Bridges 642 434 1076 Total 825 535 1360 LEVEL CROSSINGS : Class Gauge C C Spl. A B D Total (Manned) (Unmanned) BG 11 16 45 277 256 0 605 MG 2 4 11 56 233 9 315 Total 13 20 56 333 489 9 920 TRACK STRUCTURE : Rail Sleeper Section Wooden 52 Kg 90R 75R 60R Total PSC CST-9 ST Total /Mix BG 788.13 00 00 00 788.13 788.13 00 00 00 788.13 MG 0 31.34 49.5 103.4 184.24 0 107.88 19.1 57.26 184.24 Block- ed for - - - - 159.76 - - - - 159.76 GC Total 788.13 31.34 49.5 103.4 1132.13 788.13 107.88 19.1 57.26 1132.13 4 .
Load more

Recommended publications
  • AC with District Dist
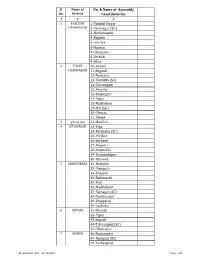
    Sl Name of No. & Name of Assembly No. District Constituencies 1 2 3 1 PASCHIM 1-Valmiki Nagar CHAMPARAN 2-Ramnagar (SC) 3-Narkatiaganj 4-Bagaha 5-Lauriya 6-Nautan 7-Chanpatia 8-Bettiah 9-Sikta 2 PURVI 10-Raxaul CHAMPARAN 11-Sugauli 12-Narkatia 13-Harsidhi (SC) 14-Govindganj 15-Kesaria 16-Kalyanpur 17-Pipra 18-Madhuban 19-Motihari 20-Chiraia 21-Dhaka 3 SHEOHAR 22-Sheohar 4 SITAMARHI 23-Riga 24-Bathnaha (SC) 25-Parihar 26-Sursand 27-Bajpatti 28-Sitamarhi 29-Runnisaidpur 30-Belsand 5 MADHUBANI 31-Harlakhi 32- Benipatti 33-Khajauli 34-Babubarhi 35-Bisfi 36-Madhubani 37-Rajnagar (SC) 38-Jhanjharpur 39-Phulparas 40-Laukaha 6 SUPAUL 41-Nirmali 42-Pipra 43-Supaul 44-Triveniganj (SC) 45-Chhatapur 7 ARARIA 46-Narpatganj 47-Raniganj (SC) 48-Forbesganj AC with district Dist. - AC (English) Page 1 of 6 Sl Name of No. & Name of Assembly No. District Constituencies 1 2 3 49-Araria 50-Jokihat 51-Sikti 8 KISHANGANJ 52-Bahadurganj 53-Thakurganj 54-Kishanganj 55-Kochadhaman 9 PURNIA 56-Amour 57-Baisi 58-Kasba 59-Banmankhi (SC) 60-Rupauli 61-Dhamdaha 62-Purnia 10 KATIHAR 63-Katihar 64-Kadwa 65-Balrampur 66-Pranpur 67-Manihari (ST) 68-Barari 69-Korha (SC) 11 MADHEPURA 70-Alamnagar 71-Bihariganj 72-Singheshwar (SC) 73-Madhepura 12 SAHARSA 74-Sonbarsha (SC) 75-Saharsa 76-Simri Bakhtiarpur 77-Mahishi 13 DARBHANGA 78-Kusheshwar Asthan (SC) 79-Gaura Bauram 80-Benipur 81-Alinagar 82-Darbhanga Rural 83-Darbhanga 84-Hayaghat 85-Bahadurpur 86-Keoti 87-Jale 14 MUZAFFARPUR 88-Gaighat 89-Aurai 90-Minapur 91-Bochaha (SC) 92-Sakra (SC) 93-Kurhani 94-Muzaffarpur 95-Kanti 96-Baruraj AC with district Dist.
    [Show full text]
  • Karnali Excursions, Nepal
    1 Karnali Excursions Kailash Yatra 2020 1 ç Om Namah Shivaya Karnali Excursions, Nepal Kailash - Mansarovar Yatra & Other Himalayan Pilgrimages 2020 Join with us for the journey of a lifetime to experience Satyam, Shivam and Sundaram www.karnaliexcursions.com Karnali Excursions Kailash Yatra 2020 2 Table of Contents: SN. Contents Page No. 1. About Kailash & Our Services 3 2. Kailash-Mansarovar & Other Yatra Maps 4 3. Fixed Departure Dates of Kailash-Mansarovar Yatra & Other Pilgrimages 5 - 6 4. Kailash-Mansarovar Yatra only 7 5. Kailash-Mansarovar Yatra with Muktinath Darshan 8 6. Kailash-Mansarovar with Muktinath-Janakpur Dham-Valmiki Ashram-Devghat-Lumbini 9 7. About Muktinath, Damodar Kunda, Janakpur Dham, Devghat, Valmiki Ashram, Lumbini and Chitwan National Park 10 - 13 8. Kailash-Mansarovar with Chardham Yatra 14 9. Kailash-Mansarovar with Shree Amarnath Yatra 15 10. Shree Amarnath Yatra only 16 - 17 11. Chardham Yatra only 18 - 19 12. Jyotirling Darshan Yatra 20 - 21 13. Narmad Parikrama-Arunachal Hill-Pancha Mahabhoot Yatra 22 14. Swaminarayan Trail Tour 23 - 24 15. World-wide Contact Details 26 2 Karnali Excursions Kailash Yatra 2020 3 Om Namah Shivaya! “As the dew is dried up by the morning sun, so are the sins of human beings by the sight of Mt. Kailash and Lake Manasarovar” - Skanda Purana” Holy Mount Kailash is believed as an important pilgrimage destination as well as a power point, where it is possible to gain inspiration and energy to transform oneself from this physical to higher spiritual level. The custom of circumambulating Mount Kailash is believed to purify the soul and cultivate in each visiting pilgrim the ability to experience the divinity.
    [Show full text]
  • Sita Ram Baba
    सीता राम बाबा Sītā Rāma Bābā סִיטָ ה רְ אַמָ ה בָבָ ה Bābā بَابَا He had a crippled leg and was on crutches. He tried to speak to us in broken English. His name was Sita Ram Baba. He sat there with his begging bowl in hand. Unlike most Sadhus, he had very high self- esteem. His eyes lit up when we bought him some ice-cream, he really enjoyed it. He stayed with us most of that evening. I videotaped the whole scene. Churchill, Pola (2007-11-14). Eternal Breath : A Biography of Leonard Orr Founder of Rebirthing Breathwork (Kindle Locations 4961-4964). Trafford. Kindle Edition. … immortal Sita Ram Baba. Churchill, Pola (2007-11-14). Eternal Breath : A Biography of Leonard Orr Founder of Rebirthing Breathwork (Kindle Location 5039). Trafford. Kindle Edition. Breaking the Death Habit: The Science of Everlasting Life by Leonard Orr (page 56) ראמה راما Ράμα ראמה راما Ράμα Rama has its origins in the Sanskrit language. It is used largely in Hebrew and Indian. It is derived literally from the word rama which is of the meaning 'pleasing'. http://www.babynamespedia.com/meaning/Rama/f Rama For other uses, see Rama (disambiguation). “Râm” redirects here. It is not to be confused with Ram (disambiguation). Rama (/ˈrɑːmə/;[1] Sanskrit: राम Rāma) is the seventh avatar of the Hindu god Vishnu,[2] and a king of Ayodhya in Hindu scriptures. Rama is also the protagonist of the Hindu epic Ramayana, which narrates his supremacy. Rama is one of the many popular figures and deities in Hinduism, specifically Vaishnavism and Vaishnava reli- gious scriptures in South and Southeast Asia.[3] Along with Krishna, Rama is considered to be one of the most important avatars of Vishnu.
    [Show full text]
  • West Champaran Introduction
    DISTRICT PROFILE WEST CHAMPARAN INTRODUCTION West Champaran is an administrative district in the state of Bihar. West Champaran district was carved out of old champaran district in the year 1972. It is part of Tirhut division. West Champaran is surrounded by hilly region of Nepal in the North, Gopalganj & part of East Champaran district in the south, in the east it is surrounded by East Champaran and in the west Padrauna & Deoria districts of Uttar Pradesh. The mother-tongue of this region is Bhojpuri. The district has its border with Nepal, it has an international importance. The international border is open at five blocks of the district, namely, Bagha- II, Ramnagar, Gaunaha, Mainatand & Sikta, extending from north- west corner to south–east covering a distance of 35 kms . HISTORICAL BACKGROUND The history of the district during the late medieval period and the British period is linked with the history of Bettiah Raj. The British Raj palace occupies a large area in the centre of the town. In 1910 at the request of Maharani, the palace was built after the plan of Graham's palace in Calcutta. The Court Of Wards is at present holding the property of Bettiah Raj. The rise of nationalism in Bettiah in early 20th century is intimately connected with indigo plantation. Raj Kumar Shukla, an ordinary raiyat and indigo cultivator of Champaran met Gandhiji and explained the plight of the cultivators and the atrocities of the planters on the raiyats. Gandhijii came to Champaran in 1917 and listened to the problems of the cultivators and the started the movement known as Champaran Satyagraha movement to end the oppression of the British indigo planters.
    [Show full text]
  • Bihar Eng 21 to 30 Set
    Achievements of Railways LoPN Hkkjr in ,d dne LoPNrk dh vksj Nawada Lok Sabha Constituency ge lc dk gks ,d gh ukjkA lkiQ lqFkjk gks jsy gekjkAA of Bihar East Central Railway, Hajipur Works / Projects Completed : l Provision of ROB in lieu of level crossing l Stoppage of Train no. 15619/15620 no. 33 in Nawada Yard. l Gaya - Kamakhya Express (Weekly) at Provision of Limited Height Subways in lieu of level crossings no. 27, 29, 17, 19, Nawada and Warisaliganj Stations. 40 and 50. l Extension of Loop Line at Nawada Works / Projects planned in future : Station. l New Line between Koderma - Tilaiya. l Development of Nawada, Sheikh- pura, l New Line between Nawada - Lakhimpur Warisaliganj, Hisua as Adarsh Station. l Improvement work of circulating area, l Provision of benches and sheds at extension of FOB, renovation of station building, extension of PF No. 1, 2nd various halt stations. class waiting hall, Pay & Use Toilet l Electrification of Kiul - Gaya Section. along with passenger amenities at l Provision of additional loop line at Warisaliganj Station. Sheikhpura Station. l Improvement work of circulating area, replacement of old FOB by new 3 m l Improvement work of approach road wide FOB, renovation of station building and basic infrastructure at manned LCs along with passenger amenities at in Nawada. Nawada Station. l Provision of water supply with new deep l 30 bed running room at Tilaiya. tubewell with pipe line at Sheikhpura and Nawada Stations. l Improvement of various Halt stations Lean to shed with benches. Ongoing Works / Projects : l Doubling of Kiul - Gaya Section.
    [Show full text]
  • Break-Up of Contesting Candidates
    1- Dhanaha 1. No. and Name of the Constituency : : 1 - Dhanaha 2. Form Unique Serial Number (FUSN) Prefix : : KMQ 3. Type of Constituency (Gen/SC/ST) : : GEN 4. Name and Designation of the Returning Officer : Sri M.Jaya Deputy Director, Consolidation, West Champaran 5. Date of Poll 13/11/05 6. Date of Repoll (if any) - 7. Date of Commencement of Counting 22-Nov-2005 8. Date of Declaration of Result 22-Nov-2005 9. Data About Polling Stations : Regular Polling Stations - 129 Average No. of Electors Per Polling Station - 876 Auxilliary Polling Stations 9 Average No. of Voters Per Polling Station - 429 Total Polling Stations 138 10. Data About Candidates : Men Women Total No. of Nomination Filed : 11 0 11 No. of Nomination Rejected : 0 0 0 No. of Nomination found correct after scrutiny : 11 0 11 No. of Withdrawals : 0 0 0 No. of Contesting Candidates : 11 0 11 No. of Candidates who forfeited their deposits : 8 0 8 Break-Up of Contesting Candidates National Parties : 1 0 1 State Parties : 4 0 4 Registered (Unrecognised) Parties : 2 0 2 Independents : 4 0 4 11. Details about Electors : General Service Total Male 68,015 5 68,020 Female 52,823 3 52,826 Total 120,838 8 120,846 12. Details about Voters : General Postal Total Male 33,424 0 33,424 Female 25,829 0 25,829 Total 59,253 0 59,253 Rejected Votes 0 Missing Votes 0 1- Dhanaha 13. Names of Contesting Candidates and their details : Sl. Candidate Name & Address SC/ Sex Party Symbol Final No.
    [Show full text]
  • ANSWERED ON:22.11.2012 RAILWAY LINES UNDER ECR, HAZIPUR Singh Shri Mahabali
    GOVERNMENT OF INDIA RAILWAYS LOK SABHA UNSTARRED QUESTION NO:90 ANSWERED ON:22.11.2012 RAILWAY LINES UNDER ECR, HAZIPUR Singh Shri Mahabali Will the Minister of RAILWAYS be pleased to state: (a) the total length of railway lines under East Central Railway (ECR), Hajipur, gauge-wise; (b) the total length of gauge conversion completed during the last three years and the current year under the ECR, year-wise; (c) the details and the present status of ongoing gauge conversion works under the ECR; and (d) the time frame set for completion of these projects? Answer MINISTER OF STATE IN THE MINISTRY OF RAILWAYS (SHRI ADHIR RANJAN CHOWDHURY) (a) to (d): A Statement is laid on the Table of the House. STATEMENT REFERRED TO IN REPLY TO PARTS (a) TO (d) OF UNSTARRED QUESTION NO. 90 BY SHRI MAHABALI SINGH TO BE ANSWERED IN LOK SABHA ON 22.11.2012 REGARDING RAILWAY LINES UNDER ECR, HAZIPUR. (a): On East Central Railway, length of railway lines, in terms of route kilometres, is 3,217.91 and 438.31 on Broad Gauge and Metre Gauge, respectively. There is no Narrow Gauge in East Central Railway. (b): During last three years, i.e. 2009-10 to 2011-12, 110 kilometres of Gauge Conversion o n East Central Railway has been completed. (c): Details of ongoing Gauge Conversion Projects on East Central Railway is as under: S. Name of Length in Latest Expendi-ture Present Status/ No. Project kilometres Anticipated upto Target Cost March'12 wherever (Rs. in (Rs.in fixed crores) crores) 1 Jaynagar- 69 470 0.32 Work transferred Bijalpura, to IRCON for including execution.
    [Show full text]
  • West Champaran District, Bihar State
    भूजल सूचना पुस्तिका पस्चचमी च륍पारण स्जला, बिहार Ground Water Information Booklet West Champaran District, Bihar State ADMINISTRATIVE MAP WEST CHAMPARAN DISTRICT, BIHAR N 0 5 10 15 20 Km Scale Masan R GAONAHA SIDHAW RAMNAGAR PIPRASI MAINATAND BAGAHA NARKATIAGANJ LAURIYA MADHUBANI SIKTA BHITAHA CHANPATTIA GandakJOGAPATTI R MANJHAULIA District Boundary BETTIAH Block Boundary THAKRAHA BAIRIA Road Railway NAUTAN River Block Headquarter के न्द्रीय भमू मजल िो셍 ड Central Ground water Board Ministry of Water Resources जल संसाधन मंत्रालय (Govt. of India) (भारि सरकार) Mid-Eastern Region Patna मध्य-पर्वू ी क्षेत्र पटना मसिंिर 2013 September 2013 1 Prepared By - Dr. Rakesh Singh, Scientist – ‘B’ 2 WEST CHAMPARAN, BIHAR S. No CONTENTS PAGE NO. 1.0 Introduction 6 - 10 1.1 Administrative details 1.2 Basin/sub-basin, Drainage 1.3 Irrigation Practices 1.4 Studies/Activities by CGWB 2.0 Climate and Rainfall 11 3.0 Geomorphology and Soils 11 - 12 4.0 Ground Water Scenario 12 – 19 4.1 Hydrogeology 4.2 Ground Water Resources 4.3 Ground Water Quality 4.4 Status of Ground Water Development 5.0 Ground Water Management Strategy 19 – 20 5.1 Ground Water Development 5.2 Water Conservation and Artificial Recharge 6.0 Ground Water related issue and problems 20 7.0 Mass Awareness and Training Activity 20 8.0 Area Notified by CGWB/SGWA 20 9.0 Recommendations 20 FIGURES 1.0 Index map of West Champaran district 2.0 Month wise rainfall plot for the district 3.0 Hydrogeological map of West Champaran district 4.0 Aquifer disposition in West Champaran 5.0 Depth to Water Level map (May 2011) 6.0 Depth to Water Level map (November 2011) 7.0 Block wise Dynamic Ground Water (GW) Resource of West Champaran district TABLES 1.0 Boundary details of West Champaran district 2.0 List of Blocks in West Champaran district 3.0 Land use pattern in West Champaran district 4.0 HNS locations of West Champaran 5.0 Blockwise Dynamic Ground Water Resource of West Champaran District (2008-09) 6.0 Exploration data of West Champaran 7.0 Chemical parameters of ground water in West Champaran 3 WEST CHAMPARAN - AT A GLANCE 1.
    [Show full text]
  • Sri Rama Navami
    Sri Rama Navami On Chaitra Sukla Navami (the ninth day of the bright half of Chaitra) 'Sree Ramanavami' is celebrated. Sree Rama was born on this day and years later on the same day Rama married Sita. 'Sree Sitarama Kalyana Mahotsav' (wedding) is performed in the abode Sitarama Temple, Bhadrachalam, Khammam District, Andhra Pradesh with great tradition and Bhakti. On behalf of Andhra Pradesh Government, Chief Minister with his wife visits the Kalyana Mahotsav and offers Silk Clothes and Pearls as Talambralu (auspicious) to the God and Goddess. The whole of this celebration is telecasted live in Doordarshan. "Wherever four Hindus live, Rama and Sita will be there" so said Swami Vivekananda, one of the foremost harbingers of modern national renaissance of Bharat. The reverse also is equally true - wherever Rama and Sita live, the people there will remain and live as Hindus. Every hill and rivulet of Bharat bears the imprint of the holy feet of Rama and Sita. Sri Rama reigns supreme to this day in the hearts of our people, cutting across all barriers of province, language, caste or sect. Even the tribes living in isolated valleys and jungles have names like Mitti-Ram and Patthar-Ram. In some other tribes, every name carries the proud suffix of Ram, such as Lutthu Ram, Jagadev Ram, etc. In many northern parts of Bharat mutual greetings take the form of Jay Ramjee Ki. Sri Rama has become so much identified with all the good and great and virile qualities of heroic manhood that expressions such as 'Us me Ram nahi hai' (there is no Rama in him) - meaning that a person has lost all manliness and worth - have become common usage.
    [Show full text]
  • Sch Code School Name Dist Name 11001 Zila School
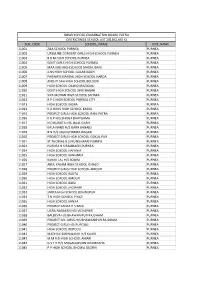
    BIHAR SCHOOL EXAMINATION BOARD PATNA DISTRICTWISE SCHOOL LIST 2013(CLASS X) SCH_CODE SCHOOL_NAME DIST_NAME 11001 ZILA SCHOOL PURNEA PURNEA 11002 URSULINE CONVENT GIRLS HIGH SCHOOL PURNEA PURNEA 11003 B B M HIGH SCHOOL PURNEA PURNEA 11004 GOVT GIRLS HIGH SCHOOL PURNEA PURNEA 11005 MAA KALI HIGH SCHOOL MADHUBANI PURNEA 11006 JLNS HIGH SCHOOL GULAB BAGH PURNEA 11007 PARWATI MANDAL HIGH SCHOOL HARDA PURNEA 11008 ANCHIT SAH HIGH SCHOOL BELOURI PURNEA 11009 HIGH SCHOOL CHANDI RAZIGANJ PURNEA 11010 GOVT HIGH SCHOOL SHRI NAGAR PURNEA 11011 SIYA MOHAN HIGH SCHOOL SAHARA PURNEA 11012 R P C HIGH SCHOOL PURNEA CITY PURNEA 11013 HIGH SCHOOL KASBA PURNEA 11014 K D GIRLS HIGH SCHOOL KASBA PURNEA 11015 PROJECT GIRLS HIGH SCHOOL RANI PATRA PURNEA 11016 K G P H/S BHOGA BHATGAMA PURNEA 11017 N D RUNGTA H/S JALAL GARH PURNEA 11018 KALA NAND H/S GARH BANAILI PURNEA 11019 B N H/S JAGNICHAMPA NAGAR PURNEA 11020 PROJECT GIRLS HIGH SCHOOL GOKUL PUR PURNEA 11021 ST THOMAS H S MUNSHIBARI PURNEA PURNEA 11023 PURNEA H S RAMBAGH,PURNEA PURNEA 11024 HIGH SCHOOL HAFANIA PURNEA 11025 HIGH SCHOOL KANHARIA PURNEA 11026 KANAK LAL H/S SOURA PURNEA 11027 ABUL KALAM HIGH SCHOOL ICHALO PURNEA 11028 PROJECT GIRLS HIGH SCHOOL AMOUR PURNEA 11029 HIGH SCHOOL RAUTA PURNEA 11030 HIGH SCHOOL AMOUR PURNEA 11031 HIGH SCHOOL BAISI PURNEA 11032 HIGH SCHOOL JHOWARI PURNEA 11033 JANTA HIGH SCHOOL BISHNUPUR PURNEA 11034 T N HIGH SCHOOL PIYAZI PURNEA 11035 HIGH SCHOOL KANJIA PURNEA 11036 PROJECT KANYA H S BAISI PURNEA 11037 UGRA NARAYAN H/S VIDYAPURI PURNEA 11038 BALDEVA H/S BHAWANIPUR RAJDHAM
    [Show full text]
  • 1. Shree Kailash-Mansarovar Pilgrimage (16 Nights/17 Days)
    ç Karnali Excursion Kailash Yatra 2018 Karnali Excursions, Nepal Shree Kailash and Mansarovar Pilgrimage 2018 Please join with us for the journey of a lifetime to experience Satyam, Shivam and Sundaram....! 1 Karnali Excursion Kailash Yatra 2018 Table of Contents: Particular Page 1. Mount Kailash and Mansarovar Pilgrimage Map 5 2. Shree Kailash-Mansarovar Pilgrimage (16 nights/17 days) 6 - 7 3. Shree Kailash-Mansarovar Pilgrimage with Muktinath & Damodar Kunda Darshan (20 nights/21 days) 8 - 10 4. Shree Kailash-Mansarovar Pilgrimage with Janakpur, Valmiki Ashram, Chitwan, Lumbini and Muktinath (23 nights /24 days) 11 - 14 5. World-wide contact details of Karnali Excurisions 16 2 Karnali Excursion Kailash Yatra 2018 Aum Namah Shivaya! Holy Mt. Kailash is considered as an important pilgrimage destination as well as a power point where it is possible to gain inspiration and energy to transform oneself from this physical to a higher spiritual level. The custom of circumambulating mount Kailash is believed to purify the soul and cultivate in each pilgrim the ability to perceive the divinity. The experience is elevating and inspiring, and many pilgrims return to their homes with feelings of exaltation and spiritual inspiration. Karnali Excursions was one of the first tour agencies in Nepal to offer pilgrimages to Shree Kailash in 1993, when China opened its doors to tourism. Ever since, we have been providing a strong, well-organized and spiritually fulfilling experience for those who join with us for this holy piligrimage of a lifetime. 3 Karnali Excursion Kailash Yatra 2018 What we offer: • We teach yoga and pranayam, which help to acclimatize in high altitude.
    [Show full text]
  • Analytical Study of Hilbert Space and Algebra of Operators
    "Science Stays True Here" Journal of Mathematics and Statistical Science (ISSN 2411-2518, USA), Vol.6, issues 5, 182-186 | Science Signpost Publishing Analytical Study of Hilbert Space and Algebra of Operators U.K. Srivastava1, L.K. Roy2, Binod Prasad3, C.D. Pathak4, & Surendra Ray5 Department of Mathematics 1. R.S.S. College, Chochahan, P.O.:- Aniruddh Belsar, Dist.- Muzaffarpur – 844111, B.R.A. Bihar University, Muzaffarpur – 842001, Bihar, India. 2. T.P. Varma College, Narkatiaganj, West Champaran – 845455 , B.R.A. Bihar University, Muzaffarpur – 842001 , Bihar, India. 3. T.R.M. Campus, Birganj, Parsa, Nepal, Tribhuvan University, Nepal. 4. R.R.M. Campus, Janakpurdham, Nepal, Tribhuvan University, Nepal. 5. R.R.M. Campus, Janakpurdham, Nepal, Tribhuvan University, Nepal. E-mail: [email protected] Abstract This present paper deals with the study of Hilbert Space and Algebra of Operators. Here, we consider R as additive group of reals with discrete topology and several ways of constructing C* - algebras Canonically associated with R and π, The Universal representation of R on Hilbert Space H, it is proved in this paper that all C*- algebras homomorphism and representation will be * - preserving Keywords: Hilbert space, Tensor product, C* - tensor norms, C* - algebras, Normal and Binormal norms, W*- algebras. Introduction E.G. Effros (1) and Kothe (3,4) are the pioneer workers of the present area. In fact, the present work is the extension of work done by Halub, J.R. (2), Kumar et al. (5), Kumar et al. (6), Kumar et al. (7), Srivastava et al. (8), Srivastava et al. (9), Srivastava et al.
    [Show full text]