DOCSLIB.ORG

Lecture 12 - Analog Communication (II)

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Lecture 12 - Analog Communication (II) Lecture 12 - Analog Communication (II) James Barnes ([email protected]) Spring 2009 Colorado State University Dept of Electrical and Computer Engineering ECE423 – 1 / 12 Outline ● QAM: quadrature amplitude modulation ● SSB: single sideband ● Lab suggestions Reference: ● Tretter Chapters 5-8 (On e-reserve), ● Haykin, Communication Systems, Third Edition Colorado State University Dept of Electrical and Computer Engineering ECE423 – 2 / 12 QAM Basics ● QAM=”Quadrature Amplitude Modulation” ● QAM is both a generic term which encompasses AM, FM, DSB-SC, and SSB (”linear modulation techniques”) and a specific technique for sending two independent messages over one carrier. ● For AM and SSB with pilot signal, the receiver oscillator can be derived from s(t); for DSB-SC and SSB without pilot signal, the receiver oscillator must be independently created. Colorado State University Dept of Electrical and Computer Engineering ECE423 – 3 / 12 QAM Modulator/Demodulator ● A picture of QAM commonly used in analog communication is given below. There is an alternate picture which is more useful and common in DSP, which will be shown later. ● For this representation, using the othogonality of sin(.) and cos(.), it is straightforward to show that the outputs of the LPF blocks are proportional to x(t) and y(t) as shown in the figure. Colorado State University Dept of Electrical and Computer Engineering ECE423 – 4 / 12 Modulation Types ● For AM, x(t) = Ac[1 + kam(t)], y(t) = 0. ● For DSB-SC, x(t) = Acm(t), y(t) = 0. ● For SSB, x(t) = m(t), y(t) = m(ˆt). ● For QAM modulation, x(t) and y(t) can be independent signals, called in-phase and quadrature respectively. ● For FM, x(t) = cos(φ(t)), y(t) = sin(φ(t)). Colorado State University Dept of Electrical and Computer Engineering ECE423 – 5 / 12 Complex Baseband Representation of Passband Signals ● We can picture x(t) and y(t) as being real and imaginary components of a complex baseband signal z(t) = x(t) + jy(t). ● z(t) can be transformed into a real passband signal and vice-versa. This is modulation and de-modulation. ● With independent x(t) and y(t), the modulated passband signal will be similar to DSB-SC in bandwidth utilization, but we will send two independent channels in the same bandwidth. ● If x(t) and y(t) are not independent, but instead y(t) = ±xˆ(t), ˆ≡ Hilbert tranform, then we can send one channel in either the upper sideband or lower sideband only (SSB), thus using half the bandwidth of DSB-SC and power of DSB-SC. Colorado State University Dept of Electrical and Computer Engineering ECE423 – 6 / 12 Modulation of Complex Baseband Signal jωct ● Let w(t) = z(t)e , where ωc is the carrier frequency. We know from the Modulation Theorem that W (ω) = Z(ω − ωc). W has only a positive frequency component (is an ”analytic signal”) and spans a bandwidth of 2B, which is the bandwidth of z(t). ● We can form a real passband signal by converting w(t) to real: 1 s(t) = 2 [w(t) + w(t)], where w(t) is the complex conjugate of w(t). Can jωct −jωct easily show that s(t) = z(t)e + z(t)e = x(t)cos(ωct) − y(t)sin(ωct). Colorado State University Dept of Electrical and Computer Engineering ECE423 – 7 / 12 Demodulation of Complex Baseband Signal ● Assume the received signal is s(t) (no channel distortion). ● First put s(t) through a ”phase splitter” filter φ(t) ↔F T Φ(jω) = u(ω), where u(ω) is a frequency step function. The phase splitter discards the negative frequency term in s(t) and we recover w(t) = z(t)ejωct. ● Next multiply w(t) by a locally-generated complex exponential e−jωct to recover z(t). Colorado State University Dept of Electrical and Computer Engineering ECE423 – 8 / 12 Recovering Carrier We cannot regenerate the carrier using the quadrature component, as with the Costas receiver. There are two strategies for dealing with this: 1. Free-running at the carrier frequency, with some phase error (distortion). This is tolerable for many applications (voice). 2. Add small DC component to m(t) – ”pilot tone”. This requires that m(t) be passband (no DC component). Then s(t) = x(t)cos(ωct) − y(t)sin(ωct) + pcos(ωct). This produces a small carrier signal which can be locked onto by a PLL or amplified to create the ”local oscillator” signal. Colorado State University Dept of Electrical and Computer Engineering ECE423 – 9 / 12 SSB Modulation ● To achieve SSB, the only difference is that we generate the complex baseband signal from a real baseband signal m(t) by passing through a phase splitter. This creates an analytic signal z(t) = m(t) ± jmˆ(t) which has only positive or negative frequency components. This is the positive or negative pre-envelope. When multiplied by ejωct and converted to real, s(t) will have only upper or lower sideband components, depending on the sign in z(t). ● De-modulation in principle is the same as before. Colorado State University Dept of Electrical and Computer Engineering ECE423 – 10 / 12 Practical: Creating a Phase Splitter ● Remember that H(jω) = −jsgn(ω) is the Hilbert Transform. There are cof files for various orders of Hilbert Transformers in the lab support files. ● How do you multiply by j? 1 r(t) = s(t) + w(t) = s(t) + jdž(t) -j sgn(Z) j Phase Splitter: )( jZ) Colorado State University Dept of Electrical and Computer Engineering ECE423 – 11 / 12 Practical: QAM Receiver using Pilot Tone Re[·] BPF DAC x(t) received signal x -j sgn(Ȧ) nto Hilbert Transformer Im[·] BPF DAC y(t) 1 r Baseband Filters 1 2 2 That Remove DC 1 2rcos(Zcto )z r z Components In-phase Carrier 1 1 r cos(Zcto )z Quadrature Carrier 1 rsin(Zcto )z Bandpass Carrier Recovery Filters Colorado State University Dept of Electrical and Computer Engineering ECE423 – 12 / 12.
Load more

Recommended publications
  • Optical Single Sideband for Broadband and Subcarrier Systems
    University of Alberta Optical Single Sideband for Broadband And Subcarrier Systems Robert James Davies 0 A thesis submitted to the faculty of Graduate Studies and Research in partial fulfillrnent of the requirernents for the degree of Doctor of Philosophy Department of Electrical And Computer Engineering Edmonton, AIberta Spring 1999 National Library Bibliothèque nationale du Canada Acquisitions and Acquisitions et Bibliographie Services services bibliographiques 395 Wellington Street 395, rue Wellington Ottawa ON KlA ON4 Ottawa ON KIA ON4 Canada Canada Yom iUe Votre relérence Our iSie Norre reference The author has granted a non- L'auteur a accordé une licence non exclusive licence allowing the exclusive permettant à la National Library of Canada to Bibliothèque nationale du Canada de reproduce, loan, distribute or sell reproduire, prêter, distribuer ou copies of this thesis in microform, vendre des copies de cette thèse sous paper or electronic formats. la forme de microfiche/nlm, de reproduction sur papier ou sur format électronique. The author retains ownership of the L'auteur conserve la propriété du copyright in this thesis. Neither the droit d'auteur qui protège cette thèse. thesis nor substantial extracts fkom it Ni la thèse ni des extraits substantiels may be printed or otheMrise de celle-ci ne doivent être Unprimés reproduced without the author's ou autrement reproduits sans son permission. autorisation. Abstract Radio systems are being deployed for broadband residential telecommunication services such as broadcast, wideband lntemet and video on demand. Justification for radio delivery centers on mitigation of problems inherent in subscriber loop upgrades such as Fiber to the Home (WH)and Hybrid Fiber Coax (HFC).
    [Show full text]
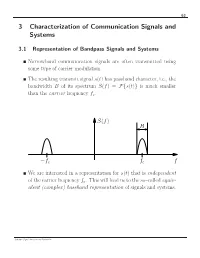
  • 3 Characterization of Communication Signals and Systems
    63 3 Characterization of Communication Signals and Systems 3.1 Representation of Bandpass Signals and Systems Narrowband communication signals are often transmitted using some type of carrier modulation. The resulting transmit signal s(t) has passband character, i.e., the bandwidth B of its spectrum S(f) = s(t) is much smaller F{ } than the carrier frequency fc. S(f) B f f f − c c We are interested in a representation for s(t) that is independent of the carrier frequency fc. This will lead us to the so–called equiv- alent (complex) baseband representation of signals and systems. Schober: Signal Detection and Estimation 64 3.1.1 Equivalent Complex Baseband Representation of Band- pass Signals Given: Real–valued bandpass signal s(t) with spectrum S(f) = s(t) F{ } Analytic Signal s+(t) In our quest to find the equivalent baseband representation of s(t), we first suppress all negative frequencies in S(f), since S(f) = S( f) is valid. − The spectrum S+(f) of the resulting so–called analytic signal s+(t) is defined as S (f) = s (t) =2 u(f)S(f), + F{ + } where u(f) is the unit step function 0, f < 0 u(f) = 1/2, f =0 . 1, f > 0 u(f) 1 1/2 f Schober: Signal Detection and Estimation 65 The analytic signal can be expressed as 1 s+(t) = − S+(f) F 1{ } = − 2 u(f)S(f) F 1{ } 1 = − 2 u(f) − S(f) F { } ∗ F { } 1 The inverse Fourier transform of − 2 u(f) is given by F { } 1 j − 2 u(f) = δ(t) + .
    [Show full text]
  • Design and Application of a Hilbert Transformer in a Digital Receiver
    Proceedings of the SDR 11 Technical Conference and Product Exposition, Copyright © 2011 Wireless Innovation Forum All Rights Reserved DESIGN AND APPLICATION OF A HILBERT TRANSFORMER IN A DIGITAL RECEIVER Matt Carrick (Northrop Grumman, Chantilly, VA, USA; [email protected]); Doug Jaeger (Northrop Grumman, Chantilly, VA, USA; [email protected]); fred harris (San Diego State University, San Diego, CA, USA; [email protected]) ABSTRACT A common method of down converting a signal from an intermediate frequency (IF) to baseband is using a quadrature down-converter. One problem with the quadrature down-converter is it requires two low pass filters; one for the real branch and one for the imaginary branch. A more efficient way is to transform the real signal to a complex signal and then complex heterodyne the resultant signal to baseband. The transformation of a real signal to a complex signal can be done using a Hilbert transform. Building a Hilbert transform directly from its sampled data sequence produces suboptimal results due to time series truncation; another method is building a Hilbert transformer by synthesizing the filter coefficients from half Figure 1: A quadrature down-converter band filter coefficients. Designing the Hilbert transform filter using a half band filter allows for a much more Another way of viewing the problem is that the structured design process as well as greatly improved quadrature down-converter not only extracts the desired results. segment of the spectrum it rejects the undesired spectral image, the spectral replica present in the Hermetian 1. INTRODUCTION symmetric spectra of a real signal. Removing this image would result in a single sided spectrum which being non- The digital portion of a receiver is typically designed to Hermetian symmetric is the transform of a complex signal.
    [Show full text]
  • 2 the Wireless Channel
    CHAPTER 2 The wireless channel A good understanding of the wireless channel, its key physical parameters and the modeling issues, lays the foundation for the rest of the book. This is the goal of this chapter. A defining characteristic of the mobile wireless channel is the variations of the channel strength over time and over frequency. The variations can be roughly divided into two types (Figure 2.1): • Large-scale fading, due to path loss of signal as a function of distance and shadowing by large objects such as buildings and hills. This occurs as the mobile moves through a distance of the order of the cell size, and is typically frequency independent. • Small-scale fading, due to the constructive and destructive interference of the multiple signal paths between the transmitter and receiver. This occurs at the spatialscaleoftheorderofthecarrierwavelength,andisfrequencydependent. We will talk about both types of fading in this chapter, but with more emphasis on the latter. Large-scale fading is more relevant to issues such as cell-site planning. Small-scale multipath fading is more relevant to the design of reliable and efficient communication systems – the focus of this book. We start with the physical modeling of the wireless channel in terms of elec- tromagnetic waves. We then derive an input/output linear time-varying model for the channel, and define some important physical parameters. Finally, we introduce a few statistical models of the channel variation over time and over frequency. 2.1 Physical modeling for wireless channels Wireless channels operate through electromagnetic radiation from the trans- mitter to the receiver.
    [Show full text]
  • An FPGA-BASED Implementation of a Hilbert Filter for Real-Time Estimation of Instantaneous Frequency, Phase and Amplitude of Power System Signals
    International Journal of Applied Engineering Research ISSN 0973-4562 Volume 13, Number 23 (2018) pp. 16333-16341 © Research India Publications. http://www.ripublication.com An FPGA-BASED implementation of a Hilbert filter for Real-time Estimation of Instantaneous Frequency, Phase and Amplitude of Power System Signals Q. Bart and R. Tzoneva Department of Electrical, Electronic and Computer Engineering, Cape Peninsula University of Technology, Cape town, 7535, South Africa. Abstract apriori knowledge for a particular fixed sampling rate. The DFT is periodic in nature and assumes that the window of The instantaneous parameters, amplitude, phase and sampled data contains an integer number of waveform cycles. frequency of power system signals provide valuable During frequency perturbations the sampled data may not information about the status of the power system, particularly comprise an integer number of cycles resulting in when these parameters can be obtained simultaneously from discontinuities at the endpoints. This is one of the locations that are remotely located from each other. Phasor disadvantages of the DFT for real-time estimation of Measurement Units (PMU’s) placed at these remote locations synchrophasors and this phenomenon is commonly known as can perform these simultaneous time synchronized spectral leakage. In order to accommodate the dynamic measurements. In this work digital signal processing nature of power system signals an extension of the DFT techniques and Field Programmable Gate Array (FPGA) known as the Taylor-Fourier Transform [4],[5] has also been technology was used for the real-time estimation of power utilized as a synchrophasor estimator. Alternative techniques system signal parameters. These parameters were estimated such as Kalman Filtering [6] and Enhanced Phase Locked based upon an approach utilizing the Hilbert transform and Loop techniques [7] have also been proposed.
    [Show full text]
  • Arxiv:1611.05269V3 [Cs.IT] 29 Jan 2018 Graph Analytic Signal, and Associated Amplitude and Frequency Modulations Reveal Com
    On Hilbert Transform, Analytic Signal, and Modulation Analysis for Signals over Graphs Arun Venkitaraman, Saikat Chatterjee, Peter Handel¨ Department of Information Science and Engineering, School of Electrical Engineering and ACCESS Linnaeus Center KTH Royal Institute of Technology, SE-100 44 Stockholm, Sweden . Abstract We propose Hilbert transform and analytic signal construction for signals over graphs. This is motivated by the popularity of Hilbert transform, analytic signal, and mod- ulation analysis in conventional signal processing, and the observation that comple- mentary insight is often obtained by viewing conventional signals in the graph setting. Our definitions of Hilbert transform and analytic signal use a conjugate-symmetry-like property exhibited by the graph Fourier transform (GFT), resulting in a ’one-sided’ spectrum for the graph analytic signal. The resulting graph Hilbert transform is shown to possess many interesting mathematical properties and also exhibit the ability to high- light anomalies/discontinuities in the graph signal and the nodes across which signal discontinuities occur. Using the graph analytic signal, we further define amplitude, phase, and frequency modulations for a graph signal. We illustrate the proposed con- cepts by showing applications to synthesized and real-world signals. For example, we show that the graph Hilbert transform can indicate presence of anomalies and that arXiv:1611.05269v3 [cs.IT] 29 Jan 2018 graph analytic signal, and associated amplitude and frequency modulations reveal com- plementary information in speech signals. Keywords: Graph signal, analytic signal, Hilbert transform, demodulation, anomaly detection. Email addresses: [email protected] (Arun Venkitaraman), [email protected] (Saikat Chatterjee), [email protected] (Peter Handel)¨ Preprint submitted to Signal Processing 1 1 0.8 0.8 0.6 0.6 0.4 0.4 0.2 0.2 0 0 (a) (b) Figure 1: Anomaly highlighting behavior of the graph Hilbert transform for 2D image signal graph.
    [Show full text]
  • 7.3.7 Video Cassette Recorders (VCR) 7.3.8 Video Disk Recorders
    /7 7.3.5 Fiber-Optic Cables (FO) 7.3.6 Telephone Company Unes (TELCO) 7.3.7 Video Cassette Recorders (VCR) 7.3.8 Video Disk Recorders 7.4 Transmission Security 8. Consumer Equipment Issues 8.1 Complexity of Receivers 8.2 Receiver Input/Output Characteristics 8.2.1 RF Interface 8.2.2 Baseband Video Interface 8.2.3 Baseband Audio Interface 8.2.4 Interfacing with Ancillary Signals 8.2.5 Receiver Antenna Systems Requirements 8.3 Compatibility with Existing NTSC Consumer Equipment 8.3.1 RF Compatibility 8.3.2 Baseband Video Compatibility 8.3.3 Baseband Audio Compatibility 8.3.4 IDTV Receiver Compatibility 8.4 Allows Multi-Standard Display Devices 9. Other Considerations 9.1 Practicality of Near-Term Technological Implementation 9.2 Long-Term Viability/Rate of Obsolescence 9.3 Upgradability/Extendability 9.4 Studio/Plant Compatibility Section B: EXPLANATORY NOTES OF ATTRIBUTES/SYSTEMS MATRIX Items on the Attributes/System Matrix for which no explanatory note is provided were deemed to be self-explanatory. I. General Description (Proponent) section I shall be used by a system proponent to define the features of the system being proposed. The features shall be defined and organized under the headings ot the following subsections 1 through 4. section I. General Description (Proponent) shall consist of a description of the proponent system in narrative form, which covers all of the features and characteris­ tics of the system which the proponent wishe. to be included in the public record, and which will be used by various groups to analyze and understand the system proposed, and to compare with other propo.ed systems.
    [Show full text]
  • Baseband Harmonic Distortions in Single Sideband Transmitter and Receiver System
    Baseband Harmonic Distortions in Single Sideband Transmitter and Receiver System Kang Hsia Abstract: Telecommunications industry has widely adopted single sideband (SSB or complex quadrature) transmitter and receiver system, and one popular implementation for SSB system is to achieve image rejection through quadrature component image cancellation. Typically, during the SSB system characterization, the baseband fundamental tone and also the harmonic distortion products are important parameters besides image and LO feedthrough leakage. To ensure accurate characterization, the actual frequency locations of the harmonic distortion products are critical. While system designers may be tempted to assume that the harmonic distortion products are simply up-converted in the same fashion as the baseband fundamental frequency component, the actual distortion products may have surprising results and show up on the different side of spectrum. This paper discusses the theory of SSB system and the actual location of the baseband harmonic distortion products. Introduction Communications engineers have utilized SSB transmitter and receiver system because it offers better bandwidth utilization than double sideband (DSB) transmitter system. The primary cause of bandwidth overhead for the double sideband system is due to the image component during the mixing process. Given data transmission bandwidth of B, the former requires minimum bandwidth of B whereas the latter requires minimum bandwidth of 2B. While the filtering of the image component is one type of SSB implementation, another type of SSB system is to create a quadrature component of the signal and ideally cancels out the image through phase cancellation. M(t) M(t) COS(2πFct) Baseband Message Signal (BB) Modulated Signal (RF) COS(2πFct) Local Oscillator (LO) Signal Figure 1.
    [Show full text]
  • Baseband Video Testing with Digital Phosphor Oscilloscopes
    Application Note Baseband Video Testing With Digital Phosphor Oscilloscopes Video signals are complex pose instrument that can pro- This application note demon- waveforms comprised of sig- vide accurate information – strates the use of a Tektronix nals representing a picture as quickly and easily. Finally, to TDS 700D-series Digital well as the timing informa- display all of the video wave- Phosphor Oscilloscope to tion needed to display the form details, a fast acquisi- make a variety of common picture. To capture and mea- tion technology teamed with baseband video measure- sure these complex signals, an intensity-graded display ments and examines some of you need powerful instru- give the confidence and the critical measurement ments tailored for this appli- insight needed to detect and issues. cation. But, because of the diagnose problems with the variety of video standards, signal. you also need a general-pur- Copyright © 1998 Tektronix, Inc. All rights reserved. Video Basics Video signals come from a for SMPTE systems, etc. The active portion of the video number of sources, including three derived component sig- signal. Finally, the synchro- cameras, scanners, and nals can then be distributed nization information is graphics terminals. Typically, for processing. added. Although complex, the baseband video signal Processing this composite signal is a sin- begins as three component gle signal that can be carried analog or digital signals rep- In the processing stage, video on a single coaxial cable. resenting the three primary component signals may be combined to form a single Component Video Signals. color elements – the Red, Component signals have an Green, and Blue (RGB) com- composite video signal (as in NTSC or PAL systems), advantage of simplicity in ponent signals.
    [Show full text]
  • Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation
    Digital Baseband Modulation Outline • Later Baseband & Bandpass Waveforms Baseband & Bandpass Waveforms, Modulation A Communication System Dig. Baseband Modulators (Line Coders) • Sequence of bits are modulated into waveforms before transmission • à Digital transmission system consists of: • The modulator is based on: • The symbol mapper takes bits and converts them into symbols an) – this is done based on a given table • Pulse Shaping Filter generates the Gaussian pulse or waveform ready to be transmitted (Baseband signal) Waveform; Sampled at T Pulse Amplitude Modulation (PAM) Example: Binary PAM Example: Quaternary PAN PAM Randomness • Since the amplitude level is uniquely determined by k bits of random data it represents, the pulse amplitude during the nth symbol interval (an) is a discrete random variable • s(t) is a random process because pulse amplitudes {an} are discrete random variables assuming values from the set AM • The bit period Tb is the time required to send a single data bit • Rb = 1/ Tb is the equivalent bit rate of the system PAM T= Symbol period D= Symbol or pulse rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate • If quaternary signaling & pulse rate is 9600 find bit rate Example • Amplitude pulse modulation • If binary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 • If quaternary signaling & pulse rate is 9600 find bit rate M=2à k=1à bite rate Rb=1/Tb=k.D = 9600 Binary Line Coding Techniques • Line coding - Mapping of binary information sequence into the digital signal that enters the baseband channel • Symbol mapping – Unipolar - Binary 1 is represented by +A volts pulse and binary 0 by no pulse during a bit period – Polar - Binary 1 is represented by +A volts pulse and binary 0 by –A volts pulse.
    [Show full text]
  • FM Stereo Format 1
    A brief history • 1931 – Alan Blumlein, working for EMI in London patents the stereo recording technique, using a figure-eight miking arrangement. • 1933 – Armstrong demonstrates FM transmission to RCA • 1935 – Armstrong begins 50kW experimental FM station at Alpine, NJ • 1939 – GE inaugurates FM broadcasting in Schenectady, NY – TV demonstrations held at World’s Fair in New York and Golden Gate Interna- tional Exhibition in San Francisco – Roosevelt becomes first U.S. president to give a speech on television – DuMont company begins producing television sets for consumers • 1942 – Digital computer conceived • 1945 – FM broadcast band moved to 88-108MHz • 1947 – First taped US radio network program airs, featuring Bing Crosby – 3M introduces Scotch 100 audio tape – Transistor effect demonstrated at Bell Labs • 1950 – Stereo tape recorder, Magnecord 1250, introduced • 1953 – Wireless microphone demonstrated – AM transmitter remote control authorized by FCC – 405-line color system developed by CBS with ”crispening circuits” to improve apparent picture resolution 1 – FCC reverses its decision to approve the CBS color system, deciding instead to authorize use of the color-compatible system developed by NTSC – Color TV broadcasting begins • 1955 – Computer hard disk introduced • 1957 – Laser developed • 1959 – National Stereophonic Radio Committee formed to decide on an FM stereo system • 1960 – Stereo FM tests conducted over KDKA-FM Pittsburgh • 1961 – Great Rose Bowl Hoax University of Washington vs. Minnesota (17-7) – Chevrolet Impala ‘Super Sport’ Convertible with 409 cubic inch V8 built – FM stereo transmission system approved by FCC – First live televised presidential news conference (John Kennedy) • 1962 – Philips introduces audio cassette tape player – The Beatles release their first UK single Love Me Do/P.S.
    [Show full text]
  • An Analysis of a Quadrature Double-Sideband/Frequency Modulated Communication System
    Scholars' Mine Masters Theses Student Theses and Dissertations 1970 An analysis of a quadrature double-sideband/frequency modulated communication system Denny Ray Townson Follow this and additional works at: https://scholarsmine.mst.edu/masters_theses Part of the Electrical and Computer Engineering Commons Department: Recommended Citation Townson, Denny Ray, "An analysis of a quadrature double-sideband/frequency modulated communication system" (1970). Masters Theses. 7225. https://scholarsmine.mst.edu/masters_theses/7225 This thesis is brought to you by Scholars' Mine, a service of the Missouri S&T Library and Learning Resources. This work is protected by U. S. Copyright Law. Unauthorized use including reproduction for redistribution requires the permission of the copyright holder. For more information, please contact [email protected]. AN ANALYSIS OF A QUADRATURE DOUBLE- SIDEBAND/FREQUENCY MODULATED COMMUNICATION SYSTEM BY DENNY RAY TOWNSON, 1947- A THESIS Presented to the Faculty of the Graduate School of the UNIVERSITY OF MISSOURI - ROLLA In Partial Fulfillment of the Requirements for the Degree MASTER OF SCIENCE IN ELECTRICAL ENGINEERING 1970 ii ABSTRACT A QDSB/FM communication system is analyzed with emphasis placed on the QDSB demodulation process and the AGC action in the FM transmitter. The effect of noise in both the pilot and message signals is investigated. The detection gain and mean square error is calculated for the QDSB baseband demodulation process. The mean square error is also evaluated for the QDSB/FM system. The AGC circuit is simulated on a digital computer. Errors introduced into the AGC system are analyzed with emphasis placed on nonlinear gain functions for the voltage con­ trolled amplifier.
    [Show full text]