Readingsample
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

LCROSS (Lunar Crater Observation and Sensing Satellite) Observation Campaign: Strategies, Implementation, and Lessons Learned
Space Sci Rev DOI 10.1007/s11214-011-9759-y LCROSS (Lunar Crater Observation and Sensing Satellite) Observation Campaign: Strategies, Implementation, and Lessons Learned Jennifer L. Heldmann · Anthony Colaprete · Diane H. Wooden · Robert F. Ackermann · David D. Acton · Peter R. Backus · Vanessa Bailey · Jesse G. Ball · William C. Barott · Samantha K. Blair · Marc W. Buie · Shawn Callahan · Nancy J. Chanover · Young-Jun Choi · Al Conrad · Dolores M. Coulson · Kirk B. Crawford · Russell DeHart · Imke de Pater · Michael Disanti · James R. Forster · Reiko Furusho · Tetsuharu Fuse · Tom Geballe · J. Duane Gibson · David Goldstein · Stephen A. Gregory · David J. Gutierrez · Ryan T. Hamilton · Taiga Hamura · David E. Harker · Gerry R. Harp · Junichi Haruyama · Morag Hastie · Yutaka Hayano · Phillip Hinz · Peng K. Hong · Steven P. James · Toshihiko Kadono · Hideyo Kawakita · Michael S. Kelley · Daryl L. Kim · Kosuke Kurosawa · Duk-Hang Lee · Michael Long · Paul G. Lucey · Keith Marach · Anthony C. Matulonis · Richard M. McDermid · Russet McMillan · Charles Miller · Hong-Kyu Moon · Ryosuke Nakamura · Hirotomo Noda · Natsuko Okamura · Lawrence Ong · Dallan Porter · Jeffery J. Puschell · John T. Rayner · J. Jedadiah Rembold · Katherine C. Roth · Richard J. Rudy · Ray W. Russell · Eileen V. Ryan · William H. Ryan · Tomohiko Sekiguchi · Yasuhito Sekine · Mark A. Skinner · Mitsuru Sôma · Andrew W. Stephens · Alex Storrs · Robert M. Suggs · Seiji Sugita · Eon-Chang Sung · Naruhisa Takatoh · Jill C. Tarter · Scott M. Taylor · Hiroshi Terada · Chadwick J. Trujillo · Vidhya Vaitheeswaran · Faith Vilas · Brian D. Walls · Jun-ihi Watanabe · William J. Welch · Charles E. Woodward · Hong-Suh Yim · Eliot F. Young Received: 9 October 2010 / Accepted: 8 February 2011 © The Author(s) 2011. -

Martian Crater Morphology
ANALYSIS OF THE DEPTH-DIAMETER RELATIONSHIP OF MARTIAN CRATERS A Capstone Experience Thesis Presented by Jared Howenstine Completion Date: May 2006 Approved By: Professor M. Darby Dyar, Astronomy Professor Christopher Condit, Geology Professor Judith Young, Astronomy Abstract Title: Analysis of the Depth-Diameter Relationship of Martian Craters Author: Jared Howenstine, Astronomy Approved By: Judith Young, Astronomy Approved By: M. Darby Dyar, Astronomy Approved By: Christopher Condit, Geology CE Type: Departmental Honors Project Using a gridded version of maritan topography with the computer program Gridview, this project studied the depth-diameter relationship of martian impact craters. The work encompasses 361 profiles of impacts with diameters larger than 15 kilometers and is a continuation of work that was started at the Lunar and Planetary Institute in Houston, Texas under the guidance of Dr. Walter S. Keifer. Using the most ‘pristine,’ or deepest craters in the data a depth-diameter relationship was determined: d = 0.610D 0.327 , where d is the depth of the crater and D is the diameter of the crater, both in kilometers. This relationship can then be used to estimate the theoretical depth of any impact radius, and therefore can be used to estimate the pristine shape of the crater. With a depth-diameter ratio for a particular crater, the measured depth can then be compared to this theoretical value and an estimate of the amount of material within the crater, or fill, can then be calculated. The data includes 140 named impact craters, 3 basins, and 218 other impacts. The named data encompasses all named impact structures of greater than 100 kilometers in diameter. -

March 21–25, 2016
FORTY-SEVENTH LUNAR AND PLANETARY SCIENCE CONFERENCE PROGRAM OF TECHNICAL SESSIONS MARCH 21–25, 2016 The Woodlands Waterway Marriott Hotel and Convention Center The Woodlands, Texas INSTITUTIONAL SUPPORT Universities Space Research Association Lunar and Planetary Institute National Aeronautics and Space Administration CONFERENCE CO-CHAIRS Stephen Mackwell, Lunar and Planetary Institute Eileen Stansbery, NASA Johnson Space Center PROGRAM COMMITTEE CHAIRS David Draper, NASA Johnson Space Center Walter Kiefer, Lunar and Planetary Institute PROGRAM COMMITTEE P. Doug Archer, NASA Johnson Space Center Nicolas LeCorvec, Lunar and Planetary Institute Katherine Bermingham, University of Maryland Yo Matsubara, Smithsonian Institute Janice Bishop, SETI and NASA Ames Research Center Francis McCubbin, NASA Johnson Space Center Jeremy Boyce, University of California, Los Angeles Andrew Needham, Carnegie Institution of Washington Lisa Danielson, NASA Johnson Space Center Lan-Anh Nguyen, NASA Johnson Space Center Deepak Dhingra, University of Idaho Paul Niles, NASA Johnson Space Center Stephen Elardo, Carnegie Institution of Washington Dorothy Oehler, NASA Johnson Space Center Marc Fries, NASA Johnson Space Center D. Alex Patthoff, Jet Propulsion Laboratory Cyrena Goodrich, Lunar and Planetary Institute Elizabeth Rampe, Aerodyne Industries, Jacobs JETS at John Gruener, NASA Johnson Space Center NASA Johnson Space Center Justin Hagerty, U.S. Geological Survey Carol Raymond, Jet Propulsion Laboratory Lindsay Hays, Jet Propulsion Laboratory Paul Schenk, -

Weekly Bulletin for Period 08/05/2018 - 08/11/2018
OFFICE OF THE COMPTROLLER OF THE CURRENCY WEEKLY BULLETIN FOR PERIOD 08/05/2018 - 08/11/2018 The absence of a comment period end date indicates the comment period has expired or a comment period is not applicable. Comments may still be submitted to OCC even after the comment period ends. Please refer to the Public Notice and Comment booklet by clicking here: Click here for booklet Also, searches on any application filed with the OCC can be made using the Corporate Applications Search (CAS) tool by clicking here: Click here for CAS ACTION DATE TYPE APPLICATION BANK NAME BRANCH NAME LOCATION CITY STATE COUNTY CMT PD END NUMBER TARGET BANK Details RECEIPT 8/7/2018 5.53 SUBSTANTIAL 2018-LB-5.53-304592 WELLS FARGO N/A 4455 SPRING LAS VEGAS NV CLARK COUNTY CHANGE IN FINANCIAL NB MOUNTAIN ASSETS ROAD Details CONSUMMATED 8/10/2018 BRANCH 2018-CE- FIRST MID- FIRST MID- 2229 SOUTH CHAMPAIGN IL CHAMPAIGN EFFECTIVE CLOSINGS BRANCHCLOSING- ILLINOIS BANK & ILLINOIS BANK & NEIL STREET COUNTY 302485 TRUST, NA TRUST BRANCH Details CONSUMMATED 8/10/2018 BRANCH 2018-CE- U.S. BANK NA FORT UNION UT 800 FORT UNION MIDVALE UT SALT LAKE EFFECTIVE CLOSINGS BRANCHCLOSING- BRANCH BOULEVARD COUNTY 303187 Details CONSUMMATED 8/10/2018 BRANCH 2018-CE- U.S. BANK NA NORTHEDGE NORTH BARRON EATON OH PREBLE COUNTY EFFECTIVE CLOSINGS BRANCHCLOSING- OFFICE STREET 303188 Details RECEIPT 8/6/2018 BRANCH 2018-CE- FORCHT BANK, FAIRDALE 10706 WEST FAIRDALE KY LOUISVILLE CLOSINGS BRANCHCLOSING- NATIONAL BANKING CENTER MANSLICK JEFFERSON 304554 ASSOCIATION ROAD COUNTY METRO GOVERNMENT ACTION DATE TYPE APPLICATION BANK NAME BRANCH NAME LOCATION CITY STATE COUNTY CMT PD END NUMBER TARGET BANK Details RECEIPT 8/6/2018 BRANCH 2018-CE- FORCHT BANK, NOT GIVEN FIRST WHITLEY CITY KY MCCREARY CLOSINGS BRANCHCLOSING- NATIONAL FINANCIAL COUNTY 304556 ASSOCIATION PLAZA Details RECEIPT 8/6/2018 BRANCH 2018-CE- FORCHT BANK, CORINTH HIGHWAY 330 CORINTH KY GRANT COUNTY CLOSINGS BRANCHCLOSING- NATIONAL AND I-75 304557 ASSOCIATION INTERCHANGE Details RECEIPT 8/7/2018 BRANCH 2018-CE- U.S. -

Complex Explosive Volcanic Activity on the Moon Within Oppenheimer Crater
Icarus 273 (2016) 296–314 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Complex explosive volcanic activity on the Moon within Oppenheimer crater ∗ Kristen A. Bennett a, ,BrionyH.N. Horgan b, Lisa R. Gaddis c, Benjamin T. Greenhagen d, Carlton C. Allen e,PaulO. Hayne f, James F. Bell III a, David A. Paige g a School of Earth and Space Exploration, Arizona State University. ISTB4 Room 795, 781 Terrace Mall, Tempe AZ 85287, United States b Department of Earth, Atmospheric, and Planetary Sciences, Purdue University, 550 Stadium Mall Drive, West Lafayette, IN 47907, United States c Astrogeology Science Center, U.S. Geological Survey, 2255 N. Gemini Drive, Flagstaff, AZ 86001, United States d Johns Hopkins University Applied Physics Laboratory, 11100 Johns Hopkins Rd, Laurel, MD 20723, United States e NASA Johnson Space Center, Emeritus, 2101 NASA Road 1, Houston, TX 77058, United States f NASA Jet Propulsion Laboratory, 4800 Oak Grove Dr, Pasadena, CA 91109, United States g Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles, 595 Charles E Young Dr E, Los Angeles, CA 90095, United States a r t i c l e i n f o a b s t r a c t Article history: Oppenheimer crater is a floor-fractured crater located within the South Pole–Aitken basin on the Moon, Received 27 July 2015 and exhibits more than a dozen localized pyroclastic deposits associated with the fractures. Localized Revised 10 December 2015 pyroclastic volcanism on the Moon is thought to form as a result of intermittently explosive Vulcanian Accepted 3 February 2016 eruptions under low effusion rates, in contrast to the higher-effusion rate, Hawaiian-style fire fountaining Available online 10 February 2016 inferred to form larger regional deposits. -

Geologic Studies of Planetary Surfaces Using Radar Polarimetric Imaging 2
Geologic studies of planetary surfaces using radar polarimetric imaging 2 4 Lynn M. Carter NASA Goddard Space Flight Center 8 Donald B. Campbell 9 Cornell University 10 11 Bruce A. Campbell 12 Smithsonian Institution 13 14 14 Abstract: Radar is a useful remote sensing tool for studying planetary geology because it is 15 sensitive to the composition, structure, and roughness of the surface and can penetrate some 16 materials to reveal buried terrain. The Arecibo Observatory radar system transmits a single 17 sense of circular polarization, and both senses of circular polarization are received, which allows 18 for the construction of the Stokes polarization vector. From the Stokes vector, daughter products 19 such as the circular polarization ratio, the degree of linear polarization, and linear polarization 20 angle are obtained. Recent polarimetric imaging using Arecibo has included Venus and the 21 Moon. These observations can be compared to radar data for terrestrial surfaces to better 22 understand surface physical properties and regional geologic evolution. For example, 23 polarimetric radar studies of volcanic settings on Venus, the Moon and Earth display some 24 similarities, but also illustrate a variety of different emplacement and erosion mechanisms. 25 Polarimetric radar data provides important information about surface properties beyond what can 26 be obtained from single-polarization radar. Future observations using polarimetric synthetic 27 aperture radar will provide information on roughness, composition and stratigraphy that will 28 support a broader interpretation of surface evolution. 29 2 29 1.0 Introduction 30 31 Radar polarimetry has the potential to provide more information about surface physical 32 properties than single-polarization backscatter measurements, and has often been used in remote 33 sensing observations of Solar System objects. -

South Pole-Aitken Basin
Feasibility Assessment of All Science Concepts within South Pole-Aitken Basin INTRODUCTION While most of the NRC 2007 Science Concepts can be investigated across the Moon, this chapter will focus on specifically how they can be addressed in the South Pole-Aitken Basin (SPA). SPA is potentially the largest impact crater in the Solar System (Stuart-Alexander, 1978), and covers most of the central southern farside (see Fig. 8.1). SPA is both topographically and compositionally distinct from the rest of the Moon, as well as potentially being the oldest identifiable structure on the surface (e.g., Jolliff et al., 2003). Determining the age of SPA was explicitly cited by the National Research Council (2007) as their second priority out of 35 goals. A major finding of our study is that nearly all science goals can be addressed within SPA. As the lunar south pole has many engineering advantages over other locations (e.g., areas with enhanced illumination and little temperature variation, hydrogen deposits), it has been proposed as a site for a future human lunar outpost. If this were to be the case, SPA would be the closest major geologic feature, and thus the primary target for long-distance traverses from the outpost. Clark et al. (2008) described four long traverses from the center of SPA going to Olivine Hill (Pieters et al., 2001), Oppenheimer Basin, Mare Ingenii, and Schrödinger Basin, with a stop at the South Pole. This chapter will identify other potential sites for future exploration across SPA, highlighting sites with both great scientific potential and proximity to the lunar South Pole. -

Florida Atlantic University
FLORIDA ATLANTIC UNIVERSITY Commencement Classes d196S -1969 Sunday, June 8, 1969 Two o'Clock THE CAMPUS Boca Raton, Florida !fJrogram Prelude Prelude and Fugue in C. Major- ]. S. Bach Processional Pomp and Circumstance- Edward Elgar B. Graham Ellerbee, Organist Introductions Dr. Clyde R. Burnett University Marshal Invocation The Rev. Donald Barrus United Campus Ministries National Anthem - Key- Sousa Richard Wright Instructor in Music Presiding Dr. Kenneth R. Williams President Florida Atlantic University Address "The Generation of City Builders" Dr. Robert C. Wood Director Joint Center for Urban Studies Massachusetts Institute of Technology Presentation of Baccalaureate Degrees Dr. S. E. Wimberly Vice President for Academic Affairs For the College of Business and Public Administration Dean Robert L. Froemke For the College of Education Dean Robert R. Wiegman For the College of Humanities Dean Jack Suberman For the Department of Ocean Engineering Professor Charles R. Stephan For the College of Science Dean Kenneth M. Michels For the College of Social Science Dean John M. DeGrove Presentation of the Master of Education, Master of Public Administration, Master of Science and Master of Arts Degrees Deans of the Respective Colleges Benediction The Reverend Barrus Recessional Recessional - Martin Shaw The Audience will please remain in their places until the Faculty and Graduates have left the area. 1 THE ORDER OF THE PROCE SS IO N The Marshal of the Colleges The Marshals and Candidates of the College of Business and Public Administration -
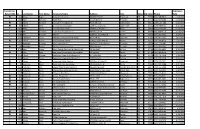
Installers.Pdf
Initial (I) or Expiration Recert (RI) Id Last Name First Sept Name Company Name Address City State Zip Code Phone Date RI 212 Abbas Roger Abbas Construction 6827 NE 33rd St Redmond OR 97756 (541) 548-6812 2/3/2024 I 2888 Adair Benjamin Septic Pros 1751 N Main st Prineville OR 97754 (541) 359-8466 5/10/2024 RI 727 Adams Kenneth Ken Adams Plumbing Inc 906 N 9th Ave Walla Walla WA 99362 (509) 529-7389 6/23/2023 RI 884 Adcock Dean Tri County Construction 22987 SE Dowty Rd Eagle Creek OR 97022 (503) 948-0491 9/25/2023 I 2592 Adelt Georg Cascade Valley Septic 17360 Star Thistle Ln Bend OR 97703 (541) 337-4145 11/18/2022 I 2994 Agee Jetamiah Leavn Trax Excavation LLC 50020 Collar Dr. La Pine OR 97739 (541) 640-3115 9/13/2024 I 2502 Aho Brennon BRX Inc 33887 SE Columbus St Albany OR 97322 (541) 953-7375 6/24/2022 I 2392 Albertson Adam Albertson Construction & Repair 907 N 6th St Lakeview OR 97630 (541) 417-1025 12/3/2021 RI 831 Albion Justin Poe's Backhoe Service 6590 SE Seven Mile Ln Albany OR 97322 (541) 401-8752 7/25/2022 I 2732 Alexander Brandon Blux Excavation LLC 10150 SE Golden Eagle Dr Prineville OR 97754 (541) 233-9682 9/21/2023 RI 144 Alexander Robert Red Hat Construction, Inc. 560 SW B Ave Corvallis OR 97333 (541) 753-2902 2/17/2024 I 2733 Allen Justan South County Concrete & Asphalt, LLC PO Box 2487 La Pine OR 97739 (541) 536-4624 9/21/2023 RI 74 Alley Dale Back Street Construction Corporation PO Box 350 Culver OR 97734 (541) 480-0516 2/17/2024 I 2449 Allison Michael Deschutes Property Solultions, LLC 15751 Park Dr La Pine OR 97739 (541) 241-4298 5/20/2022 I 2448 Allison Tisha Deschutes Property Solultions, LLC 15751 Park Dr La Pine OR 97739 (541) 241-4298 5/20/2022 RI 679 Alman Jay Integrated Water Services 4001 North Valley Dr. -

Origin of the Anomalously Rocky Appearance of Tsiolkovskiy Crater
Icarus 273 (2016) 237–247 Contents lists available at ScienceDirect Icarus journal homepage: www.elsevier.com/locate/icarus Origin of the anomalously rocky appearance of Tsiolkovskiy crater ∗ Benjamin T. Greenhagen a, , Catherine D. Neish b, Jean-Pierre Williams c, Joshua T.S. Cahill a, Rebecca R. Ghent d,e,PaulO. Hayne f, Samuel J. Lawrence g,NoahE. Petro h, Joshua L. Bandfield i a Johns Hopkins University Applied Physics Laboratory, 11100 Johns Hopkins Road, Laurel, MD 20723-6099, United States b Department of Earth Sciences, Western University Biological & Geological Sciences Building, Room 1026 1151 Richmond St. N. London, ON N6A 5B7 Canada c Department of Earth, Planetary, and Space Sciences, University of California, Los Angeles 595 Charles Young Drive East, Box 951567 Los Angeles, CA 90095-1567, United States d Department of Earth Sciences, Earth Sciences Centre 22 Russell Street Toronto, Ontario, M5S 3B1, Canada e Planetary Science Institute, 1700 East Fort Lowell, Suite 106 Tucson, AZ 85719-2395, United States f Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive Pasadena, CA 91109 ASU, United States g School of Earth and Space Exploration, PO Box 871404 Tempe, AZ 85287-1404, United States h NASA’s Goddard Space Flight Center, 8800 Greenbelt Rd Greenbelt, MD 20771, United States i Space Science Institute, 4750 Walnut Street | Suite 205 Boulder, Colorado 80301, United States a r t i c l e i n f o a b s t r a c t Article history: Rock abundance maps derived from the Diviner Lunar Radiometer instrument on the Lunar Reconnais- Received 3 August 2015 sance Orbiter (LRO) show Tsiolkovskiy crater to have high surface rock abundance and relatively low re- Revised 6 February 2016 golith thickness. -

Lunar Impact Basins Revealed by Gravity Recovery and Interior
Lunar impact basins revealed by Gravity Recovery and Interior Laboratory measurements Gregory Neumann, Maria Zuber, Mark Wieczorek, James Head, David Baker, Sean Solomon, David Smith, Frank Lemoine, Erwan Mazarico, Terence Sabaka, et al. To cite this version: Gregory Neumann, Maria Zuber, Mark Wieczorek, James Head, David Baker, et al.. Lunar im- pact basins revealed by Gravity Recovery and Interior Laboratory measurements. Science Advances , American Association for the Advancement of Science (AAAS), 2015, 1 (9), pp.e1500852. 10.1126/sci- adv.1500852. hal-02458613 HAL Id: hal-02458613 https://hal.archives-ouvertes.fr/hal-02458613 Submitted on 26 Jun 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. RESEARCH ARTICLE PLANETARY SCIENCE 2015 © The Authors, some rights reserved; exclusive licensee American Association for the Advancement of Science. Distributed Lunar impact basins revealed by Gravity under a Creative Commons Attribution NonCommercial License 4.0 (CC BY-NC). Recovery and Interior Laboratory measurements 10.1126/sciadv.1500852 Gregory A. Neumann,1* Maria T. Zuber,2 Mark A. Wieczorek,3 James W. Head,4 David M. H. Baker,4 Sean C. Solomon,5,6 David E. Smith,2 Frank G. -

Scattering Properties of Jackson Crater in the Lunar Far Side
43rd Lunar and Planetary Science Conference (2012) 1234.pdf SCATTERING PROPERTIES OF JACKSON CRATER IN THE LUNAR FAR SIDE. Sriram Saran, Anup Das, Shiv Mohan and Manab Chakraborty, Space Applications Centre (ISRO), Ahmedabad, India ([email protected]) Introduction: Large and fresh lunar craters are as quantitative estimates of surface roughness and sur- best targets to understand impact cratering, because face composition and are very useful for differentiating space weathering and subsequent small impacts are the independent geologic deposits [6]. Also, the decompo- 2 2 2 1/2 major processes that disturb the original structure of sition of m-δ (m= (S1 + S2 + S3 ) /S0 - degree of -1 ejecta units over time [1]. Analysis of morphology and polarization; δ=tan (-S3/S2) - relative phase between ejecta distribution of such fresh craters can give impor- two polarization channels) feature space [2] has been tant clues to reconstruct the impact event and pre- implemented in this study which provides the domi- impact sub surface structures. To illustrate this, scatter- nant scattering mechanism corresponding to a target or ing properties of Jackson crater (70 km-diameter), one within a radar resolution cell, expressed as of the most enigmatic features in the northern hemi- sphere of lunar far side, have been analysed in this R = S0 m(1 sin )/ 2 study. Bright rays streak for hundreds of kilometres across the lunar surface originate from Jackson crater, G = S0 (1 m) (2) which has a large forbidden zone in the NW sector suggesting that Jackson was formed by an oblique im- B = S0 m(1 sin )/ 2 pact along the NW-SE direction [1].