Decreased Frequency of Strong Bars in S0 Galaxies: Evidence For
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
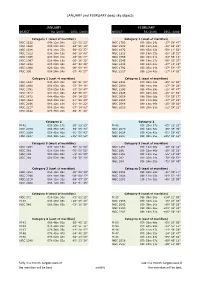
SPIRIT Target Lists
JANUARY and FEBRUARY deep sky objects JANUARY FEBRUARY OBJECT RA (2000) DECL (2000) OBJECT RA (2000) DECL (2000) Category 1 (west of meridian) Category 1 (west of meridian) NGC 1532 04h 12m 04s -32° 52' 23" NGC 1792 05h 05m 14s -37° 58' 47" NGC 1566 04h 20m 00s -54° 56' 18" NGC 1532 04h 12m 04s -32° 52' 23" NGC 1546 04h 14m 37s -56° 03' 37" NGC 1672 04h 45m 43s -59° 14' 52" NGC 1313 03h 18m 16s -66° 29' 43" NGC 1313 03h 18m 15s -66° 29' 51" NGC 1365 03h 33m 37s -36° 08' 27" NGC 1566 04h 20m 01s -54° 56' 14" NGC 1097 02h 46m 19s -30° 16' 32" NGC 1546 04h 14m 37s -56° 03' 37" NGC 1232 03h 09m 45s -20° 34' 45" NGC 1433 03h 42m 01s -47° 13' 19" NGC 1068 02h 42m 40s -00° 00' 48" NGC 1792 05h 05m 14s -37° 58' 47" NGC 300 00h 54m 54s -37° 40' 57" NGC 2217 06h 21m 40s -27° 14' 03" Category 1 (east of meridian) Category 1 (east of meridian) NGC 1637 04h 41m 28s -02° 51' 28" NGC 2442 07h 36m 24s -69° 31' 50" NGC 1808 05h 07m 42s -37° 30' 48" NGC 2280 06h 44m 49s -27° 38' 20" NGC 1792 05h 05m 14s -37° 58' 47" NGC 2292 06h 47m 39s -26° 44' 47" NGC 1617 04h 31m 40s -54° 36' 07" NGC 2325 07h 02m 40s -28° 41' 52" NGC 1672 04h 45m 43s -59° 14' 52" NGC 3059 09h 50m 08s -73° 55' 17" NGC 1964 05h 33m 22s -21° 56' 43" NGC 2559 08h 17m 06s -27° 27' 25" NGC 2196 06h 12m 10s -21° 48' 22" NGC 2566 08h 18m 46s -25° 30' 02" NGC 2217 06h 21m 40s -27° 14' 03" NGC 2613 08h 33m 23s -22° 58' 22" NGC 2442 07h 36m 20s -69° 31' 29" Category 2 Category 2 M 42 05h 35m 17s -05° 23' 25" M 42 05h 35m 17s -05° 23' 25" NGC 2070 05h 38m 38s -69° 05' 39" NGC 2070 05h 38m 38s -69° -

Nuclear Activity in Circumnuclear Ring Galaxies
International Journal of Astronomy and Astrophysics, 2016, 6, 219-235 Published Online September 2016 in SciRes. http://www.scirp.org/journal/ijaa http://dx.doi.org/10.4236/ijaa.2016.63018 Nuclear Activity in Circumnuclear Ring Galaxies María P. Agüero1, Rubén J. Díaz2,3, Horacio Dottori4 1Observatorio Astronómico de Córdoba, UNCand CONICET, Córdoba, Argentina 2ICATE, CONICET, San Juan, Argentina 3Gemini Observatory, La Serena, Chile 4Instituto de Física, UFRGS, Porto Alegre, Brazil Received 23 May 2016; accepted 26 July 2016; published 29 July 2016 Copyright © 2016 by authors and Scientific Research Publishing Inc. This work is licensed under the Creative Commons Attribution International License (CC BY). http://creativecommons.org/licenses/by/4.0/ Abstract We have analyzed the frequency and properties of the nuclear activity in a sample of galaxies with circumnuclear rings and spirals (CNRs), compiled from published data. From the properties of this sample a typical circumnuclear ring can be characterized as having a median radius of 0.7 kpc (mean 0.8 kpc, rms 0.4 kpc), located at a spiral Sa/Sb galaxy (75% of the hosts), with a bar (44% weak, 37% strong bars). The sample includes 73 emission line rings, 12 dust rings and 9 stellar rings. The sample was compared with a carefully matched control sample of galaxies with very similar global properties but without detected circumnuclear rings. We discuss the relevance of the results in regard to the AGN feeding processes and present the following results: 1) bright companion galaxies seem -

The Pendulum Clock Lum Clock Around the Hand Section Is Situated Around Iota, Eta and Zeta Horologii
deep-sky delights Eridanus to its The Pendulum north, Reticulum Clock diagonally east- ward, and Hydrus by Magda Streicher to the south. The [email protected] constellation was originally named Horologium “Time and tide wait for no man” – a Oscillitorium to Image source: Starry Night Pro proverb whose truth can be in no doubt. honour Christian Everything revolves around time, which Huygens, the is why it isn’t at all strange to see a con- famous Dutch stellation called “Horologium, the clock” scientist, inventor in the starry sky. of the pendulum in 1657 and the discov- erer of Saturn’s rings. Horologium is one Going back somewhat in time, Frikkie de of Nicolas-Louis de Lacaille’s (1713-62) Bruyn (Cosmology Director) has drawn fourteen constellations which he created our attention to the following: By the during his stay at the Cape of Good Hope end of the nineteenth century scientists from 1750 to 1752. It was with this visit believed in a universal quantity called that he established the framework for as- time which all clocks would measure. tronomy in South Africa. In my mind’s However, Albert Einstein’s theory of eye I clearly see the gentleman Lacaille relativity had overthrown two pillars of carrying his pocket watch with some the nineteenth-century science: absolute pride, elegantly attached to his jacket by rest, as represented by the idea of an all means of a gold chain (my imagination pervading ether and absolute or univer- again!). Time possibly stood still for sal time. Every person has his or her him too, so that he was able to explore own personal time. -

The Bennett Catalogue
The Bennett Catalogue www.macastro.org.au Catalogue Numbers Type R.A. Dec. U2000 Con. Ben 1 NGC 55 Gal 0:14:54 -39:11 386 Scl Ben 2 NGC 104 GC 0:24:06 -72:05 440 Tuc Ben 3 NGC 247 Gal 0:47:06 -20:46 306 Cet Ben 4 NGC 253 Gal 0:47:36 -25:17 306 Scl Ben 5 NGC 288 GC 0:52:48 -26:35 307 Scl Ben 6 NGC 300 Gal 0:54:54 -37:41 351 Scl Ben 7 NGC 362 GC 1:03:12 -70:51 441 Tuc Ben 8 NGC 613 Gal 1:34:18 -29:25 352 Scl Ben 9 NGC 1068 Gal 2:42:42 -00:01 220 Cet Ben 10 NGC 1097 Gal 2:46:18 -30:17 354 For Ben 10a NGC 1232 Gal 3:09:48 -20:35 311 Eri Ben 11 NGC 1261 GC 3:12:18 -55:13 419 Hor Ben 12 NGC 1291 Gal 3:17:18 -41:08 390 Eri Ben 13 NGC 1313 Gal 3:18:18 -66:30 443 Ret Ben 14 NGC 1316 Gal 3:22:42 -37:12 355 For Ben 14a NGC 1350 Gal 3:31:06 -33:38 355 For Ben 15 NGC 1360 PN 3:33:18 -25:51 312 For Ben 16 NGC 1365 Gal 3:33:36 -36:08 355 For Ben 17 NGC 1380 Gal 3:36:30 -34:59 355 For Ben 18 NGC 1387 Gal 3:37:00 -35:31 355 For Ben 19 NGC 1399 Gal 3:38:30 -35:27 355 For Ben 19a NGC 1398 Gal 3:38:54 -26:20 312 For Ben 20 NGC 1404 Gal 3:38:54 -35:35 355 Eri Ben 21 NGC 1433 Gal 3:42:00 -47:13 391 Hor Ben 21a NGC 1512 Gal 4:03:54 -43:21 391 Hor Ben 22 NGC 1535 PN 4:14:12 -12:44 268 Eri Ben 23 NGC 1549 Gal 4:15:42 -55:36 420 Dor Ben 24 NGC 1553 Gal 4:16:12 -55:47 420 Dor Ben 25 NGC 1566 Gal 4:20:00 -54:56 420 Dor Ben 25a NGC 1617 Gal 4:31:42 -54:36 421 Dor Ben 26 NGC 1672 Gal 4:45:42 -59:15 421 Dor Ben 27 NGC 1763 BN 4:56:48 -66:24 444 Dor Ben 28 NGC 1783 GC 4:58:54 -66:00 444 Dor Ben 29 NGC 1792 Gal 5:05:12 -37:59 358 Col -

Super-Massive Black Hole Scaling Relations and Peculiar Ringed Galaxies
SUPER-MASSIVE BLACK HOLE SCALING RELATIONS AND PECULIAR RINGED GALAXIES A DISSERTATION SUBMITTED TO THE FACULTY OF THE GRADUATE SCHOOL OF THE UNIVERSITY OF MINNESOTA BY BURCIN MUTLU IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY MARC S. SEIGAR June, 2017 c BURCIN MUTLU 2017 ALL RIGHTS RESERVED Acknowledgements There are several people who I would like to acknowledge for directly or indirectly contributing to this dissertation. First and foremost, I would like to acknowledge the guidance and support of my ad- visor, Marc S. Seigar. I am thankful to him for his continuous encouragement, patience, and kindness. I appreciate all his contributions of knowledge, expertise, and time, which were invaluable to my success in graduate school. He has set an example of excellence as a researcher, mentor, and role model. In addition, I would like to thank my dissertation committee, Liliya L. R. Williams, M. Claudia Scarlata, and Robert Lysak, for their insightful input, constructive criticism and direction during the course of this dissertation. I have crossed paths with many collaborators who have influenced and enhanced my research. Patrick Treuthardt has been a collaborator for most of the work during my dissertation. The addition of his scientific point of view has improved the quality of the work in this dissertation tremendously. Our discussions have always been stimulating and rewarding. I am thankful to him for mentoring me and being a dear friend to me. I would also like to thank Benjamin L. Davis for numerous helpful advice and inspiring discussions. He has directly involved with many aspects of Chapter 1. -

The Black Hole Mass Function Derived from Local Spiral Galaxies
PUBLISHED IN THE ASTROPHYSICAL JOURNAL, 789:124 (16PP),2014 JULY 10 Preprint typeset using LATEX style emulateapj v. 12/16/11 THE BLACK HOLE MASS FUNCTION DERIVED FROM LOCAL SPIRAL GALAXIES BENJAMIN L. DAVIS1 , JOEL C. BERRIER1,2,5,LUCAS JOHNS3,6 ,DOUGLAS W. SHIELDS1,2, MATTHEW T. HARTLEY2,DANIEL KENNEFICK1,2, JULIA KENNEFICK1,2, MARC S. SEIGAR1,4 , AND CLAUD H.S. LACY1,2 Published in The Astrophysical Journal, 789:124 (16pp), 2014 July 10 ABSTRACT We present our determination of the nuclear supermassive black hole mass (SMBH) function for spiral galax- ies in the local universe, established from a volume-limited sample consisting of a statistically complete col- lection of the brightest spiral galaxies in the southern (δ< 0◦) hemisphere. Our SMBH mass function agrees well at the high-mass end with previous values given in the literature. At the low-mass end, inconsistencies exist in previous works that still need to be resolved, but our work is more in line with expectations based on modeling of black hole evolution. This low-mass end of the spectrum is critical to our understanding of the mass function and evolution of black holes since the epoch of maximum quasar activity. A limiting luminos- ity (redshift-independent) distance, DL = 25.4 Mpc (z =0.00572) and a limiting absolute B-band magnitude, MB = −19.12 define the sample. These limits define a sample of 140 spiral galaxies, with 128 measurable pitch angles to establish the pitch angle distribution for this sample. This pitch angle distribution function may be useful in the study of the morphology of late-type galaxies. -

An Atlas of Calcium Triplet Spectra of Active Galaxies
Mon. Not. R. Astron. Soc. 359, 765–780 (2005) doi:10.1111/j.1365-2966.2005.08957.x An atlas of calcium triplet spectra of active galaxies , A. Garcia-Rissmann,1 L. R. Vega,1 2 N. V. Asari,1 R. Cid Fernandes,1 Downloaded from https://academic.oup.com/mnras/article/359/2/765/988769 by Secretaria General Adjunta de Informatica user on 01 December 2020 H. Schmitt,3,4 R. M. Gonz´alez Delgado5 and T. Storchi-Bergmann6 1Depto. de F´ısica – CFM – Universidade Federal de Santa Catarina, C.P. 476, 88040-900, Florianopolis,´ SC, Brazil 2Observatorio Astronomico´ de Cordoba,´ Laprida 854, 5000, Cordoba,´ Argentina 3Remote Sensing Division, Code 7210, Naval Research Laboratory, 4555 Overlook Avenue, SW, Washington, DC 20375, USA 4Interferometric Inc., 14 120 Parke Long Court, 103, Chantilly, VA 20151, USA 5Instituto de Astrof´ısica de Andaluc´ıa (CSIC), PO Box 3004, 18080 Granada, Spain 6Instituto de F´ısica, Universidade Federal do Rio Grande do Sul, C.P. 15001, 91501-970, Porto Alegre, RS, Brazil Accepted 2005 February 21. Received 2005 February 21; in original form 2004 December 24 ABSTRACT We present a spectroscopic atlas of active galactic nuclei covering the region around the λλ8498, 8542, 8662 calcium triplet (CaT). The sample comprises 78 objects, divided into 43 Seyfert 2s, 26 Seyfert 1s, three starburst and six normal galaxies. The spectra pertain to the inner ∼300 pc in radius, and thus sample the central kinematics and stellar populations of active galaxies. The data are used to measure stellar velocity dispersions (σ ) with both cross-correlation and direct fitting methods. -

TABLE 1 Explanation of CVRHS Symbols A
TABLE 1 Explanation of CVRHS Symbols a Symbol Description 1 2 General Terms ETG An early-type galaxy, collectively referring to a galaxy in the range of types E to Sa ITG An intermediate-type galaxy, taken to be in the range Sab to Sbc LTG A late-type galaxy, collectively referring to a galaxy in the range of types Sc to Im ETS An early-type spiral, taken to be in the range S0/a to Sa ITS An intermediate-type spiral, taken to be in the range Sab to Sbc LTS A late-type spiral, taken to be in the range Sc to Scd XLTS An extreme late-type spiral, taken to be in the range Sd to Sm classical bulge A galaxy bulge that likely formed from early mergers of smaller galaxies (Kormendy & Kennicutt 2004; Athanassoula 2005) pseudobulge A galaxy bulge made of disk material that has secularly collected into the central regions of a barred galaxy (Kormendy 2012) PDG A pure disk galaxy, a galaxy lacking a classical bulge and often also lacking a pseudobulge Stage stage The characteristic of galaxy morphology that recognizes development of structure, the widespread distribution of star formation, and the relative importance of a bulge component along a sequence that correlates well with basic characteristics such as integrated color, average surface brightness, and HI mass-to-blue luminosity ratio Elliptical Galaxies E galaxy A galaxy having a smoothly declining brightness distribution with little or no evidence of a disk component and no inflections (such as lenses) in the luminosity distribution (examples: NGC 1052, 3193, 4472) En An elliptical galaxy -

A Classical Morphological Analysis of Galaxies in the Spitzer Survey Of
Accepted for publication in the Astrophysical Journal Supplement Series A Preprint typeset using LTEX style emulateapj v. 03/07/07 A CLASSICAL MORPHOLOGICAL ANALYSIS OF GALAXIES IN THE SPITZER SURVEY OF STELLAR STRUCTURE IN GALAXIES (S4G) Ronald J. Buta1, Kartik Sheth2, E. Athanassoula3, A. Bosma3, Johan H. Knapen4,5, Eija Laurikainen6,7, Heikki Salo6, Debra Elmegreen8, Luis C. Ho9,10,11, Dennis Zaritsky12, Helene Courtois13,14, Joannah L. Hinz12, Juan-Carlos Munoz-Mateos˜ 2,15, Taehyun Kim2,15,16, Michael W. Regan17, Dimitri A. Gadotti15, Armando Gil de Paz18, Jarkko Laine6, Kar´ın Menendez-Delmestre´ 19, Sebastien´ Comeron´ 6,7, Santiago Erroz Ferrer4,5, Mark Seibert20, Trisha Mizusawa2,21, Benne Holwerda22, Barry F. Madore20 Accepted for publication in the Astrophysical Journal Supplement Series ABSTRACT The Spitzer Survey of Stellar Structure in Galaxies (S4G) is the largest available database of deep, homogeneous middle-infrared (mid-IR) images of galaxies of all types. The survey, which includes 2352 nearby galaxies, reveals galaxy morphology only minimally affected by interstellar extinction. This paper presents an atlas and classifications of S4G galaxies in the Comprehensive de Vaucouleurs revised Hubble-Sandage (CVRHS) system. The CVRHS system follows the precepts of classical de Vaucouleurs (1959) morphology, modified to include recognition of other features such as inner, outer, and nuclear lenses, nuclear rings, bars, and disks, spheroidal galaxies, X patterns and box/peanut structures, OLR subclass outer rings and pseudorings, bar ansae and barlenses, parallel sequence late-types, thick disks, and embedded disks in 3D early-type systems. We show that our CVRHS classifications are internally consistent, and that nearly half of the S4G sample consists of extreme late-type systems (mostly bulgeless, pure disk galaxies) in the range Scd-Im. -

ALABAMA University Libraries
THE UNIVERSITY OF ALABAMA University Libraries Ultraviolet Signposts of Resonant Dynamics in the Starbursts-Ringed Sab Galaxy M94 (NGC 4736) William C. Keel – University of Alabama et al. Deposited 09/17/2018 Citation of published version: Waller, William., et al. (2001): Ultraviolet Signposts of Resonant Dynamics in the Starbursts-Ringed Sab Galaxy M94 (NGC 4736). The Astronomical Journal, 121(3). DOI: 10.1086/319384 © 2001. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE ASTRONOMICAL JOURNAL, 121:1395È1412, 2001 March ( 2001. The American Astronomical Society. All rights reserved. Printed in U.S.A. ULTRAVIOLET SIGNPOSTS OF RESONANT DYNAMICS IN THE STARBURST-RINGED Sab GALAXY M94 (NGC 4736) WILLIAM H. WALLER,1,2 MICHAEL N. FANELLI,2,3 WILLIAM C. KEEL,4 RALPH BOHLIN,5 NICHOLAS R. COLLINS,2 BARRY F. MADORE,6 PAMELA M. MARCUM,7 SUSAN G. NEFF,8 ROBERT W. OÏCONNELL,9 JOEL D. OFFENBERG,2 MORTON S. ROBERTS,10 ANDREW M. SMITH,8 AND THEODORE P. STECHER8 Received 2000 May 11; accepted 2000 October 31 ABSTRACT The dynamic orchestration of star-birth activity in the starburst-ringed galaxy M94 (NGC 4736) is investigated using images from the Ultraviolet Imaging Telescope (UIT; far-ultraviolet [FUV] band), Hubble Space Telescope (HST ; near-ultraviolet [NUV] band), Kitt Peak 0.9 m telescope (Ha, R, and I bands), and Palomar 5 m telescope (B band), along with spectra from the International Ultraviolet Explorer (IUE) and the Lick 1 m telescope. The wide-Ðeld UIT image shows FUV emission from (1) an elongated nucleus, (2) a di†use inner disk, where Ha is observed in absorption, (3) a bright inner ring of H II regions at the perimeter of the inner disk (R \ 48A \ 1.1 kpc), and (4) two 500 pc size knots of hot stars exterior to the ring on diametrically opposite sides of the nucleus (R \ 130A \ 2.9 kpc). -

ALABAMA University Libraries
THE UNIVERSITY OF ALABAMA University Libraries The Distribution of Bar and Spiral Arm Strengths in Disk Galaxies R. Buta – University of Alabama S. Vasylyev – University of Alabama H. Salo – University of Oulu, Finland E. Laurikainen – University of Oulu, Finland Deposited 06/13/2018 Citation of published version: Buta, R., Vasylyev, S., Salo, H., Laurikainen, E. (2005): The Distribution of Bar and Spiral Arm Strengths in Disk Galaxies. The Astronomical Journal, 130(2). DOI: 10.1086/431251 © 2005. The American Astronomical Society. All rights reserved. Printed in U.S.A. The Astronomical Journal, 130:506 –523, 2005 August A # 2005. The American Astronomical Society. All rights reserved. Printed in U.S.A. THE DISTRIBUTION OF BAR AND SPIRAL ARM STRENGTHS IN DISK GALAXIES R. Buta and S. Vasylyev Department of Physics and Astronomy, University of Alabama, Box 870324, Tuscaloosa, AL 35487 and H. Salo and E. Laurikainen Division of Astronomy, Department of Physical Sciences, University of Oulu, Oulu FIN-90014, Finland Received 2005 March 11; accepted 2005 April 18 ABSTRACT The distribution of bar strengths in disk galaxies is a fundamental property of the galaxy population that has only begun to be explored. We have applied the bar-spiral separation method of Buta and coworkers to derive the distribution of maximum relative gravitational bar torques, Qb, for 147 spiral galaxies in the statistically well- defined Ohio State University Bright Galaxy Survey (OSUBGS) sample. Our goal is to examine the properties of bars as independently as possible of their associated spirals. We find that the distribution of bar strength declines smoothly with increasing Qb, with more than 40% of the sample having Qb 0:1. -

AINUR: Atlas of Images of Nuclear Rings 3 Dust but Have the Size of Star-Forming Nuclear Rings
Mon. Not. R. Astron. Soc. 000, 1–32 (2009) Printed 1 November 2018 (MN LATEX style file v2.2) AINUR: Atlas of Images of NUclear Rings S. Comeron´ 1⋆, J. H. Knapen1,2, J. E. Beckman1,2,3, E. Laurikainen4, H. Salo4, I. Mart´ınez-Valpuesta1,2, and R. J. Buta5 1Instituto de Astrof´ısica de Canarias, E-38200 La Laguna, Tenerife, Spain 2Departamento de Astrof´ısica, Universidad de La Laguna, E-38205 La Laguna, Tenerife, Spain 3Consejo Superior de Investigaciones Cient´ıficas, Spain 4Division of Astronomy, Department of Physical Sciences, University of Oulu, Oulu FIN-90014, Finland 5Department of Physics and Astronomy, University of Alabama, Tuscaloosa, AL 35847, USA Accepted. Received; in original form ABSTRACT We present the most complete atlas of nuclear rings to date. We include 113 rings found in 107 galaxies, six of which are elliptical galaxies, five are highly inclined disc galaxies, 18 are unbarred disc galaxies, and 78 are barred disc galaxies. Star-forming nuclear rings occur in 20±2% of disc galaxies with types between T = −3 and T = 7. We aim to explore possible relationships between the size and morphology of the rings and various galactic parameters. We also aim to establish whether ultra-compact nuclear rings are a distinct population of nuclear rings or if they are merely the low-end tail of the nuclear ring size distribution. We producecolour index and structure maps, as well as Hα and Paα continuum-subtracted images from HubbleS paceTelescope archival data. We derive ellipticity profiles from H-band Two- Micron All-Sky Srrvey images in order to detect bars and find their metric parameters.